Cilia perform various functions, including sensing, locomotion, generation of fluid flows and mass transport, serving to underpin a vast range of biological and ecological processes. However, analysis of the mass transport typically fails to resolve the near-field dynamics around individual cilia, and therefore overlooks the intricate role of power/recovery strokes of ciliary motion. Selvan et al. (2023, Phys. Rev. Fluids 8, 123103) observed that the flow field due to a point torque (i.e. a rotlet) accurately resolves both the near- and far-field characteristics of a single cilium’s flow in a semi-infinite domain. In this paper, we calculate the mass transport between a no-slip boundary and an adjacent fluid, as a model system for nutrient exchange with ciliated tissues. We develop a Langevin model in the presence of a point torque (i.e. a single cilium) to examine the nutrient flux from a localised surface source. This microscopic transport model is validated using a macroscopic continuum model, which directly solves the advection–diffusion equation. Our findings reveal that the flow induced by a point torque can enhance the particles’ transport, depending on their diffusivity and the magnitude of the point torque. Additionally, the average mass transport affected by a single cilium can be enhanced or diminished by the presence of an externally imposed linear shear flow, with a strong dependence on the alignment of the cilium. Taken together, this framework serves as a useful minimal model for examining the average nutrient exchange between ciliated tissues and fluid environments.

Particle image velocimetry is used to study the control of swirl momentum, delivered through an orifice formed by a physically rotating tube of finite length, relevant to the evolution of vortex rings produced at a Reynolds number ${Re}\approx 1000$ based on the average discharge velocity, for swirl numbers ${S} \in [0, 1]$. Experiments without discharge, reinforced with complimentary numerical predictions, reveal the presence of an intriguing secondary flow pattern in the rotating tube, preventing attainment of a solid-body-like swirl distribution. Nevertheless, it is found that fully established rings produced in this way, following discharge once conditions in the tube have reached a steady state, exhibit similar characteristics to rings formed by an otherwise solid-body rotating initial condition as explored computationally by Ortega-Chavez et al. (2023, J. Fluid Mech. 967, A16). Namely, opposite-signed vorticity forms due to vortex tilting, which subsequently interacts with the ring, promoting vorticity cancellation and vortex ring breakdown. A key feature of the experimental work is that partially established vortex rings, produced before a steady-state rotating tube condition is reached, show unique characteristics. Their creation, a short time after the onset of tube rotation: (i) facilitates more efficient delivery of swirl momentum to the vortex core area; (ii) maintains a low level of swirl in the ring bubble’s central region which would otherwise promote the formation of opposite-signed vorticity and vortex breakdown.

Three-dimensional eddy-resolving simulations are used to study the structure of turbulent boundary layers developing in an open channel where an array of sparse roughness elements in the form of partially burrowed mussels is placed on the smooth, flat channel bed starting at a certain streamwise location. The identical mussels are oriented with their major axis parallel to the mean flow. Their positions are randomised while making sure that the mussels are close to uniformly distributed inside the array. The turbulent flow approaching the leading edge of the array is fully developed. The protruding parts of the mussels play the role of sparse roughness elements and generate a rough-bed, internal boundary that is characterised by zero net flow exchange but non-zero local flow exchange due to active filtering. A double-averaging technique is used to obtain an equivalent, width- and time-averaged, boundary layer over a ‘flat’ rough surface containing no mussels. The paper discusses the effects of varying the mussel array density, protruding height of the mussels and filtering discharge on the spatial growth of the two-dimensional boundary layer. With proper scaling, the profiles of the (double-averaged) streamwise velocity are close to self-similar inside the inertial layer (e.g. for h $\lt$ z $\lt$ $\delta$, where h is the height of the protruding part of the mussels and $\delta$ is the boundary layer thickness) starting some distance from the leading edge of the array. The scaled turbulent kinetic energy and concentration profiles associated with the scalar advected through the excurrent syphons are also found to be self-similar above the vertical location where the maximum value is reached. An analytical model containing three subzones is proposed for the streamwise velocity in between the bed (z $=$ 0) and z $=$ $\delta$. The velocity profile inside the inertial region contains a law-of-the-wall component supplemented by a law-of-the-wake component. The scaling coefficient of the law-of-the-wake component is found to be larger than typical values used to describe velocity variation in turbulent boundary layers developing in a surrounding flow with close-to-uniform free stream velocity. The equivalent roughness height for this particular type of boundary layers developing over sparse roughness elements increases monotonically with h and the mussel array density, $\rho$N. The paper also discusses the effect of the mussel bed density on the average refiltration fraction and the phytoplankton removal efficiency of the mussel bed.

The Liebau effect generates a net flow without the need for valves. For the Liebau effect pumping phenomenon to occur, the pump must have specific characteristics. It needs tubes with different elastic properties and an actuator to provide energy to the fluid. The actuator periodically compresses the more flexible element. Furthermore, asymmetry is a crucial factor that differentiates between two pumping mechanisms: impedance pumping and asymmetric pumping. In this work, a model based on the fluid dynamics of an asymmetric valveless pump under resonant conditions is proposed to determine which parameters influence the pumped flow rate. Experimental work is used to validate the model, after which each of the parameters involved in the pump performance is dimensionlessly analysed. This highlights the most significant parameters influencing the pump performance such as the actuator period, length tube ratio and tube diameters. The results point out ways to increase a valveless asymmetric pump’s net-propelled flow rate, which has exciting applications in fields such as biomedicine. The model also allows for predicting the resonance period, a fundamental operating parameter for asymmetric pumping.

The dynamics of small-scale structures in free-surface turbulence is crucial to large-scale phenomena in natural and industrial environments. Here, we conduct experiments on the quasi-flat free surface of a zero-mean-flow turbulent water tank over the Reynolds number range $Re_{\lambda } = 207$–312. By seeding microscopic floating particles at high concentrations, the fine scales of the flow and the velocity-gradient tensor are resolved. A kinematic relation is derived expressing the contribution of surface divergence and vorticity to the dissipation rate. The probability density functions of divergence, vorticity and strain rate collapse once normalised by the Kolmogorov scales. Their magnitude displays strong intermittency and follows chi-square distributions with power-law tails at small values. The topology of high-intensity events and two-point statistics indicate that the surface divergence is characterised by dissipative spatial and temporal scales, while the high-vorticity and high-strain-rate regions are larger, long-lived, concurrent and elongated. The second-order velocity structure functions obey the classic Kolmogorov scaling in the inertial range when the dissipation rate on the surface is considered, with a different numerical constant than in three-dimensional turbulence. The cross-correlation among divergence, vorticity and strain rate indicates that the surface-attached vortices are strengthened during downwellings and diffuse when those dissipate. Sources (sinks) in the surface velocity fields are associated with strong (weak) surface-parallel stretching and compression along perpendicular directions. The floating particles cluster over spatial and temporal scales larger than those of the sinks. These results demonstrate that, compared with three-dimensional turbulence, in free-surface turbulence the energetic scales leave a stronger imprint on the small-scale quantities.

Elastoinertial turbulence (EIT) is a chaotic state that emerges in the flows of dilute polymer solutions. Direct numerical simulation (DNS) of EIT is highly computationally expensive due to the need to resolve the multiscale nature of the system. While DNS of two-dimensional (2-D) EIT typically requires $O(10^6)$ degrees of freedom, we demonstrate here that a data-driven modelling framework allows for the construction of an accurate model with 50 degrees of freedom. We achieve a low-dimensional representation of the full state by first applying a viscoelastic variant of proper orthogonal decomposition to DNS results, and then using an autoencoder. The dynamics of this low-dimensional representation is learned using the neural ordinary differential equation (NODE) method, which approximates the vector field for the reduced dynamics as a neural network. The resulting low-dimensional data-driven model effectively captures short-time dynamics over the span of one correlation time, as well as long-time dynamics, particularly the self-similar, nested travelling wave structure of 2-D EIT in the parameter range considered.

We review some of the processes leading to dispersion and mixing in porous media, exploring the differences between the travel time distribution of fluid particles within a pore throat and between pore throats of different size within the porous layer. A recent paper of Liu et al. has combined a model of these travel time distributions with a continuous time random walk to quantify the dispersion as a function of the Peclet number. We describe some further problems relating to dispersive mixing of tracer which may be amenable to this approach, including dispersion caused by macroscopic lenses of different permeability, dispersion of tracer which partitions between the fluid and matrix and the effects of buoyancy on mixing.

We derive leading-order governing equations and boundary conditions for a sheet of viscous fluid retracting freely under surface tension. We show that small thickness perturbations about a flat base state can lead to regions of compression, where one or both of the principal tensions in the sheet becomes negative, and thus drive transient buckling of the sheet centre-surface. The general theory is applied to the simple model problem of a retracting viscous disc with small axisymmetric thickness variations. Transient growth in the centre-surface is found to be possible generically, with the dominant mode selected depending on the imposed initial thickness and centre-surface perturbations. An asymptotic reduction of the boundary conditions at the edge of the disc, valid in the limit of large normalised thickness perturbations, reduces the centre-surface evolution equation to an ordinary differentional equation (ODE) eigenvalue problem. Analysis of this eigenvalue problem leads to insights such as how the degree of transient buckling depends on the imposed thickness perturbation and which thickness perturbation gives rise to the largest transient buckling.

We investigate viscous dissipation in linear flows driven by small-amplitude longitudinal librations in rotating fluid spheres focusing on the rapid rotation regime applicable to planets. Viscous coupling can resonate with inertial modes in the bulk of the fluid when the frequency of the forcing is within the range $(0,2\Omega _0)$, where $\Omega _0$ is the mean angular velocity of the sphere. We solve the linearised equations of motion with a semi-spectral numerical method and with an asymptotic expansion exploiting the small Ekman number, $E$, which quantifies the strength of viscous forces relative to the Coriolis force. Our results confirm that the dominant contribution to the dissipation occurs in the Ekman boundary layer with leading-order scaling $E^{1/2}$. When the forcing frequency coincides with that of an inertial mode, dissipation is reduced by as much as 9 % compared with boundary layer theory alone. The percentage-wise reduction is independent of $E$ and the frequency width of the reduction envelope scales as $E^{1/2}$. At non-resonant frequencies conic shear layers develop in the bulk interior and, together with the Ekman layer bulge at critical latitude, slightly enhance dissipation. We confirm critical latitude bulge and shear layer contributions to the overall dissipation scale as $E^{4/5}$ and $E^{6/5}$ respectively, becoming negligible compared with dissipation in the main boundary layer as $E\rightarrow 0$. The frequencies at which the dissipation enhancement from critical latitude effects is maximised are displaced from the inviscid limit periodic orbit frequencies by a factor that scales with $E^{0.23}$.

The intrinsic uncertainty of fluid properties, including the equation-of-state, viscosity and thermal conductivity, on boundary layer stability has scarcely been addressed. When a fluid is operating in the vicinity of the Widom line (defined as the maximum of isobaric specific heat) in supercritical state, its properties exhibit highly non-ideal behavior, which is an ongoing research field leading to refined and more accurate fluid property databases. Upon crossing the Widom line, new mechanisms of flow instability emerge, feasibly leading to changes in dominating modes that yield turbulence. The present work investigates the sensitivity of three-dimensional boundary layer modal instability to these intrinsic uncertainties in fluid properties. The uncertainty, regardless of its source and the fluid regimes, gives rise to distortions of all profiles that constitute the inputs of the stability operator. The effect of these distortions on flow stability is measured by sensitivity coefficients, which are formulated with the adjoint operator and validated against linear modal stability analysis. The results are presented for carbon dioxide at a representative supercritical pressure of approximately 80 bar. The sensitivity to different inputs of the stability operator across various thermodynamic regimes shows an immense range of sensitivity amplitude. A balancing relationship between the density gradient and its perturbation leads to a quadratic effect across the Widom line, provoking significant sensitivity to distortions of the second derivative of the pressure with respect to the density, $\partial ^2 p/\partial \rho ^2$. From an application-oriented point of view, one important question is whether the correct baseflow profiles can be meaningfully analysed by the simplified ideal-fluid model. The integrated modal disturbance growth – the N factor calculated with different partly idealised models – indicates that the answer depends strongly on the thermodynamic regime investigated.

We consider the flow of a volume 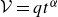$\mathcal {V} = q t^\alpha$ of viscous fluid injected into a gap 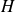$H$ between two horizontal plates (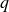$q$ and 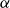$\alpha$ are positive constants, 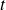$t$ is time). When the viscosity of the displaced fluid is negligible, the injected fluid forms a slug in contact with both plates connected (at a moving grounding line) to a gravity current (GC) with a downward-inclined interface. Hutchinson et al. (J. Fluid Mech., 598, 2023, pp. A4–1–13) considered a constant source (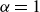$\alpha = 1$) of Newtonian fluid at the center of an axisymmetric gap; the flow, governed by the parameter 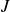$J$ (the height ratio of the unconfined GC to 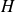$H$), admits a similarity solution. Here, the self-similar flow theory is (a) extended to rectangular geometry and power-law fluids, and (b) simplified. Similarity appears when 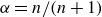$\alpha = n/(n+1)$ (two-dimensional) and 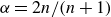$\alpha = 2n/(n+1)$ (axisymmetric), with propagation 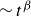$\sim t^\beta$, where 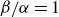$\beta /\alpha = 1$ and 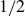$1/2$, respectively, and 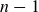$n-1$ is the power of the shear in the viscosity law (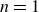$n=1$ for Newtonian fluid). The flow is governed by a single parameter 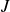$J$, representing the above-mentioned ratio. For small 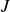$J$, the GC is mostly unconfined; for large 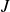$J$, almost all the injected fluid is in contact with both boundaries of the gap. For given geometry and $n$, we solve one ordinary differential equation (ODE) for the reduced thickness over the reduced length 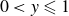$0\lt y \leqslant 1$, with a singular-regular condition at 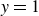$y=1$. The details of the confined GC, functions of 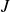$J$, follow by simple formulae.

The present study aims to provide an understanding of the influence of an afterbody on the flow-induced vibration (FIV) of cylinders. This is achieved through experimental and numerical investigations into the FIV response of a reverse-D-cross-section cylinder of aspect ratio $AR=5$. By carefully monitoring the point of flow separation to show it always occurs at the sharp top and bottom edges and never further upstream, it is demonstrated that vortex-induced vibration (VIV) can occur without an afterbody. However, for other aspect ratios, an afterbody does play a crucial role in determining the type of fluid forces responsible for sustaining VIV from low to moderate Reynolds numbers in the range $100$–$4700$. For a cylinder without an afterbody, it is found that the viscous force originating from the presence of strong compact vortices forming close to the leeward side of the cylinder is responsible for sustaining strong transverse vibration. In contrast, for a cylinder with an afterbody, the dominant force component depends on the size of the afterbody. In cylinders with a small afterbody, such as a reverse-D semi-circular cylinder, the viscous force dominates, while in cylinders with a larger afterbody such as a circular cylinder, the pressure force dominates.

We find the optimally time-dependent (OTD) orthogonal modes about a time-varying flow generated by a strong gust vortex impacting a NACA 0012 airfoil. This OTD analysis reveals the amplification characteristics of perturbations about the unsteady base flow and their amplified spatiotemporal structures that evolve over time. We consider four time-varying laminar base flows in which a vortex with a strength corresponding to the gust ratio $G$ of $\{-1,-0.5,0.5,1\}$ impinges on the leading edge of the airfoil at an angle of attack of $12^\circ$. In these cases, the impingement of the strong gust vortex causes massive separation and the generation of large-scale vortices around the airfoil within two convective time units. As these flow structures develop around the airfoil on a short time scale, the airfoil experiences large transient vortical lift variations in the positive and negative directions that are approximately five to ten times larger than the baseline lift. The highly unsteady nature of these vortex–airfoil interactions necessitates an advanced analytical technique capable of capturing the transient perturbation dynamics. For each of the considered gust ratios, the OTD analysis identifies the most amplified region to perturbations, the location of which changes as the wake evolves differently. For interactions between a moderate positive vortex gust ($G=0.5$) and the airfoil, the area where perturbations are amplified transitions from the leading-edge vortex (LEV) sheet to the forming LEV. Later, this most amplified structure becomes supported in the airfoil wake directly behind the trailing edge. In contrast, a strong vortex gust ($G=\pm 1$) encountered by the airfoil shows the most amplified OTD mode to appear around the core of the shed vortices. This study provides an analysis technique and fundamental insights into the broader family of unsteady aerodynamic problems.

Explaining fast magnetic reconnection in electrically conducting plasmas has been a theoretical challenge in plasma physics since its first description by Eugene N. Parker. In recent years, the observed reconnection rate has been shown by numerical simulations to be explained by the plasmoid instability that appears in highly conductive plasmas. In this work, by studying numerically the Orszag–Tang vortex, we show that the plasmoid instability is very sensitive to the numerical resolution used. It is shown that well-resolved runs display no plasmoid instability even at Lundquist numbers as large as $5\times 10^5$ achieved at resolutions of $32\,768^2$ grid points. On the contrary, in simulations that are under-resolved below a threshold, the plasmoid instability manifests itself with the formation of larger plasmoids the larger the under-resolving is. The present results thus emphasize the importance of performing convergence tests in numerical simulations and suggest that further investigations on the nonlinear evolution of the plasmoid instability are required.

Direct numerical simulations in periodic plane channels are used to study turbulent flow over ‘patches’ of roughness distributed on otherwise smooth walls. Circular patches as well as those resembling natural bio-fouling roughness are considered. Roughnesses within the patches are statistically similar and formed by random distribution of roughness elements of truncated cone shape. The two main studied parameters are the characteristic length scale of the patches $\varLambda _P$ and roughness area coverage ratio (CR). To provide a reference, simulations of homogeneous roughness (i.e. with 100 % CR) are performed at different roughness element densities translated into different values of frontal solidity. Results show that when $\varLambda _P$ is of the order of channel half-height $\delta$, the global friction coefficient $C_f$ of patchy roughness is scattered around that of homogeneous roughness with similar ‘mean’ frontal solidity. As $\varLambda _P/\delta$ grows, asymptotic convergence towards an equilibrium value is identified. Considering the present data, a normalised $C_f$ can be satisfactorily correlated by $\varLambda _P/\delta$; the normalisation includes $C_f$ for a homogeneous roughness similar to the patch roughness at two limiting cases. This points towards the possibility to develop a universal heterogeneous roughness correlation based on a knowledge of existing homogeneous roughness correlations. Furthermore, local and global flow statistics are studied, which among others, indicate formation of secondary motions for regular patch arrangement at $\varLambda _P\approx \delta$ with implications on the outer layer similarity of global mean velocity and Reynolds stress profiles.

The flow-induced oscillation of a transversely clamped buckled flexible filament in a uniform flow was explored using the penalty immersed boundary method. Both inverted and conventional configurations were analysed. The effects of bending rigidity, filament length and Reynolds number were examined. As these parameters were varied, four distinct modes were identified: conventional transverse oscillation mode, deflected oscillation mode, inverted transverse oscillation mode and structurally steady mode. The filament exhibited a 2S wake pattern under the conventional transverse oscillation mode and the small-amplitude inverted transverse oscillation mode, a P wake pattern under the deflected oscillation mode and a 2S + 2P wake pattern for the large-amplitude inverted transverse oscillation mode. Irrespective of their initial conditions, all of the filaments converged to the conventional transverse oscillation mode under low bending rigidity. Multistability was observed in the transversely clamped buckled flexible filament under moderate bending rigidity. The deflection in the oscillation mode increased with increasing filament length. The inverted buckled filament was sensitive to the Reynolds number, unlike the conventional buckled filament. The transverse oscillation mode demonstrated superior energy-harvesting performance.

We present a novel technique to render objects invisible to incident waves in a water waveguide system with parallel walls at low frequencies. The invisibility of a waveguide defect, specifically a vertical surface-piercing circular cylinder, is achieved through local deformations of the waveguide walls in the immediate vicinity of the defect. Our method results in a reflection coefficient that is at least 20 times lower than in the case of a parallel waveguide. The effect is observed over a broad frequency range. Experimental results confirm the high efficiency of our approach, showing that backscattered energy is reduced by a factor of 100–5000 compared with the reference case within the considered frequency range.

We consider the stability of Couette flow when travelling vibrations perturb one boundary. It is demonstrated that if the bounding surface profile takes the form of sinusoidal waves, then the otherwise stable shear flow becomes unstable for appropriately chosen values of vibration amplitude, phase speed and wavenumber. When instability arises, it is driven by centrifugal forces that are created by wave-imposed changes in the direction of fluid movement. Only subcritical waves, defined as vibrations with phase speed smaller than the maximum flow velocity, cause instability. As the fluid Reynolds number grows, the interval of vibration wavenumbers and phase speeds capable of flow destabilisation is enhanced. A range of parameters is identified for which the vibrations seem to play dual roles: they decrease the flow resistance while simultaneously generating streamwise vortices. This vibration class constitutes an energy-efficient control tool that may potentially intensify the mixing within a flow.

In this article, we investigate the behaviour of a cohesive granular material in a rotating drum. We use a model material with tuneable cohesion and vary the dimension of the drum in the radial and axial directions. The results show that the geometry of the drum may play a crucial role in the material dynamics, leading to significant changes in the surface morphology and flow regime. We attribute this behaviour to the fact that an increase in cohesion causes the grains to feel the sidewalls at a greater distance. Finally, we rationalize the results by introducing two dimensionless characteristic lengths, defined as the ratio of the drum dimensions to a cohesive length, which allow for the interpretation of the variation in the surface morphology and of the different flow regimes observed experimentally.

The impact of intrinsic compressibility effects – changes in fluid volume due to pressure variations – on high-speed wall-bounded turbulence has often been overlooked or incorrectly attributed to mean property variations. To quantify these intrinsic compressibility effects unambiguously, we perform direct numerical simulations of compressible turbulent channel flows with nearly uniform mean properties. Our simulations reveal that intrinsic compressibility effects yield a significant upward shift in the logarithmic mean velocity profile that can be attributed to the reduction in the turbulent shear stress. This reduction stems from the weakening of the near-wall quasi-streamwise vortices. In turn, we attribute this weakening to the spontaneous opposition of sweeps and ejections from the near-wall expansions and contractions of the fluid, and provide a theoretical explanation for this mechanism. Our results also demonstrate that intrinsic compressibility effects play a crucial role in the increase in inner-scaled streamwise turbulence intensity in compressible flows, as compared with incompressible flows, which was previously regarded to be an effect of mean property variations alone.