When turbulent convection interacts with a turbulent shear flow, the cores of convective cells become aligned with the mean current, and these cells (which span the height of the domain) may interact with motions closer to the solid boundary. In this work, we use coupled Eulerian–Lagrangian direct numerical simulations of a turbulent channel flow to demonstrate that, under conditions of turbulent mixed convection, interactions between motions associated with ejections and low-speed streaks near the solid boundary and coherent superstructures in the interior of the flow interact and lead to significant vertical transport of strongly settling Lagrangian particles. We show that the primary suspension mechanism is associated with strong ejection events (canonical low-speed streaks and hairpin vortices characterised by $u'\lt 0$ and $w'\gt 0$, where $u'$ and $w'$ are the streamwise and vertical turbulent velocity fluctuations), whereas secondary suspension is strongly associated with large-scale plume structures aligned with the mean shear (characterised by $w'\gt 0$ and $\theta '\gt 0$, where $\theta$ represents temperature fluctuations). This coupling, which is absent in the limiting cases (pure channel flow or free convection) is shown to lead to a sudden increase in the interior concentration profiles as ${Ri}_\tau$, the friction Richardson number, increases, resulting in concentrations that are larger by roughly an order of magnitude at the channel midplane.

Wave impact on solid structures is a well-studied phenomenon, but almost exclusively for the case that the impacting liquid (e.g. water) is surrounded by a non-condensable gas (such as air). In this study we turn to wave impact in a boiling liquid, a liquid that is in thermal equilibrium with its own vapour, which is of key relevance to the transport of cryogenic liquids, such as liquified natural gas and liquid hydrogen in the near future. More specifically, we use the Atmosphere facility at MARIN, NL, to prepare water/water vapour systems at different temperatures along the vapour curve. Here, we perform wave impact experiments by generating a soliton in a flume contained within the autoclave of the facility. A bathymetry profile interacts with the soliton, leading to a breaking wave that impacts onto a vertical wall, where we measure the pressures occurring during impact by means of $100$ embedded pressure sensors. In boiling liquids, we report wave impact pressures that are up to two orders of magnitude larger than those measured in comparable water–air experiments. We trace these pressures back to the collapse of the entrapped vapour pocket, which we semi-quantitatively describe using a simplified hemicylindrical vapour bubble model, which is in good agreement with the experimental findings. Finally, this allows us to predict the relevance of our findings for the transport of cryogenic liquids in huge overseas carriers where wave impact due to sloshing is the dominant cause of hydrodynamic load of containment systems in cargo tanks.

Surface gravity waves induce a drift on objects floating on the water’s surface. This study presents laboratory experiments investigating the drift of large two-dimensional floating objects on deep-water, unidirectional, regular waves, with wave steepness ranging from 0.04 to 0.31 (0.04 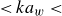$\lt k{a_w}\lt$ 0.31, where 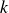$k$ is the wavenumber and 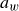$a_w$ the wave amplitude). The objects were carefully designed to have a rectangular cross-section with a constant aspect ratio; their size varied from 2.6 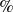$\%$ to 27 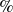$\%$ of the incident wavelength. We observed Lagrangian behaviour for small objects. Small and large objects exhibited fundamentally different drift behaviour at high compared with low wave steepness, with a regime shift observed at a certain size and wave steepness. The scaling of object drift with steepness depends on the relative size of the object. For small objects, drift scales with steepness squared, whereas drift becomes a linear function of steepness as the object size increases. For objects that are relatively large but smaller than 13–16% of a wavelength (low to high steepness), we provide experimental evidence supporting the mechanisms of drift enhancement recently identified by Xiao et al. (J. Fluid Mech., vol. 980, 2024, p. A27) and termed the ‘diffraction-modified Stokes drift’. This enhanced drift behaviour, compared with the theoretical Stokes drift for infinitely small fluid parcels, is attributed to changes in the objects’ oscillatory motion and local wave amplitude distribution (standing wave pattern) due to the presence of the object. In the case of larger objects, similar to Harms (J. Waterw. Port Coast. Ocean Eng., vol. 113(6), 1987, pp. 606–622), we relate the critical size at which drift is maximised to their vertical bobbing motion. We determine the domain of validity for both Stokes drift and the diffraction-modified Stokes drift model of Xiao et al. (J. Fluid Mech., vol. 980, 2024, A27) in terms of relative size and wave steepness and propose an empirical parametrisation based on our experimental data.

An important parameter characterising the synchronisation of turbulent flows is the threshold coupling wavenumber. This study investigates the relationship between the threshold coupling wavenumber and the leading Lyapunov vector using large eddy simulations and the SABRA model. Various subgrid-scale stress models, Reynolds numbers and different coupling methods are examined. A new scaling relation is identified for the leading Lyapunov exponents in large eddy simulations, showing that they approximate those of filtered direct numerical simulations. This interpretation provides a physical basis for results related to the Lyapunov exponents of large eddy simulations, including those related to synchronisation. Synchronisation experiments show that the peak wavenumber of the energy spectrum of the leading Lyapunov vector coincides with the threshold coupling wavenumber, in large eddy simulations of box turbulence with standard Smagorinsky or dynamic mixed models as well as in the SABRA model, replicating results from direct numerical simulations of box turbulence. Although the dynamic Smagorinsky model exhibits different behaviour, the totality of the results suggests that the relationship is an intrinsic property of a certain class of chaotic systems. We also confirm that conditional Lyapunov exponents characterise the synchronisation process in indirectly coupled systems as they do in directly coupled ones, with their values insensitive to the nature of the master flow. These findings advance the understanding of the role of the Lyapunov vector in the synchronisation of turbulence.

Three-dimensional wake forcing is applied to a profiled blunt trailing edge body from synthetic jet arrays distributed symmetrically on both sides of the body. The effect on the wake is experimentally studied at Reynolds numbers based on body thickness, $d$, of $2500 \leqslant Re_d=u_\infty d/\nu \leqslant 5000$ in the turbulent wake regime. The exits of the synthetic jets are rectangular slots and are oriented spanwise to the cross-flow with a uniform spacing of $2.4d$. The forcing causes spanwise variations in the separated shear layers, leading to the von Kármán vortices tilting and forming coherent streamwise vortex loops. This reorientation of the wake vorticity is associated with the attenuation of the vortex street and drag reduction, consistent with previous studies of spanwise perturbations to wakes. The effect of forcing amplitude on the drag and wake structure is examined. It is found that the mean shedding frequency is constant across the span in all cases, indicating that the forced wake has a periodic organised structure. The greatest drag reduction of approximately 25 % is achieved when the vortical structures emitted by the jets penetrate up the edges of the boundary layers of the body, which occurs at velocity ratios (defined from the mean jet exit velocity during expulsion) of about 3 when $Re_d=2500$ and about 2 when $Re_d=5000$. This study presents evidence that the forcing effectiveness is maximised when the vortex street is most tilted into the streamwise direction.

The linear stability of miscible displacement for radial source flow at infinite Péclet number in a Hele-Shaw cell is calculated theoretically. The axisymmetric self-similar flow is shown to be unstable to viscous fingering if the viscosity ratio $m$ between ambient and injected fluids exceeds $3/2$, and to be stable if $m\lt {3/2}$. If $1\lt m\lt {3/2}$, then small disturbances decay at rates between $t^{-3/4}$ and $t^{-1}$ (the exact range depending on $m$) relative to the $t^{1/2}$ radius of the axisymmetric base-state similarity solution; if $m\lt 1$, then they decay faster than $t^{-1}$. Asymptotic analysis confirms these results and gives physical insight into various features of the numerically determined relationship between the growth rate and the azimuthal wavenumber and viscosity ratio.

The evolution of turbulent spots in a flat plate boundary layer is examined using time-resolved tomographic particle image velocimetry (Tomo-PIV) experiments and direct numerical simulation (DNS). The characteristics of flow structures are examined using timelines and material surfaces. Both the numerical and experimental results reveal a notable behaviour in the developmental process of turbulent spots: the development of low-speed streaks at the spanwise edges of turbulent spots, followed by the subsequent formation of hairpin vortices. The behaviour of these low-speed streaks is further investigated using timelines and material surfaces generated for a series of regions and development times. The results indicate that these low-speed streaks exhibit characteristic wave behaviour. The low-speed streaks are observed to lift up as three-dimensional (3-D) waves, with high-shear layers forming at the interface of these waves. These induced high-shear layers become unstable and evolve into vortices, which contribute to the expansion of the turbulent spot. These findings show the significant role of 3-D waves in the development of turbulent spots, supporting the hypothesis that 3-D waves serve as initiators of vortices at the bounding surface of a turbulent spot.

Using clean numerical simulation (CNS) in which artificial numerical noise is negligible over a finite, sufficiently long interval of time, we provide evidence, for the first time, that artificial numerical noise in direct numerical simulation (DNS) of turbulence is approximately equivalent to thermal fluctuation and/or stochastic environmental noise. This confers physical significance on the artificial numerical noise of DNS of the Navier–Stokes equations. As a result, DNS on a fine mesh should correspond to turbulence under small internal/external physical disturbance, whereas DNS on a sparse mesh corresponds to turbulent flow under large physical disturbance. The key point is that all of them have physical meanings and so are correct in terms of their deterministic physics, even if their statistics are quite different. This is illustrated herein. Our paper provides a positive viewpoint regarding the presence of artificial numerical noise in DNS.

We study the onset of spontaneous dynamics in the follower force model of an active filament, wherein a slender elastic filament in a viscous liquid is clamped normal to a wall at one end and subjected to a tangential compressive force at the other. Clarke et al. (Phys. Rev. Fluids, vol. 9, 2024, 073101) recently conducted a thorough investigation of this model using methods of computational dynamical systems; inter alia, they showed that the filament first loses stability via a supercritical double-Hopf bifurcation, with periodic ‘planar-beating’ states (unstable) and ‘whirling’ states (stable) simultaneously emerging at the critical follower-force value. We complement their numerical study by carrying out a weakly nonlinear analysis close to this unconventional bifurcation, using the method of multiple scales. The main outcome is an ‘amplitude equation’ governing the slow modulation of small-magnitude oscillations of the filament in that regime. Analysis of this reduced-order model provides insights into the onset of spontaneous dynamics, including the creation of the nonlinear whirling states from particular superpositions of linear planar-beating modes as well as the selection of whirling over planar beating in three-dimensional scenarios.

We perform simulations of a two-fluid–structure interaction problem involving liquid–gas flow past a fully submerged stationary circular cylinder. Interactions between the liquid–gas interface with finite surface tension and flow disturbances arising from the cylinder induce a variety of interfacial phenomena and wake structures. We map different interface regimes in a parameter space defined by the Bond number $Bo \in [100, 5000]$ and the submergence depth $h/D \in [1, 2.5]$ of the cylinder while keeping the Reynolds (Re) and Weber (We) numbers fixed at 150 and 1000, respectively. The emerging interface features are classified into three distinct regimes: interfacial waves generated by Strouhal vortices, the entrainment of multi-scale gas bubbles and the reduced deformation state. In the interfacial wave regime, we demonstrate that the frequency of transverse interface fluctuations at a specific streamwise location is identical to the vortex shedding frequency. Additionally, the wavelength of interfacial waves is determined by the size of vortex pairs consisting of alternating Strouhal vortices. In the gas entrainment regime at $ Bo = 1000$, our bubble-size distributions reveal that the entrained bubbles have sizes ranging from one to two orders of magnitude smaller than the cylinder. These multi-scale bubbles are formed primarily through plunging and surfing breakers at $h/D = 2.5$. In contrast, at $h/D = 1$, smaller bubbles initially emerge from the breakup of a gas finger. Over time, some of these bubbles grow in size through coalescence cascades. The influence of $ Re \in [50, 150]$ and $ We \in [700, 1100]$ on gas entrainment is quantified in terms of mean bubble size and count. Lastly, we demonstrate how the deformability of the liquid–gas interface drives the hydrodynamic lift force acting on the cylinder. The net downward lift materializes only in the gas entrainment and reduced deformation regimes due to the broken symmetry of the front stagnation point. While our study focuses on two-dimensional simulations, we also provide insights into the three-dimensional gas entrainment mechanism for one of the extreme cases at $h/D = 1$.

Particle-laden horizontal turbulent pipe flow is studied experimentally in the two-way coupling regime with a focus on delineating the effects of particle-to-fluid density ratio $\rho _{p}/\rho _{f}=1$ and 1.05 on the fluid and particle statistics. Particle volume fraction $\phi _{v}$ up to $1\,\%$ and viscous Stokes numbers ranging from $St^+ \approx 1.2$ to $St^+ \approx 3.8$ are investigated at friction Reynolds number $Re_\tau \approx 195$ using time-resolved two-dimensional particle image and tracking velocimetry. Substantial differences are observed between the statistics of neutrally buoyant (i.e. $\rho _{p}/\rho _{f}=1$) and denser (i.e. $\rho _{p}/\rho _{f}=1.05$) settling particles (with settling velocities 0.12–0.32 times the friction velocity), which, at most instances, show opposing trends compared to unladen pipe flow statistics. Neutrally buoyant particles show a slightly increased overall drag and suppressed turbulent stresses, but elevated particle–fluid interaction drag and results in elongated turbulent structures compared to the unladen flow, whereas $\rho _{p}/\rho _{f}=1.05$ particles exhibit a slight overall drag reduction even with increased radial turbulent stresses, and shorter streamwise structures compared to the unladen flow. These differences are enhanced with increasing $St^+$ and $\phi _v$, and can be attributed to the small but non-negligible settling velocity of denser particles, which also leads to differing statistics in the upper and lower pipe halves.

We conduct direct numerical simulations (DNS) to investigate the attenuation of turbulence in a periodic cube due to the addition of prolate spheroidal solid particles. Even with a dilute volume fraction of $O(10^{-2})$, particles can drastically attenuate the turbulence. Our DNS show that the turbulent kinetic energy reduces more significantly when the particles’ Stokes number is larger, size is smaller or aspect ratio is larger. We can explain these results based on the formula proposed by Oka and Goto (2022 J. Fluid Mech. 949, A45), which relates the turbulence attenuation rate to the energy dissipation rate $\epsilon _p$ around particles. More precisely, under the condition that the volume fraction of particles is fixed, $\epsilon _p$ is larger when the Stokes number and, therefore, the relative velocity between fluid and particles are larger, the particle size is smaller or the aspect ratio is larger. These results also imply that the rotation of the anisotropic particles plays only a limited role in the attenuation of turbulence when the Stokes number of particles is sufficiently large, because the main cause of the attenuation is the relative translational velocity between fluid and particles.

Rogue waves (RWs) can form on the ocean surface due to the well-known quasi-four-wave resonant interaction or superposition principle. The first is known as the nonlinear focusing mechanism and leads to an increased probability of RWs when unidirectionality and narrowband energy of the wave field are satisfied. This work delves into the dynamics of extreme wave focusing in crossing seas, revealing a distinct type of nonlinear RWs, characterised by a decisive longevity compared with those generated by the dispersive focusing (superposition) mechanism. In fact, through fully nonlinear hydrodynamic numerical simulations, we show that the interactions between two crossing unidirectional wave beams can trigger fully localised and robust development of RWs. These coherent structures, characterised by a typical spectral broadening then spreading in the form of dual bimodality and recurrent wave group focusing, not only defy the weakening expectation of quasi-four-wave resonant interaction in directionally spreading wave fields, but also differ from classical focusing mechanisms already mentioned. This has been determined following a rigorous lifespan-based statistical analysis of extreme wave events in our fully nonlinear simulations. Utilising the coupled nonlinear Schrödinger framework, we also show that such intrinsic focusing dynamics can be captured by weakly nonlinear wave evolution equations. This opens new research avenues for further explorations of these complex and intriguing wave phenomena in hydrodynamics as well as other nonlinear and dispersive multi-wave systems.

Turbulent flows over porous substrates are studied via a systematic exploration of the dependence of the flow properties on the substrate parameters, including permeability $K$, grain pitch $L$ and depth $h$. The study uses direct numerical simulations mainly for staggered-cube substrates with $L^+\approx 10$–$50$, $\sqrt {K}/L\approx 0.01$–$0.25$ and depths from $h=O(L)$ to $h\gg L$, ranging from typical impermeable rough surfaces to deep porous substrates. The results indicate that the permeability has significantly greater relevance than the grain size and microscale topology for the properties of the overlying flow, including the mean-flow slip and the shear across the interface, the drag increase relative to smooth-wall flow and the statistics and spectra of the overlying turbulence, whereas the direct effect of grain size is only noticeable near the interface as grain-coherent flow fluctuations. The substrate depth also has a significant effect, with shallower substrates suppressing the effective transpiration at the interface. Based on the direct-simulation results, we propose an empirical ‘equivalent permeability’ $K_{eq}^t$ that incorporates this effect and scales well the overlying turbulence for substrates with different depths, permeabilities, etc. This result suggests that wall normal transpiration driven by pressure fluctuations is the leading contributor to the changes in the drag and the overlying turbulence. Based on this, we propose a conceptual $h^+$–$\sqrt {K^+}$ regime diagram where, for any given substrate topology, turbulence transitions smoothly from that over impermeable rough surfaces with $h=O(L)$ to that over deep porous substrates with $h^+\gtrsim 50$, with the latter limit determined by the typical lengthscale of the overlying pressure fluctuations.

As new concepts to protect marine structures from ocean waves, we propose the use of a floating elastic annulus. In this paper, two types of annuli are demonstrated. The first is a ‘wave shield’, which creates a calm free surface within an inner domain of the annulus by preventing wave penetration. The second is a ‘cloak’, which not only creates a calm space within the inner domain but also prevents wave scattering outside the annulus. To evaluate the calmness of the inner domain of the annulus, an inlet wave energy factor is newly defined. The wave shield is designed to minimise the inlet wave energy factor to nearly zero. However, the cloak is designed to minimise both the inlet wave energy factor and scattered-wave energy which evaluates the amount of wave scattering at far-field. Each annulus consists of several horizontal concentric annular plates, and the flexural rigidities of the plates are optimised to minimise objective functions at a target frequency. Numerical simulations demonstrate that both the wave shield and the cloak can create calm free surfaces within their inner domains. In addition, the cloak effectively suppresses the outgoing scattering waves and reduces the resultant wave drift force.

Lift and drag forces on moving intruders in flowing granular materials are of fundamental interest but have not yet been fully characterized. Drag on an intruder in granular shear flow has been studied almost exclusively for the intruder moving across flow streamlines, and the few studies of the lift explore a relatively limited range of parameters. Here, we use discrete element method simulations to measure the lift force, $F_{{L}}$, and the drag force on a spherical intruder in a uniformly sheared bed of smaller spheres for a range of streamwise intruder slip velocities, $u_{{s}}$. The streamwise drag matches the previously characterized Stokes-like cross-flow drag. However, $F_{{L}}$ in granular shear flow acts in the opposite direction to the Saffman lift in a sheared fluid at low $u_{{s}}$, reaches a maximum value and then decreases with increasing $u_{{s}}$, eventually reversing direction. This non-monotonic response holds over a range of flow conditions, and the $F_{{L}}$ versus $u_{{s}}$ data collapse when both quantities are scaled using the particle size, shear rate and overburden pressure. Analogous fluid simulations demonstrate that the flow around the intruder particle is similar in the granular and fluid cases. However, the shear stress on the granular intruder is notably less than that in a fluid shear flow. This difference, combined with a void behind the intruder in granular flow in which the stresses are zero, significantly changes the lift-force-inducing stresses acting on the intruder between the granular and fluid cases.

In Rayleigh–Bénard convection and Taylor–Couette flow cellular patterns emerge at the onset of instability and persist as large-scale coherent structures in the turbulent regime. Their long-term dynamics has been thoroughly characterised and modelled for the case of turbulent convection, whereas turbulent Taylor rolls have received much less attention. Here we present direct numerical simulations of axisymmetric Taylor–Couette flow in the corotating regime and reveal a transition to spatio–temporal chaos as the system size increases. Beyond this transition, Taylor rolls suddenly undergo erratic drifts evolving on a very slow time scale. We estimate an effective diffusion coefficient for the drift and compare the dynamics with analogous motions in Rayleigh–Bénard convection and Poiseuille flow, suggesting that this spontaneous diffusive displacement of large coherent structures is common among different types of wall-bounded turbulent flows.

Wind turbines operate in the atmospheric boundary layer (ABL), where Coriolis effects are present. As wind turbines with larger rotor diameters are deployed, the wake structures that they create in the ABL also increase in length. Contemporary utility-scale wind turbines operate at rotor diameter-based Rossby numbers, the non-dimensional ratio between inertial and Coriolis forces, of $\mathcal {O}(100)$ where Coriolis effects become increasingly relevant. Coriolis forces provide a direct forcing on the wake, but also affect the ABL base flow, which indirectly influences wake evolution. These effects may constructively or destructively interfere because both the magnitude and sign of the direct and indirect Coriolis effects depend on the Rossby number, turbulence and buoyancy effects in the ABL. Using large eddy simulations, we investigate wake evolution over a wide range of Rossby numbers relevant to offshore wind turbines. Through an analysis of the streamwise and lateral momentum budgets, we show that Coriolis effects have a small impact on the wake recovery rate, but Coriolis effects induce significant wake deflections which can be parsed into two regimes. For high Rossby numbers (weak Coriolis forcing), wakes deflect clockwise in the northern hemisphere. By contrast, for low Rossby numbers (strong Coriolis forcing), wakes deflect anti-clockwise. Decreasing the Rossby number results in increasingly anti-clockwise wake deflections. The transition point between clockwise and anti-clockwise deflection depends on the direct Coriolis forcing, pressure gradients and turbulent fluxes in the wake. At a Rossby number of 125, Coriolis deflections are comparable to wake deflections induced by ${\sim} 20^{\circ }$ of yaw misalignment.

Active fluids encompass a wide range of non-equilibrium fluids, in which the self-propulsion or rotation of their units can give rise to large-scale spontaneous flows. Despite the diversity of active fluids, they are commonly viscoelastic. Therefore, we develop a hydrodynamic model of isotropic active liquids by accounting for their viscoelasticity. Specifically, we incorporate an active stress term into a general viscoelastic liquid model to study the spontaneous flow states and their transitions in two-dimensional channel, annulus and disk geometries. We have discovered rich spontaneous flow states in a channel as a function of activity and Weissenberg number, including unidirectional flow, travelling-wave and vortex-roll states. The Weissenberg number acts against activity by suppressing the spontaneous flow. In an annulus confinement, we find that a net flow can be generated only if the aspect ratio of the annulus is not too large nor too small, akin to some three-dimensional active-flow phenomena. In a disk geometry, we observe a periodic chirality switching of a single vortex flow, resembling the bacteria-based active fluid experiments. The two phenomena reproduced in our model differ in Weissenberg number and frictional coefficient. As such, our active viscoelastic model offers a unified framework to elucidate diverse active liquids, uncover their connections and highlight the universality of dynamic active-flow patterns.

We study the response of a flexible prism with a square cross-section placed in cross-flow through a series of experiments conducted at increasing flow velocities. We show that as the reduced velocity (a dimensionless flow velocity that also depends on the natural frequency of the structure) is increased, the prism undergoes vortex-induced vibration (VIV) in its first mode, which then transitions to VIV in the second mode and then third mode. In these ranges, the shedding frequency is synchronised with the oscillation frequency, and the oscillations are mainly in the transverse (cross-flow – CF) direction. As we keep increasing the reduced velocity, we observe a linear increase in the amplitude of the torsional oscillations of the prism, resembling a torsional galloping. This increase in the torsional oscillations then causes an increase in the amplitudes of the CF and inline (IL) oscillations while the third structural mode is still excited in the CF direction. A transition to oscillations in the fourth structural mode is observed at higher reduced velocities, which reduces the CF and IL amplitudes, while the torsional oscillations reach a plateau. After this plateau is reached in the torsional oscillations, galloping is observed in the CF oscillations of the response, which results in large-amplitude oscillations in both the CF and IL directions. The CF galloping response at these higher reduced velocities is accompanied by a torsional VIV response and the shedding frequency is synchronised with the frequency of the torsional oscillations.