Starting from the coupled Boltzmann–Enskog (BE) kinetic equations for a two-particle system consisting of hard spheres, a hyperbolic two-fluid model for binary, hard-sphere mixtures was derived in Fox (2019, J. Fluid Mech. 877, 282). In addition to spatial transport, the BE kinetic equations account for particle–particle collisions, using an elastic hard-sphere collision model, and the Archimedes (buoyancy) force due to spatial gradients of the pressure in each phase, as well as other forces involving spatial gradients. The ideal-fluid–particle limit of this model is found by letting one of the particle diameters go to zero while the other remains finite. The resulting two-fluid model has closed terms for the spatial fluxes and momentum exchange due to the excluded volume occupied by the particles, e.g. a momentum-exchange term 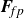$\boldsymbol {F}_{\!\!fp}$ that depends on gradients of the fluid density 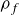$\rho _f$, fluid velocity 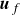$\boldsymbol{u}_{f}$ and fluid pressure $p_f$. In Zhang et al. (2006, Phy. Rev. Lett. 97, 048301), the corresponding unclosed momentum-exchange term depends on the divergence of an unknown particle–fluid–particle (pfp) stress (or pressure) tensor. 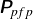Here, it is shown that the pfp-pressure tensor ${\unicode{x1D64B}}_{\!pfp}$ can be found in closed form from the expression for 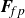$\boldsymbol {F}_{\!\!fp}$ derived in Fox (2019, J. Fluid Mech. 877, 282). Remarkably, using this expression for 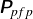${\unicode{x1D64B}}_{\!pfp}$ ensures that the two-fluid model for ideal-fluid–particle flow is well posed for all fluid-to-particle material-density ratios 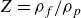$Z = \rho _f / \rho _p$.

The propulsive efficiency of flying and swimming animals propelled by oscillatory appendages typically peaks within a narrow Strouhal number range of $0.20 \lt St \lt 0.40$. Motivated by the ubiquitous presence of stratification in natural environments, we numerically investigate the optimal Strouhal numbers $S{t_m}$ for an oscillating foil in density stratified fluids. Our results reveal that $S{t_m}$ increases with the strength of stratification characterised by the internal Froude number $Fr$, giving rise to markedly higher values under strong stratifications compared with those observed in homogeneous fluids. The propulsive efficiency tends to maximise when there is a resonance between the oscillations of the foil and the fluid, as inferred from a fitted line in the ($St$, $Fr$) parameter space, which shows that $S{t_m}$ is proportional to $Fr^{-1}$. We further uncover that the significant increase in $S{t_m}$ in strongly stratified regimes is fundamentally driven by fluid entrainment. During this process, the oscillating foil induces perturbations in the density field, resulting in buoyancy-driven restoring forces which alter the pressure distribution on the foil and thus the hydrodynamic forces. Notably, only under strongly stratified conditions, where dominant buoyancy effects confine the density transport to the vicinity of the oscillating foil, the intensified density perturbation due to the increase in $St$ can be effectively harnessed to enhance thrust production, thereby contributing to the elevated $S{t_m}$. These insights suggest that oscillatory propulsors should adopt new kinematic strategies involving relatively large Strouhal numbers to achieve efficient cruising in strongly stratified environments.

In fluid dynamics, helicity measures the correlation between velocity and its curl, vorticity, over a spatial volume. Under ‘ideal’ conditions (vanishing viscosity and either homogeneneous density or when pressure may be regarded as a function of density alone), helicity is a topological invariant closely related to the knottedness of vortex lines (Moffatt 1969 J. Fluid Mech. 35 (1), 117–129). Helicity is conserved following a material volume for compact vorticity distributions, i.e. when the vorticity field is tangent to the surface of the volume. There is a related helicity invariant in ideal magnetohydrodynamics involving the correlation between the magnetic potential and its curl, the magnetic field. Helicity is a fragile invariant in the sense that relaxing any one of the ideal conditions results in non-conservation. Unlike energy and enstrophy (mean-square vorticity), helicity is not positive (or sign) definite. Viscous diffusion can create both positive and negative helicity when vortex lines reconnect, something which is topologically forbidden in an ideal fluid where vortex lines move as material curves. Moreover, variable density or more generally compressibility destroys conservation and weakens the association between helicity and vortex-line topology. Furthermore, in compressible flows, the velocity field is not entirely determined from the vorticity field. A recent paper by Boutros & Gibbon (2025) J. Fluid Mech. in this journal explains how one can extend the definition of helicity to control and limit the non-conservation of helicity. This offers a promising way forward in using helicity to characterise flow properties in computational studies of high Reynolds number flows.

We present a mathematical model to investigate heat transfer and mass transport dynamics in the wave-driven free-surface boundary layer of the ocean under the influence of long-crested progressive surface gravity waves. The continuity, momentum and convection–diffusion equations for fluid temperature are solved within a Lagrangian framework. We assume that eddy viscosity and thermometric conductivity are dependent on Lagrangian coordinates, and derive a new form of the second-order Lagrangian mass transport velocity, applicable across the entire finite water depth. We then analyse the convective heat dynamics influenced by the free-surface boundary layer. Rectangular distributions of free-surface temperature (i.e. a Dirichlet boundary condition) are considered, and analytical solutions for thermal boundary layer temperature fields are provided to offer insights into free-surface heat transfer mechanisms affected by ocean waves. Our results suggest the need to improve existing models that neglect the effects of free-surface waves and the free-surface boundary layer on ocean mass transport and heat transfer.