Building on our previous work on enriched universal algebra, we define a notion of enriched language consisting of function and relation symbols whose arities are objects of the base of enrichment $\mathcal {V}$. In this context, we construct atomic formulas and define the regular fragment of our enriched logic by taking conjunctions and existential quantification of those. We then characterize $\mathcal {V}$-categories of models of regular theories as enriched injectivity classes in the $\mathcal {V}$-category of structures. These notions rely on the choice of an orthogonal factorization system $(\mathcal {E},\mathcal {M})$ on $\mathcal {V}$ which will be used, in particular, to interpret relation symbols and existential quantification.

Homotopy type theory (HoTT) enables reasoning about groups directly as the types of symmetries (automorphisms) of mathematical structures. The HoTT approach to groups—first put forward by Buchholtz, van Doorn, and Rijke—identifies a group with the type of objects of which it is the symmetries. This type is called the “delooping” of the group, taking a term from algebraic topology. This approach naturally extends the group theory to higher groups which have symmetries between symmetries, and so on. In this paper, we formulate and prove a higher version of Schreier’s classification of all group extensions of a given group. Specifically, we prove that extensions of a group G by a group K are classified by actions of G on a delooping of K. Our proof is formalized in Cubical Agda, a dependently typed programming language and proof assistant which implements HoTT.

This paper focuses on the structurally complete extensions of the system $\mathbf {R}$-mingle ($\mathbf {RM}$). The main theorem demonstrates that the set of all hereditarily structurally complete extensions of $\mathbf {RM}$ is countably infinite and forms an almost-chain, with only one branching element. As a corollary, we show that the set of structurally complete extensions of $\mathbf {RM}$ that are not hereditary is also countably infinite and forms a chain. Using algebraic methods, we provide a complete description of both sets. Furthermore, we offer a characterization of passive structural completeness among the extensions of $\mathbf {RM}$: specifically, we prove that a quasivariety of Sugihara algebras is passively structurally complete if and only if it excludes two specific algebras. As a corollary, we give an additional characterization of quasivarieties of Sugihara algebras that are passively structurally complete but not structurally complete. We close the paper with a characterization of actively structurally complete quasivarieties of Sugihara algebras.

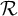We investigate Steel’s conjecture in ‘The Core Model Iterability Problem’ [10], that if $\mathcal {W}$ and $\mathcal {R}$ are 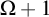$\Omega +1$-iterable, $1$-small weasels, then $\mathcal {W}\leq ^{*}\mathcal {R}$ iff there is a club $C\subset \Omega $ such that for all 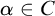$\alpha \in C$, if 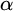$\alpha $ is regular, then 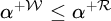$\alpha ^{+\mathcal {W}}\leq \alpha ^{+\mathcal {R}}$. We will show that the conjecture fails, assuming that there is an iterable premouse M which models KP and which has a -Woodin cardinal. On the other hand, we show that assuming there is no transitive model of KP with a Woodin cardinal the conjecture holds. In the course of this we will also show that if M is a premouse which models KP with a largest, regular, uncountable cardinal $\delta $, and $\mathbb {P} \in M$ is a forcing poset such that $M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$, and $g\subset \mathbb {P}$ is M-generic, then $M[g]\models \text {KP}$. Additionally, we study the preservation of admissibility under iteration maps. At last, we will prove a fact about the closure of the set of ordinals at which a weasel has the S-hull property. This answers another question implicit in remarks in [10].

This paper studies which truth-values are most likely to be taken on finite models by arbitrary sentences of a many-valued predicate logic. The classical zero-one law (independently proved by Fagin and Glebskiĭ et al.) states that every sentence in a purely relational language is almost surely false or almost surely true, meaning that the probability that the formula is true in a randomly chosen finite structures of cardinal n is asymptotically $0$ or $1$ as n grows to infinity. We obtain generalizations of this result for any logic with values in a finite lattice-ordered algebra, and for some infinitely valued logics, including Łukasiewicz logic. The finitely valued case is reduced to the classical one through a uniform translation and Oberschelp’s generalization of the zero-one law. Moreover, it is shown that the complexity of determining the almost sure value of a given sentence is PSPACE-complete (generalizing Grandjean’s result for the classical case), and for some logics we describe completely the set of truth-values that can be taken by sentences almost surely.

We study versions of the tree pigeonhole principle, $\mathsf {TT}^1$, in the context of Weihrauch-style computable analysis. The principle has previously been the subject of extensive research in reverse mathematics, an outstanding question of which investigation is whether $\mathsf {TT}^1$ is $\Pi ^1_1$-conservative over the ordinary pigeonhole principle, $\mathsf {RT}^1$. Using the recently introduced notion of the first-order part of an instance-solution problem, we formulate the analog of this question for Weihrauch reducibility, and give an affirmative answer. In combination with other results, we use this to show that unlike $\mathsf {RT}^1$, the problem $\mathsf {TT}^1$ is not Weihrauch requivalent to any first-order problem. Our proofs develop new combinatorial machinery for constructing and understanding solutions to instances of $\mathsf {TT}^1$.

We characterize the epimorphisms in homotopy type theory (HoTT) as the fiberwise acyclic maps and develop a type-theoretic treatment of acyclic maps and types in the context of synthetic homotopy theory as developed in univalent foundations. We present examples and applications in group theory, such as the acyclicity of the Higman group, through the identification of groups with 0-connected, pointed 1-types. Many of our results are formalized as part of the agda-unimath library.

We investigate natural variations of behaviourally correct learning and explanatory learning—two learning paradigms studied in algorithmic learning theory—that allow us to “learn” equivalence relations on Polish spaces. We give a characterization of the learnable equivalence relations in terms of their Borel complexity and show that the behaviourally correct and explanatory learnable equivalence relations coincide both in uniform and non-uniform versions of learnability and provide a characterization of the learnable equivalence relations in terms of their Borel complexity. We also show that the set of uniformly learnable equivalence relations is $\boldsymbol {\Pi }^1_1$-complete in the codes and study the learnability of several equivalence relations arising naturally in logic as a case study.

We show that in the Silver model the inequality $\mathrm {cov}(\mathfrak {C} _2) < \mathrm {cov}(\mathfrak {P}_2)$ holds true, where $\mathfrak {C}_2$ and $\mathfrak {P}_2$ are the two-dimensional Mycielski ideals.

In [2], Pillay introduced definable Galois cohomology, a model-theoretic generalization of Galois cohomology. Let M be an atomic and strongly $\omega $-homogeneous structure over a set of parameters A. Let B be a normal extension of A in M. We show that a short exact sequence of automorphism groups $1 \to \operatorname {\mathrm {Aut}}(M/B) \to \operatorname {\mathrm {Aut}}(M/A) \to \operatorname {\mathrm {Aut}}(B/A) \to 1$ induces a short exact sequence in definable Galois cohomology. We also discuss compatibilities with [3]. Our result complements the long exact sequence in definable Galois cohomology developed in [4].

We contribute to the study of generalizations of the Perfect Set Property and the Baire Property to subsets of spaces of higher cardinalities, like the power set ${\mathcal {P}}({\lambda })$ of a singular cardinal $\lambda $ of countable cofinality or products $\prod _{i<\omega }\lambda _i$ for a strictly increasing sequence $\langle {\lambda _i}~\vert ~{i<\omega }\rangle $ of cardinals. We consider the question under which large cardinal hypothesis classes of definable subsets of these spaces possess such regularity properties, focusing on rank-into-rank axioms and classes of sets definable by $\Sigma _1$-formulas with parameters from various collections of sets. We prove that $\omega $-many measurable cardinals, while sufficient to prove the perfect set property of all $\Sigma _1$-definable sets with parameters in $V_\lambda \cup \{V_\lambda \}$, are not enough to prove it if there is a cofinal sequence in $\lambda $ in the parameters. For this conclusion, the existence of an I2-embedding is enough, but there are parameters in $V_{\lambda +1}$ for which I2 is still not enough. The situation is similar for the Baire property: under I2 all sets that are $\Sigma _1$-definable using elements of $V_\lambda $ and a cofinal sequence as parameters have the Baire property, but I2 is not enough for some parameter in $V_{\lambda +1}$. Finally, the existence of an I0-embedding implies that all sets that are $\Sigma ^1_n$-definable with parameters in $V_{\lambda +1}$ have the Baire property.

In $\mathsf {ZF}$ (i.e., Zermelo–Fraenkel set theory minus the axiom of choice ($\mathsf {AC}$)), we investigate the open problem of the deductive strength of the principle

which was introduced by Herzberg, Kanovei, Katz, and Lyubetsky [(2018), Journal of Symbolic Logic, 83(1), 385–391]. Typical results are:

1. (1) “$\aleph _{1}\leq 2^{\aleph _{0}}$” is strictly weaker than $\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$.

2. (2) “There exists a free ultrafilter on $\omega $” does not imply “$\aleph _{1}\leq 2^{\aleph _{0}}$” in $\mathsf {ZF}$, and thus (by (1)) neither does it imply $\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$. This fills the gap in information in Howard and Rubin [Mathematical Surveys and Monographs, American Mathematical Society, 1998], as well as in Herzberg et al. (2018).

3. (3) Martin’s Axiom ($\mathsf {MA}$) implies “no free ultrafilter on $\omega $ has a well-orderable base of cardinality $<2^{\aleph _{0}}$”, and the latter principle is not implied by $\aleph _{0}$-Martin’s Axiom ($\mathsf {MA}(\aleph _{0})$) in $\mathsf {ZF}$.

4. (4) $\mathsf {MA} + \mathsf {UF_{wob}}(\omega )$ implies $\mathsf {AC}(\mathbb {R})$ (the axiom of choice for non-empty sets of reals), which in turn implies $\mathsf {UF_{wob}}(\omega )$. Furthermore, $\mathsf {MA}$ and $\mathsf {UF_{wob}}(\omega )$ are mutually independent in $\mathsf {ZF}$.

5. (5) For any infinite linearly orderable set X, each of “every filter base on X can be well ordered” and “every filter on X has a well-orderable base” is equivalent to “$\wp (X)$ can be well ordered”. This yields novel characterizations of the principle “every linearly ordered set can be well ordered” in $\mathsf {ZFA}$ (i.e., Zermelo–Fraenkel set theory with atoms), and of $\mathsf {AC}$ in $\mathsf {ZF}$.

6. (6) “Every filter on $\mathbb {R}$ has a well-orderable base” implies “every filter on $\omega $ has a well-orderable base”, which in turn implies $\mathsf {UF_{wob}}(\omega )$, and none of these implications are reversible in $\mathsf {ZF}$.

7. (7) “Every filter on $\omega $ can be extended to an ultrafilter with a well-orderable base” is equivalent to $\mathsf {AC}(\mathbb {R}),$ and thus is strictly stronger than $\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$.

8. (8) “Every filter on $\omega $ can be extended to an ultrafilter” implies “there exists a free ultrafilter on $\omega $ which has no well-orderable base of cardinality ${<2^{\aleph _{0}}}$”. The former principle does not imply “there exists a free ultrafilter on $\omega $ which has no well-orderable base” in $\mathsf {ZF}$, and the latter principle is true in the Basic Cohen Model.

We explore the interplay between $\omega $-categoricity and pseudofiniteness for groups, and we conjecture that $\omega $-categorical pseudofinite groups are finite-by-abelian-by-finite. We show that the conjecture reduces to nilpotent p-groups of class 2, and give a proof that several of the known examples of $\omega $-categorical p-groups satisfy the conjecture. In particular, we show by a direct counting argument that for any odd prime p the ($\omega $-categorical) model companion of the theory of nilpotent class 2 exponent p groups, constructed by Saracino and Wood, is not pseudofinite, and that an $\omega $-categorical group constructed by Baudisch with supersimple rank 1 theory is not pseudofinite. We also survey some scattered literature on $\omega $-categorical groups over 50 years.

We investigate the tower spectrum in the generalized Baire space, i.e., the set of lengths of towers in $\kappa ^\kappa $. We show that both small and large tower spectra at all regular cardinals simultaneously are consistent. Furthermore, based on previous work by Bağ, the first author and Friedman, we prove that globally, a small tower spectrum is consistent with an arbitrarily large spectrum of maximal almost disjoint families. Finally, we show that any non-trivial upper bound on the tower spectrum in $\kappa ^\kappa $ is consistent.

Condensed mathematics, developed by Clausen and Scholze over the last few years, proposes a generalization of topology with better categorical properties. It replaces the concept of a topological space by that of a condensed set, which can be defined as a sheaf for the coherent topology on a certain category of compact Hausdorff spaces. In this case, the sheaf condition has a fairly simple explicit description, which arises from studying the relationship between the coherent, regular, and extensive topologies. In this paper, we establish this relationship under minimal assumptions on the category, going beyond the case of compact Hausdorff spaces. Along the way, we also provide a characterization of sheaves and covering sieves for these categories. All results in this paper have been fully formalized in the Lean proof assistant.

It is a classic result of Segerberg and Maksimova that a variety of $\mathsf {S4}$-algebras is locally finite iff it is of finite depth. Since the logic $\mathsf {MS4}$ (monadic $\mathsf {S4}$) axiomatizes the one-variable fragment of $\mathsf {QS4}$ (predicate $\mathsf {S4}$), it is natural to try to generalize the Segerberg–Maksimova theorem to this setting. We obtain several results in this direction. Our positive results include the identification of the largest semisimple variety of $\mathsf {MS4}$-algebras. We prove that the corresponding logic $\mathsf {MS4_S}$ has the finite model property. We show that both $\mathsf {S5}^2$ and $\mathsf {S4}_u$ are proper extensions of $\mathsf {MS4_S}$, and that a direct generalization of the Segerberg–Maksimova theorem holds for a family of varieties containing the variety of $\mathsf {S4}_u$-algebras. Our negative results include a translation of varieties of $\mathsf {S5}_2$-algebras into varieties of $\mathsf {MS4_S}$-algebras of depth 2, which preserves and reflects local finiteness. This, in particular, shows that the problem of characterizing locally finite varieties of $\mathsf {MS4}$-algebras (even of $\mathsf {MS4_S}$-algebras) is at least as hard as that of characterizing locally finite varieties of $\mathsf {S5}_2$-algebras—a problem that remains wide open.

We study the question of $\mathcal {L}_{\mathrm {ring}}$-definability of non-trivial henselian valuation rings. Building on previous work of Jahnke and Koenigsmann, we provide a characterization of henselian fields that admit a non-trivial definable henselian valuation. In particular, we treat the cases where the canonical henselian valuation has positive residue characteristic, using techniques from the model theory and algebra of tame fields.

In this paper, we study the employment of $\Sigma _1$-sentences with certificates, i.e., $\Sigma _1$-sentences where a number of principles is added to ensure that the witness is sufficiently number-like. We develop certificates in some detail and illustrate their use by reproving some classical results and proving some new ones. An example of such a classical result is Vaught’s theorem of the strong effective inseparability of $\mathsf {R}_0$.

We also develop the new idea of a theory being $\mathsf {R}_{0\mathsf {p}}$-sourced. Using this notion, we can transfer a number of salient results from $\mathsf {R}_0$ to a variety of other theories.

We start by showing how to approximate unitary and bounded self-adjoint operators by operators in finite dimensional spaces. Using ultraproducts we give a precise meaning for the approximation. In this process we see how the spectral measure is obtained as an ultralimit of counting measures that arise naturally from the finite dimensional approximations. Then we see how generalized distributions can be interpreted in the ultraproduct. Finally we study how one can calculate kernels of operators K by calculating them in the finite dimensional approximations and how one needs to interpret Dirac deltas in the ultraproduct in order to get the kernels as propagators $\langle x_{1}|K|x_{0}\rangle $.

Reverse Mathematics (RM) is a program in the foundations of mathematics where the aim is to find the minimal axioms needed to prove a given theorem of ordinary mathematics. Generally, the minimal axioms are equivalent to the theorem at hand, assuming a weak logical system called the base theory. Moreover, many theorems are either provable in the base theory or equivalent to one of four logical systems, together called the Big Five. For instance, the Weierstrass approximation theorem, i.e., that a continuous function can be approximated uniformly by a sequence of polynomials, has been classified in RM as being equivalent to weak König’s lemma, the second Big Five system. In this paper, we study approximation theorems for discontinuous functions via Bernstein polynomials from the literature. We obtain many equivalences between the latter and weak König’s lemma. We also show that slight variations of these approximation theorems fall far outside of the Big Five but fit in the recently developed RM of new ‘big’ systems, namely the uncountability of ${\mathbb R}$, the enumeration principle for countable sets, the pigeon-hole principle for measure, and the Baire category theorem.