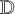Let $\mathcal {X}\to \mathbb {D}$ be a flat family of projective complex 3-folds over a disc $\mathbb {D}$ with smooth total space $\mathcal {X}$ and smooth general fibre $\mathcal {X}_t,$ and whose special fiber $\mathcal {X}_0$ has double normal crossing singularities, in particular, $\mathcal {X}_0=A\cup B$, with A, B smooth threefolds intersecting transversally along a smooth surface $R=A\cap B.$ In this paper, we first study the limit singularities of a $\delta $-nodal surface in the general fibre $S_t\subset \mathcal {X}_t$, when $S_t$ tends to the central fibre in such a way its $\delta $ nodes tend to distinct points in R. The result is that the limit surface $S_0$ is in general the union $S_0=S_A\cup S_B$, with $S_A\subset A$, $S_B\subset B$ smooth surfaces, intersecting on R along a $\delta $-nodal curve $C=S_A\cap R=S_B\cap B$. Then we prove that, under suitable conditions, a surface $S_0=S_A\cup S_B$ as above indeed deforms to a $\delta $-nodal surface in the general fibre of $\mathcal {X}\to \mathbb {D}$. As applications, we prove that there are regular irreducible components of the Severi variety of degree d surfaces with $\delta $ nodes in $\mathbb {P}^3$, for every $\delta \leqslant {d-1\choose 2}$ and of the Severi variety of complete intersection $\delta $-nodal surfaces of type $(d,h)$, with $d\geqslant h-1$ in $\mathbb {P}^4$, for every $\delta \leqslant {{d+3}\choose 3}-{{d-h+1}\choose 3}-1.$

Kontsevich ([Kir95, Problem 3.48]) conjectured that $\mathrm {BDiff}(M, \text {rel }\partial )$ has the homotopy type of a finite CW complex for all compact $3$-manifolds with nonempty boundary. Hatcher-McCullough ([HM97]) proved this conjecture when M is irreducible. We prove a homological version of Kontsevich’s conjecture. More precisely, we show that $\mathrm {BDiff}(M, \text {rel }\partial )$ has finitely many nonzero homology groups each finitely generated when M is a connected sum of irreducible $3$-manifolds that each have a nontrivial and non-spherical boundary.