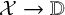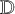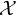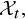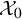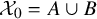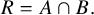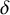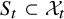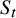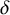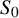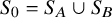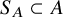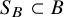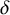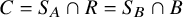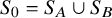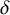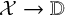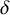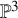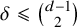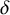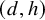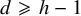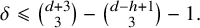1. Introduction
The main object of study in this article is Severi varieties of nodal surfaces on smooth, projective, complex threefolds. Severi varieties of nodal hypersurfaces on a smooth variety are a well-known object of study in algebraic geometry that goes back to well more than a century ago. Its importance is underlined by the relationships with other themes in the area. For example, the recent papers [Reference Di Gennaro and Franco7, Reference Thomas16] explore the relation of Severi varieties with the Hodge conjecture.
Our approach to the subject is via degenerations. Degenerations of smooth complex varieties to complex varieties with simple normal crossings is also a classical object of study. In particular, it has been widely used by several authors for studying Severi varieties of nodal curves on surfaces. The method is powerful and enables one to obtain sharp results on the non-emptiness of some Severi varieties of curves (see, for instance, [Reference Chen3, Reference Ciliberto, Dedieu, Galati and Knutsen5, Reference Ciliberto, Dedieu, Galati and Knutsen6, Reference Galati and Knutsen10], etc.).
One of the basic ideas in these papers is the well-known and classical fact that the limit of a curve
![]() $C_t$
with a node
$C_t$
with a node
![]() $p_t$
on a smooth surface
$p_t$
on a smooth surface
![]() $\mathcal {X}_t$
, when
$\mathcal {X}_t$
, when
![]() $\mathcal {X}_t$
degenerates to a reducible surface
$\mathcal {X}_t$
degenerates to a reducible surface
![]() $\mathcal {X}_0=A\cup B$
, with A and B smooth and meeting transversally along a smooth curve
$\mathcal {X}_0=A\cup B$
, with A and B smooth and meeting transversally along a smooth curve
![]() $R=A\cap B$
, and
$R=A\cap B$
, and
![]() $p_t$
going to a point
$p_t$
going to a point
![]() $p_0\in R$
, is a curve
$p_0\in R$
, is a curve
![]() $C_0\subset \mathcal {X}_0$
with a tacnode in
$C_0\subset \mathcal {X}_0$
with a tacnode in
![]() $p_0$
, which appears scheme theoretically with multiplicity
$p_0$
, which appears scheme theoretically with multiplicity
![]() $2$
. This result is an easy consequence of the study of the versal deformation space of a tacnode, and its proof is in [Reference Caporaso and Harris2, Reference Ran17]. This result has been proved also using limit linear systems techniques; see [Reference Galati9]. The present article intends to extend this result on the limit of a nodal curve to the case of nodal surfaces in threefolds, and we will take the point of view of [Reference Galati9]. In the sequel, a node of a surface will be an
$2$
. This result is an easy consequence of the study of the versal deformation space of a tacnode, and its proof is in [Reference Caporaso and Harris2, Reference Ran17]. This result has been proved also using limit linear systems techniques; see [Reference Galati9]. The present article intends to extend this result on the limit of a nodal curve to the case of nodal surfaces in threefolds, and we will take the point of view of [Reference Galati9]. In the sequel, a node of a surface will be an
![]() $A_1$
-singularity.
$A_1$
-singularity.
Let
![]() $\mathcal {X}\to \mathbb {D}$
be a flat family of projective complex 3-folds over a disc
$\mathcal {X}\to \mathbb {D}$
be a flat family of projective complex 3-folds over a disc
![]() $\mathbb {D}$
with smooth total space
$\mathbb {D}$
with smooth total space
![]() $\mathcal {X}$
and smooth general fibre, and whose special fiber
$\mathcal {X}$
and smooth general fibre, and whose special fiber
![]() $\mathcal {X}_0$
has double normal crossing singularities, in particular,
$\mathcal {X}_0$
has double normal crossing singularities, in particular,
![]() $\mathcal {X}_0=A\cup B$
, with A, B smooth threefolds intersecting transversally along a smooth surface
$\mathcal {X}_0=A\cup B$
, with A, B smooth threefolds intersecting transversally along a smooth surface
![]() $R=A\cap B.$
$R=A\cap B.$
First of all, we will study in Section 2 the limit singularities of a
![]() $\delta $
-nodal surface in the general fibre
$\delta $
-nodal surface in the general fibre
![]() $S_t\subset \mathcal {X}_t$
, when
$S_t\subset \mathcal {X}_t$
, when
![]() $S_t$
tends to the central fibre in such a way that its
$S_t$
tends to the central fibre in such a way that its
![]() $\delta $
nodes tend to distinct points
$\delta $
nodes tend to distinct points
![]() $p_1,\ldots ,p_\delta $
in R. The result (see Theorem 2.2) is that the limit surface
$p_1,\ldots ,p_\delta $
in R. The result (see Theorem 2.2) is that the limit surface
![]() $S_0$
is in general the union
$S_0$
is in general the union
![]() $S_0=S_A\cup S_B$
, with
$S_0=S_A\cup S_B$
, with
![]() $S_A\subset A$
,
$S_A\subset A$
,
![]() $S_B\subset B$
smooth surfaces, that cut out on R the same curve C having nodes at
$S_B\subset B$
smooth surfaces, that cut out on R the same curve C having nodes at
![]() $p_1,...,p_\delta $
and no further singularities. In this case, we say that
$p_1,...,p_\delta $
and no further singularities. In this case, we say that
![]() $S_0$
presents a singularity of type
$S_0$
presents a singularity of type
![]() $T_1$
at every point
$T_1$
at every point
![]() $p_i$
,
$p_i$
,
![]() $i=1,...,\delta $
. The equations of a
$i=1,...,\delta $
. The equations of a
![]() $T_1$
singularity are given in (2.9). Finally, in 2.4, we provide the local equation of (an example of) a local deformation of a singularity of type
$T_1$
singularity are given in (2.9). Finally, in 2.4, we provide the local equation of (an example of) a local deformation of a singularity of type
![]() $T_1$
to a node on the general fibre.
$T_1$
to a node on the general fibre.
The central part of our paper is Section 3. First of all, we prove in Lemma 3.2 that the only singularity of a surface
![]() $S_t\subset \mathcal {X}_t$
to which a singularity of type
$S_t\subset \mathcal {X}_t$
to which a singularity of type
![]() $T_1$
of a surface
$T_1$
of a surface
![]() $\mathcal S_0\subset \mathcal {X}_0$
may be deformed is a node. In §3.2.2, we describe the first-order locally trivial deformations in
$\mathcal S_0\subset \mathcal {X}_0$
may be deformed is a node. In §3.2.2, we describe the first-order locally trivial deformations in
![]() $\mathcal {X}_0$
of surfaces
$\mathcal {X}_0$
of surfaces
![]() $S_0=S_A\cup S_B$
with
$S_0=S_A\cup S_B$
with
![]() $T_1$
singularities on R and at most nodes elsewhere. In particular, we find sufficient conditions for smoothness of the equisingular deformation locus of
$T_1$
singularities on R and at most nodes elsewhere. In particular, we find sufficient conditions for smoothness of the equisingular deformation locus of
![]() $S_0$
in the relative Hilbert scheme of
$S_0$
in the relative Hilbert scheme of
![]() $\mathcal {X}$
. If these conditions are verified, then the
$\mathcal {X}$
. If these conditions are verified, then the
![]() $T_1$
singularities of
$T_1$
singularities of
![]() $S_0$
and its nodes can be smoothed independently inside
$S_0$
and its nodes can be smoothed independently inside
![]() $\mathcal {X}_0$
. Next, in §3.2.3, we consider deformations of a surface
$\mathcal {X}_0$
. Next, in §3.2.3, we consider deformations of a surface
![]() $S_0\subset \mathcal {X}_0$
, with
$S_0\subset \mathcal {X}_0$
, with
![]() $T_1$
singularities on R and at most nodes elsewhere, off the central fibre. We prove, in Theorem 3.13, that under suitable conditions, one can deform
$T_1$
singularities on R and at most nodes elsewhere, off the central fibre. We prove, in Theorem 3.13, that under suitable conditions, one can deform
![]() $S_0$
off the central fibre
$S_0$
off the central fibre
![]() $\mathcal {X}_0$
to a surface
$\mathcal {X}_0$
to a surface
![]() $S_t$
in the general fibre
$S_t$
in the general fibre
![]() $\mathcal {X}_t$
, with only nodes that are the deformations of the nodes of
$\mathcal {X}_t$
, with only nodes that are the deformations of the nodes of
![]() $S_0$
and of the
$S_0$
and of the
![]() $T_1$
singularites of
$T_1$
singularites of
![]() $S_0$
, and that the space of this deformation is generically smooth of the expected dimension. Again, generic smoothness means that the nodes of the general surface
$S_0$
, and that the space of this deformation is generically smooth of the expected dimension. Again, generic smoothness means that the nodes of the general surface
![]() $S_t$
can be independently smoothed.
$S_t$
can be independently smoothed.
In Section 4, we give a couple of applications of our general result. Essentially, we consider the following problem (see Problem 4.3). Let X be a smooth irreducible projective complex threefold. Let L be a line bundle on X such that the general surface in the linear system
![]() $| L|$
is smooth and irreducible. Let
$| L|$
is smooth and irreducible. Let
![]() $V^{X, |L|}_\delta $
be the Severi variety of surfaces S in
$V^{X, |L|}_\delta $
be the Severi variety of surfaces S in
![]() $|L|$
which are reduced with only
$|L|$
which are reduced with only
![]() $\delta $
nodes as singularities. The question we consider is as follows: Given X and L as above, which is the maximal value of
$\delta $
nodes as singularities. The question we consider is as follows: Given X and L as above, which is the maximal value of
![]() $\delta $
such that
$\delta $
such that
![]() $V^{X, |L|}_\delta $
has a generically smooth component of the expected codimension
$V^{X, |L|}_\delta $
has a generically smooth component of the expected codimension
![]() $\delta $
in
$\delta $
in
![]() $|L|$
? We give contributions to this problem in two cases. The first one is for
$|L|$
? We give contributions to this problem in two cases. The first one is for
![]() $X=\mathbb {P}^3$
and
$X=\mathbb {P}^3$
and
![]() $L=\mathcal {O}_{\mathbb {P}^3}(d)$
(see Theorem 4.6); the second one is when X is a general hypersurface of degree
$L=\mathcal {O}_{\mathbb {P}^3}(d)$
(see Theorem 4.6); the second one is when X is a general hypersurface of degree
![]() $h\geqslant 2$
in
$h\geqslant 2$
in
![]() $\mathbb {P}^4$
and
$\mathbb {P}^4$
and
![]() $L= \mathcal {O}_X(d)$
with
$L= \mathcal {O}_X(d)$
with
![]() $d\geqslant h-1$
(see Theorem 4.9).
$d\geqslant h-1$
(see Theorem 4.9).
To finish this introduction, it is worth mentioning that the basic idea of a singularity of type
![]() $T_1$
being a limit of a node is already contained, although in a rather obscure form, in B. Segre’s paper [Reference Segre18]. In this paper, Segre considers, even more generally, the case of higher dimension. As a matter of fact, we believe that there should be no obstruction in extending our results in higher dimension too. However, we did not dwell on this here because we thought that the surface in threefold case already shows the complexity of the situation. We plan to come back on this in the future.
$T_1$
being a limit of a node is already contained, although in a rather obscure form, in B. Segre’s paper [Reference Segre18]. In this paper, Segre considers, even more generally, the case of higher dimension. As a matter of fact, we believe that there should be no obstruction in extending our results in higher dimension too. However, we did not dwell on this here because we thought that the surface in threefold case already shows the complexity of the situation. We plan to come back on this in the future.
Notation: In what follows, we use standard notation in algebraic geometry. In particular, we will denote by
![]() $\sim $
the linear equivalence.
$\sim $
the linear equivalence.
2. Limit singularity of a node of a surface in a threefold
2.1. The problem
Let
![]() $\mathcal {X}\to \mathbb {D}$
be a flat family of projective complex 3-folds over a disc
$\mathcal {X}\to \mathbb {D}$
be a flat family of projective complex 3-folds over a disc
![]() $\mathbb {D}$
with smooth total space
$\mathbb {D}$
with smooth total space
![]() $\mathcal {X}$
and smooth general fiber
$\mathcal {X}$
and smooth general fiber
![]() $\mathcal {X}_t$
, with
$\mathcal {X}_t$
, with
![]() $t \in \mathbb {D}\setminus \{0\}$
, and whose special fiber
$t \in \mathbb {D}\setminus \{0\}$
, and whose special fiber
![]() $\mathcal {X}_0$
has double normal crossing singularities; in particular,
$\mathcal {X}_0$
has double normal crossing singularities; in particular,
![]() $\mathcal {X}_0=A\cup B$
has two smooth irreducible components A and B, intersecting transversally along a smooth surface
$\mathcal {X}_0=A\cup B$
has two smooth irreducible components A and B, intersecting transversally along a smooth surface
![]() $R=A\cap B.$
$R=A\cap B.$
Let
![]() $\mathcal L$
be a line bundle on
$\mathcal L$
be a line bundle on
![]() $\mathcal {X}$
. For each
$\mathcal {X}$
. For each
![]() $t\in \mathbb {D}$
, we set
$t\in \mathbb {D}$
, we set
![]() $\mathcal L_t= \mathcal L_{| \mathcal {X}_t}$
. We consider the following question. Roughly speaking, assume that for
$\mathcal L_t= \mathcal L_{| \mathcal {X}_t}$
. We consider the following question. Roughly speaking, assume that for
![]() $t\in \mathbb {D}$
general, we have a surface
$t\in \mathbb {D}$
general, we have a surface
![]() $S_t\in |\mathcal L_t|$
having a double point
$S_t\in |\mathcal L_t|$
having a double point
![]() $p_t$
. Assume that
$p_t$
. Assume that
![]() $S_t$
tends to a surface
$S_t$
tends to a surface
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
with
$\mathcal {X}_0$
with
![]() $p_t$
tending to a point
$p_t$
tending to a point
![]() $p_0\in R$
. The question is: What is the singularity that
$p_0\in R$
. The question is: What is the singularity that
![]() $S_0$
has at
$S_0$
has at
![]() $p_0$
? Let us make this setting more precise.
$p_0$
? Let us make this setting more precise.
2.2. Set up
Let us fix
![]() $p=p_0\in R$
, which is a double point for the central fibre
$p=p_0\in R$
, which is a double point for the central fibre
![]() $\mathcal {X}_0$
, whereas
$\mathcal {X}_0$
, whereas
![]() $\mathcal {X}$
is smooth at p. Hence, there are no sections of
$\mathcal {X}$
is smooth at p. Hence, there are no sections of
![]() $\mathcal {X}\to \mathbb {D}$
passing through p. So let us consider a smooth bisection
$\mathcal {X}\to \mathbb {D}$
passing through p. So let us consider a smooth bisection
![]() $\gamma ^\prime $
of
$\gamma ^\prime $
of
![]() $\mathcal {X}\to \mathbb {D}$
passing through p.
$\mathcal {X}\to \mathbb {D}$
passing through p.
Step 0. Let us look at the following commutative diagram:

where the rightmost square is cartesian and
![]() $\nu _2: u\in \mathbb {D}\to u^2\in \mathbb {D}$
. Then
$\nu _2: u\in \mathbb {D}\to u^2\in \mathbb {D}$
. Then
![]() $\mathcal {X}'$
is singular along the counterimage of R (that by abuse of notation, we still denote by R), which is a locus of double points for
$\mathcal {X}'$
is singular along the counterimage of R (that by abuse of notation, we still denote by R), which is a locus of double points for
![]() $\mathcal {X}'$
, with tangent cone a quadric cone of rank 3. The morphism
$\mathcal {X}'$
, with tangent cone a quadric cone of rank 3. The morphism
![]() $\mathcal Y\to \mathcal {X}'$
is the desingularization of
$\mathcal Y\to \mathcal {X}'$
is the desingularization of
![]() $\mathcal {X}'$
obtained by blowing up
$\mathcal {X}'$
obtained by blowing up
![]() $\mathcal {X}'$
along R.
$\mathcal {X}'$
along R.
The induced morphism
![]() $\pi :\mathcal Y\to \mathcal {X}$
is
$\pi :\mathcal Y\to \mathcal {X}$
is
![]() $2:1$
outside the central fibre of
$2:1$
outside the central fibre of
![]() $\mathcal Y$
. In particular, for every
$\mathcal Y$
. In particular, for every
![]() $t\neq 0$
, there are exactly two fibres
$t\neq 0$
, there are exactly two fibres
![]() $\mathcal Y_{u_1}$
and
$\mathcal Y_{u_1}$
and
![]() $\mathcal Y_{u_2}$
of
$\mathcal Y_{u_2}$
of
![]() $\mathcal Y\to \mathbb {D}$
isomorphic to the fibre
$\mathcal Y\to \mathbb {D}$
isomorphic to the fibre
![]() $\mathcal {X}_t$
of
$\mathcal {X}_t$
of
![]() $\mathcal {X}\to \mathbb {D}$
via
$\mathcal {X}\to \mathbb {D}$
via
![]() $\pi $
, where
$\pi $
, where
![]() $\{u_1,\,u_2\}=\nu _2^{-1}(t)$
. The family
$\{u_1,\,u_2\}=\nu _2^{-1}(t)$
. The family
![]() $\mathcal Y\to \mathbb {D}$
has central fibre
$\mathcal Y\to \mathbb {D}$
has central fibre
![]() $\mathcal Y_0=A\cup \mathcal E\cup B$
, where, by abusing notation, A and B denote the proper transforms of A and B and
$\mathcal Y_0=A\cup \mathcal E\cup B$
, where, by abusing notation, A and B denote the proper transforms of A and B and
![]() $\mathcal E\to R$
is a
$\mathcal E\to R$
is a
![]() $\mathbb {P}^1$
-bundle on
$\mathbb {P}^1$
-bundle on
![]() $R.$
The morphism
$R.$
The morphism
![]() $\pi $
is totally ramified along A and B, and it contracts
$\pi $
is totally ramified along A and B, and it contracts
![]() $\mathcal E$
to R in
$\mathcal E$
to R in
![]() $\mathcal {X}$
. In particular,
$\mathcal {X}$
. In particular,
![]() $A\cap \mathcal E$
and
$A\cap \mathcal E$
and
![]() $B\cap \mathcal E$
are two non-intersecting sections of
$B\cap \mathcal E$
are two non-intersecting sections of
![]() $\mathcal E$
both isomorphic to R. Denote by F the fibre of
$\mathcal E$
both isomorphic to R. Denote by F the fibre of
![]() $\mathcal E\to R$
over the point
$\mathcal E\to R$
over the point
![]() $p\in R\subset \mathcal {X}_0$
. One has
$p\in R\subset \mathcal {X}_0$
. One has
![]() $F\cong \mathbb {P}^1$
. Now the counterimage of
$F\cong \mathbb {P}^1$
. Now the counterimage of
![]() $\gamma ^\prime $
on
$\gamma ^\prime $
on
![]() $\mathcal Y$
is the union of two sections of
$\mathcal Y$
is the union of two sections of
![]() $\mathcal Y\to \mathbb {D}$
, each intersecting
$\mathcal Y\to \mathbb {D}$
, each intersecting
![]() $\mathcal Y_0$
at a smooth point on F. We let
$\mathcal Y_0$
at a smooth point on F. We let
![]() $\gamma $
be one of these two sections and q be the intersection point of
$\gamma $
be one of these two sections and q be the intersection point of
![]() $\gamma $
and F.
$\gamma $
and F.
Assume there exists an effective divisor
![]() $\mathcal S\subset \mathcal Y$
, with
$\mathcal S\subset \mathcal Y$
, with
![]() $\mathcal S\sim \pi ^{*}(\mathcal L)$
, having double points along
$\mathcal S\sim \pi ^{*}(\mathcal L)$
, having double points along
![]() $\gamma .$
Let S be the image of
$\gamma .$
Let S be the image of
![]() $\mathcal S$
in
$\mathcal S$
in
![]() $\mathcal {X}$
via the morphism
$\mathcal {X}$
via the morphism
![]() $\pi $
. Note that S has points of multiplicity
$\pi $
. Note that S has points of multiplicity
![]() $2$
along the bisection
$2$
along the bisection
![]() $\gamma '$
. For every
$\gamma '$
. For every
![]() $t\neq 0$
, if
$t\neq 0$
, if
![]() $\mathcal Y_{u_1}$
and
$\mathcal Y_{u_1}$
and
![]() $\mathcal Y_{u_2}$
, with
$\mathcal Y_{u_2}$
, with
![]() $u_1^2=u_2^2=t$
, are the two fibres of
$u_1^2=u_2^2=t$
, are the two fibres of
![]() $\mathcal Y\to \mathbb {D}$
isomorphic to
$\mathcal Y\to \mathbb {D}$
isomorphic to
![]() $\mathcal {X}_t$
via
$\mathcal {X}_t$
via
![]() $\pi $
, we have
$\pi $
, we have
where
![]() $S_{u_i}=\pi (\mathcal S_{u_i})$
and
$S_{u_i}=\pi (\mathcal S_{u_i})$
and
![]() $\mathcal S_{u_i}=\mathcal S\cap \mathcal Y_{u_i}$
, for
$\mathcal S_{u_i}=\mathcal S\cap \mathcal Y_{u_i}$
, for
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $t=0$
, we have that
$t=0$
, we have that
where
![]() $S_A=\pi (\mathcal S\cap A)\subset A$
and
$S_A=\pi (\mathcal S\cap A)\subset A$
and
![]() $S_B=\pi (\mathcal S \cap B)\subset B$
.
$S_B=\pi (\mathcal S \cap B)\subset B$
.
We want to understand
![]() $S|_{\mathcal {X}_0}.$
To do this, we will first understand
$S|_{\mathcal {X}_0}.$
To do this, we will first understand
![]() $\mathcal S|_{\mathcal Y_0}.$
$\mathcal S|_{\mathcal Y_0}.$
Step 1.
Let
![]() $\pi _1:\mathcal Y^1\to \mathcal Y$
be the blowing-up of
$\pi _1:\mathcal Y^1\to \mathcal Y$
be the blowing-up of
![]() $\mathcal Y$
along
$\mathcal Y$
along
![]() $\gamma $
with exceptional divisor
$\gamma $
with exceptional divisor
![]() $\Gamma $
. We have a new family
$\Gamma $
. We have a new family
![]() $\mathcal Y^1\to \mathbb {D}$
with general fibre the blow up of
$\mathcal Y^1\to \mathbb {D}$
with general fibre the blow up of
![]() $ \mathcal Y_u\cong \mathcal {X}_{\nu _2(u)}$
at its intersection point with
$ \mathcal Y_u\cong \mathcal {X}_{\nu _2(u)}$
at its intersection point with
![]() $\gamma $
(that is also the point of multiplicity
$\gamma $
(that is also the point of multiplicity
![]() $2$
of the surface
$2$
of the surface
![]() $\mathcal S_u$
), and central fibre
$\mathcal S_u$
), and central fibre
![]() $\mathcal Y^1_0=A\cup \mathcal E^\prime \cup B,$
where
$\mathcal Y^1_0=A\cup \mathcal E^\prime \cup B,$
where
![]() $\mathcal E^\prime $
is the blow-up of
$\mathcal E^\prime $
is the blow-up of
![]() $\mathcal E$
at
$\mathcal E$
at
![]() $q.$
Still denoting by F the proper transform of F in
$q.$
Still denoting by F the proper transform of F in
![]() $\mathcal Y^1,$
we have that the proper transform
$\mathcal Y^1,$
we have that the proper transform
![]() $\mathcal S^1$
of
$\mathcal S^1$
of
![]() $\mathcal S$
in
$\mathcal S$
in
![]() $\mathcal Y^1$
satisfies
$\mathcal Y^1$
satisfies
We deduce that
![]() $\mathcal S^1 \cdot F=-2$
and hence
$\mathcal S^1 \cdot F=-2$
and hence
![]() $F\subset \mathcal S^1.$
$F\subset \mathcal S^1.$
Step 2.
Let now
![]() $\pi _2:\mathcal Y^2\to \mathcal Y^1$
be the blow-up of
$\pi _2:\mathcal Y^2\to \mathcal Y^1$
be the blow-up of
![]() $\mathcal Y^1$
along F with new exceptional divisor
$\mathcal Y^1$
along F with new exceptional divisor
![]() $\Theta $
. We have the new family
$\Theta $
. We have the new family
![]() $\mathcal Y^2\to \mathbb {D}$
, whose general fibre is the same as the general fibre of
$\mathcal Y^2\to \mathbb {D}$
, whose general fibre is the same as the general fibre of
![]() $\mathcal Y^1\to \mathbb {D}$
, and new central fibre
$\mathcal Y^1\to \mathbb {D}$
, and new central fibre
![]() $\mathcal Y^2_0=A^\prime \cup \mathcal E^{\prime \prime }\cup \Theta \cup B^\prime ,$
where
$\mathcal Y^2_0=A^\prime \cup \mathcal E^{\prime \prime }\cup \Theta \cup B^\prime ,$
where
![]() $A^\prime ,\,\mathcal E^{\prime \prime }$
and
$A^\prime ,\,\mathcal E^{\prime \prime }$
and
![]() $B^\prime $
are the blow-ups of
$B^\prime $
are the blow-ups of
![]() $A,\,\mathcal E^{\prime }$
and B at
$A,\,\mathcal E^{\prime }$
and B at
![]() $F\cap A$
,
$F\cap A$
,
![]() $F\subset \mathcal E^\prime $
and
$F\subset \mathcal E^\prime $
and
![]() $B\cap F$
, respectively. Notice that
$B\cap F$
, respectively. Notice that
![]() $\Theta \to F$
is a
$\Theta \to F$
is a
![]() $\mathbb {P}^2$
-bundle on F, intersecting
$\mathbb {P}^2$
-bundle on F, intersecting
![]() $A^\prime $
(resp.
$A^\prime $
(resp.
![]() $B^\prime $
) along a surface isomorphic to
$B^\prime $
) along a surface isomorphic to
![]() $\mathbb {P}^2$
, which is a fibre of
$\mathbb {P}^2$
, which is a fibre of
![]() $\Theta \to F$
, and at the same time is the exceptional divisor of the blow-up
$\Theta \to F$
, and at the same time is the exceptional divisor of the blow-up
![]() $A^\prime \to A$
at
$A^\prime \to A$
at
![]() $F\cap A$
(resp. of the blow-up
$F\cap A$
(resp. of the blow-up
![]() $B^\prime \to B$
at
$B^\prime \to B$
at
![]() $F\cap B$
). Moreover, the surface
$F\cap B$
). Moreover, the surface
![]() $E:=\Theta \cap \mathcal E^{\prime \prime }$
has a
$E:=\Theta \cap \mathcal E^{\prime \prime }$
has a
![]() $\mathbb {P}^1$
-bundle structure
$\mathbb {P}^1$
-bundle structure
![]() $E\to F$
, and it is the exceptional divisor of
$E\to F$
, and it is the exceptional divisor of
![]() $\mathcal E^{\prime \prime }$
, arising from the blowing-up of F in
$\mathcal E^{\prime \prime }$
, arising from the blowing-up of F in
![]() $\mathcal E^{\prime }$
.
$\mathcal E^{\prime }$
.
We claim that
![]() $E\simeq \mathbb {F}_0.$
Indeed, since
$E\simeq \mathbb {F}_0.$
Indeed, since
![]() $F\simeq \mathbb {P}^1$
and F is a fibre of
$F\simeq \mathbb {P}^1$
and F is a fibre of
![]() $\mathcal E\to R$
, we have that
$\mathcal E\to R$
, we have that
![]() $\mathcal N_{F|\mathcal E}\simeq \mathcal {O}_{\mathbb {P}^1}\oplus \mathcal {O}_{\mathbb {P}^1}$
. This implies that
$\mathcal N_{F|\mathcal E}\simeq \mathcal {O}_{\mathbb {P}^1}\oplus \mathcal {O}_{\mathbb {P}^1}$
. This implies that
![]() $\mathcal N_{F|\mathcal E'}=\mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}(-1),$
and hence,
$\mathcal N_{F|\mathcal E'}=\mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}(-1),$
and hence,
![]() $E=\mathbb {P}(\mathcal N_{F|\mathcal E'})=\mathbb {F}_0.$
$E=\mathbb {P}(\mathcal N_{F|\mathcal E'})=\mathbb {F}_0.$
If
![]() $\mathcal S^2$
is the proper transform of
$\mathcal S^2$
is the proper transform of
![]() $\mathcal S^1$
in
$\mathcal S^1$
in
![]() $\mathcal Y^2,$
by (2.1), we deduce that
$\mathcal Y^2,$
by (2.1), we deduce that
 $$ \begin{align} \mathcal S^2|_{\Theta} &\sim \pi^{*}_2(\mathcal S^1)|_{\Theta}-m_F\Theta|_{\Theta} \nonumber\\ &\sim- 2 f_\Theta+m_F(A^\prime+B^\prime+\mathcal E^{\prime\prime})|_{\Theta} \nonumber\\ &\sim - 2 f_\Theta+m_F(2f_\Theta+ \mathcal E^{\prime\prime}|_\Theta) \nonumber\\ &\sim (2m_F- 2 )f_\Theta+m_F( \mathcal E^{\prime\prime}|_\Theta)\nonumber\\ &\sim (2m_F- 2 )f_\Theta+m_FE, \end{align} $$
$$ \begin{align} \mathcal S^2|_{\Theta} &\sim \pi^{*}_2(\mathcal S^1)|_{\Theta}-m_F\Theta|_{\Theta} \nonumber\\ &\sim- 2 f_\Theta+m_F(A^\prime+B^\prime+\mathcal E^{\prime\prime})|_{\Theta} \nonumber\\ &\sim - 2 f_\Theta+m_F(2f_\Theta+ \mathcal E^{\prime\prime}|_\Theta) \nonumber\\ &\sim (2m_F- 2 )f_\Theta+m_F( \mathcal E^{\prime\prime}|_\Theta)\nonumber\\ &\sim (2m_F- 2 )f_\Theta+m_FE, \end{align} $$
where
![]() $f_\Theta $
denotes the linear equivalence class of a fibre of
$f_\Theta $
denotes the linear equivalence class of a fibre of
![]() $\Theta \to F$
and
$\Theta \to F$
and
![]() $m_F$
is the multiplicity of
$m_F$
is the multiplicity of
![]() $\mathcal S^1$
along
$\mathcal S^1$
along
![]() $F.$
Notice that
$F.$
Notice that
![]() $\mathcal S^2|_{\Theta }$
must be an effective divisor because it is the restriction to
$\mathcal S^2|_{\Theta }$
must be an effective divisor because it is the restriction to
![]() $\Theta $
of an effective divisor that does not contain
$\Theta $
of an effective divisor that does not contain
![]() $\Theta $
. This implies the minimum value of
$\Theta $
. This implies the minimum value of
![]() $m_F$
making
$m_F$
making
![]() $\mathcal S^2|_{\Theta }$
effective is
$\mathcal S^2|_{\Theta }$
effective is
![]() $m_F=1$
.
$m_F=1$
.
2.3. Description of
 $\mathcal S_{|\mathcal Y_0}$
and of
$\mathcal S_{|\mathcal Y_0}$
and of
 $S_{|\mathcal {X}_0}$
$S_{|\mathcal {X}_0}$
We assume now
![]() $m_F=1$
. To better understand
$m_F=1$
. To better understand
![]() $\mathcal S^2|_{\Theta }\sim E$
, we restrict
$\mathcal S^2|_{\Theta }\sim E$
, we restrict
![]() $\mathcal S^2|_{\Theta }$
to
$\mathcal S^2|_{\Theta }$
to
![]() $\mathcal E"$
. Let
$\mathcal E"$
. Let
![]() $\sigma $
and f, with
$\sigma $
and f, with
![]() $\sigma ^2=f^2=0$
, be the generators of the Picard group of
$\sigma ^2=f^2=0$
, be the generators of the Picard group of
![]() $E=\mathcal E"\cap \Theta \cong \mathbb {F}_0$
. By restricting (2.2) to E, one gets
$E=\mathcal E"\cap \Theta \cong \mathbb {F}_0$
. By restricting (2.2) to E, one gets
To compute
![]() $\mathcal E^{\prime \prime }_{|E}$
, we use the obvious relation
$\mathcal E^{\prime \prime }_{|E}$
, we use the obvious relation
![]() $( A'+B' +\Theta +\mathcal E")_{|E}=0$
, which implies the following identity on E:
$( A'+B' +\Theta +\mathcal E")_{|E}=0$
, which implies the following identity on E:
Since
![]() $E=\mathcal E"\cap \Theta $
, then
$E=\mathcal E"\cap \Theta $
, then
![]() $\Theta _{|E}$
is the class of
$\Theta _{|E}$
is the class of
![]() $\Theta ^2\cdot \mathcal E^{\prime \prime }$
which is clearly the class of the normal bundle
$\Theta ^2\cdot \mathcal E^{\prime \prime }$
which is clearly the class of the normal bundle
![]() $\mathcal N_{E|\mathcal E"}$
of E in
$\mathcal N_{E|\mathcal E"}$
of E in
![]() $\mathcal E^{\prime \prime }$
. Similarly,
$\mathcal E^{\prime \prime }$
. Similarly,
![]() $\mathcal E^{\prime \prime }_{|E}$
is the class of
$\mathcal E^{\prime \prime }_{|E}$
is the class of
![]() $\Theta \cdot {\mathcal E^{\prime \prime }}^2=c_1(\mathcal N_{E|\Theta })$
. Since
$\Theta \cdot {\mathcal E^{\prime \prime }}^2=c_1(\mathcal N_{E|\Theta })$
. Since
![]() $E=\mathbb {P}(\mathcal N_{F|\mathcal E'})$
, denoting by
$E=\mathbb {P}(\mathcal N_{F|\mathcal E'})$
, denoting by
![]() $\pi _E:E\to F$
the natural projection morphism, whose fiber is f, and by
$\pi _E:E\to F$
the natural projection morphism, whose fiber is f, and by
we have that
![]() $\mathcal N_{E|\mathcal E"}\subset \pi _E^{*}(\mathcal N_{F|\mathcal E'})$
is the tautological fibre bundle of
$\mathcal N_{E|\mathcal E"}\subset \pi _E^{*}(\mathcal N_{F|\mathcal E'})$
is the tautological fibre bundle of
![]() $E=\mathbb {P}(\mathcal N_{F|\mathcal E'})$
. So we get that
$E=\mathbb {P}(\mathcal N_{F|\mathcal E'})$
. So we get that
and
(see [Reference Griffiths and Harris12, p. 606]). Now
since
![]() $\mathcal N_{F|\mathcal E'}$
is a vector bundle on F and
$\mathcal N_{F|\mathcal E'}$
is a vector bundle on F and
![]() $\dim (F)=1.$
So
$\dim (F)=1.$
So
Thus,
Set
![]() $e=a\sigma +b f$
. By (2.5) and (2.6), one gets
$e=a\sigma +b f$
. By (2.5) and (2.6), one gets
![]() $a=-1$
and
$a=-1$
and
Thus, we have
Hence, by (2.4), we get
Remark 2.1. From (2.7), it follows that the divisor E (which does not move on
![]() $\mathcal E"$
being there an exceptional divisor) does not move in
$\mathcal E"$
being there an exceptional divisor) does not move in
![]() $\Theta $
either, since
$\Theta $
either, since
![]() $\mathcal N_{E| \Theta }$
is non-effective. Hence, by (2.2) and
$\mathcal N_{E| \Theta }$
is non-effective. Hence, by (2.2) and
![]() $m_F=1$
, we have
$m_F=1$
, we have
![]() $\mathcal S^2|_E=E$
.
$\mathcal S^2|_E=E$
.
We are now also able to describe the divisor
![]() $\mathcal S^2|_{A'\cap \mathcal E"}\cong \mathcal S^2|_{B'\cap \mathcal E"}$
. Indeed,
$\mathcal S^2|_{A'\cap \mathcal E"}\cong \mathcal S^2|_{B'\cap \mathcal E"}$
. Indeed,
and, since
![]() $\mathcal S^2|_\Theta =E$
by Remark 2.1, it contains the
$\mathcal S^2|_\Theta =E$
by Remark 2.1, it contains the
![]() $(-1)$
-curve
$(-1)$
-curve
![]() $ \Theta \cap A'\cap \mathcal E"=E\cap A'$
in its base locus with multiplicity
$ \Theta \cap A'\cap \mathcal E"=E\cap A'$
in its base locus with multiplicity
![]() $1$
. Thus,
$1$
. Thus,
![]() $ \mathcal S^2|_{A'\cap \mathcal E"} = \mathcal D_A\cup (\Theta \cap A'\cap \mathcal E"), $
where
$ \mathcal S^2|_{A'\cap \mathcal E"} = \mathcal D_A\cup (\Theta \cap A'\cap \mathcal E"), $
where
and similarly for
![]() $\mathcal S^2|_{B'\cap \mathcal E"}.$
$\mathcal S^2|_{B'\cap \mathcal E"}.$
This analysis implies the following:
Theorem 2.2. Let
![]() $\mathcal S\subset \mathcal Y$
be an effective Cartier divisor as in Step 0. Then the surface
$\mathcal S\subset \mathcal Y$
be an effective Cartier divisor as in Step 0. Then the surface
![]() $\mathcal S_{|\mathcal Y_0}$
is the union of three surfaces
$\mathcal S_{|\mathcal Y_0}$
is the union of three surfaces
![]() $\mathcal S_A=\mathcal S\cap A, \mathcal S_B=\mathcal S\cap B$
and
$\mathcal S_A=\mathcal S\cap A, \mathcal S_B=\mathcal S\cap B$
and
![]() $\mathcal S_{\mathcal E}=\mathcal S\cap \mathcal E$
, where
$\mathcal S_{\mathcal E}=\mathcal S\cap \mathcal E$
, where
![]() $\mathcal S_A$
(resp.
$\mathcal S_A$
(resp.
![]() $ \mathcal S_B$
) intersects
$ \mathcal S_B$
) intersects
![]() $A\cap \mathcal E$
(resp.
$A\cap \mathcal E$
(resp.
![]() $B\cap \mathcal E$
) along a curve which has a double point at the point
$B\cap \mathcal E$
) along a curve which has a double point at the point
![]() $F\cap A$
(resp.
$F\cap A$
(resp.
![]() $F\cap B$
), these two curves are isomorphic, and
$F\cap B$
), these two curves are isomorphic, and
![]() $\mathcal S_{\mathcal E}$
is a
$\mathcal S_{\mathcal E}$
is a
![]() $\mathbb {P}^1$
-bundle over any one of them.
$\mathbb {P}^1$
-bundle over any one of them.
Accordingly,
![]() $S_{|\mathcal {X}_0}=2S_0$
, with
$S_{|\mathcal {X}_0}=2S_0$
, with
![]() $S_0\in |\mathcal L_0|$
and
$S_0\in |\mathcal L_0|$
and
![]() $S_0$
is the union of two surfaces
$S_0$
is the union of two surfaces
![]() $S_A$
,
$S_A$
,
![]() $S_B$
, respectively isomorphic to
$S_B$
, respectively isomorphic to
![]() $\mathcal S_A, \mathcal S_B$
, intersecting along a curve in R that has a double point at p (see Figure 1).
$\mathcal S_A, \mathcal S_B$
, intersecting along a curve in R that has a double point at p (see Figure 1).

Figure 1 A
![]() $T_1$
-singularity of a surface
$T_1$
-singularity of a surface
![]() $S_0=S_A\cup S_B$
in
$S_0=S_A\cup S_B$
in
![]() $\mathcal X_0=A\cup B$
.
$\mathcal X_0=A\cup B$
.
2.3.1. Local equations of
 $S_0$
$S_0$
We may assume that
![]() $\mathcal {X}$
locally around
$\mathcal {X}$
locally around
![]() $p\in \mathcal {X}_0$
is embedded in
$p\in \mathcal {X}_0$
is embedded in
![]() $\mathbb {A}^5$
with coordinates
$\mathbb {A}^5$
with coordinates
![]() $(x,y,z,u,t)$
with p corresponding to the origin. We may suppose that
$(x,y,z,u,t)$
with p corresponding to the origin. We may suppose that
![]() $\mathcal {X}$
is defined by the equation
$\mathcal {X}$
is defined by the equation
![]() $xy=t$
and the map
$xy=t$
and the map
![]() $\mathcal {X}\to \mathbb {D}$
is given by
$\mathcal {X}\to \mathbb {D}$
is given by
![]() $(x,y,z,u,t)\mapsto t$
. So we will assume that A is defined by the equations
$(x,y,z,u,t)\mapsto t$
. So we will assume that A is defined by the equations
![]() $x=t=0$
and B by the equations
$x=t=0$
and B by the equations
![]() $y=t=0$
, so that R is defined by
$y=t=0$
, so that R is defined by
![]() $x=y=t=0$
.
$x=y=t=0$
.
The above analysis proves that the surfaces
![]() $\mathcal S|_A$
and
$\mathcal S|_A$
and
![]() $\mathcal S|_B$
belong to the restriction linear systems of
$\mathcal S|_B$
belong to the restriction linear systems of
![]() $\mathcal L$
to A and B, respectively, and moreover are tangent to R at the point p. Thus,
$\mathcal L$
to A and B, respectively, and moreover are tangent to R at the point p. Thus,
![]() $S_0=S_A\cup S_B$
belongs to the linear system
$S_0=S_A\cup S_B$
belongs to the linear system
![]() $\mathcal L_0(2,p)\subset |\mathcal L_0|$
of surfaces with local equations at p given by
$\mathcal L_0(2,p)\subset |\mathcal L_0|$
of surfaces with local equations at p given by
 $$ \begin{align} \left\{\begin{array}{l} (a_1x+b_1y)+f_2(x,y,z,u)=0\\ xy=0, \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{l} (a_1x+b_1y)+f_2(x,y,z,u)=0\\ xy=0, \end{array}\right. \end{align} $$
with
![]() $f_2(x,y,z,u)$
an analytic function with terms of degree at least
$f_2(x,y,z,u)$
an analytic function with terms of degree at least
![]() $2$
.
$2$
.
Definition 2.2.1. Let
![]() $S_0=S_A\cup S_B$
be a surface that is the union of two irreducible components
$S_0=S_A\cup S_B$
be a surface that is the union of two irreducible components
![]() $S_A,S_B$
intersecting along a curve C. Let
$S_A,S_B$
intersecting along a curve C. Let
![]() $p\in C$
. We will say that
$p\in C$
. We will say that
![]() $S_0$
has at p a singularity of type
$S_0$
has at p a singularity of type
![]() $T_1$
if
$T_1$
if
![]() $S_A$
and
$S_A$
and
![]() $S_B$
are smooth at p and C has at p a node.
$S_B$
are smooth at p and C has at p a node.
Remark 2.3. If in (2.8),
![]() $a_1b_1\neq 0$
, then
$a_1b_1\neq 0$
, then
![]() $S_0$
has a
$S_0$
has a
![]() $T_1$
singularity at the origin p, and, up to a linear change of coordinates, the local equations are given by
$T_1$
singularity at the origin p, and, up to a linear change of coordinates, the local equations are given by
 $$ \begin{align} \left\{\begin{array}{l} x+y+f_2(x,y,z,u)=0,\,\,\mathrm{{with}}\,\, f_2(0,0,z,u)=0\,\,\mathrm{{having\, a\, node\, at}}\,\,\underline 0,\\ xy=0.\,\, \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{l} x+y+f_2(x,y,z,u)=0,\,\,\mathrm{{with}}\,\, f_2(0,0,z,u)=0\,\,\mathrm{{having\, a\, node\, at}}\,\,\underline 0,\\ xy=0.\,\, \end{array}\right. \end{align} $$
In the sequel, we will also refer to
![]() $\mathcal L_0(2,p)$
as the sublinear system of
$\mathcal L_0(2,p)$
as the sublinear system of
![]() $|\mathcal L_0|$
of surfaces with at least a
$|\mathcal L_0|$
of surfaces with at least a
![]() $T_1$
singularity at
$T_1$
singularity at
![]() $p.$
$p.$
Remark 2.4. We have that
![]() $\mathcal L_0(2,p)\subset |\mathcal L_0|$
has dimension
$\mathcal L_0(2,p)\subset |\mathcal L_0|$
has dimension
2.4. Local deformation of a singularity of type
 $T_1$
to a node
$T_1$
to a node
In §2.3.1, we saw that a singularity of type
![]() $T_1$
appears as a generic limit of a double point of a surface. In this section, we will show that locally the converse happens, i.e., that locally a singularity of type
$T_1$
appears as a generic limit of a double point of a surface. In this section, we will show that locally the converse happens, i.e., that locally a singularity of type
![]() $T_1$
can be deformed to a node.
$T_1$
can be deformed to a node.
In local coordinates
![]() $(x,y,z,u,t)$
, we consider as before the family of
$(x,y,z,u,t)$
, we consider as before the family of
![]() $3$
-folds
$3$
-folds
![]() $\mathcal {X}_t:xy=t.$
We further consider the one parameter family of
$\mathcal {X}_t:xy=t.$
We further consider the one parameter family of
![]() $3$
-folds in
$3$
-folds in
![]() $\mathbb {A}^4$
of local equation at
$\mathbb {A}^4$
of local equation at
![]() $\underline 0$
given by
$\underline 0$
given by
where
![]() $\alpha (t)$
is a suitable function of
$\alpha (t)$
is a suitable function of
![]() $t\in \mathbb {A}^1$
to be determined, such that
$t\in \mathbb {A}^1$
to be determined, such that
![]() $\alpha (0)=0$
. We will set
$\alpha (0)=0$
. We will set
![]() $S_t=\mathcal S_{\alpha (t)}\cap \mathcal {X}_t$
for any
$S_t=\mathcal S_{\alpha (t)}\cap \mathcal {X}_t$
for any
![]() $t\in \mathbb {A}^1$
. The surface
$t\in \mathbb {A}^1$
. The surface
![]() $S_0$
has a
$S_0$
has a
![]() $T_1$
singularity at
$T_1$
singularity at
![]() $\underline 0$
and
$\underline 0$
and
![]() $\mathcal S_{\alpha }$
is smooth. Our requirement on the function
$\mathcal S_{\alpha }$
is smooth. Our requirement on the function
![]() $\alpha (t)$
is that for any
$\alpha (t)$
is that for any
![]() $t\neq 0$
, there exists a singular point
$t\neq 0$
, there exists a singular point
![]() $q(t)=(x(t),y(t),z(t),u(t))\in S_t$
, that is, such that
$q(t)=(x(t),y(t),z(t),u(t))\in S_t$
, that is, such that
This is equivalent to asking if there exists
![]() $q(t)=(x(t),y(t),z(t),u(t))\in \mathbb {A}^4$
satisfying
$q(t)=(x(t),y(t),z(t),u(t))\in \mathbb {A}^4$
satisfying
and
for a non-zero
![]() $c(t)$
. This implies
$c(t)$
. This implies
Thus, for every
![]() $t\neq 0$
, there exist exactly two divisors
$t\neq 0$
, there exist exactly two divisors
![]() $\mathcal S_{\alpha _i}$
, with
$\mathcal S_{\alpha _i}$
, with
![]() $i=1,2$
and
$i=1,2$
and
![]() $\alpha _i(t)^2=-4t$
so that
$\alpha _i(t)^2=-4t$
so that
 $$ \begin{align*} S_{\alpha_i(t)}=\mathcal S_{\alpha_i}\cap\mathcal Y_t: \left\{\begin{array}{l} x=y+\alpha_i(t)+z^2+u^2\\ y(y+\alpha_i(t)+z^2+u^2)=t \end{array}\right. \end{align*} $$
$$ \begin{align*} S_{\alpha_i(t)}=\mathcal S_{\alpha_i}\cap\mathcal Y_t: \left\{\begin{array}{l} x=y+\alpha_i(t)+z^2+u^2\\ y(y+\alpha_i(t)+z^2+u^2)=t \end{array}\right. \end{align*} $$
is a one-nodal surface, with tangent cone at
![]() $q_i(t)=(\frac {\alpha _i(t)}{2},-\frac {\alpha _i(t)}{2},0,0)$
given by
$q_i(t)=(\frac {\alpha _i(t)}{2},-\frac {\alpha _i(t)}{2},0,0)$
given by
Notice that, for every
![]() $i=1,2$
, we have that
$i=1,2$
, we have that
![]() $\alpha _i(t)$
is a well-defined continuous function on
$\alpha _i(t)$
is a well-defined continuous function on
![]() ${\mathbb {D}_\epsilon ^o=\mathbb {D}(\underline 0,\epsilon )\setminus \{a+i0\,|\, 0<a<\epsilon \}}$
(the disk cut along a radius), vanishing at
${\mathbb {D}_\epsilon ^o=\mathbb {D}(\underline 0,\epsilon )\setminus \{a+i0\,|\, 0<a<\epsilon \}}$
(the disk cut along a radius), vanishing at
![]() $0$
and holomorphic on
$0$
and holomorphic on
![]() $\mathbb {D}_\epsilon ^o\setminus \underline 0$
. Each family
$\mathbb {D}_\epsilon ^o\setminus \underline 0$
. Each family
![]() $\mathcal S_{\alpha _i}\to \mathbb {D}_{\epsilon }^o$
, for
$\mathcal S_{\alpha _i}\to \mathbb {D}_{\epsilon }^o$
, for
![]() $i=1,2$
, is not algebraic, while the complete intersection family of surfaces
$i=1,2$
, is not algebraic, while the complete intersection family of surfaces
 $$ \begin{align} \mathcal D: \left\{\begin{array}{l} (x-y-u^2-z^2)^2=-4t\\ xy=t. \end{array}\right. \end{align} $$
$$ \begin{align} \mathcal D: \left\{\begin{array}{l} (x-y-u^2-z^2)^2=-4t\\ xy=t. \end{array}\right. \end{align} $$
is algebraic. As usual, we set
![]() $D_t=\mathcal D\cap \mathcal {X}_t$
. One has
$D_t=\mathcal D\cap \mathcal {X}_t$
. One has
![]() $D_t=S_{\alpha _1(t)}\cup S_{\alpha _2(t)}$
for
$D_t=S_{\alpha _1(t)}\cup S_{\alpha _2(t)}$
for
![]() $t\neq 0$
and non-reduced fibre
$t\neq 0$
and non-reduced fibre
![]() $D_0=2S_0$
for
$D_0=2S_0$
for
![]() $t=0$
.
$t=0$
.
The locus
![]() $x^2+t=x+y=z=u=0$
, whose general point is singular for
$x^2+t=x+y=z=u=0$
, whose general point is singular for
![]() $D_t$
, is a bisection of
$D_t$
, is a bisection of
![]() $\mathcal {X}\to \mathbb {A}^1$
passing through
$\mathcal {X}\to \mathbb {A}^1$
passing through
![]() $(\underline 0,0)$
.
$(\underline 0,0)$
.
3. Deformations of surfaces with
 $T_1$
singularities and nodes
$T_1$
singularities and nodes
Throughout this section, we will consider
![]() $\mathcal {X}\to \mathbb {D}$
a family of projective complex 3-folds over a disc
$\mathcal {X}\to \mathbb {D}$
a family of projective complex 3-folds over a disc
![]() $\mathbb {D}$
as in the previous section, and we let
$\mathbb {D}$
as in the previous section, and we let
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
be its relative Hilbert scheme, whose fiber over
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
be its relative Hilbert scheme, whose fiber over
![]() $t\in \mathbb {D}$
is the Hilbert scheme of
$t\in \mathbb {D}$
is the Hilbert scheme of
![]() $\mathcal {X}_t$
and it is denoted by
$\mathcal {X}_t$
and it is denoted by
![]() $\mathcal H^{\mathcal {X}_t}$
. Moreover, we will consider
$\mathcal H^{\mathcal {X}_t}$
. Moreover, we will consider
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
![]() $S_A\subset A$
and
$S_A\subset A$
and
![]() $S_B\subset B$
an effective reduced Cartier divisor.
$S_B\subset B$
an effective reduced Cartier divisor.
3.1. Deformations and a smoothness criterion
Definition 3.0.1. Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
![]() $S_A\subset A$
and
$S_A\subset A$
and
![]() $S_B\subset B$
being an effective reduced Cartier divisor and let
$S_B\subset B$
being an effective reduced Cartier divisor and let
be an irreducible component of the relative Hilbert scheme of
![]() $\mathcal {X}$
containing
$\mathcal {X}$
containing
![]() $[S_0]$
. A deformation of
$[S_0]$
. A deformation of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
not in
$\mathcal {X}$
not in
![]() $\mathcal {X}_0$
is the total space
$\mathcal {X}_0$
is the total space
![]() $S\subset \mathcal {X}$
of an irreducible local r-multisection
$S\subset \mathcal {X}$
of an irreducible local r-multisection
![]() $\gamma $
of
$\gamma $
of
![]() $\mathcal H_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
passing through
$\mathcal H_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
passing through
![]() $[S_0]$
. Equivalently, a deformation of
$[S_0]$
. Equivalently, a deformation of
![]() $S_0$
is an effective divisor
$S_0$
is an effective divisor

dominating
![]() $\mathbb {D}$
, whose central fibre is
$\mathbb {D}$
, whose central fibre is
![]() $S\cap \mathcal {X}_0=rS_0$
(i.e., the surface
$S\cap \mathcal {X}_0=rS_0$
(i.e., the surface
![]() $S_0$
counted with multiplicity r) and whose general fibre is a reduced surface with r irreducible components
$S_0$
counted with multiplicity r) and whose general fibre is a reduced surface with r irreducible components
![]() $S\cap \mathcal {X}_t=S_t^1\cup \cdots \cup S_t^r$
, with
$S\cap \mathcal {X}_t=S_t^1\cup \cdots \cup S_t^r$
, with
![]() $[S_t^i]\in \mathcal H_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
, for every
$[S_t^i]\in \mathcal H_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
, for every
![]() $i=1,\ldots , t$
. We will also say that every irreducible component
$i=1,\ldots , t$
. We will also say that every irreducible component
![]() $S_t^i$
of
$S_t^i$
of
![]() $S\cap \mathcal {X}_t$
is a deformation of
$S\cap \mathcal {X}_t$
is a deformation of
![]() $S_0$
or that
$S_0$
or that
![]() $S_0$
is a limit of
$S_0$
is a limit of
![]() $S_t^i$
. Let
$S_t^i$
. Let
![]() $\mathcal Y$
be the smooth family of threefolds obtained from
$\mathcal Y$
be the smooth family of threefolds obtained from
![]() $\mathcal {X}\to \mathbb {D}$
after a base change
$\mathcal {X}\to \mathbb {D}$
after a base change

of order r and after minimally desingularizing the total space of the obtained family.
![]() $\mathcal Y$
has central fibre
$\mathcal Y$
has central fibre
![]() $\mathcal Y_0=A\cup \mathcal E_1\cup \dots \cup \mathcal E_{r-1}\cup B$
with normal crossing singularities of multiplicity two, where every
$\mathcal Y_0=A\cup \mathcal E_1\cup \dots \cup \mathcal E_{r-1}\cup B$
with normal crossing singularities of multiplicity two, where every
![]() $\mathcal E_i$
is a
$\mathcal E_i$
is a
![]() $\mathbb {P}^1$
-bundle over
$\mathbb {P}^1$
-bundle over
![]() $\mathcal E_{i-1}\cap \mathcal E_i$
, intersecting
$\mathcal E_{i-1}\cap \mathcal E_i$
, intersecting
![]() $\mathcal E_{i-1}$
and
$\mathcal E_{i-1}$
and
![]() $\mathcal E_{i+1}$
, with
$\mathcal E_{i+1}$
, with
![]() $\mathcal E_0=A$
and
$\mathcal E_0=A$
and
![]() $\mathcal E_{r}=B$
. We denote by
$\mathcal E_{r}=B$
. We denote by
![]() $\pi :\mathcal Y\to \mathcal {X}$
the induced morphism. Then the pullback divisor
$\pi :\mathcal Y\to \mathcal {X}$
the induced morphism. Then the pullback divisor
![]() $\pi ^{*}(S)=\mathcal S^1\cup \dots \cup \mathcal S^r$
has r irreducible distinct components
$\pi ^{*}(S)=\mathcal S^1\cup \dots \cup \mathcal S^r$
has r irreducible distinct components
![]() $\mathcal S^1,\dots , \mathcal S^r$
, where now every
$\mathcal S^1,\dots , \mathcal S^r$
, where now every
![]() $\mathcal S^i$
has irreducible general fibre and has central fibre given by
$\mathcal S^i$
has irreducible general fibre and has central fibre given by
![]() $\mathcal S^i_0=\mathcal S^i\cap \mathcal {X}_0\cong S_0$
.
$\mathcal S^i_0=\mathcal S^i\cap \mathcal {X}_0\cong S_0$
.
Proposition 3.1. Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
, with
![]() $S_A\subset A$
and
$S_A\subset A$
and
![]() $S_B\subset B$
, be a reduced effective Cartier divisor as above. Let p be a point of the intersection curve
$S_B\subset B$
, be a reduced effective Cartier divisor as above. Let p be a point of the intersection curve
![]() $C=S_A\cap S_B\subset R$
where
$C=S_A\cap S_B\subset R$
where
![]() $S_A$
and
$S_A$
and
![]() $S_B$
intersect transversally (i.e., such that
$S_B$
intersect transversally (i.e., such that
![]() $S_A$
and
$S_A$
and
![]() $S_B$
are smooth at p and
$S_B$
are smooth at p and
![]() $T_p(S_A)\neq T_p(S_B)).$
Then for every deformation
$T_p(S_A)\neq T_p(S_B)).$
Then for every deformation
![]() $S\subset \mathcal {X}$
of
$S\subset \mathcal {X}$
of
![]() $S_0$
not in
$S_0$
not in
![]() $\mathcal {X}_0$
, we have that p is limit only of smooth points of the irreducible components of the general fibre of S (i.e., in a sufficiently small analytic neighborhood of p in
$\mathcal {X}_0$
, we have that p is limit only of smooth points of the irreducible components of the general fibre of S (i.e., in a sufficiently small analytic neighborhood of p in
![]() $\mathcal {X}$
, all irreducible components of the general fibre of S are smooth). In particular, if
$\mathcal {X}$
, all irreducible components of the general fibre of S are smooth). In particular, if
![]() $S_A$
and
$S_A$
and
![]() $S_B$
intersect transversally along C, then
$S_B$
intersect transversally along C, then
![]() $S_0$
is limit only of smooth surfaces.
$S_0$
is limit only of smooth surfaces.
Proof. Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
and
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
and
![]() $p\in R=S_A\cap S_B$
as in the statement. Then, there exists an analytic coordinate system
$p\in R=S_A\cap S_B$
as in the statement. Then, there exists an analytic coordinate system
![]() $(x,y,z,u,t)$
of
$(x,y,z,u,t)$
of
![]() $\mathcal {X}$
at
$\mathcal {X}$
at
![]() $p=\underline 0$
and such that the local equation of
$p=\underline 0$
and such that the local equation of
![]() $S_0$
at p is given by
$S_0$
at p is given by
![]() $xy=t=z+f_2(x,y,z,u)=0$
, where
$xy=t=z+f_2(x,y,z,u)=0$
, where
![]() $f_2(x,y,z,u)\in (x,y,z,u)^2$
.
$f_2(x,y,z,u)\in (x,y,z,u)^2$
.
Assume that the assertion is not true. Let
![]() $\pi : \mathcal Y\to \mathcal {X}$
be the morphism defined in Definition 3.0.1, from which we keep the notation. Then the chain of fibres
$\pi : \mathcal Y\to \mathcal {X}$
be the morphism defined in Definition 3.0.1, from which we keep the notation. Then the chain of fibres
![]() $F_p^1\cup \dots \cup F_p^{r-1}$
of
$F_p^1\cup \dots \cup F_p^{r-1}$
of
![]() $\pi ^{-1}(S_0)$
contracted to p by
$\pi ^{-1}(S_0)$
contracted to p by
![]() $\pi $
intersects the singular locus of every divisor
$\pi $
intersects the singular locus of every divisor
![]() $\mathcal S^i$
. In particular, there exists an analytic s-multisection
$\mathcal S^i$
. In particular, there exists an analytic s-multisection
![]() $\gamma $
of
$\gamma $
of
![]() $\mathcal {X}$
(with
$\mathcal {X}$
(with
![]() $s\geqslant r$
) passing through p, whose general point is a singular point of an irreducible component of
$s\geqslant r$
) passing through p, whose general point is a singular point of an irreducible component of
![]() $S\cap \mathcal {X}_t$
, with t general. Every analytic s-multisection of
$S\cap \mathcal {X}_t$
, with t general. Every analytic s-multisection of
![]() $\mathcal {X}\to \mathbb {D}$
at p gives rise to s distinct continuous sections
$\mathcal {X}\to \mathbb {D}$
at p gives rise to s distinct continuous sections
![]() $\gamma ^1,\dots ,\gamma ^s$
over
$\gamma ^1,\dots ,\gamma ^s$
over
![]() $\mathbb {D}^o=\mathbb {D}\setminus \{a+i0\,|\, 0<a<1\}$
, which are holomorphic on
$\mathbb {D}^o=\mathbb {D}\setminus \{a+i0\,|\, 0<a<1\}$
, which are holomorphic on
![]() $\mathbb {D}^o\setminus \underline 0$
. If t varies in
$\mathbb {D}^o\setminus \underline 0$
. If t varies in
![]() $\mathbb {D}^o$
, then there exists a one-parameter analytic family of irreducible surfaces
$\mathbb {D}^o$
, then there exists a one-parameter analytic family of irreducible surfaces
![]() $\mathcal Z\subset S$
, singular along
$\mathcal Z\subset S$
, singular along
![]() $\gamma ^1$
, whose fibre
$\gamma ^1$
, whose fibre
![]() $\mathcal Z_t$
over
$\mathcal Z_t$
over
![]() $t\neq 0$
is an irreducible component of
$t\neq 0$
is an irreducible component of
![]() $S\cap \mathcal {X}_t$
and whose fibre over
$S\cap \mathcal {X}_t$
and whose fibre over
![]() $0$
is
$0$
is
![]() $\mathcal Z_0=S_0$
. The equation of
$\mathcal Z_0=S_0$
. The equation of
![]() $\mathcal Z_t$
in
$\mathcal Z_t$
in
![]() $\mathbb {A}^4$
with coordinates
$\mathbb {A}^4$
with coordinates
![]() $(x,y,z,u)$
is given by
$(x,y,z,u)$
is given by
 $$ \begin{align*} \left\{\begin{array}{l} p(x,y,z,u;t)=0\\ xy=t,\,\, \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{l} p(x,y,z,u;t)=0\\ xy=t,\,\, \end{array}\right. \end{align*} $$
where
![]() $p(x,y,z,u;t)=0$
is an analytic function in
$p(x,y,z,u;t)=0$
is an analytic function in
![]() $(x,y,z,u)$
, whose coefficients are continuous functions in the variable
$(x,y,z,u)$
, whose coefficients are continuous functions in the variable
![]() $t\in \mathbb {D}^o$
which are holomorphic on
$t\in \mathbb {D}^o$
which are holomorphic on
![]() $\mathbb {D}^o\setminus \underline 0$
. If
$\mathbb {D}^o\setminus \underline 0$
. If
then by the hypothesis that the general fibre of
![]() $\mathcal Z$
is singular along
$\mathcal Z$
is singular along
![]() $\gamma $
, we have that
$\gamma $
, we have that
where
![]() $g_2(x-x(t),y-y(t),z-z(t),u-u(t))\in (x-x(t),y-y(t),z-z(t),u-u(t))^2$
.
$g_2(x-x(t),y-y(t),z-z(t),u-u(t))\in (x-x(t),y-y(t),z-z(t),u-u(t))^2$
.
We moreover have that
![]() $p(x,y,z,u;t)$
specializes to
$p(x,y,z,u;t)$
specializes to
![]() $p(x,y,z,u;0)=z+f_2(x,y,z,u)\\ =z-z(0)+f_2(x-x(0),y-y(0),z-z(0),u-u(0))$
as t goes to
$p(x,y,z,u;0)=z+f_2(x,y,z,u)\\ =z-z(0)+f_2(x-x(0),y-y(0),z-z(0),u-u(0))$
as t goes to
![]() $0$
. This is not possible. Thus, every irreducible component of the general fibre of a deformation
$0$
. This is not possible. Thus, every irreducible component of the general fibre of a deformation
![]() $S\subset \mathcal {X}$
of
$S\subset \mathcal {X}$
of
![]() $S_0$
is smooth in a neighborhood of p.
$S_0$
is smooth in a neighborhood of p.
3.2. Deformations of
 $T_1$
singularities
$T_1$
singularities
3.2.1. Deformations not in
 $\mathcal {X}_0$
of surfaces with
$\mathcal {X}_0$
of surfaces with
 $T_1$
singularities
$T_1$
singularities
In this section, we prove that the only singularity of a surface in
![]() $\mathcal {X}_t$
, with
$\mathcal {X}_t$
, with
![]() $t\neq 0$
, to which a
$t\neq 0$
, to which a
![]() $T_1$
singularity of a surface
$T_1$
singularity of a surface
![]() $S_0\subset \mathcal {X}_0$
may be deformed is a node.
$S_0\subset \mathcal {X}_0$
may be deformed is a node.
Lemma 3.2. Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a reduced effective Cartier divisor, with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a reduced effective Cartier divisor, with
![]() $S_A\subset A$
and
$S_A\subset A$
and
![]() $S_B\subset B$
as above. Let p be a point of the intersection curve
$S_B\subset B$
as above. Let p be a point of the intersection curve
![]() $C=S_A\cap S_B\subset R$
, where
$C=S_A\cap S_B\subset R$
, where
![]() $S_0$
has a
$S_0$
has a
![]() $T_1$
singularity. Let
$T_1$
singularity. Let
![]() $ S\subset \mathcal {X}$
be a deformation of
$ S\subset \mathcal {X}$
be a deformation of
![]() $S_0$
not in
$S_0$
not in
![]() $\mathcal {X}_0$
. Then there exists a sufficiently small analytic neighborhood of p in
$\mathcal {X}_0$
. Then there exists a sufficiently small analytic neighborhood of p in
![]() $\mathcal {X}$
such that all irreducible components of the general fibre of
$\mathcal {X}$
such that all irreducible components of the general fibre of
![]() $ S$
in that neighborhood are smooth or are
$ S$
in that neighborhood are smooth or are
![]() $1$
-nodal.
$1$
-nodal.
Proof. By Proposition 3.1, if
![]() $ S\subset \mathcal {X}$
is any deformation of
$ S\subset \mathcal {X}$
is any deformation of
![]() $S_0$
not in
$S_0$
not in
![]() $\mathcal {X}_0$
, then all irreducible components of the general fibre of S have, in a sufficiently small neighborhood of p, only isolated singularities. We want to prove that if the
$\mathcal {X}_0$
, then all irreducible components of the general fibre of S have, in a sufficiently small neighborhood of p, only isolated singularities. We want to prove that if the
![]() $T_1$
singularity of
$T_1$
singularity of
![]() $S_0$
at p is limit of an isolated singularity, then this is a node. We argue as in the proof of Proposition 3.1.
$S_0$
at p is limit of an isolated singularity, then this is a node. We argue as in the proof of Proposition 3.1.
Let
![]() $\mathbb {D}_\epsilon =\mathbb {D}(\underline 0,\epsilon )\subset \mathbb {A}^1$
be the open disc with center at the origin and radius
$\mathbb {D}_\epsilon =\mathbb {D}(\underline 0,\epsilon )\subset \mathbb {A}^1$
be the open disc with center at the origin and radius
![]() $\epsilon $
and let
$\epsilon $
and let
![]() ${\mathbb {D}_\epsilon ^o=\mathbb {D}(\underline 0,\epsilon )\setminus \{a+i0\,|\, 0<a<\epsilon \}}$
. We denote by
${\mathbb {D}_\epsilon ^o=\mathbb {D}(\underline 0,\epsilon )\setminus \{a+i0\,|\, 0<a<\epsilon \}}$
. We denote by
![]() $t=a+ib$
the coordinate on
$t=a+ib$
the coordinate on
![]() $\mathbb {D}_\epsilon $
and by
$\mathbb {D}_\epsilon $
and by
![]() $(x,y,z,u)$
the coordinates in
$(x,y,z,u)$
the coordinates in
![]() $\mathbb {A}^4$
. In
$\mathbb {A}^4$
. In
![]() $\mathbb {A}^4\times \mathbb {D}_\epsilon ^o$
, we consider a one parameter family of
$\mathbb {A}^4\times \mathbb {D}_\epsilon ^o$
, we consider a one parameter family of
![]() $3$
-folds
$3$
-folds
where
![]() $p(x,y,z,u;t)$
is a polynomial in
$p(x,y,z,u;t)$
is a polynomial in
![]() $x,y,z,u$
whose coefficients are holomorphic functions on
$x,y,z,u$
whose coefficients are holomorphic functions on
![]() $\mathbb {D}_\epsilon ^o\setminus \underline 0$
, continuous in
$\mathbb {D}_\epsilon ^o\setminus \underline 0$
, continuous in
![]() $\underline 0$
, and the one parameter family of
$\underline 0$
, and the one parameter family of
![]() $3$
-folds
$3$
-folds
Assume that the surface
 $$ \begin{align} S_0=\mathcal S_0\cap \mathcal{X}_0: \left\{\begin{array}{l} p(x,y,z,u;0)= x+y+p_2(x,y,z,u)+o(3)=0\\ xy=0\,\, \end{array}\right. \end{align} $$
$$ \begin{align} S_0=\mathcal S_0\cap \mathcal{X}_0: \left\{\begin{array}{l} p(x,y,z,u;0)= x+y+p_2(x,y,z,u)+o(3)=0\\ xy=0\,\, \end{array}\right. \end{align} $$
has a
![]() $T_1$
singularity at
$T_1$
singularity at
![]() $\underline 0$
, where
$\underline 0$
, where
![]() $p_2(x,y,z,u)$
is the homogeneous part of degree
$p_2(x,y,z,u)$
is the homogeneous part of degree
![]() $2$
of
$2$
of
![]() $p(x,y,z,u;0)$
, where
$p(x,y,z,u;0)$
, where
![]() $o(3)$
is the sum of terms of degree at least
$o(3)$
is the sum of terms of degree at least
![]() $3$
in
$3$
in
![]() $p(x,y,z,u;0)$
, and where, by assumption,
$p(x,y,z,u;0)$
, and where, by assumption,
![]() $p_2(0,0,z,u)$
has nonzero discriminant.
$p_2(0,0,z,u)$
has nonzero discriminant.
Assume that, for
![]() $t\neq 0$
, there exists
$t\neq 0$
, there exists
![]() $q(t)=(x(t), y(t),z(t),w(t);t)\in S_t=\mathcal S_t\cap \mathcal {X}_t$
specializing to
$q(t)=(x(t), y(t),z(t),w(t);t)\in S_t=\mathcal S_t\cap \mathcal {X}_t$
specializing to
![]() $\underline 0$
, as t goes to
$\underline 0$
, as t goes to
![]() $\underline 0$
and such that
$\underline 0$
and such that
![]() $S_t$
has a singular point at
$S_t$
has a singular point at
![]() $q(t)$
. Thus,
$q(t)$
. Thus,
![]() $\mathcal S_t$
is smooth at
$\mathcal S_t$
is smooth at
![]() $q(t)$
since
$q(t)$
since
![]() $\mathcal S_0$
is smooth at
$\mathcal S_0$
is smooth at
![]() $q(0)=\underline 0$
, and we have that
$q(0)=\underline 0$
, and we have that
In particular, there exists a function
![]() $c(t)$
, which is nonzero if
$c(t)$
, which is nonzero if
![]() $t\neq 0$
, such that
$t\neq 0$
, such that
 $$ \begin{align*} y(t)(x-x(t))+x(t)(y-y(t))& = c(t)\frac{\partial p}{\partial x}|_{q(t)}(x-x(t))+c(t)\frac{\partial p}{\partial y}|_{q(t)}(y-y(t))\\ &\quad + c(t)\frac{\partial p}{\partial z}|_{q(t)}(z-z(t))+c(t)\frac{\partial p}{\partial u}|_{q(t)}(u-u(t)), \end{align*} $$
$$ \begin{align*} y(t)(x-x(t))+x(t)(y-y(t))& = c(t)\frac{\partial p}{\partial x}|_{q(t)}(x-x(t))+c(t)\frac{\partial p}{\partial y}|_{q(t)}(y-y(t))\\ &\quad + c(t)\frac{\partial p}{\partial z}|_{q(t)}(z-z(t))+c(t)\frac{\partial p}{\partial u}|_{q(t)}(u-u(t)), \end{align*} $$
from which we deduce that
As t goes to
![]() $\underline 0$
,
$\underline 0$
,
![]() $c(0)=0$
, since
$c(0)=0$
, since
![]() $x(t)\neq 0\neq y(t)$
if
$x(t)\neq 0\neq y(t)$
if
![]() $t\neq 0$
but
$t\neq 0$
but
![]() $x(0)=y(0)=0$
and
$x(0)=y(0)=0$
and
![]() $\frac {\partial p}{\partial x}|_{q(t)}\neq 0\neq \frac {\partial p}{\partial y}|_{q(t)}$
for any t in a neighborhood of
$\frac {\partial p}{\partial x}|_{q(t)}\neq 0\neq \frac {\partial p}{\partial y}|_{q(t)}$
for any t in a neighborhood of
![]() $\underline 0$
. We now write down the local equations
$\underline 0$
. We now write down the local equations
of
![]() $\mathcal {X}_t$
at
$\mathcal {X}_t$
at
![]() $q(t)$
, and the local equation
$q(t)$
, and the local equation
 $$ \begin{align} \,\,\,\,\,\, \mathcal S_t & : \frac{\partial p}{\partial x}|_{q(t)}(x-x(t))+\frac{\partial p}{\partial y}|_{q(t)}(y-y(t))\\ &+ \frac{\partial p}{\partial x\partial y}|_{q(t)}(x-x(t))(y-y(t))+\frac{\partial p}{\partial x\partial z}|_{q(t)}(x-x(t))(z-z(t))\nonumber \\ &+ \frac{\partial p}{\partial x\partial u}|_{q(t)}(x-x(t))(u-u(t))+\frac{\partial p}{\partial y\partial z}|_{q(t)}(y-y(t))(z-z(t))\nonumber \\ &+ \frac{\partial p}{\partial y\partial u}|_{q(t)}(y-y(t))(u-u(t))+\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\nonumber \\ &+ \frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}(x-x(t))^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}(y-y(t))^2 + \frac{1}{2} \frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2\nonumber \\ &+ \frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2 + o(3)=0\nonumber \end{align} $$
$$ \begin{align} \,\,\,\,\,\, \mathcal S_t & : \frac{\partial p}{\partial x}|_{q(t)}(x-x(t))+\frac{\partial p}{\partial y}|_{q(t)}(y-y(t))\\ &+ \frac{\partial p}{\partial x\partial y}|_{q(t)}(x-x(t))(y-y(t))+\frac{\partial p}{\partial x\partial z}|_{q(t)}(x-x(t))(z-z(t))\nonumber \\ &+ \frac{\partial p}{\partial x\partial u}|_{q(t)}(x-x(t))(u-u(t))+\frac{\partial p}{\partial y\partial z}|_{q(t)}(y-y(t))(z-z(t))\nonumber \\ &+ \frac{\partial p}{\partial y\partial u}|_{q(t)}(y-y(t))(u-u(t))+\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\nonumber \\ &+ \frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}(x-x(t))^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}(y-y(t))^2 + \frac{1}{2} \frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2\nonumber \\ &+ \frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2 + o(3)=0\nonumber \end{align} $$
of
![]() $\mathcal S_t$
at
$\mathcal S_t$
at
![]() $q(t)$
, where
$q(t)$
, where
![]() $o(3)\in (x-x(t), y-y(t), z-z(t), u-u(t))^3$
. By (3.4), one may write
$o(3)\in (x-x(t), y-y(t), z-z(t), u-u(t))^3$
. By (3.4), one may write
Let d be the maximum degree of
![]() $x-x(t)$
in (3.5). By substituting in (3.5), by multiplying by
$x-x(t)$
in (3.5). By substituting in (3.5), by multiplying by
![]() ${y^d= (y-y(t)+y(t))^d}$
, and by using that
${y^d= (y-y(t)+y(t))^d}$
, and by using that
![]() $T_{q(t)}(\mathcal S_t)=T_{q(t)}(\mathcal {X}_t)$
(i.e.,
$T_{q(t)}(\mathcal S_t)=T_{q(t)}(\mathcal {X}_t)$
(i.e.,
![]() $y(t)\frac {\partial p}{\partial y}|_{q(t)}=x(t)\frac {\partial p}{\partial x}|_{q(t)}$
) for any
$y(t)\frac {\partial p}{\partial y}|_{q(t)}=x(t)\frac {\partial p}{\partial x}|_{q(t)}$
) for any
![]() $t\neq 0$
, we find that the local equation of
$t\neq 0$
, we find that the local equation of
![]() $S_t=\mathcal S_t\cap \mathcal {X}_t$
is given by
$S_t=\mathcal S_t\cap \mathcal {X}_t$
is given by
 $$ \begin{align*} S_t & : \frac{\partial p}{\partial x}|_{q(t)}\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber\\[3pt] & + \Big( \frac{\partial p}{\partial x\partial y}|_{q(t)}(y-y(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber\\[3pt] & + \Big(\frac{\partial p}{\partial x\partial z}|_{q(t)}(z-z(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber \\[3pt] & + \Big( \frac{\partial p}{\partial x\partial u}|_{q(t)}(u-u(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1} \\[3pt] &+ \frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}\Big(-x(t)(y-y(t))\Big)^2\Big(y-y(t)+y(t)\Big)^{d-2} \\[3pt] & + \frac{\partial p}{\partial y}|_{q(t)}\Big(y-y(t)\Big)\Big(y-y(t)+y(t)\Big)^{d}\\[3pt]& + \Big(\frac{\partial p}{\partial y\partial z}|_{q(t)}(z-z(t)) + \frac{\partial p}{\partial y\partial u}|_{q(t)}(u-u(t))\Big)\Big(y-y(t)\Big)\Big(y-y(t)+y(t)\Big)^d \\[3pt] & + \Big(\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}(y-y(t))^2+\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\Big)\Big(y-y(t)+y(t)\Big)^{d} \\[3pt] & + \Big(\frac{1}{2} \frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2 + \frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2\Big)\Big(y-y(t)+y(t)\Big)^d + o(3)\\[3pt]& = y(t)^{d-2}\Big(\frac{\partial p}{\partial y}|_{q(t)}y(t)-\frac{\partial p}{\partial x\partial y}|_{q(t)}x(t)y(t) +\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}x(t)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}y(t)^2\Big)\Big(y-y(t)\Big)^2\\[3pt] & + y(t)^{d-1}\Big(y(t)\frac{\partial p}{\partial y\partial z}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big)\Big(y-y(t)\Big)\Big(z-z(t)\Big)\\[3pt] & + y(t)^{d-1}\Big(y(t)\frac{\partial p}{\partial y\partial u}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big)\Big(y-y(t)\Big)\Big(u-u(t)\Big)\\[3pt] & + y(t)^{d} \Big(\frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2+\frac{1}{2}\frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2\Big)\\[3pt] & + y(t)^{d} \Big(\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\Big)+o(3)=0. \end{align*} $$
$$ \begin{align*} S_t & : \frac{\partial p}{\partial x}|_{q(t)}\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber\\[3pt] & + \Big( \frac{\partial p}{\partial x\partial y}|_{q(t)}(y-y(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber\\[3pt] & + \Big(\frac{\partial p}{\partial x\partial z}|_{q(t)}(z-z(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1}\nonumber \\[3pt] & + \Big( \frac{\partial p}{\partial x\partial u}|_{q(t)}(u-u(t))\Big)\Big(-x(t)(y-y(t))\Big)\Big(y-y(t)+y(t)\Big)^{d-1} \\[3pt] &+ \frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}\Big(-x(t)(y-y(t))\Big)^2\Big(y-y(t)+y(t)\Big)^{d-2} \\[3pt] & + \frac{\partial p}{\partial y}|_{q(t)}\Big(y-y(t)\Big)\Big(y-y(t)+y(t)\Big)^{d}\\[3pt]& + \Big(\frac{\partial p}{\partial y\partial z}|_{q(t)}(z-z(t)) + \frac{\partial p}{\partial y\partial u}|_{q(t)}(u-u(t))\Big)\Big(y-y(t)\Big)\Big(y-y(t)+y(t)\Big)^d \\[3pt] & + \Big(\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}(y-y(t))^2+\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\Big)\Big(y-y(t)+y(t)\Big)^{d} \\[3pt] & + \Big(\frac{1}{2} \frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2 + \frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2\Big)\Big(y-y(t)+y(t)\Big)^d + o(3)\\[3pt]& = y(t)^{d-2}\Big(\frac{\partial p}{\partial y}|_{q(t)}y(t)-\frac{\partial p}{\partial x\partial y}|_{q(t)}x(t)y(t) +\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}x(t)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}y(t)^2\Big)\Big(y-y(t)\Big)^2\\[3pt] & + y(t)^{d-1}\Big(y(t)\frac{\partial p}{\partial y\partial z}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big)\Big(y-y(t)\Big)\Big(z-z(t)\Big)\\[3pt] & + y(t)^{d-1}\Big(y(t)\frac{\partial p}{\partial y\partial u}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big)\Big(y-y(t)\Big)\Big(u-u(t)\Big)\\[3pt] & + y(t)^{d} \Big(\frac{1}{2}\frac{\partial p}{\partial z^2}|_{q(t)}(z-z(t))^2+\frac{1}{2}\frac{\partial p}{\partial u^2}|_{q(t)}(u-u(t))^2\Big)\\[3pt] & + y(t)^{d} \Big(\frac{\partial p}{\partial u\partial z}|_{q(t)}(u-u(t))(z-z(t))\Big)+o(3)=0. \end{align*} $$
Up to the irrelevant factor
![]() $y(t)^{d-2}$
, the Hessian matrix at
$y(t)^{d-2}$
, the Hessian matrix at
![]() $q(t)$
of the above polynomial is
$q(t)$
of the above polynomial is
 $$ \begin{align} H_{q(t)}=\left(\begin{array}{ccc}A_{11}(t) & A_{12}(t) & A_{13}(t) \\ A_{12}(t) & \frac{y(t)^2}{2}\frac{\partial p}{\partial z^2}|_{q(t)} & \frac{y(t)^2}{2}\frac{\partial p}{\partial z\partial u}|_{q(t)} \\ A_{13}(t) & \frac{y(t)^2}{2}\frac{\partial p}{\partial z\partial u}|_{q(t)} & \frac{y(t)^2}{2}\frac{\partial p}{\partial u^2}|_{q(t)}\end{array}\right), \end{align} $$
$$ \begin{align} H_{q(t)}=\left(\begin{array}{ccc}A_{11}(t) & A_{12}(t) & A_{13}(t) \\ A_{12}(t) & \frac{y(t)^2}{2}\frac{\partial p}{\partial z^2}|_{q(t)} & \frac{y(t)^2}{2}\frac{\partial p}{\partial z\partial u}|_{q(t)} \\ A_{13}(t) & \frac{y(t)^2}{2}\frac{\partial p}{\partial z\partial u}|_{q(t)} & \frac{y(t)^2}{2}\frac{\partial p}{\partial u^2}|_{q(t)}\end{array}\right), \end{align} $$
where
 $$ \begin{align*} A_{11}(t) & = \frac{\partial p}{\partial y}|_{q(t)}y(t)-\frac{\partial p}{\partial x\partial y}|_{q(t)}x(t)y(t)+\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}x(t)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}y(t)^2,\\[3pt] A_{12}(t) & = \frac{y(t)}{2}\Big(y(t)\frac{\partial p}{\partial y\partial z}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big),\\[3pt] A_{13}(t) & = \frac{y(t)}{2}\Big(y(t)\frac{\partial p}{\partial y\partial u}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big). \end{align*} $$
$$ \begin{align*} A_{11}(t) & = \frac{\partial p}{\partial y}|_{q(t)}y(t)-\frac{\partial p}{\partial x\partial y}|_{q(t)}x(t)y(t)+\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}x(t)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}y(t)^2,\\[3pt] A_{12}(t) & = \frac{y(t)}{2}\Big(y(t)\frac{\partial p}{\partial y\partial z}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big),\\[3pt] A_{13}(t) & = \frac{y(t)}{2}\Big(y(t)\frac{\partial p}{\partial y\partial u}|_{q(t)}-x(t)\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big). \end{align*} $$
Now
![]() $S_t$
has a node at
$S_t$
has a node at
![]() $q(t)$
if and only if
$q(t)$
if and only if
![]() $\det (H_{q(t)})\neq 0$
. If we substitute the equalities (3.2) in
$\det (H_{q(t)})\neq 0$
. If we substitute the equalities (3.2) in
![]() $H_{q(t)}$
, we see that this matrix has the first column divisible by
$H_{q(t)}$
, we see that this matrix has the first column divisible by
![]() $c(t)$
and the second and third columns divisible by
$c(t)$
and the second and third columns divisible by
![]() $c(t)^2$
. Let
$c(t)^2$
. Let
![]() $B_{q(t)}$
be the matrix obtained by
$B_{q(t)}$
be the matrix obtained by
![]() $H_{q(t)}$
by dividing the first column by
$H_{q(t)}$
by dividing the first column by
![]() $c(t)$
and the second and third columns by
$c(t)$
and the second and third columns by
![]() $c(t)^2$
. We have that
$c(t)^2$
. We have that
 $$ \begin{align} B_{q(t)}=\left(\begin{array}{ccc}B_{11}(t) & B_{12}(t) & B_{13}(t) \\ B_{21}(t) & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z^2}|_{q(t)} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z\partial u}|_{q(t)} \\ B_{31}(t) &\frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z\partial u}|_{q(t)} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial u^2}|_{q(t)}\end{array}\right), \end{align} $$
$$ \begin{align} B_{q(t)}=\left(\begin{array}{ccc}B_{11}(t) & B_{12}(t) & B_{13}(t) \\ B_{21}(t) & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z^2}|_{q(t)} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z\partial u}|_{q(t)} \\ B_{31}(t) &\frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial z\partial u}|_{q(t)} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{q(t)})^2\frac{\partial p}{\partial u^2}|_{q(t)}\end{array}\right), \end{align} $$
where
 $$ \begin{align*} B_{11}(t) & = \frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x}|_{q(t)}+ c(t)\Big(-\frac{\partial p}{\partial x\partial y}|_{q(t)}\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y}|_{q(t)}\\[3pt] &\quad+\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}\Big(\frac{\partial p}{\partial y}|_{q(t)}\Big)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}\Big(\frac{\partial p}{\partial x}|_{q(t)}\Big)^2\Big),\\[3pt] B_{21}(t) & = \frac{1}{2}\frac{\partial p}{\partial x}|_{q(t)}c(t)\Big(\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y\partial z}|_{q(t)}-\frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big),\\[3pt] B_{31}(t) & = \frac{1}{2}\frac{\partial p}{\partial x}|_{q(t)}c(t)\Big(\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y\partial u}|_{q(t)}-\frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big). \end{align*} $$
$$ \begin{align*} B_{11}(t) & = \frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x}|_{q(t)}+ c(t)\Big(-\frac{\partial p}{\partial x\partial y}|_{q(t)}\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y}|_{q(t)}\\[3pt] &\quad+\frac{1}{2}\frac{\partial p}{\partial x^2}|_{q(t)}\Big(\frac{\partial p}{\partial y}|_{q(t)}\Big)^2+\frac{1}{2}\frac{\partial p}{\partial y^2}|_{q(t)}\Big(\frac{\partial p}{\partial x}|_{q(t)}\Big)^2\Big),\\[3pt] B_{21}(t) & = \frac{1}{2}\frac{\partial p}{\partial x}|_{q(t)}c(t)\Big(\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y\partial z}|_{q(t)}-\frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x\partial z}|_{q(t)}\Big),\\[3pt] B_{31}(t) & = \frac{1}{2}\frac{\partial p}{\partial x}|_{q(t)}c(t)\Big(\frac{\partial p}{\partial x}|_{q(t)}\frac{\partial p}{\partial y\partial u}|_{q(t)}-\frac{\partial p}{\partial y}|_{q(t)}\frac{\partial p}{\partial x\partial u}|_{q(t)}\Big). \end{align*} $$
As t goes to
![]() $0$
,
$0$
,
![]() $c(t)$
goes to
$c(t)$
goes to
![]() $0$
and the matrix
$0$
and the matrix
![]() $B_{q(t)}$
specializes to the matrix
$B_{q(t)}$
specializes to the matrix
 $$ \begin{align} B_{\underline 0}=\left(\begin{array}{ccc}\frac{\partial p}{\partial y}|_{\underline 0}\frac{\partial p}{\partial x}|_{\underline 0} & B_{12}(0) & B_{13}(0) \\ 0 & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z^2}|_{\underline 0} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z\partial u}|_{\underline 0} \\ 0&\frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z\partial u}|_{\underline 0} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial u^2}|_{\underline 0}\end{array}\right). \end{align} $$
$$ \begin{align} B_{\underline 0}=\left(\begin{array}{ccc}\frac{\partial p}{\partial y}|_{\underline 0}\frac{\partial p}{\partial x}|_{\underline 0} & B_{12}(0) & B_{13}(0) \\ 0 & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z^2}|_{\underline 0} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z\partial u}|_{\underline 0} \\ 0&\frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial z\partial u}|_{\underline 0} & \frac{1}{2}(\frac{\partial p}{\partial x}|_{\underline 0})^2\frac{\partial p}{\partial u^2}|_{\underline 0}\end{array}\right). \end{align} $$
Using that
![]() $\frac {\partial p}{\partial x}|_{\underline 0}=1=\frac {\partial p}{\partial y}|_{\underline 0}$
, we see that
$\frac {\partial p}{\partial x}|_{\underline 0}=1=\frac {\partial p}{\partial y}|_{\underline 0}$
, we see that
![]() $\det (B_{\underline 0})$
coincides with the discriminant of the degree
$\det (B_{\underline 0})$
coincides with the discriminant of the degree
![]() $2$
homogeneous polynomial
$2$
homogeneous polynomial
![]() $p_2(0,0,z,u)$
, which is nonzero by the hypothesis that
$p_2(0,0,z,u)$
, which is nonzero by the hypothesis that
![]() $S_0$
has a
$S_0$
has a
![]() $T_1$
singularity at
$T_1$
singularity at
![]() $\underline 0$
. We finally deduce that
$\underline 0$
. We finally deduce that
![]() $\det (B_{q(t)})\neq 0\neq \det (H_{q(t)})$
and thus the surface
$\det (B_{q(t)})\neq 0\neq \det (H_{q(t)})$
and thus the surface
![]() $S_t$
has a node at
$S_t$
has a node at
![]() $q(t)$
for
$q(t)$
for
![]() $t\neq 0$
.
$t\neq 0$
.
3.2.2. Equisingular deformations of surfaces with
 $T_1$
singularities
$T_1$
singularities
We go on considering the setting we introduced at the beginning of Section 3. Assume that
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
is a surface with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
is a surface with
![]() $S_A$
and
$S_A$
and
![]() $S_B$
smooth, intersecting transversally along
$S_B$
smooth, intersecting transversally along
![]() $R=A\cap B$
, except for
$R=A\cap B$
, except for
![]() $\delta $
distinct points
$\delta $
distinct points
![]() $p_1,\dots p_\delta \in S_A\cap S_B$
, where
$p_1,\dots p_\delta \in S_A\cap S_B$
, where
![]() $S_0$
has a singularity of type
$S_0$
has a singularity of type
![]() $T_1$
. We recall the standard exact sequence
$T_1$
. We recall the standard exact sequence
where
![]() $\Theta _{S_0} = \mathfrak {hom}(\Omega _{S_0}^1,\mathcal {O}_{S_0})$
is the tangent sheaf of
$\Theta _{S_0} = \mathfrak {hom}(\Omega _{S_0}^1,\mathcal {O}_{S_0})$
is the tangent sheaf of
![]() $S_0,$
$S_0,$
![]() $\Theta _{\mathcal {X}}|_{S_0}$
is the tangent sheaf of
$\Theta _{\mathcal {X}}|_{S_0}$
is the tangent sheaf of
![]() $\mathcal {X}$
restricted to
$\mathcal {X}$
restricted to
![]() $S_0$
,
$S_0$
,
![]() $\mathcal N_{S_0|\mathcal {X}}$
is the normal bundle of
$\mathcal N_{S_0|\mathcal {X}}$
is the normal bundle of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
, and
$\mathcal {X}$
, and
![]() $T^1_{S_0}$
is the first cotangent sheaf of
$T^1_{S_0}$
is the first cotangent sheaf of
![]() $S_0$
[Reference Sernesi20, Section 1.1.3]. The latter is supported on the singular locus
$S_0$
[Reference Sernesi20, Section 1.1.3]. The latter is supported on the singular locus
![]() $\operatorname {Sing}(S_0)=S_A\cap S_B$
. The kernel
$\operatorname {Sing}(S_0)=S_A\cap S_B$
. The kernel
![]() $\mathcal N_{S_0|\mathcal {X}}^\prime $
of
$\mathcal N_{S_0|\mathcal {X}}^\prime $
of
![]() $\beta $
is the so-called equisingular normal sheaf to
$\beta $
is the so-called equisingular normal sheaf to
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
, whose global sections are the first-order locally trivial deformations of
$\mathcal {X}$
, whose global sections are the first-order locally trivial deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
In the sequel, an equisingular (first-order) deformation of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
will be a (first-order) locally trivial deformation of
$\mathcal {X}$
will be a (first-order) locally trivial deformation of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
We will denote by
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}\subset \mathcal H^{\mathcal {X}|\mathbb {D}}$
the locally closed set of equisingular deformations of
$\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}\subset \mathcal H^{\mathcal {X}|\mathbb {D}}$
the locally closed set of equisingular deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
. Similarly, if
$\mathcal {X}_0$
. Similarly, if
![]() $p\in S_0$
is a point, we will denote by
$p\in S_0$
is a point, we will denote by
![]() $\mathcal {ES}_{[S_0], p}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}\subset \mathcal H^{\mathcal {X}|\mathbb {D}}$
the locally closed set of deformations of
$\mathcal {ES}_{[S_0], p}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}\subset \mathcal H^{\mathcal {X}|\mathbb {D}}$
the locally closed set of deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
, which are equisingular at p.
$\mathcal {X}_0$
, which are equisingular at p.
Lemma 3.3. If
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}|\mathbb {D}}\subseteq \mathcal H^{\mathcal {X}|\mathbb {D}}$
is the locally closed set of equisingular deformations of
$\mathcal {ES}_{[S_0]}^{\mathcal {X}|\mathbb {D}}\subseteq \mathcal H^{\mathcal {X}|\mathbb {D}}$
is the locally closed set of equisingular deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
, then
$\mathcal {X}$
, then
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
coincides set-theoretically with
$\mathcal {ES}_{[S_0]}^{\mathcal {X}|\mathbb {D}}$
coincides set-theoretically with
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}$
.
$\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}\subseteq \mathcal H^{\mathcal {X}_0}$
.
Proof. This is a straightforward consequence of Lemma 3.2.
If
![]() $\mathbb {T}_\delta \subset \mathcal H^{\mathcal {X}_0}$
is the Zariski closure of the family of surfaces in
$\mathbb {T}_\delta \subset \mathcal H^{\mathcal {X}_0}$
is the Zariski closure of the family of surfaces in
![]() $\mathcal {X}_0$
with
$\mathcal {X}_0$
with
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
, then every irreducible component of
$T_1$
, then every irreducible component of
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}$
is a Zariski open set in an irreducible component of
$\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}$
is a Zariski open set in an irreducible component of
![]() $\mathbb {T}_\delta $
.
$\mathbb {T}_\delta $
.
Consider the rational map
where
![]() $\mathcal H^R$
is the Hilbert scheme of R, and
$\mathcal H^R$
is the Hilbert scheme of R, and
![]() $\varphi $
maps the general subscheme of
$\varphi $
maps the general subscheme of
![]() $\mathcal {X}_0$
to its intersection with R.
$\mathcal {X}_0$
to its intersection with R.
Lemma 3.4. Let
![]() $[S_0]\in \mathbb {T}_\delta $
be a point corresponding to a surface
$[S_0]\in \mathbb {T}_\delta $
be a point corresponding to a surface
![]() $S_0=S_A\cup S_B$
as above and suppose that
$S_0=S_A\cup S_B$
as above and suppose that
![]() $[S_0]$
is a smooth point of the Hilbert scheme
$[S_0]$
is a smooth point of the Hilbert scheme
![]() $\mathcal H^{\mathcal {X}_0}$
so that there is a unique component
$\mathcal H^{\mathcal {X}_0}$
so that there is a unique component
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
of
$\mathcal H^{\mathcal {X}_0}_{S_0}$
of
![]() $\mathcal H^{\mathcal {X}_0}$
containing
$\mathcal H^{\mathcal {X}_0}$
containing
![]() $S_0$
. Let C be the curve cut out by
$S_0$
. Let C be the curve cut out by
![]() $S_0$
on R. Assume that
$S_0$
on R. Assume that
![]() $h^1(\mathcal N_{C|R}\otimes \mathcal I_{\{p_1,\ldots , p_\delta \}|R})=0$
, where
$h^1(\mathcal N_{C|R}\otimes \mathcal I_{\{p_1,\ldots , p_\delta \}|R})=0$
, where
![]() $p_1,\ldots , p_\delta $
are the nodes of C, which implies that
$p_1,\ldots , p_\delta $
are the nodes of C, which implies that
![]() $\mathcal H^R$
is smooth at the point
$\mathcal H^R$
is smooth at the point
![]() $[C]$
and that the Severi variety of curves on R with
$[C]$
and that the Severi variety of curves on R with
![]() $\delta $
nodes is smooth at the point
$\delta $
nodes is smooth at the point
![]() $[C]$
of codimension
$[C]$
of codimension
![]() $\delta $
in the unique irreducible component
$\delta $
in the unique irreducible component
![]() $\mathcal H^R_C$
of the Hilbert scheme
$\mathcal H^R_C$
of the Hilbert scheme
![]() $\mathcal H^R$
containing
$\mathcal H^R$
containing
![]() $[C]$
. Suppose moreover that the map
$[C]$
. Suppose moreover that the map
is dominant.
Then there is an irreducible component
![]() $\mathbb {T}$
of
$\mathbb {T}$
of
![]() $\mathbb {T}_\delta $
containing
$\mathbb {T}_\delta $
containing
![]() $S_0$
that has codimension at most
$S_0$
that has codimension at most
![]() $\delta $
in
$\delta $
in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
.
$\mathcal H_{S_0}^{\mathcal {X}_0}$
.
Proof. Let
![]() $V\subset \mathcal H_C^R$
be the unique irreducible component of the locally closed set of curves on R with
$V\subset \mathcal H_C^R$
be the unique irreducible component of the locally closed set of curves on R with
![]() $\delta $
nodes that contains the point
$\delta $
nodes that contains the point
![]() $[C]$
. Since
$[C]$
. Since
![]() $[C]$
sits in the image of
$[C]$
sits in the image of
![]() $ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
, V intersects the image of
$ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
, V intersects the image of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
. Since
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
. Since
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
is dominant, the intersection of V with the image of
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
is dominant, the intersection of V with the image of
![]() $ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
is an open dense subset of V; hence, there is an irreducible component
$ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
is an open dense subset of V; hence, there is an irreducible component
![]() $\mathbb {T}$
of
$\mathbb {T}$
of
![]() $\mathbb {T}_\delta $
containing
$\mathbb {T}_\delta $
containing
![]() $S_0$
such that the map
$S_0$
such that the map
is dominant. Let a be the dimension of the general fibre of
![]() $\varphi _{|\mathbb {T}}$
and let b be the dimension of the general fibre of
$\varphi _{|\mathbb {T}}$
and let b be the dimension of the general fibre of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
. Of course,
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
. Of course,
![]() $a\geqslant b$
. We have
$a\geqslant b$
. We have
Hence,
and the assertion follows.
Remark 3.5. Note that in the previous lemma, one has that
![]() $\mathbb {T}$
has exactly codimension
$\mathbb {T}$
has exactly codimension
![]() $\delta $
in
$\delta $
in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
if and only if
$\mathcal H_{S_0}^{\mathcal {X}_0}$
if and only if
![]() $a=b$
.
$a=b$
.
Lemma 3.6. Assume that
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
is a surface with
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
is a surface with
![]() $S_A$
and
$S_A$
and
![]() $S_B$
smooth, intersecting transversally along
$S_B$
smooth, intersecting transversally along
![]() $R=A\cap B$
, except for
$R=A\cap B$
, except for
![]() $\delta $
points
$\delta $
points
![]() $p_1,\dots , p_\delta \in S_A\cap S_B$
, where
$p_1,\dots , p_\delta \in S_A\cap S_B$
, where
![]() $S_0$
has a singularity of type
$S_0$
has a singularity of type
![]() $T_1$
. Then the equisingular first-order infinitesimal deformations of
$T_1$
. Then the equisingular first-order infinitesimal deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
coincide with the equisingular first-order infinitesimal deformations of
$\mathcal {X}$
coincide with the equisingular first-order infinitesimal deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
. More precisely, we have that
$\mathcal {X}_0$
. More precisely, we have that
where
![]() $I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}$
is the ideal sheaf of
$I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}$
is the ideal sheaf of
![]() $\{p_1,\dots ,p_\delta \}$
in
$\{p_1,\dots ,p_\delta \}$
in
![]() $\mathcal {X}_0$
.
$\mathcal {X}_0$
.
Proof. Let
![]() $p=p_i$
, for
$p=p_i$
, for
![]() $i=1,...,\delta $
, be a point where
$i=1,...,\delta $
, be a point where
![]() $S_0$
has a
$S_0$
has a
![]() $T_1$
singularity. Consider the localized exact sequence
$T_1$
singularity. Consider the localized exact sequence
Let
![]() $(x,y,z,u,t)$
be an analytic coordinate system of
$(x,y,z,u,t)$
be an analytic coordinate system of
![]() $\mathcal {X}$
centered at p such that
$\mathcal {X}$
centered at p such that
![]() $\mathcal {X}$
is given by
$\mathcal {X}$
is given by
![]() $xy=t$
and such that we have the following identifications:
$xy=t$
and such that we have the following identifications:
-
• the local ring
 $\mathcal {O}_{{S_0},\,p}=\mathcal {O}_{\mathcal {X},p}/\mathcal I_{{S_0}|\mathcal {X},p}$
of
$\mathcal {O}_{{S_0},\,p}=\mathcal {O}_{\mathcal {X},p}/\mathcal I_{{S_0}|\mathcal {X},p}$
of
 $S_0$
at p is identified with
$S_0$
at p is identified with
 $\mathbb {C}[x,y,z,u]/(h_1,h_2)$
, localized at the origin, where
$\mathbb {C}[x,y,z,u]/(h_1,h_2)$
, localized at the origin, where
 $h_1(x,y,z,u)= x+y+h_{12}(x,y,z,u)$
,
$h_1(x,y,z,u)= x+y+h_{12}(x,y,z,u)$
,
 $h_{12}(x,y,z,u)\in (x,y,z,u)^2$
and
$h_{12}(x,y,z,u)\in (x,y,z,u)^2$
and
 $h_{12}(0,0,z,u)=0$
having a node at
$h_{12}(0,0,z,u)=0$
having a node at
 $\underline 0=p$
, and
$\underline 0=p$
, and
 $h_2(x,y,z,u)=xy$
;
$h_2(x,y,z,u)=xy$
; -
• the
 $\mathcal {O}_{{S_0},p}$
-module
$\mathcal {O}_{{S_0},p}$
-module
 $\mathcal N_{{S_0}|\mathcal {X},\,p}$
is identified with the free
$\mathcal N_{{S_0}|\mathcal {X},\,p}$
is identified with the free
 $\mathcal {O}_{\mathcal {X},\,p}$
-module
$\mathcal {O}_{\mathcal {X},\,p}$
-module
 $\mathfrak {hom}_{\mathcal {O}_{\mathcal {X},\,p}}(\mathcal I_{{S_0}|\mathcal {X} ,\,p}, \mathcal {O}_{S_0,p}),$
generated by the morphisms
$\mathfrak {hom}_{\mathcal {O}_{\mathcal {X},\,p}}(\mathcal I_{{S_0}|\mathcal {X} ,\,p}, \mathcal {O}_{S_0,p}),$
generated by the morphisms
 $h_1^{*}$
and
$h_1^{*}$
and
 $h_2^{*}$
, defined by
$h_2^{*}$
, defined by  $$ \begin{align*}h_i^{*}(s_1(x,y,z,u)h_1(x,y,z,u)+s_2(x,y,z,u)h_2(x,y,z,u))=s_i(x,y,z,u),\,\mbox{for}\, i=1,\,2\end{align*} $$
$$ \begin{align*}h_i^{*}(s_1(x,y,z,u)h_1(x,y,z,u)+s_2(x,y,z,u)h_2(x,y,z,u))=s_i(x,y,z,u),\,\mbox{for}\, i=1,\,2\end{align*} $$
and, finally,
-
• the
 $\mathcal {O}_{S_0,p}$
-module is identified with the free
$\mathcal {O}_{S_0,p}$
-module is identified with the free $$ \begin{align*} (\Theta_{\mathcal{X}}|_{S_0})_{\, p}&\simeq \Theta_{\mathcal{X},p}\otimes \mathcal{O}_{S_0,p}\\ & \simeq \langle \partial /{\partial x},\partial /{\partial y},\partial / {\partial z},\partial / {\partial u},\partial /{\partial t} \rangle _{\mathcal{O}_{S_0,\,p}}/ \langle {\partial}/{\partial t}-x\partial /{\partial y}-y\partial /{\partial x}\rangle \end{align*} $$
$$ \begin{align*} (\Theta_{\mathcal{X}}|_{S_0})_{\, p}&\simeq \Theta_{\mathcal{X},p}\otimes \mathcal{O}_{S_0,p}\\ & \simeq \langle \partial /{\partial x},\partial /{\partial y},\partial / {\partial z},\partial / {\partial u},\partial /{\partial t} \rangle _{\mathcal{O}_{S_0,\,p}}/ \langle {\partial}/{\partial t}-x\partial /{\partial y}-y\partial /{\partial x}\rangle \end{align*} $$
 $\mathcal {O}_{\mathcal {X},\,p}$
-module generated by the derivatives
$\mathcal {O}_{\mathcal {X},\,p}$
-module generated by the derivatives
 $\partial /{\partial x},\partial / {\partial y},\partial /{\partial z}, \partial / {\partial u}.$
$\partial /{\partial x},\partial / {\partial y},\partial /{\partial z}, \partial / {\partial u}.$
With these identifications, the localization
![]() $\alpha _p:(\Theta _{\mathcal {X}}|_{S_0})_{\, p}\rightarrow \mathcal N_{S_0|\mathcal {X},\,p}$
of the sheaf map
$\alpha _p:(\Theta _{\mathcal {X}}|_{S_0})_{\, p}\rightarrow \mathcal N_{S_0|\mathcal {X},\,p}$
of the sheaf map
![]() $\alpha $
from (3.10) is defined by
$\alpha $
from (3.10) is defined by
 $$ \begin{align*} \alpha_p(\partial /{\partial x})&=\Big(s=s_1h_1+s_2h_2\rightarrowtail \partial s/\partial x=_{\mathcal{O}_{S_0,p}} s_1\partial h_1 /{\partial x} +s_2\partial h_2 /{\partial x}\Big)\\ &= (1+\partial h_{12}/\partial x ) h_1^{*}+yh_2^{*},\\ \alpha_p(\partial /{\partial y})&= (1+\partial h_{12}/\partial y ) h^{*}_1+xh^{*}_2,\\ \alpha_p(\partial /{\partial z})&= (\partial h_{12}/\partial z) h^{*}_1 \,\,\,\textrm{and}\\ \alpha_p(\partial /{\partial u})&=(\partial h_{12}/\partial u) h^{*}_1. \end{align*} $$
$$ \begin{align*} \alpha_p(\partial /{\partial x})&=\Big(s=s_1h_1+s_2h_2\rightarrowtail \partial s/\partial x=_{\mathcal{O}_{S_0,p}} s_1\partial h_1 /{\partial x} +s_2\partial h_2 /{\partial x}\Big)\\ &= (1+\partial h_{12}/\partial x ) h_1^{*}+yh_2^{*},\\ \alpha_p(\partial /{\partial y})&= (1+\partial h_{12}/\partial y ) h^{*}_1+xh^{*}_2,\\ \alpha_p(\partial /{\partial z})&= (\partial h_{12}/\partial z) h^{*}_1 \,\,\,\textrm{and}\\ \alpha_p(\partial /{\partial u})&=(\partial h_{12}/\partial u) h^{*}_1. \end{align*} $$
By definition of
![]() $\mathcal N^\prime _{S_0|\mathcal {X}}$
, a local section s of
$\mathcal N^\prime _{S_0|\mathcal {X}}$
, a local section s of
![]() $\mathcal N^\prime _{S_0|\mathcal {X},\,p}$
is such that there exists a local section v of
$\mathcal N^\prime _{S_0|\mathcal {X},\,p}$
is such that there exists a local section v of
![]() ${\Theta _{\mathcal {X}}|_{S_0}}_{\, p}$
with
${\Theta _{\mathcal {X}}|_{S_0}}_{\, p}$
with
such that
![]() $s=\alpha _p(v)$
. Hence, locally at p, first-order equisingular deformations of
$s=\alpha _p(v)$
. Hence, locally at p, first-order equisingular deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
have equations
$\mathcal {X}$
have equations
 $$ \begin{align} \left\{\begin{array}{lll} x+y+h_{12}(x,y,z,u)& + & \epsilon \Big(v_x(1+\partial h_{12}/\partial x)+v_y(1+\partial h_{12}/\partial y)\\ & + &\,\,\,\,\, v_z(\partial h_{12}/\partial z)+v_u(\partial h_{12}/\partial u)\Big)=0\\ xy+\epsilon (yv_x+xv_y) & = & 0. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{lll} x+y+h_{12}(x,y,z,u)& + & \epsilon \Big(v_x(1+\partial h_{12}/\partial x)+v_y(1+\partial h_{12}/\partial y)\\ & + &\,\,\,\,\, v_z(\partial h_{12}/\partial z)+v_u(\partial h_{12}/\partial u)\Big)=0\\ xy+\epsilon (yv_x+xv_y) & = & 0. \end{array}\right. \end{align} $$
The first equation above gives a first-order infinitesimal deformation of the Cartier divisor cutting
![]() $S_0$
on
$S_0$
on
![]() $\mathcal {X}_0$
, while the second equation gives a first-order infinitesimal deformation of
$\mathcal {X}_0$
, while the second equation gives a first-order infinitesimal deformation of
![]() $\mathcal {X}_0$
in
$\mathcal {X}_0$
in
![]() $\mathcal {X}.$
More precisely, by the exact sequence
$\mathcal {X}.$
More precisely, by the exact sequence
one sees that
![]() $xy+\epsilon (yv_x+xv_y)=0$
is the local equation at p of a first-order equisingular deformation of
$xy+\epsilon (yv_x+xv_y)=0$
is the local equation at p of a first-order equisingular deformation of
![]() $\mathcal {X}_0$
in
$\mathcal {X}_0$
in
![]() $\mathcal {X}$
. But
$\mathcal {X}$
. But
![]() $H^0(\mathcal {X}_0, \mathcal N^{\prime }_{\mathcal {X}_0|\mathcal {X}})=H^0(\mathcal {X}_0, \mathcal I_{R|\mathcal {X}_0})=0.$
It follows that the polynomial
$H^0(\mathcal {X}_0, \mathcal N^{\prime }_{\mathcal {X}_0|\mathcal {X}})=H^0(\mathcal {X}_0, \mathcal I_{R|\mathcal {X}_0})=0.$
It follows that the polynomial
![]() $yv_x(x,y,z,u)+xv_y(x,y,z,u)$
in the second equation of (3.14) must be identically zero, proving the first assertion of the lemma. In particular, by expanding
$yv_x(x,y,z,u)+xv_y(x,y,z,u)$
in the second equation of (3.14) must be identically zero, proving the first assertion of the lemma. In particular, by expanding
![]() $v_x$
and
$v_x$
and
![]() $v_y$
in Taylor series, we see that
$v_y$
in Taylor series, we see that
Looking at the first equation of (3.14), we have that
![]() $\frac {\partial h_{12}}{\partial z}(\underline 0)=\frac {\partial h_{12}}{\partial u}(\underline 0)=0$
since
$\frac {\partial h_{12}}{\partial z}(\underline 0)=\frac {\partial h_{12}}{\partial u}(\underline 0)=0$
since
![]() $h_{12}(x,y,z,u)\in (x,y,z,u)^2$
. This shows the inclusion (3.12).
$h_{12}(x,y,z,u)\in (x,y,z,u)^2$
. This shows the inclusion (3.12).
Remark 3.7. The argument in the proof of Lemma 3.6 proves more than stated. In fact, it proves that if
![]() $S_0$
is any surface in
$S_0$
is any surface in
![]() $\mathcal {X}_0$
with
$\mathcal {X}_0$
with
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
at
$T_1$
at
![]() $p_1,\ldots , p_\delta $
(and may be other singularities which we do not care about), the first-order infinitesimal deformations of
$p_1,\ldots , p_\delta $
(and may be other singularities which we do not care about), the first-order infinitesimal deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
which are equisingular at
$\mathcal {X}$
which are equisingular at
![]() $p_1,\ldots , p_\delta $
are a linear subspace of
$p_1,\ldots , p_\delta $
are a linear subspace of
![]() $H^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})$
.
$H^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})$
.
Corollary 3.7.1. Same hypotheses as in Lemma 3.4. Assume moreover that
or, equivalently, that
(assuring that the Hilbert scheme
![]() $\mathcal H^{\mathcal {X}_0}$
is smooth at
$\mathcal H^{\mathcal {X}_0}$
is smooth at
![]() $[S_0]$
). Then the schemes
$[S_0]$
). Then the schemes
![]() $\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}$
and
$\mathcal {ES}_{[S_0]}^{\mathcal {X}_0}$
and
![]() $\mathbb {T}_\delta $
are smooth at
$\mathbb {T}_\delta $
are smooth at
![]() $[S_0]$
of dimension
$[S_0]$
of dimension
![]() $h^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}) )$
, with tangent space
$h^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}) )$
, with tangent space
![]() $T_{[S_0]}(\mathcal {ES}_{[S_0]}^{\mathcal {X}_0})\simeq T_{[S_0]}(\mathbb {T}_\delta )\simeq H^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}) )\simeq H^0(S_0, \mathcal N^{\prime }_{S_0|\mathcal {X}}). $
$T_{[S_0]}(\mathcal {ES}_{[S_0]}^{\mathcal {X}_0})\simeq T_{[S_0]}(\mathbb {T}_\delta )\simeq H^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0}) )\simeq H^0(S_0, \mathcal N^{\prime }_{S_0|\mathcal {X}}). $
Proof. Consider the exact sequence
from which one deduces that
![]() $h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=0$
if and only if
$h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=0$
if and only if
![]() $h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0})=0$
and
$h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0})=0$
and
Assume that
![]() $h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=0$
. Thus,
$h^1(S_0, \mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=0$
. Thus,
![]() $[S_0]$
is a smooth point of
$[S_0]$
is a smooth point of
![]() $\mathcal H^{\mathcal {X}_0}$
. In particular, there exists a unique component
$\mathcal H^{\mathcal {X}_0}$
. In particular, there exists a unique component
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
of
$\mathcal H_{S_0}^{\mathcal {X}_0}$
of
![]() $\mathcal H^{\mathcal {X}_0}$
containing
$\mathcal H^{\mathcal {X}_0}$
containing
![]() $[S_0]$
and having dimension
$[S_0]$
and having dimension
![]() $h^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0})$
at
$h^0(S_0, \mathcal N_{ S_0|\mathcal {X}_0})$
at
![]() $[S_0]$
. Now, by Lemma 3.4, one has that
$[S_0]$
. Now, by Lemma 3.4, one has that
However, by (3.12), one has that
The corollary follows.
We note the following:
Lemma 3.8. Let
![]() $[S_0]\in \mathcal H^{\mathcal {X}|\mathbb {D}}$
be any point corresponding to a reduced effective Cartier divisor
$[S_0]\in \mathcal H^{\mathcal {X}|\mathbb {D}}$
be any point corresponding to a reduced effective Cartier divisor
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
. Assume that
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
. Assume that
![]() $H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then the space of first-order infinitesimal deformations of
$H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then the space of first-order infinitesimal deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}$
is given by
$\mathcal {X}$
is given by
and
is an obstruction space for
![]() $\mathcal {O}_{\mathcal H^{\mathcal {X}|\mathbb {D}}, [S_0]}.$
$\mathcal {O}_{\mathcal H^{\mathcal {X}|\mathbb {D}}, [S_0]}.$
Proof. By the hypothesis, we have
![]() $\mathrm {Ext}^1(\mathcal {O}_{S_0},\mathcal N_{{S_0}|\mathcal {X}_0})\simeq H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
, and by the exact sequence
$\mathrm {Ext}^1(\mathcal {O}_{S_0},\mathcal N_{{S_0}|\mathcal {X}_0})\simeq H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
, and by the exact sequence
we have that
The statement then follows by standard deformation theory.
Corollary 3.8.1. Let
![]() $[S_0]\in \mathcal H^{\mathcal {X}|\mathbb {D}}$
be a point corresponding to a reduced effective Cartier divisor
$[S_0]\in \mathcal H^{\mathcal {X}|\mathbb {D}}$
be a point corresponding to a reduced effective Cartier divisor
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
. Assume that
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
. Assume that
![]() $[S_0]$
belongs to an irreducible component
$[S_0]$
belongs to an irreducible component
![]() $\mathcal H$
of
$\mathcal H$
of
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
![]() $\mathbb {D}$
. Suppose that
$\mathbb {D}$
. Suppose that
![]() $H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then
$H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then
![]() $[S_0]$
is a smooth point for
$[S_0]$
is a smooth point for
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
and
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
and
![]() $\dim (\mathcal H)=\dim (\mathcal H^{\mathcal {X}_0}_{[S_0]})+1$
.
$\dim (\mathcal H)=\dim (\mathcal H^{\mathcal {X}_0}_{[S_0]})+1$
.
Proof. One has
![]() $\dim (\mathcal H)\geqslant \dim (\mathcal H^{\mathcal {X}_0}_{[S_0]})+1=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})+1$
. However,
$\dim (\mathcal H)\geqslant \dim (\mathcal H^{\mathcal {X}_0}_{[S_0]})+1=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})+1$
. However,
![]() $\dim (\mathcal H)\leqslant h^0(S_0,\mathcal N_{S_0|\mathcal {X}})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})+1$
by Lemma 3.8. The assertion follows.
$\dim (\mathcal H)\leqslant h^0(S_0,\mathcal N_{S_0|\mathcal {X}})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})+1$
by Lemma 3.8. The assertion follows.
Corollary 3.8.2. In the same setting as in Lemma 3.6 and same hypotheses as in Lemma 3.4, suppose that (3.15) (or equivalently (3.16)) holds, assuring that
![]() $\mathbb {T}_\delta $
is smooth at
$\mathbb {T}_\delta $
is smooth at
![]() $[S_0]$
of dimension
$[S_0]$
of dimension
![]() $h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta $
. Then for every positive integer
$h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\{p_1,\dots ,p_\delta \}|\mathcal {X}_0})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta $
. Then for every positive integer
![]() $r<\delta $
, the variety
$r<\delta $
, the variety
![]() $\mathbb {T}_r$
is nonempty and
$\mathbb {T}_r$
is nonempty and
![]() $[S_0]\in \mathbb {T}_r$
. More precisely, in an analytic neighborhood of
$[S_0]\in \mathbb {T}_r$
. More precisely, in an analytic neighborhood of
![]() $[S_0]$
,
$[S_0]$
,
![]() $\mathbb {T}_r$
consists of
$\mathbb {T}_r$
consists of
![]() $\delta \choose r$
smooth analytic branches each of dimension
$\delta \choose r$
smooth analytic branches each of dimension
![]() $h^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0})-r$
that intersect at
$h^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0})-r$
that intersect at
![]() $[S_0]$
along a smooth analytic branch of
$[S_0]$
along a smooth analytic branch of
![]() $\mathbb {T}_\delta $
.
$\mathbb {T}_\delta $
.
Informally speaking, this is saying that the
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
of
$T_1$
of
![]() $S_0$
can be independently smoothed inside
$S_0$
can be independently smoothed inside
![]() $\mathcal {X}_0$
.
$\mathcal {X}_0$
.
Proof. We first prove the assertion for
![]() $r=1$
. Let
$r=1$
. Let
![]() $\mathbb {T}$
be the closure of the subset of the Hilbert scheme
$\mathbb {T}$
be the closure of the subset of the Hilbert scheme
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
consisting of all surfaces
$\mathcal H_{S_0}^{\mathcal {X}_0}$
consisting of all surfaces
![]() $S_0^{\prime }$
such that the intersection curve of
$S_0^{\prime }$
such that the intersection curve of
![]() $S_0^{\prime }$
with
$S_0^{\prime }$
with
![]() $R=A\cap B$
is singular with at most nodes. Observe that
$R=A\cap B$
is singular with at most nodes. Observe that
![]() $[S_0]\in \mathbb {T}$
.
$[S_0]\in \mathbb {T}$
.
We claim that any irreducible component of
![]() $\mathbb {T}$
that contains
$\mathbb {T}$
that contains
![]() $[S_0]$
has exactly codimension 1 in
$[S_0]$
has exactly codimension 1 in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
. Indeed, let
$\mathcal H_{S_0}^{\mathcal {X}_0}$
. Indeed, let
![]() $\mathbb {T}'$
be such a component. Consider the dominant map
$\mathbb {T}'$
be such a component. Consider the dominant map
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
as in (3.11), which is defined at a general point of
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
as in (3.11), which is defined at a general point of
![]() $\mathbb {T}'$
.
$\mathbb {T}'$
.
By our hypotheses, the general element in
![]() $\mathcal H_C^R$
is a smooth curve; hence,
$\mathcal H_C^R$
is a smooth curve; hence,
![]() $\mathbb {T}'$
has codimension at least 1 in
$\mathbb {T}'$
has codimension at least 1 in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
. Let
$\mathcal H_{S_0}^{\mathcal {X}_0}$
. Let
![]() $\mathcal T$
be the image of the restriction of
$\mathcal T$
be the image of the restriction of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
to
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
to
![]() $\mathbb {T}'$
. Then
$\mathbb {T}'$
. Then
![]() $\mathcal T$
has codimension 1 in
$\mathcal T$
has codimension 1 in
![]() $\mathcal H_C^R$
.
$\mathcal H_C^R$
.
Let
![]() $\alpha $
be the dimension of the general fibre of
$\alpha $
be the dimension of the general fibre of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
and let
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
and let
![]() $\beta $
be the dimension of the general fibre of the restriction of
$\beta $
be the dimension of the general fibre of the restriction of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
to
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}$
to
![]() $\mathbb {T}'$
. One has
$\mathbb {T}'$
. One has
![]() $\alpha \leqslant \beta $
. Then
$\alpha \leqslant \beta $
. Then
and
Since
![]() $\dim (\mathbb {T}')<\dim (\mathcal H_{S_0}^{\mathcal {X}_0})$
, we have
$\dim (\mathbb {T}')<\dim (\mathcal H_{S_0}^{\mathcal {X}_0})$
, we have
![]() $\dim (\mathbb {T}')=\dim (\mathcal H_{S_0}^{\mathcal {X}_0})-1$
and
$\dim (\mathbb {T}')=\dim (\mathcal H_{S_0}^{\mathcal {X}_0})-1$
and
![]() $\alpha =\beta $
, as claimed.
$\alpha =\beta $
, as claimed.
Now, we consider a suitably small analytic open neighborhood U of
![]() $[S_0]$
in
$[S_0]$
in
![]() $\mathbb {T}$
. Every surface
$\mathbb {T}$
. Every surface
![]() $S_0^{\prime }$
such that
$S_0^{\prime }$
such that
![]() $[S_0^{\prime }]\in U$
has at most
$[S_0^{\prime }]\in U$
has at most
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
.
$T_1$
.
Consider the variety
![]() $I\subset U\times R$
consisting of all pairs
$I\subset U\times R$
consisting of all pairs
![]() $([S_0^{\prime }],q)$
with q a
$([S_0^{\prime }],q)$
with q a
![]() $T_1$
singularity of
$T_1$
singularity of
![]() $S_0^{\prime }$
. Let
$S_0^{\prime }$
. Let
![]() $\pi _1: I\to U$
and
$\pi _1: I\to U$
and
![]() $\pi _2: I\to R$
be the two projections. The former one has finite fibres, implying that every irreducible component of I has dimension
$\pi _2: I\to R$
be the two projections. The former one has finite fibres, implying that every irreducible component of I has dimension
![]() $\dim (\mathcal H_{S_0}^{\mathcal {X}_0})-1$
. As for the latter, it is dominant because we assume the hypotheses of Lemma 3.4. Moreover, if
$\dim (\mathcal H_{S_0}^{\mathcal {X}_0})-1$
. As for the latter, it is dominant because we assume the hypotheses of Lemma 3.4. Moreover, if
![]() $q\in R$
is a point, the fibre
$q\in R$
is a point, the fibre
![]() $\pi _2^{-1}(q)$
is the locally closed set of surfaces
$\pi _2^{-1}(q)$
is the locally closed set of surfaces
![]() $S_0^{\prime }$
in
$S_0^{\prime }$
in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
having a
$\mathcal H_{S_0}^{\mathcal {X}_0}$
having a
![]() $T_1$
singularity in q.
$T_1$
singularity in q.
Let
![]() $V_i$
be a sufficiently small analytic neighborhood of
$V_i$
be a sufficiently small analytic neighborhood of
![]() $p_i$
in R for
$p_i$
in R for
![]() $i=1,\ldots , \delta $
. By the above considerations,
$i=1,\ldots , \delta $
. By the above considerations,
![]() $\pi _1(\pi _2^{-1}(V_i))\subseteq U$
is an analytic open set that parametrizes deformations of
$\pi _1(\pi _2^{-1}(V_i))\subseteq U$
is an analytic open set that parametrizes deformations of
![]() $S_0$
which are analytically equisingular at
$S_0$
which are analytically equisingular at
![]() $p_i$
. Hence, by Remark 3.7, the tangent space to
$p_i$
. Hence, by Remark 3.7, the tangent space to
![]() $\pi _1(\pi _2^{-1}(V_i))$
at
$\pi _1(\pi _2^{-1}(V_i))$
at
![]() $[S_0]$
is contained in
$[S_0]$
is contained in
![]() $H^0(S,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{p_i|\mathcal {X}_0})$
and
$H^0(S,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{p_i|\mathcal {X}_0})$
and
If (3.15) holds, then
![]() $h^1(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{p_i|\mathcal {X}_0})=0$
for all
$h^1(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{p_i|\mathcal {X}_0})=0$
for all
![]() $i=1,\ldots , \delta $
, and one has
$i=1,\ldots , \delta $
, and one has
Thus,
![]() $\pi _1(\pi _2^{-1}(V_i))$
, that is an open analytic subset of
$\pi _1(\pi _2^{-1}(V_i))$
, that is an open analytic subset of
![]() $\mathcal {ES}_{[S_0],p_i}^{\mathcal {X}_0}$
, is an analytic branch of U of dimension
$\mathcal {ES}_{[S_0],p_i}^{\mathcal {X}_0}$
, is an analytic branch of U of dimension
![]() $h^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0})-1$
, smooth at
$h^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0})-1$
, smooth at
![]() $[S_0]$
.
$[S_0]$
.
Next, we prove that the general element
![]() $[S_0^{\prime }]$
in
$[S_0^{\prime }]$
in
![]() $\pi _1(\pi _2^{-1}(V_i))$
has a unique
$\pi _1(\pi _2^{-1}(V_i))$
has a unique
![]() $T_1$
singularity. We argue for the case
$T_1$
singularity. We argue for the case
![]() $i=1$
, and the proof is analogous in the other cases. Suppose this is not the case, and that
$i=1$
, and the proof is analogous in the other cases. Suppose this is not the case, and that
![]() $S_0^{\prime }$
has s singularities
$S_0^{\prime }$
has s singularities
![]() $q_1,\ldots , q_s$
of type
$q_1,\ldots , q_s$
of type
![]() $T_1$
with
$T_1$
with
![]() $s>1$
. When
$s>1$
. When
![]() $S_0^{\prime }$
specializes to
$S_0^{\prime }$
specializes to
![]() $S_0$
,
$S_0$
,
![]() $q_1,\ldots , q_s$
specialize, say, to
$q_1,\ldots , q_s$
specialize, say, to
![]() $p_1,\ldots , p_s$
. By the same argument as above, the tangent space to
$p_1,\ldots , p_s$
. By the same argument as above, the tangent space to
![]() $\pi _1(\pi _2^{-1}(V_1))$
at
$\pi _1(\pi _2^{-1}(V_1))$
at
![]() $[S_0^{\prime }]$
is contained in
$[S_0^{\prime }]$
is contained in
![]() $H^0(S_0^{\prime } ,\mathcal N_{ S_0^{\prime }|\mathcal {X}_0}\otimes I_{\{q_1,\ldots , q_s\}|\mathcal {X}_0})$
and, under the hypothesis (3.15), one has
$H^0(S_0^{\prime } ,\mathcal N_{ S_0^{\prime }|\mathcal {X}_0}\otimes I_{\{q_1,\ldots , q_s\}|\mathcal {X}_0})$
and, under the hypothesis (3.15), one has
and this is a contradiction. This proves the assertion for
![]() $r=1$
.
$r=1$
.
Consider now the case
![]() $\delta>r>1$
. Fix
$\delta>r>1$
. Fix
![]() $p_{i_1},\ldots , p_{i_r}$
distinct points among
$p_{i_1},\ldots , p_{i_r}$
distinct points among
![]() $p_1,\ldots , p_\delta $
. The intersection
$p_1,\ldots , p_\delta $
. The intersection
 $$ \begin{align*}\mathfrak T_{i_1,\ldots, i_r}:=\bigcap_{j=1}^r \pi_1(\pi_2^{-1}(V_{i_j})),\end{align*} $$
$$ \begin{align*}\mathfrak T_{i_1,\ldots, i_r}:=\bigcap_{j=1}^r \pi_1(\pi_2^{-1}(V_{i_j})),\end{align*} $$
that is an analytic open subset of
![]() $\mathcal {ES}_{[S_0],p_{i_1},\ldots , p_{i_r}}^{\mathcal {X}_0}$
, is an analytic variety in
$\mathcal {ES}_{[S_0],p_{i_1},\ldots , p_{i_r}}^{\mathcal {X}_0}$
, is an analytic variety in
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
parametrizing deformations of
$\mathcal H^{\mathcal {X}_0}_{S_0}$
parametrizing deformations of
![]() $S_0$
that are analytic equisingular at the points
$S_0$
that are analytic equisingular at the points
![]() $p_{i_1},\ldots , p_{i_r}$
. With the same argument as above, one sees that, under the hypothesis (3.15),
$p_{i_1},\ldots , p_{i_r}$
. With the same argument as above, one sees that, under the hypothesis (3.15),
![]() $\mathfrak T_{i_1,\ldots , i_r}$
is smooth of codimension r in
$\mathfrak T_{i_1,\ldots , i_r}$
is smooth of codimension r in
![]() $\mathcal H_{S_0}^{\mathcal {X}_0}$
, with tangent space at
$\mathcal H_{S_0}^{\mathcal {X}_0}$
, with tangent space at
![]() $[S_0]$
given by
$[S_0]$
given by
![]() $H^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_{i_1},\dots ,p_{i_r}\}|\mathcal {X}_0})$
.
$H^0(S_0,\mathcal N_{ S_0|\mathcal {X}_0}\otimes I_{\{p_{i_1},\dots ,p_{i_r}\}|\mathcal {X}_0})$
.
Moreover, again by the same argument as above, the general element
![]() $S^{\prime }_0$
in
$S^{\prime }_0$
in
![]() $\mathfrak T_{i_1,\ldots , i_r}$
has exactly r singularities of type
$\mathfrak T_{i_1,\ldots , i_r}$
has exactly r singularities of type
![]() $T_1$
at points specializing to
$T_1$
at points specializing to
![]() $p_{i_1}, \ldots , p_{i_r}$
when
$p_{i_1}, \ldots , p_{i_r}$
when
![]() $S^{\prime }_0$
specializes to
$S^{\prime }_0$
specializes to
![]() $S_0$
. So
$S_0$
. So
![]() $\mathfrak T_{i_1,\ldots , i_r}$
is a smooth analytic branch of
$\mathfrak T_{i_1,\ldots , i_r}$
is a smooth analytic branch of
![]() $\mathbb {T}_r$
containing
$\mathbb {T}_r$
containing
![]() $[S_0]$
, and this ends the proof of the corollary.
$[S_0]$
, and this ends the proof of the corollary.
Let now
![]() $\mathbb {T}_{\delta _A,\delta _B,\delta _R}\subseteq \mathcal H^{\mathcal {X}_0}$
be the Zariski closure of the family of surfaces
$\mathbb {T}_{\delta _A,\delta _B,\delta _R}\subseteq \mathcal H^{\mathcal {X}_0}$
be the Zariski closure of the family of surfaces
![]() $S_0=S_A\cup S_B$
in
$S_0=S_A\cup S_B$
in
![]() $\mathcal {X}_0$
with
$\mathcal {X}_0$
with
![]() $\delta _A$
nodes on A and
$\delta _A$
nodes on A and
![]() $\delta _B$
nodes on B off R and
$\delta _B$
nodes on B off R and
![]() $\delta _R$
singularities of type
$\delta _R$
singularities of type
![]() $T_1$
on R.
$T_1$
on R.
Corollary 3.8.3. Let
![]() $S_0=S_A\cup S_B$
be a reduced effective Cartier divisor such that
$S_0=S_A\cup S_B$
be a reduced effective Cartier divisor such that
![]() $S_A$
and
$S_A$
and
![]() $S_B$
have, respectively,
$S_B$
have, respectively,
![]() $\delta _A$
and
$\delta _A$
and
![]() $\delta _B$
nodes
$\delta _B$
nodes
![]() $p_{A,1},\ldots , p_{A,\delta _A}$
and
$p_{A,1},\ldots , p_{A,\delta _A}$
and
![]() $p_{B,1},\ldots , p_{B,\delta _B}$
off R, are elsewhere smooth and intersect transversally along a curve
$p_{B,1},\ldots , p_{B,\delta _B}$
off R, are elsewhere smooth and intersect transversally along a curve
![]() $C=S_A\cap S_B$
, except for
$C=S_A\cap S_B$
, except for
![]() $\delta _R$
distinct points
$\delta _R$
distinct points
![]() $p_{R,1}, \ldots , p_{R,\delta _R} \in C\subset R$
where
$p_{R,1}, \ldots , p_{R,\delta _R} \in C\subset R$
where
![]() $S_0$
has singularities of type
$S_0$
has singularities of type
![]() $T_1$
. Let
$T_1$
. Let
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
be the locally closed set of equisingular deformations of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
be the locally closed set of equisingular deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
. Consider the ideal sheaf
$\mathcal {X}_0$
. Consider the ideal sheaf
![]() $I_{\mathfrak Z|\mathcal {X}_0}$
in
$I_{\mathfrak Z|\mathcal {X}_0}$
in
![]() $\mathcal {X}_0$
of the
$\mathcal {X}_0$
of the
![]() $0$
-dimensional reduced scheme
$0$
-dimensional reduced scheme
![]() $\mathfrak Z$
of lenght
$\mathfrak Z$
of lenght
![]() $\delta =\delta _A+\delta _B+\delta _R$
given by
$\delta =\delta _A+\delta _B+\delta _R$
given by
 $$ \begin{align*}\mathfrak Z= \sum_{i=1}^{\delta_A} p_{A,i}+\sum_{i=1}^{\delta_B} p_{B,i}+\sum_{i=1}^{\delta_R} p_{R,i}. \end{align*} $$
$$ \begin{align*}\mathfrak Z= \sum_{i=1}^{\delta_A} p_{A,i}+\sum_{i=1}^{\delta_B} p_{B,i}+\sum_{i=1}^{\delta_R} p_{R,i}. \end{align*} $$
Then
If
and the map
defined as in Lemma 3.4 is dominant, then the equality holds in (3.19), and the locally closed set
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
of locally trivial deformations of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
of locally trivial deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
is smooth at
$\mathcal {X}_0$
is smooth at
![]() $[S_0]$
of dimension
$[S_0]$
of dimension
![]() $h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\mathfrak Z|\mathcal {X}_0})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta $
. In particular, there exists only one irreducible component
$h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\mathfrak Z|\mathcal {X}_0})=h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta $
. In particular, there exists only one irreducible component
![]() $\mathbb {T}\subset \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
containing the point
$\mathbb {T}\subset \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
containing the point
![]() $[S_0]$
(which is smooth at
$[S_0]$
(which is smooth at
![]() $[S_0]$
and contains
$[S_0]$
and contains
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
as a Zariski open set). Moreover, under these hypotheses, the singularities of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
as a Zariski open set). Moreover, under these hypotheses, the singularities of
![]() $S_0$
may be smoothed independently in
$S_0$
may be smoothed independently in
![]() $\mathcal {X}_0$
. More precisely, for every
$\mathcal {X}_0$
. More precisely, for every
![]() $\delta _A'\leqslant \delta _A$
,
$\delta _A'\leqslant \delta _A$
,
![]() $\delta _B'\leqslant \delta _B$
and
$\delta _B'\leqslant \delta _B$
and
![]() $\delta ^{\prime }_R\leqslant \delta _R$
, we have that
$\delta ^{\prime }_R\leqslant \delta _R$
, we have that
![]() $\mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
is nonempty and
$\mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
is nonempty and
![]() $[S_0]\in \mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
. In an analytic neighborhood of
$[S_0]\in \mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
. In an analytic neighborhood of
![]() $[S_0]$
,
$[S_0]$
,
![]() $\mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
consists of
$\mathbb {T}_{\delta _A',\delta _B',\delta _R'}$
consists of
 $$ \begin{align*}{\delta_R \choose \delta^{\prime}_R}\, {\delta_A \choose \delta^{\prime}_A}\, {\delta_B \choose \delta^{\prime}_B} \end{align*} $$
$$ \begin{align*}{\delta_R \choose \delta^{\prime}_R}\, {\delta_A \choose \delta^{\prime}_A}\, {\delta_B \choose \delta^{\prime}_B} \end{align*} $$
smooth analytic branches of dimension
![]() $h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta '$
, where
$h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-\delta '$
, where
![]() $\delta '=\delta _A'+\delta _B'+\delta _R'$
, that intersect at
$\delta '=\delta _A'+\delta _B'+\delta _R'$
, that intersect at
![]() $[S_0]$
along a smooth analytic branch of
$[S_0]$
along a smooth analytic branch of
![]() $\mathbb {T}\subset \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
, corresponding to deformations of
$\mathbb {T}\subset \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
, corresponding to deformations of
![]() $[S_0]$
preserving
$[S_0]$
preserving
![]() $\delta _R'$
points of type
$\delta _R'$
points of type
![]() $T_1$
and
$T_1$
and
![]() $\delta _A'$
nodes on A and
$\delta _A'$
nodes on A and
![]() $\delta _B'$
nodes on B.
$\delta _B'$
nodes on B.
Proof. Let
![]() $S_0$
be a surface as in the statement. The inclusion (3.19) follows from Lemma 3.6, Remark 3.7 and well-known deformation theory of nodal surfaces (see [Reference Greuel and Karras11, §2.3]). It can be proved by using (3.10). In particular, if one localizes (3.10) at a node p of
$S_0$
be a surface as in the statement. The inclusion (3.19) follows from Lemma 3.6, Remark 3.7 and well-known deformation theory of nodal surfaces (see [Reference Greuel and Karras11, §2.3]). It can be proved by using (3.10). In particular, if one localizes (3.10) at a node p of
![]() $S_0$
, then
$S_0$
, then
![]() $H^0(S_0,T^1_{{S_0},p})\cong \mathbb {C}$
can be identified with the tangent space to the versal deformation space of a node.
$H^0(S_0,T^1_{{S_0},p})\cong \mathbb {C}$
can be identified with the tangent space to the versal deformation space of a node.
Now we want to prove that, under the hypotheses of the corollary, the locally closed set
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
is smooth at
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
is smooth at
![]() $[S_0]$
of codimension
$[S_0]$
of codimension
![]() $\delta $
in the Hilbert scheme
$\delta $
in the Hilbert scheme
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
.
$\mathcal H^{\mathcal {X}_0}_{S_0}$
.
Let
![]() $C\subset R$
be the
$C\subset R$
be the
![]() $\delta _R$
-nodal curve cut out by
$\delta _R$
-nodal curve cut out by
![]() $S_0$
on R. By the hypothesis (3.20), one has that
$S_0$
on R. By the hypothesis (3.20), one has that
![]() $h^1(C, \mathcal N_{C|R}\otimes \mathcal I_{\{p_{R,1}, \ldots , p_{R,\delta _R}\}|R})=0.$
This implies that
$h^1(C, \mathcal N_{C|R}\otimes \mathcal I_{\{p_{R,1}, \ldots , p_{R,\delta _R}\}|R})=0.$
This implies that
![]() $[C]$
is a smooth point of the locally closed Severi variety
$[C]$
is a smooth point of the locally closed Severi variety
![]() $\mathcal V_\delta $
of
$\mathcal V_\delta $
of
![]() $\delta $
-nodal curves in
$\delta $
-nodal curves in
![]() $\mathcal H^R_C$
. Let V be the unique irreducible component of
$\mathcal H^R_C$
. Let V be the unique irreducible component of
![]() $\mathcal V_\delta $
containing
$\mathcal V_\delta $
containing
![]() $[C]$
. Now, as we saw in Lemma 3.4,
$[C]$
. Now, as we saw in Lemma 3.4,
![]() $ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
has at least one irreducible component of codimension at most
$ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
has at least one irreducible component of codimension at most
![]() $\delta _R$
in
$\delta _R$
in
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
. However, by Lemma 3.6, we have that
$\mathcal H^{\mathcal {X}_0}_{S_0}$
. However, by Lemma 3.6, we have that
and by (3.20), we have
![]() $h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\{p_{R,1}, \ldots , p_{R,\delta _R}\}|\mathcal {X}_0})=\dim (\mathcal H^{\mathcal {X}_0}_{S_0})-\delta _R$
. Thus,
$h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\{p_{R,1}, \ldots , p_{R,\delta _R}\}|\mathcal {X}_0})=\dim (\mathcal H^{\mathcal {X}_0}_{S_0})-\delta _R$
. Thus,
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is smooth at
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is smooth at
![]() $[S_0]$
of codimension
$[S_0]$
of codimension
![]() $\delta _R$
. We observe that
$\delta _R$
. We observe that
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is an analytic open set of the variety
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is an analytic open set of the variety
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}}$
of deformations of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}}$
of deformations of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
that are locally trivial at every
$\mathcal {X}_0$
that are locally trivial at every
![]() $T_1$
singularity
$T_1$
singularity
![]() $p_{R,i}$
, and we just proved that
$p_{R,i}$
, and we just proved that
We morever observe that the general element
![]() $[S^{\prime }_0]$
of
$[S^{\prime }_0]$
of
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
corresponds to a surface
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
corresponds to a surface
![]() $S^{\prime }_0=S^{\prime }_A\cup S^{\prime }_B$
, where
$S^{\prime }_0=S^{\prime }_A\cup S^{\prime }_B$
, where
![]() $S^{\prime }_A$
and
$S^{\prime }_A$
and
![]() $S^{\prime }_B$
intersect transversally along a curve
$S^{\prime }_B$
intersect transversally along a curve
![]() $C'$
on R, except for
$C'$
on R, except for
![]() $\delta _R$
points
$\delta _R$
points
![]() $p_{R,1}', \ldots , p_{R,\delta _R}'\in C'$
, which are singularities of type
$p_{R,1}', \ldots , p_{R,\delta _R}'\in C'$
, which are singularities of type
![]() $T_1$
of
$T_1$
of
![]() $S^{\prime }_0$
, and specialize to
$S^{\prime }_0$
, and specialize to
![]() $p_{R,1}, \ldots , p_{R,\delta _R}$
as
$p_{R,1}, \ldots , p_{R,\delta _R}$
as
![]() $S_0^{\prime }$
specializies to
$S_0^{\prime }$
specializies to
![]() $S_0$
.
$S_0$
.
We claim that
![]() $S_A'$
and
$S_A'$
and
![]() $S_B'$
are smooth outside R. Indeed, since
$S_B'$
are smooth outside R. Indeed, since
![]() $[S_0]$
belongs to
$[S_0]$
belongs to
![]() $ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
, the surface
$ \varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
, the surface
![]() $S^{\prime }_0$
may have at most
$S^{\prime }_0$
may have at most
![]() $\delta ^{\prime }_A\leqslant \delta _A$
nodes
$\delta ^{\prime }_A\leqslant \delta _A$
nodes
![]() $p_{A,1},\ldots , p_{A,\delta ^{\prime }_A}$
on A and
$p_{A,1},\ldots , p_{A,\delta ^{\prime }_A}$
on A and
![]() $\delta ^{\prime }_B\leqslant \delta _B$
nodes
$\delta ^{\prime }_B\leqslant \delta _B$
nodes
![]() $p_{B,1},\ldots , p_{B,\delta ^{\prime }_B}$
on B, deformations of
$p_{B,1},\ldots , p_{B,\delta ^{\prime }_B}$
on B, deformations of
![]() $\delta _A'$
nodes of
$\delta _A'$
nodes of
![]() $S_0$
on A and
$S_0$
on A and
![]() $\delta _B'$
nodes of
$\delta _B'$
nodes of
![]() $S_0$
on B. If this happens, denoting by
$S_0$
on B. If this happens, denoting by
![]() $\mathfrak Z'$
the scheme of singular points of
$\mathfrak Z'$
the scheme of singular points of
![]() $S^{\prime }_0$
, then
$S^{\prime }_0$
, then
![]() $ T_{[S^{\prime }_0]}(\mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}})=T_{[S^{\prime }_0]}\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)\subseteq H^0(S^{\prime }_0,\mathcal N_{S^{\prime }_0|\mathcal {X}_0}\otimes I_{\mathfrak Z'|\mathcal {X}_0}). $
But, once again by (3.20) and by semicontinuity, one has that
$ T_{[S^{\prime }_0]}(\mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}})=T_{[S^{\prime }_0]}\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)\subseteq H^0(S^{\prime }_0,\mathcal N_{S^{\prime }_0|\mathcal {X}_0}\otimes I_{\mathfrak Z'|\mathcal {X}_0}). $
But, once again by (3.20) and by semicontinuity, one has that
![]() $h^0(S_0^{\prime },\mathcal N_{S_0^{\prime }|\mathcal {X}_0}\otimes I_{\mathfrak Z'|\mathcal {X}_0})= H^0(S^{\prime }_0,\mathcal N_{S^{\prime }_0|\mathcal {X}_0})-\delta _R-\delta ^{\prime }_A-\delta _B'.$
It follows that
$h^0(S_0^{\prime },\mathcal N_{S_0^{\prime }|\mathcal {X}_0}\otimes I_{\mathfrak Z'|\mathcal {X}_0})= H^0(S^{\prime }_0,\mathcal N_{S^{\prime }_0|\mathcal {X}_0})-\delta _R-\delta ^{\prime }_A-\delta _B'.$
It follows that
![]() $\delta ^{\prime }_A=\delta _B'=0$
(i.e.,
$\delta ^{\prime }_A=\delta _B'=0$
(i.e.,
![]() $S^{\prime }_A$
and
$S^{\prime }_A$
and
![]() $S^{\prime }_B$
are smooth off R and
$S^{\prime }_B$
are smooth off R and
![]() $\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is a locally closed set in one irreducible component
$\varphi _{|\mathcal H^{\mathcal {X}_0}_{S_0}}^{-1}(V)$
is a locally closed set in one irreducible component
![]() $\mathbb {T}\subset \mathbb {T}_{\delta _R}$
, smooth at
$\mathbb {T}\subset \mathbb {T}_{\delta _R}$
, smooth at
![]() $[S_0]$
). We just proved that, under our hypotheses, one may deform
$[S_0]$
). We just proved that, under our hypotheses, one may deform
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
by smoothing all nodes of
$\mathcal {X}_0$
by smoothing all nodes of
![]() $S_0$
and by preserving all
$S_0$
and by preserving all
![]() $T_1$
singularities.
$T_1$
singularities.
Let now
![]() $\mathfrak Z_A$
and
$\mathfrak Z_A$
and
![]() $\mathfrak Z_B$
be, respectively, the scheme of nodes of
$\mathfrak Z_B$
be, respectively, the scheme of nodes of
![]() $S_0$
on A and B. Let
$S_0$
on A and B. Let
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
be the scheme of deformations of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
be the scheme of deformations of
![]() $S_0$
which are locally trivial at every node of
$S_0$
which are locally trivial at every node of
![]() $S_0$
. By standard deformation theory of nodal surfaces, one has that, under the hypothesis
$S_0$
. By standard deformation theory of nodal surfaces, one has that, under the hypothesis
![]() $h^1(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal {X}_0})=0$
(that holds by (3.20)),
$h^1(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal {X}_0})=0$
(that holds by (3.20)),
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is smooth of codimension
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is smooth of codimension
![]() $\delta _A+\delta _B$
in
$\delta _A+\delta _B$
in
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
at
$\mathcal H^{\mathcal {X}_0}_{S_0}$
at
![]() $[S_0]$
, and moreover,
$[S_0]$
, and moreover,
With a similar argument as above, one sees that the general element
![]() $[\tilde S_0]$
of
$[\tilde S_0]$
of
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
corresponds to a surface
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
corresponds to a surface
![]() $\tilde S_0=\tilde S_A\cup \tilde S_B$
, with
$\tilde S_0=\tilde S_A\cup \tilde S_B$
, with
![]() $\tilde S_A$
and
$\tilde S_A$
and
![]() $\tilde S_B$
intersecting transversally along a smooth curve
$\tilde S_B$
intersecting transversally along a smooth curve
![]() $\tilde C\subset R$
and having, respectively,
$\tilde C\subset R$
and having, respectively,
![]() $\delta _A$
and
$\delta _A$
and
![]() $\delta _B$
nodes as singularities. In particular,
$\delta _B$
nodes as singularities. In particular,
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is a locally closed set in an irreducible component
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is a locally closed set in an irreducible component
![]() $\tilde {\mathbb {T}}$
of
$\tilde {\mathbb {T}}$
of
![]() $\mathbb {T}_{\delta _A,\delta _B,0}$
, of which
$\mathbb {T}_{\delta _A,\delta _B,0}$
, of which
![]() $[S_0]$
is a smooth point.
$[S_0]$
is a smooth point.
Now the equisingular deformation locus
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
of
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
of
![]() $S_0$
in
$S_0$
in
![]() $\mathcal {X}_0$
is the intersection of the loci
$\mathcal {X}_0$
is the intersection of the loci
![]() $ \mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}}$
and
$ \mathcal {ES}^{\mathcal {X}_0}_{[S_0],p_{R,1}, \ldots , p_{R,\delta _R}}$
and
![]() $ \mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
. Hence,
$ \mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
. Hence,
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
has codimension at most
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
has codimension at most
![]() $\delta $
in
$\delta $
in
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
because
$\mathcal H^{\mathcal {X}_0}_{S_0}$
because
![]() $[S_0]$
is a smooth point of
$[S_0]$
is a smooth point of
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
.
$\mathcal H^{\mathcal {X}_0}_{S_0}$
.
However, one has
 $$ \begin{align*} T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0]}) & = T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0],p_{R,1}, \ldots, p_{R,\delta_R}})\cap T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B})\\ & = H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\{p_{R,1}, \ldots, p_{R,\delta_R}\}|\mathcal{X}_0}) \cap H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal{X}_0})\\ & = H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\mathfrak Z|\mathcal{X}_0}). \end{align*} $$
$$ \begin{align*} T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0]}) & = T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0],p_{R,1}, \ldots, p_{R,\delta_R}})\cap T_{[S_0]}(\mathcal {ES}^{\mathcal{X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B})\\ & = H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\{p_{R,1}, \ldots, p_{R,\delta_R}\}|\mathcal{X}_0}) \cap H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal{X}_0})\\ & = H^0(S_0, \mathcal N_{S_0|\mathcal{X}_0}\otimes \mathcal I_{\mathfrak Z|\mathcal{X}_0}). \end{align*} $$
By (3.20), we have
This proves that
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
is smooth at
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0]}$
is smooth at
![]() $[S_0]$
of codimension exactly
$[S_0]$
of codimension exactly
![]() $\delta $
in
$\delta $
in
![]() $\mathcal H^{\mathcal {X}_0}_{S_0}$
, as wanted. This proves the first part of the corollary.
$\mathcal H^{\mathcal {X}_0}_{S_0}$
, as wanted. This proves the first part of the corollary.
The second part is proved with analogous arguments as the ones used in the proof of Corollary 3.8.2.
Proposition 3.9. Let
![]() $S_0=S_A\cup S_B$
be a reduced effective Cartier divisor as in the statement of Corollary 3.8.3. Assume that
$S_0=S_A\cup S_B$
be a reduced effective Cartier divisor as in the statement of Corollary 3.8.3. Assume that
![]() $[S_0]$
belongs to an irreducible component
$[S_0]$
belongs to an irreducible component
![]() $\mathcal H$
of
$\mathcal H$
of
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
![]() $\mathbb {D}$
and that (3.20) holds.
$\mathbb {D}$
and that (3.20) holds.
Let
![]() $\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
be the locus in
$\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
be the locus in
![]() $\mathcal H^{\mathcal {X}}$
of deformations of
$\mathcal H^{\mathcal {X}}$
of deformations of
![]() $S_0$
which are equisingular at every node of
$S_0$
which are equisingular at every node of
![]() $S_0$
. Then
$S_0$
. Then
![]() $\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is generically smooth of codimension
$\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
is generically smooth of codimension
![]() $\delta _A+\delta _B$
in
$\delta _A+\delta _B$
in
![]() $\mathcal H$
, and it contains
$\mathcal H$
, and it contains
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
as a subscheme of codimension 1.
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
as a subscheme of codimension 1.
In simple words,
![]() $[S_0]$
can be deformed out of
$[S_0]$
can be deformed out of
![]() $\mathcal {X}_0$
preserving the
$\mathcal {X}_0$
preserving the
![]() $\delta _A+\delta _B$
nodes.
$\delta _A+\delta _B$
nodes.
Proof. From the hypotheses, it follows that
![]() $H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then, by Corollary 3.8.1,
$H^1(S_0,\mathcal N_{S_0|\mathcal {X}_0})=0$
. Then, by Corollary 3.8.1,
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
is smooth at
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
is smooth at
![]() $[S_0]$
with dimension
$[S_0]$
with dimension
![]() $h^0(S_0,\mathcal N_{S_0|\mathcal {X}_0})+1=\dim (\mathcal H_{S_0}^{\mathcal {X}_0})+1$
. By standard deformation theory, there is an analytic neighborhood U of
$h^0(S_0,\mathcal N_{S_0|\mathcal {X}_0})+1=\dim (\mathcal H_{S_0}^{\mathcal {X}_0})+1$
. By standard deformation theory, there is an analytic neighborhood U of
![]() $[S_0]$
in
$[S_0]$
in
![]() $\mathcal H$
and a versal morphism
$\mathcal H$
and a versal morphism
where
![]() $\Delta _p$
is the versal deformation space of a node, and therefore, it has dimension 1. Let
$\Delta _p$
is the versal deformation space of a node, and therefore, it has dimension 1. Let
![]() $U'=U\cap \mathcal H_{S_0}^{\mathcal {X}_0}$
. Then f restricts to
$U'=U\cap \mathcal H_{S_0}^{\mathcal {X}_0}$
. Then f restricts to
The differential of g at
![]() $[S_0]$
is
$[S_0]$
is
and this map is surjective since its kernel is
![]() $H^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal {X}_0})$
, which has codimension
$H^0(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes \mathcal I_{\mathfrak Z_A\cup \mathfrak Z_B|\mathcal {X}_0})$
, which has codimension
![]() $\delta _A+\delta _B$
in
$\delta _A+\delta _B$
in
![]() $H^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})$
by (3.20). Hence, g has maximal rank at
$H^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})$
by (3.20). Hence, g has maximal rank at
![]() $[S_0]$
and therefore also f is of maximal rank at
$[S_0]$
and therefore also f is of maximal rank at
![]() $[S_0]$
. Hence,
$[S_0]$
. Hence,
![]() $f^{-1}(0)$
and
$f^{-1}(0)$
and
![]() $g^{-1}(0)$
are analytic subvarieties of U and
$g^{-1}(0)$
are analytic subvarieties of U and
![]() $U'$
, respectively, smooth at
$U'$
, respectively, smooth at
![]() $[S_0]$
and of codimension
$[S_0]$
and of codimension
![]() $\delta _A+\delta _B$
in U and
$\delta _A+\delta _B$
in U and
![]() $U'$
, respectively. By versality,
$U'$
, respectively. By versality,
![]() $f^{-1}(0)$
(resp.
$f^{-1}(0)$
(resp.
![]() $g^{-1}(0)$
) coincides with
$g^{-1}(0)$
) coincides with
![]() $\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
(resp.
$\mathcal {ES}^{\mathcal {X}}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
(resp.
![]() $\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
). The statement follows.
$\mathcal {ES}^{\mathcal {X}_0}_{[S_0],\mathfrak Z_A,\mathfrak Z_B}$
). The statement follows.
3.2.3. Global deformations of surfaces with
 $T_1$
singularities to nodal surfaces
$T_1$
singularities to nodal surfaces
In this section, we will assume the following setup. We have the family
![]() $\pi : \mathcal {X}\to \mathbb {D}$
as usual with its relative Hilbert scheme
$\pi : \mathcal {X}\to \mathbb {D}$
as usual with its relative Hilbert scheme
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
, whose fibre over
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
, whose fibre over
![]() $t\in \mathbb {D}$
is the Hilbert scheme of
$t\in \mathbb {D}$
is the Hilbert scheme of
![]() $\mathcal H^{\mathcal {X}_t}$
of
$\mathcal H^{\mathcal {X}_t}$
of
![]() $\mathcal {X}_t$
.
$\mathcal {X}_t$
.
Let
![]() $\mathcal V_\delta ^{\mathcal {X}|\mathbb {D}}$
be the Zariski closure in
$\mathcal V_\delta ^{\mathcal {X}|\mathbb {D}}$
be the Zariski closure in
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
of the relative Severi variety
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
of the relative Severi variety
![]() $\mathcal W^{\mathcal {X}\setminus \mathcal {X}_0|\mathbb {D}\setminus 0}_\delta \subset \mathcal H^{\mathcal {X}\setminus \mathcal {X}_0|\mathbb {D}\setminus 0}$
of
$\mathcal W^{\mathcal {X}\setminus \mathcal {X}_0|\mathbb {D}\setminus 0}_\delta \subset \mathcal H^{\mathcal {X}\setminus \mathcal {X}_0|\mathbb {D}\setminus 0}$
of
![]() $\delta $
-nodal surfaces. We want to provide sufficient conditions for
$\delta $
-nodal surfaces. We want to provide sufficient conditions for
![]() $\mathcal V_\delta ^{\mathcal {X}|\mathbb {D}}$
to be nonempty.
$\mathcal V_\delta ^{\mathcal {X}|\mathbb {D}}$
to be nonempty.
We will suppose that we have a line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() $\mathcal {X}$
with the following properties:
$\mathcal {X}$
with the following properties:
-
(1)
 $h^0(\mathcal {X}_t, \mathcal L_t)$
is a constant
$h^0(\mathcal {X}_t, \mathcal L_t)$
is a constant
 $r+1$
in t and greater or equal than 4. In particular, every surface
$r+1$
in t and greater or equal than 4. In particular, every surface
 $S_0$
in
$S_0$
in
 $ |\mathcal L_0|$
belongs to an irreducible component
$ |\mathcal L_0|$
belongs to an irreducible component
 $\mathcal H$
of the relative Hilbert scheme
$\mathcal H$
of the relative Hilbert scheme
 $\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
that dominates
 $\mathbb {D}$
;
$\mathbb {D}$
; -
(2)
 $|\mathcal L_0|$
is base point free, so that we can assume that
$|\mathcal L_0|$
is base point free, so that we can assume that
 $|\mathcal L_t|$
is base point free for all
$|\mathcal L_t|$
is base point free for all
 $t\in \mathbb {D}$
;
$t\in \mathbb {D}$
; -
(3) if
 $p_t\in \mathcal {X}_t$
is a general point, then the general surface in
$p_t\in \mathcal {X}_t$
is a general point, then the general surface in
 $|\mathcal L_t|$
with a singular point at
$|\mathcal L_t|$
with a singular point at
 $p_t$
is singular only at finitely many points, for the general
$p_t$
is singular only at finitely many points, for the general
 $t\in \mathbb {D}$
.
$t\in \mathbb {D}$
.
In this setting, we can consider the rank r projective bundle
![]() $\bar \pi : \mathbb {P}(\pi _*(\mathcal L))\to \mathbb {D}$
. A point in
$\bar \pi : \mathbb {P}(\pi _*(\mathcal L))\to \mathbb {D}$
. A point in
![]() $\mathbb {P}:=\mathbb {P}(\pi _*(\mathcal L))$
that maps to
$\mathbb {P}:=\mathbb {P}(\pi _*(\mathcal L))$
that maps to
![]() $t\in \mathbb {D}$
is a nonzero section of
$t\in \mathbb {D}$
is a nonzero section of
![]() $H^0(\mathcal {X}_t, \mathcal L_t)$
up to a constant. In particular, if
$H^0(\mathcal {X}_t, \mathcal L_t)$
up to a constant. In particular, if
![]() $t\neq 0$
, a point in
$t\neq 0$
, a point in
![]() $\mathbb {P}$
corresponds to a surface in
$\mathbb {P}$
corresponds to a surface in
![]() $|\mathcal L_t|$
. Consider the open Zariski subset
$|\mathcal L_t|$
. Consider the open Zariski subset
![]() $\mathbb {P}':=\bar \pi ^{-1}(\mathbb {D}\setminus \{0\})$
, which, by the above considerations, can be regarded as a subvariety of the relative Hilbert scheme of surfaces in
$\mathbb {P}':=\bar \pi ^{-1}(\mathbb {D}\setminus \{0\})$
, which, by the above considerations, can be regarded as a subvariety of the relative Hilbert scheme of surfaces in
![]() $\mathcal {X}$
. By a standard parameter count, one sees that there is a subscheme Z of pure codimension 1 in
$\mathcal {X}$
. By a standard parameter count, one sees that there is a subscheme Z of pure codimension 1 in
![]() $\mathbb {P}'$
whose points correspond to sections vanishing along singular surfaces. We will denote by
$\mathbb {P}'$
whose points correspond to sections vanishing along singular surfaces. We will denote by
![]() $\bar Z$
the closure of Z in
$\bar Z$
the closure of Z in
![]() $\mathbb {P}$
that has also codimension 1.
$\mathbb {P}$
that has also codimension 1.
Proposition 3.10. Set up as above with the following further condition: the subspace of sections of
![]() $H^0(\mathcal {X}_0,\mathcal L_0)$
that vanish on
$H^0(\mathcal {X}_0,\mathcal L_0)$
that vanish on
![]() $R=A\cap B$
, with A and B the irreducible components of
$R=A\cap B$
, with A and B the irreducible components of
![]() $\mathcal {X}_0$
, has codimension strictly larger than 1 in
$\mathcal {X}_0$
, has codimension strictly larger than 1 in
![]() $H^0(\mathcal {X}_0,\mathcal L_0)$
.
$H^0(\mathcal {X}_0,\mathcal L_0)$
.
Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a surface corresponding to a section of
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a surface corresponding to a section of
![]() $\mathcal L_0$
. We suppose that:
$\mathcal L_0$
. We suppose that:
-
(a)
 $S_A$
and
$S_A$
and
 $S_B$
are smooth and intersect transversally along a curve
$S_B$
are smooth and intersect transversally along a curve
 $C=S_A\cap S_B$
, except for a point
$C=S_A\cap S_B$
, except for a point
 $p=p_1\in C\subset R$
where
$p=p_1\in C\subset R$
where
 $S_0$
has a singularity of type
$S_0$
has a singularity of type
 $T_1$
and the hypotheses of Lemma 3.4 hold for
$T_1$
and the hypotheses of Lemma 3.4 hold for
 $\delta =1$
;
$\delta =1$
; -
(b) the sublinear system
 $\mathcal L_0(2,p)$
of
$\mathcal L_0(2,p)$
of
 $|\mathcal L_0|$
of surfaces with at least a
$|\mathcal L_0|$
of surfaces with at least a
 $T_1$
singularity at p has codimension 3 in
$T_1$
singularity at p has codimension 3 in
 $|\mathcal L_0|$
;
$|\mathcal L_0|$
; -
(c) (3.15) (for
 $\delta =1$
) holds for
$\delta =1$
) holds for
 $S_0$
.
$S_0$
.
Then:
-
(i)
 $\mathbb {T}_1$
is smooth at
$\mathbb {T}_1$
is smooth at
 $[S_0]$
of codimension
$[S_0]$
of codimension
 $1$
in
$1$
in
 $\mathcal H_0$
;
$\mathcal H_0$
; -
(ii)
 $S_0$
can be deformed to a
$S_0$
can be deformed to a
 $1$
-nodal surface
$1$
-nodal surface
 $S_t\subset \mathcal {X}_t$
;
$S_t\subset \mathcal {X}_t$
; -
(iii) if
 $\mathbb {T}\subseteq \mathbb {T}_1$
is the unique irreducible component containing
$\mathbb {T}\subseteq \mathbb {T}_1$
is the unique irreducible component containing
 $[S_0]$
, then there exists a reduced, irreducible component
$[S_0]$
, then there exists a reduced, irreducible component
 $\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_1$
of dimension
$\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_1$
of dimension
 $\dim (\mathcal H)-1$
whose central fibre
$\dim (\mathcal H)-1$
whose central fibre
 $\mathcal V_0$
contains
$\mathcal V_0$
contains
 $\mathbb {T}$
as an irreducible component.
$\mathbb {T}$
as an irreducible component.
Before giving the proof of the proposition, we make a preliminary lemma. For this, we need some notation. Let
![]() $I\subset |\mathcal L_0|\times R$
, with
$I\subset |\mathcal L_0|\times R$
, with
![]() $R=A\cap B$
be the locally closed subset consisting of pairs
$R=A\cap B$
be the locally closed subset consisting of pairs
![]() $(S_0,p)$
such that
$(S_0,p)$
such that
![]() $S_0$
cuts out on R a curve singular at p. We will consider the two projections
$S_0$
cuts out on R a curve singular at p. We will consider the two projections
![]() $\pi _1: I\to |\mathcal L_0|$
and
$\pi _1: I\to |\mathcal L_0|$
and
![]() $\pi _2: I\to R$
. Note that if
$\pi _2: I\to R$
. Note that if
![]() $p\in R$
, then
$p\in R$
, then
![]() $\pi _2^{-1}(p)$
can be identified with
$\pi _2^{-1}(p)$
can be identified with
![]() $\mathcal L_0(2,p)$
.
$\mathcal L_0(2,p)$
.
Lemma 3.11.
(i) There is at most one irreducible component
![]() $I'$
of I such that the restriction of
$I'$
of I such that the restriction of
![]() $\pi _2$
to
$\pi _2$
to
![]() $I'$
is dominant to R via
$I'$
is dominant to R via
![]() $\pi _2$
.
$\pi _2$
.
(ii) If
![]() $I'$
exists, and if its general element
$I'$
exists, and if its general element
![]() $(S_0,p)$
is such that
$(S_0,p)$
is such that
![]() $S_0$
cuts out on R a curve with finitely many singular points, then
$S_0$
cuts out on R a curve with finitely many singular points, then
![]() $\mathcal L_0(2,p)$
has codimension 3 in
$\mathcal L_0(2,p)$
has codimension 3 in
![]() $|\mathcal L_0|$
. Moreover,
$|\mathcal L_0|$
. Moreover,
![]() $\dim (I')= \dim (|\mathcal L_0|)-1$
, and its image in
$\dim (I')= \dim (|\mathcal L_0|)-1$
, and its image in
![]() $|\mathcal L_0|$
via
$|\mathcal L_0|$
via
![]() $\pi _1$
has codimension 1 in
$\pi _1$
has codimension 1 in
![]() $|\mathcal L_0|$
.
$|\mathcal L_0|$
.
(iii) If there is a pair
![]() $(S_0,p)$
in I such that
$(S_0,p)$
in I such that
![]() $S_0$
cuts out on R a curve with finitely many singular points and if
$S_0$
cuts out on R a curve with finitely many singular points and if
![]() $ \mathcal L_0(2,p)$
has codimension 3 in
$ \mathcal L_0(2,p)$
has codimension 3 in
![]() $|\mathcal L_0|$
, then
$|\mathcal L_0|$
, then
![]() $(S_0,p)$
belongs to an irreducible component
$(S_0,p)$
belongs to an irreducible component
![]() $I'$
of I dominating R via
$I'$
of I dominating R via
![]() $\pi _2$
. For this component, one has
$\pi _2$
. For this component, one has
![]() $\dim (I')= \dim (|\mathcal L_0|)-1$
, and its image in
$\dim (I')= \dim (|\mathcal L_0|)-1$
, and its image in
![]() $|\mathcal L_0|$
via
$|\mathcal L_0|$
via
![]() $\pi _1$
has codimension 1 in
$\pi _1$
has codimension 1 in
![]() $|\mathcal L_0|$
.
$|\mathcal L_0|$
.
Proof. (i) Let
![]() $I'$
be an irreducible component of I such that
$I'$
be an irreducible component of I such that
![]() $I'$
is dominant to R via
$I'$
is dominant to R via
![]() $\pi _2$
. If
$\pi _2$
. If
![]() $p\in R$
is a general point, we know that
$p\in R$
is a general point, we know that
![]() $\pi _2^{-1}(p)$
can be identified with
$\pi _2^{-1}(p)$
can be identified with
![]() $\mathcal L_0(2,p)$
, and
$\mathcal L_0(2,p)$
, and
![]() $\mathcal L_0(2,p)$
is a projective space with dimension s independent on the general point p. This clearly implies that
$\mathcal L_0(2,p)$
is a projective space with dimension s independent on the general point p. This clearly implies that
![]() $I'$
is unique.
$I'$
is unique.
(ii) Suppose the dominating component
![]() $I'$
exists. With the same notation as above, we have
$I'$
exists. With the same notation as above, we have
![]() $\dim (I')=\dim (R)+s=s+2$
. However, by Remark 2.4,
$\dim (I')=\dim (R)+s=s+2$
. However, by Remark 2.4,
![]() $s\geqslant \dim (|\mathcal L_0|)-3$
; hence,
$s\geqslant \dim (|\mathcal L_0|)-3$
; hence,
![]() $\dim (I')\geqslant \dim (|\mathcal L_0|)-1$
. By the hypotheses, the map
$\dim (I')\geqslant \dim (|\mathcal L_0|)-1$
. By the hypotheses, the map
![]() $\pi _1$
, restricted to
$\pi _1$
, restricted to
![]() $I'$
, is generically finite onto the image, and this image cannot be dense in
$I'$
, is generically finite onto the image, and this image cannot be dense in
![]() $|\mathcal L_0|$
by Bertini’s theorem. Hence,
$|\mathcal L_0|$
by Bertini’s theorem. Hence,
![]() $\dim (I')\leqslant \dim (|\mathcal L_0|)-1$
, so the equality holds, and this implies that
$\dim (I')\leqslant \dim (|\mathcal L_0|)-1$
, so the equality holds, and this implies that
![]() $s=\dim (|\mathcal L_0|)-3$
, as wanted.
$s=\dim (|\mathcal L_0|)-3$
, as wanted.
(iii) Keep the same notation as above. The dimension of the fibre of
![]() $\pi _2$
over a general point of R is
$\pi _2$
over a general point of R is
![]() $r\geqslant \dim (|\mathcal L_0|)-3= \mathcal L_0(2,p)\geqslant 0$
. Moreover, there is an open dense subset U of R, containing p, such that for all
$r\geqslant \dim (|\mathcal L_0|)-3= \mathcal L_0(2,p)\geqslant 0$
. Moreover, there is an open dense subset U of R, containing p, such that for all
![]() $q\in U$
, one has that
$q\in U$
, one has that
![]() $\mathcal L_0(2,p)$
has dimension
$\mathcal L_0(2,p)$
has dimension
![]() $ s = \dim (|\mathcal L_0|)-3$
. Hence, there is a component
$ s = \dim (|\mathcal L_0|)-3$
. Hence, there is a component
![]() $I'$
of I dominating R via
$I'$
of I dominating R via
![]() $\pi _2$
.
$\pi _2$
.
We can now give the following:
Proof of Proposition 3.10
We notice that by Corollary 3.8.1,
![]() $[S_0]$
is a smooth point for
$[S_0]$
is a smooth point for
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
. Part (i) follows by Corollary 3.7.1.
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
. Part (i) follows by Corollary 3.7.1.
Let us prove part (ii). For this, we go back to the notation introduced before the statement of Proposition 3.10. Consider then the intersection
![]() $\bar Z_0$
of
$\bar Z_0$
of
![]() $\bar Z$
with
$\bar Z$
with
![]() $\bar \pi ^{-1}(0)\cong |\mathcal L_0|$
, such that any of its irreducible components has codimension 1 in
$\bar \pi ^{-1}(0)\cong |\mathcal L_0|$
, such that any of its irreducible components has codimension 1 in
![]() $|\mathcal L_0|$
. By the hypotheses we made, if
$|\mathcal L_0|$
. By the hypotheses we made, if
![]() $\bar Z^{\prime }_0$
is any irreducible component of
$\bar Z^{\prime }_0$
is any irreducible component of
![]() $\bar Z_0$
, its general element does not contain R; hence, it is a surface
$\bar Z_0$
, its general element does not contain R; hence, it is a surface
![]() $S_0^{\prime }\in |\mathcal L_0|$
that intersects R along a curve
$S_0^{\prime }\in |\mathcal L_0|$
that intersects R along a curve
![]() $C'$
. By Proposition 3.1, the curve
$C'$
. By Proposition 3.1, the curve
![]() $C'$
is singular.
$C'$
is singular.
Claim 3.12. There is an irreducible component
![]() $\bar Z^{\prime }_0$
of
$\bar Z^{\prime }_0$
of
![]() $\bar Z_0$
, such that for
$\bar Z_0$
, such that for
![]() $S_0^{\prime }\in \bar Z^{\prime }_0$
general,
$S_0^{\prime }\in \bar Z^{\prime }_0$
general,
![]() $S_0^{\prime }$
intersects R in a curve
$S_0^{\prime }$
intersects R in a curve
![]() $C'$
that is singular at a general point
$C'$
that is singular at a general point
![]() $p'$
of R. Moreover,
$p'$
of R. Moreover,
![]() $S_0^{\prime }$
is limit of reduced singular surfaces
$S_0^{\prime }$
is limit of reduced singular surfaces
![]() $S_t\in |\mathcal L_t|$
.
$S_t\in |\mathcal L_t|$
.
Proof of the Claim 3.12
This will be a consequence of the following fact that we are going to prove: given a general point
![]() $p'\in R$
, there is some
$p'\in R$
, there is some
![]() $S_0^{\prime }\in \bar Z_0$
such that the curve
$S_0^{\prime }\in \bar Z_0$
such that the curve
![]() $C'$
cut out by
$C'$
cut out by
![]() $S_0^{\prime }$
on R is singular at
$S_0^{\prime }$
on R is singular at
![]() $p'$
. Indeed, given
$p'$
. Indeed, given
![]() $p'\in R$
general, take a smooth bisection
$p'\in R$
general, take a smooth bisection
![]() $\gamma '$
of
$\gamma '$
of
![]() $\mathcal {X}\to \mathbb {D}$
that passes through
$\mathcal {X}\to \mathbb {D}$
that passes through
![]() $p'$
. As in §2.1, we can consider the family
$p'$
. As in §2.1, we can consider the family
![]() $\mathcal Y\to \mathbb {D}$
obtained by desingularising the variety
$\mathcal Y\to \mathbb {D}$
obtained by desingularising the variety
![]() $\mathcal {X}'\to \mathbb {D}$
gotten via 2-fold base change
$\mathcal {X}'\to \mathbb {D}$
gotten via 2-fold base change
![]() $\nu _2: \mathbb {D}\to \mathbb {D}$
. The variety
$\nu _2: \mathbb {D}\to \mathbb {D}$
. The variety
![]() $\mathcal Y\to \mathbb {D}$
has a section
$\mathcal Y\to \mathbb {D}$
has a section
![]() $\gamma $
that is mapped to
$\gamma $
that is mapped to
![]() $\gamma '$
via the map
$\gamma '$
via the map
![]() $\pi : \mathcal Y\to \mathcal {X}$
. We consider
$\pi : \mathcal Y\to \mathcal {X}$
. We consider
![]() $\pi ^{*}(\mathcal L)$
. Our assumption (3) implies that there are nonzero sections of
$\pi ^{*}(\mathcal L)$
. Our assumption (3) implies that there are nonzero sections of
![]() $\pi ^{*}(\mathcal L)$
, on
$\pi ^{*}(\mathcal L)$
, on
![]() $\mathcal Y\setminus \mathcal Y_0$
, vanishing with multiplicity at least 2 along
$\mathcal Y\setminus \mathcal Y_0$
, vanishing with multiplicity at least 2 along
![]() $\gamma $
. The assertion is now a consequence of Theorem 2.2.
$\gamma $
. The assertion is now a consequence of Theorem 2.2.
By the hypothesis (b) and by Lemma 3.11(iii), the pair
![]() $(S_0,p)$
belongs to the unique irreducible component
$(S_0,p)$
belongs to the unique irreducible component
![]() $I'$
of I dominating R via
$I'$
of I dominating R via
![]() $\pi _2$
, and
$\pi _2$
, and
![]() $I'$
has dimension equal to
$I'$
has dimension equal to
![]() $\dim (|\mathcal L_0|)-1$
. Consider now the subset
$\dim (|\mathcal L_0|)-1$
. Consider now the subset
![]() $I"\subseteq I$
of the pairs
$I"\subseteq I$
of the pairs
![]() $(S_0^{\prime },p')$
with
$(S_0^{\prime },p')$
with
![]() $S_0^{\prime }\in \bar Z^{\prime }_0$
, where
$S_0^{\prime }\in \bar Z^{\prime }_0$
, where
![]() $\bar Z^{\prime }_0$
is as in Claim 3.12. We notice that
$\bar Z^{\prime }_0$
is as in Claim 3.12. We notice that
![]() $I"$
also dominates R via
$I"$
also dominates R via
![]() $\pi _2$
. So by Lemma 3.11(i),
$\pi _2$
. So by Lemma 3.11(i),
![]() $I"$
coincides with
$I"$
coincides with
![]() $I'$
. This implies that
$I'$
. This implies that
![]() $\bar Z^{\prime }_0=\pi _1(I')$
; hence,
$\bar Z^{\prime }_0=\pi _1(I')$
; hence,
![]() $S_0\in \bar Z^{\prime }_0$
and therefore, the general surface
$S_0\in \bar Z^{\prime }_0$
and therefore, the general surface
![]() $S^{\prime }_0\in \bar Z^{\prime }_0$
has a unique
$S^{\prime }_0\in \bar Z^{\prime }_0$
has a unique
![]() $T_1$
singularity. By Lemma 3.2, the assertion (ii) follows.
$T_1$
singularity. By Lemma 3.2, the assertion (ii) follows.
To prove (iii), we remark first of all that (ii) implies that
![]() $\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
is nonempty and there is an irreducible component
$\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
is nonempty and there is an irreducible component
![]() $\mathcal V$
of
$\mathcal V$
of
![]() $\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
that dominates
$\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
that dominates
![]() $\mathbb {D}$
and contains
$\mathbb {D}$
and contains
![]() $[S_0]$
. The general point in
$[S_0]$
. The general point in
![]() $\mathcal V$
corresponds to a surface
$\mathcal V$
corresponds to a surface
![]() $S_t$
with
$S_t$
with
![]() $t\neq 0$
, with a unique node at a general point
$t\neq 0$
, with a unique node at a general point
![]() $p_t\in \mathcal {X}_t$
. Moreover, since
$p_t\in \mathcal {X}_t$
. Moreover, since
![]() $[S_0]$
is a smooth point of
$[S_0]$
is a smooth point of
![]() $\mathcal H$
, we have that
$\mathcal H$
, we have that
![]() $[S_t]$
is a smooth point of
$[S_t]$
is a smooth point of
![]() $\mathcal H$
, and by the hypothesis (c) and by semicontinuity, we have that
$\mathcal H$
, and by the hypothesis (c) and by semicontinuity, we have that
![]() $h^1(S_t, \mathcal N_{S_t|\mathcal {X}_t}\otimes I_{p_t})=0$
. This yields that
$h^1(S_t, \mathcal N_{S_t|\mathcal {X}_t}\otimes I_{p_t})=0$
. This yields that
![]() $\mathcal V\cap \mathcal H_t$
is smooth of dimension
$\mathcal V\cap \mathcal H_t$
is smooth of dimension
![]() $\dim (\mathcal H_t)-1$
. Hence,
$\dim (\mathcal H_t)-1$
. Hence,
![]() $\mathcal V$
has dimension
$\mathcal V$
has dimension
![]() $\dim (\mathcal H)-1$
. To prove that
$\dim (\mathcal H)-1$
. To prove that
![]() $\mathcal V$
is reduced, it suffices to prove that
$\mathcal V$
is reduced, it suffices to prove that
![]() $\mathcal V$
is smooth at
$\mathcal V$
is smooth at
![]() $[S_t]$
. To see this, consider the exact sequence
$[S_t]$
. To see this, consider the exact sequence
where
![]() $T^1_{S_t}$
is supported on
$T^1_{S_t}$
is supported on
![]() $p_t$
with stalk
$p_t$
with stalk
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $H^0(S_t, \mathcal N^{\prime }_{S_t|\mathcal {X}})$
is the Zariski tangent space to
$H^0(S_t, \mathcal N^{\prime }_{S_t|\mathcal {X}})$
is the Zariski tangent space to
![]() $\mathcal V$
at
$\mathcal V$
at
![]() $[S_t]$
. The map
$[S_t]$
. The map
is surjective because
![]() $S_t$
is smoothable inside
$S_t$
is smoothable inside
![]() $\mathcal H$
, by the hypothesis (2) at the beginning of this section. Hence,
$\mathcal H$
, by the hypothesis (2) at the beginning of this section. Hence,
![]() $h^0(S_t, \mathcal N^{\prime }_{S_t|\mathcal {X}})=h^0(S_t, \mathcal N_{S_t|\mathcal {X}})-1=\dim (\mathcal H)-1$
, as wanted.
$h^0(S_t, \mathcal N^{\prime }_{S_t|\mathcal {X}})=h^0(S_t, \mathcal N_{S_t|\mathcal {X}})-1=\dim (\mathcal H)-1$
, as wanted.
We can now prove the main result of this section extending Proposition 3.10 to the case
![]() $\delta>1$
:
$\delta>1$
:
Theorem 3.13. Set up as in Proposition 3.10. In particular, we have the following condition: the subspace of sections of
![]() $H^0(\mathcal {X}_0,\mathcal L_0)$
that vanish on
$H^0(\mathcal {X}_0,\mathcal L_0)$
that vanish on
![]() $R=A\cap B$
, with A and B the irreducible components of
$R=A\cap B$
, with A and B the irreducible components of
![]() $\mathcal {X}_0$
, has codimension strictly larger than 1 in
$\mathcal {X}_0$
, has codimension strictly larger than 1 in
![]() $H^0(\mathcal {X}_0,\mathcal L_0)$
.
$H^0(\mathcal {X}_0,\mathcal L_0)$
.
Let
![]() $S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a surface corresponding to a section of
$S_0=S_A\cup S_B\subset \mathcal {X}_0$
be a surface corresponding to a section of
![]() $\mathcal L_0$
. We suppose that:
$\mathcal L_0$
. We suppose that:
-
(a)
 $S_A$
and
$S_A$
and
 $S_B$
have, respectively,
$S_B$
have, respectively,
 $\delta _A$
and
$\delta _A$
and
 $\delta _B$
nodes
$\delta _B$
nodes
 $p_{A,1},\ldots , p_{A,\delta _A}$
and
$p_{A,1},\ldots , p_{A,\delta _A}$
and
 $p_{B,1},\ldots , p_{B,\delta _B}$
off R are elsewhere smooth and intersect transversally along a curve
$p_{B,1},\ldots , p_{B,\delta _B}$
off R are elsewhere smooth and intersect transversally along a curve
 $C=S_A\cap S_B$
, except for
$C=S_A\cap S_B$
, except for
 $\delta _R$
distinct points
$\delta _R$
distinct points
 $p_{R,1}, \ldots , p_{R,\delta _R} \in C\subset R$
, where
$p_{R,1}, \ldots , p_{R,\delta _R} \in C\subset R$
, where
 $S_0$
has singularities of type
$S_0$
has singularities of type
 $T_1$
and that the hypotheses of Lemma 3.4 hold;
$T_1$
and that the hypotheses of Lemma 3.4 hold; -
(b) the sublinear system
 $\mathcal L_0(2,p_i)$
of
$\mathcal L_0(2,p_i)$
of
 $|\mathcal L_0|$
of surfaces with at least a
$|\mathcal L_0|$
of surfaces with at least a
 $T_1$
singularity at
$T_1$
singularity at
 $p_i$
has codimension 3 in
$p_i$
has codimension 3 in
 $|\mathcal L_0|$
, for every
$|\mathcal L_0|$
, for every
 $1\leqslant i\leqslant \delta $
;
$1\leqslant i\leqslant \delta $
; -
(c) if
 $\mathfrak Z$
is the
$\mathfrak Z$
is the
 $0$
-dimensional scheme of length
$0$
-dimensional scheme of length
 $\delta =\delta _A+\delta _B+\delta _R$
given by then
$\delta =\delta _A+\delta _B+\delta _R$
given by then $$ \begin{align*}\mathfrak Z= \sum_{i=1}^{\delta_A} p_{A,i}+\sum_{i=1}^{\delta_B} p_{B,i}+\sum_{i=1}^{\delta_R} p_{R,i}, \end{align*} $$
$$ \begin{align*}\mathfrak Z= \sum_{i=1}^{\delta_A} p_{A,i}+\sum_{i=1}^{\delta_B} p_{B,i}+\sum_{i=1}^{\delta_R} p_{R,i}, \end{align*} $$
 $H^1(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\mathfrak Z|\mathcal {X}_0})=0$
(where
$H^1(S_0, \mathcal N_{S_0|\mathcal {X}_0}\otimes I_{\mathfrak Z|\mathcal {X}_0})=0$
(where
 $I_{\mathfrak Z|\mathcal {X}_0}$
is the ideal sheaf of the scheme
$I_{\mathfrak Z|\mathcal {X}_0}$
is the ideal sheaf of the scheme
 $\mathfrak Z$
in
$\mathfrak Z$
in
 $\mathcal {X}_0$
).
$\mathcal {X}_0$
).
Then:
-
(i) S can be deformed to a
 $\delta $
-nodal surface
$\delta $
-nodal surface
 $S_t\subset \mathcal {X}_t$
;
$S_t\subset \mathcal {X}_t$
; -
(ii) if
 $\mathbb {T}\subseteq \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
is the unique irreducible component containing
$\mathbb {T}\subseteq \mathbb {T}_{\delta _A,\delta _B,\delta _R}$
is the unique irreducible component containing
 $[S]$
, then there exists an irreducible component
$[S]$
, then there exists an irreducible component
 $\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_\delta $
of dimension
$\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_\delta $
of dimension
 $\dim (\mathcal H)-\delta $
whose central fibre
$\dim (\mathcal H)-\delta $
whose central fibre
 $\mathcal V_0$
contains
$\mathcal V_0$
contains
 $\mathbb {T}$
as an irreducible component.
$\mathbb {T}$
as an irreducible component.
Proof. Again, by Corollary 3.8.1,
![]() $[S_0]$
is a smooth point for
$[S_0]$
is a smooth point for
![]() $\mathcal H^{\mathcal {X}|\mathbb {D}}$
. Moreover, by Corollary 3.8.3,
$\mathcal H^{\mathcal {X}|\mathbb {D}}$
. Moreover, by Corollary 3.8.3,
![]() $\mathbb {T}_{\delta _A,\delta _B,\delta _R}$
is smooth at
$\mathbb {T}_{\delta _A,\delta _B,\delta _R}$
is smooth at
![]() $[S_0]$
.
$[S_0]$
.
We denote by
![]() $\mathbb {T}$
the unique irreducible component of
$\mathbb {T}$
the unique irreducible component of
![]() $\mathbb {T}_{\delta _A,\delta _B,\delta _R}$
containing
$\mathbb {T}_{\delta _A,\delta _B,\delta _R}$
containing
![]() $[S_0]$
, which is smooth at
$[S_0]$
, which is smooth at
![]() $[S_0]$
. Furthermore, we set
$[S_0]$
. Furthermore, we set
![]() $\mathfrak Z=\mathfrak Z_{A}+\mathfrak Z_{B}+\mathfrak Z_{R}$
, where
$\mathfrak Z=\mathfrak Z_{A}+\mathfrak Z_{B}+\mathfrak Z_{R}$
, where
![]() $\mathfrak Z_A$
is the scheme of nodes of
$\mathfrak Z_A$
is the scheme of nodes of
![]() $S_0$
on
$S_0$
on
![]() $A$
,
$A$
,
![]() $\mathfrak Z_B$
is the scheme of nodes of
$\mathfrak Z_B$
is the scheme of nodes of
![]() $S_0$
on
$S_0$
on
![]() $B$
, and
$B$
, and
![]() $\mathfrak Z_R$
is the scheme of
$\mathfrak Z_R$
is the scheme of
![]() $T_1$
-singularities of
$T_1$
-singularities of
![]() $S_0$
.
$S_0$
.
Again by Corollary 3.8.3, in an analytic neighborhood of
![]() $[S]$
,
$[S]$
,
![]() $\mathbb {T}$
consists of an analytic branch
$\mathbb {T}$
consists of an analytic branch
![]() $\mathcal T$
that is the transverse intersection of
$\mathcal T$
that is the transverse intersection of
![]() $\delta $
smooth analytic branches of dimension
$\delta $
smooth analytic branches of dimension
![]() $h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-1$
, each branch corresponding to the locus of deformations of
$h^0(S_0, \mathcal N_{S_0|\mathcal {X}_0})-1$
, each branch corresponding to the locus of deformations of
![]() $S_0$
that are equisingular at a given point in
$S_0$
that are equisingular at a given point in
![]() $\mathfrak Z$
; that is, we have that
$\mathfrak Z$
; that is, we have that
The general element
![]() $S^{\prime }_0$
of
$S^{\prime }_0$
of
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is a surface in
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is a surface in
![]() $\mathcal {X}_0$
that has a unique singularity analytically equivalent to the singularity of
$\mathcal {X}_0$
that has a unique singularity analytically equivalent to the singularity of
![]() $S_0$
at p (i.e., a node if
$S_0$
at p (i.e., a node if
![]() $p\in \mathfrak Z_A+\mathfrak Z_B$
, a
$p\in \mathfrak Z_A+\mathfrak Z_B$
, a
![]() $T_1$
singularity otherwise).
$T_1$
singularity otherwise).
By Proposition 3.9, for every
![]() $p\in \mathfrak Z_A+\mathfrak Z_B$
,
$p\in \mathfrak Z_A+\mathfrak Z_B$
,
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is contained in
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is contained in
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}}$
as a subvariety of codimension 1, and
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}}$
as a subvariety of codimension 1, and
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}}$
is an analytic branch of the Severi variety
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}}$
is an analytic branch of the Severi variety
![]() $\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
.
$\mathcal V^{\mathcal {X}|\mathbb {D}}_1$
.
If
![]() $p\in \mathfrak Z_R$
, then by the hypothesis (b), for general element
$p\in \mathfrak Z_R$
, then by the hypothesis (b), for general element
![]() $S^{\prime }_0$
of
$S^{\prime }_0$
of
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
, the condition (b) of Proposition 3.10 holds. Then, by Proposition 3.10,
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
, the condition (b) of Proposition 3.10 holds. Then, by Proposition 3.10,
![]() $\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is contained, as a subvariety of codimension 1, in an analytic branch
$\mathcal {ES}_{[S_0],p}^{\mathcal {X}_0}$
is contained, as a subvariety of codimension 1, in an analytic branch
![]() $\mathcal T_p$
of
$\mathcal T_p$
of
![]() $\mathcal V_1^{\mathcal {X}|\mathbb {D}}$
having codimension
$\mathcal V_1^{\mathcal {X}|\mathbb {D}}$
having codimension
![]() $1$
in
$1$
in
![]() $\mathcal H$
, which is smooth at the general point corresponding to a
$\mathcal H$
, which is smooth at the general point corresponding to a
![]() $1$
-nodal surface.
$1$
-nodal surface.
Now, the intersection
has codimension at most
![]() $\delta $
in
$\delta $
in
![]() $\mathcal H$
, and it contains the smooth analytic branch
$\mathcal H$
, and it contains the smooth analytic branch
![]() $\mathcal T$
of
$\mathcal T$
of
![]() $\mathbb {T}$
, which has codimension
$\mathbb {T}$
, which has codimension
![]() $\delta +1$
in
$\delta +1$
in
![]() $\mathcal H$
. The general element of
$\mathcal H$
. The general element of
![]() $ \mathcal T' $
corresponds to a surface
$ \mathcal T' $
corresponds to a surface
![]() $\tilde S$
, not contained in
$\tilde S$
, not contained in
![]() $\mathcal {X}_0$
, with at least
$\mathcal {X}_0$
, with at least
![]() $\delta $
singularities, precisely
$\delta $
singularities, precisely
![]() $\delta _A$
(resp.
$\delta _A$
(resp.
![]() $\delta _B$
) singularities in neighborhoods of the nodes
$\delta _B$
) singularities in neighborhoods of the nodes
![]() $p\in \mathfrak Z_A$
(resp.
$p\in \mathfrak Z_A$
(resp.
![]() $p\in \mathfrak Z_B$
) and
$p\in \mathfrak Z_B$
) and
![]() $\delta _R$
singularities in neighborhoods of the
$\delta _R$
singularities in neighborhoods of the
![]() $T_1$
singularities
$T_1$
singularities
![]() $p\in \mathfrak Z_R$
. Taking into account Lemma 3.2, we deduce that
$p\in \mathfrak Z_R$
. Taking into account Lemma 3.2, we deduce that
![]() $\tilde S$
has
$\tilde S$
has
![]() $\delta $
nodes and no further singularities. This proves (i).
$\delta $
nodes and no further singularities. This proves (i).
If
![]() $ \tilde S\subset \mathcal {X}_t$
and it has nodes at
$ \tilde S\subset \mathcal {X}_t$
and it has nodes at
![]() $\tilde q_1,...,\tilde q_\delta $
, by semicontinuity, we have that
$\tilde q_1,...,\tilde q_\delta $
, by semicontinuity, we have that
![]() $H^0(\tilde S,\mathcal N_{\tilde S|\mathcal {X}_t}\otimes I_{\{\tilde q_1,...,\tilde q_\delta \}|\mathcal {X}_t})$
has dimension
$H^0(\tilde S,\mathcal N_{\tilde S|\mathcal {X}_t}\otimes I_{\{\tilde q_1,...,\tilde q_\delta \}|\mathcal {X}_t})$
has dimension
![]() $\dim (\mathcal H_t)-\delta $
. Thus,
$\dim (\mathcal H_t)-\delta $
. Thus,
![]() $ \mathcal T' $
is an analytic branch containing the point
$ \mathcal T' $
is an analytic branch containing the point
![]() $[\tilde S]$
in an irreducible component
$[\tilde S]$
in an irreducible component
![]() $\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_\delta $
of dimension
$\mathcal V\subset \mathcal V^{\mathcal {X}|\mathbb {D}}_\delta $
of dimension
![]() $\dim (\mathcal H)-\delta $
whose central fibre
$\dim (\mathcal H)-\delta $
whose central fibre
![]() $\mathcal V_0$
contains
$\mathcal V_0$
contains
![]() $\mathbb {T}$
as an irreducible component. This proves (ii).
$\mathbb {T}$
as an irreducible component. This proves (ii).
4. Applications
4.1. Severi varieties
Let X be a smooth irreducible projective complex threefold. Let L be a line bundle on X such that the general surface in the linear system
![]() $| L|$
is smooth and irreducible. We denote by
$| L|$
is smooth and irreducible. We denote by
![]() $V^{X, |L|}_\delta $
the Severi variety, that is the locally closed subscheme in
$V^{X, |L|}_\delta $
the Severi variety, that is the locally closed subscheme in
![]() $|L|$
parametrizing surfaces S in
$|L|$
parametrizing surfaces S in
![]() $|L|$
which are reduced and with only
$|L|$
which are reduced and with only
![]() $\delta $
nodes as singularities. If
$\delta $
nodes as singularities. If
![]() $[S]\in V^{X, |L|}_\delta $
, then the Zariski tangent space to
$[S]\in V^{X, |L|}_\delta $
, then the Zariski tangent space to
![]() $V^{X, |L|}_\delta $
at
$V^{X, |L|}_\delta $
at
![]() $[S]$
coincides with
$[S]$
coincides with
where N is the reduced scheme of nodes of S. In particular,
![]() $ \dim (V^{X, |L|}_\delta )\leqslant h^0(S, \mathcal {O}_S(L)\otimes I_{N|S}). $
Moreover, by standard deformation theory,
$ \dim (V^{X, |L|}_\delta )\leqslant h^0(S, \mathcal {O}_S(L)\otimes I_{N|S}). $
Moreover, by standard deformation theory,
![]() $H^1(S, \mathcal {O}_S(L)\otimes I_{N|S})$
is an obstruction space for
$H^1(S, \mathcal {O}_S(L)\otimes I_{N|S})$
is an obstruction space for
![]() $\mathcal {O}_ {V^{X, |L|}_\delta ,[S]},$
and thus,
$\mathcal {O}_ {V^{X, |L|}_\delta ,[S]},$
and thus,
If
![]() $h^1(S, \mathcal {O}_S(L)\otimes I_{N|S})=0$
, then
$h^1(S, \mathcal {O}_S(L)\otimes I_{N|S})=0$
, then
![]() $V^{X, |L|}_\delta $
is smooth at
$V^{X, |L|}_\delta $
is smooth at
![]() $[S]$
of dimension
$[S]$
of dimension
In this case, one says that
![]() $[S]$
is a regular point of the
$[S]$
is a regular point of the
![]() $\dim (V^{X, |L|}_\delta )$
. An irreducible component V of
$\dim (V^{X, |L|}_\delta )$
. An irreducible component V of
![]() $\dim (V^{X, |L|}_\delta )$
is said to be regular if it is regular at its general point.
$\dim (V^{X, |L|}_\delta )$
is said to be regular if it is regular at its general point.
Remark 4.1. Suppose V is a regular irreducible component of
![]() $\dim (V^{X, |L|}_\delta )$
. By standard deformation theory already used in Section 3, the nodes of the surface corresponding to any smooth point in V can be independently smoothed. This implies that there are regular components of
$\dim (V^{X, |L|}_\delta )$
. By standard deformation theory already used in Section 3, the nodes of the surface corresponding to any smooth point in V can be independently smoothed. This implies that there are regular components of
![]() $\dim (V^{X, |L|}_{\delta '})$
for any
$\dim (V^{X, |L|}_{\delta '})$
for any
![]() $\delta '<\delta $
.
$\delta '<\delta $
.
One can consider the following two questions.
Problem 4.2. Given X and L as above, which is the maximal value of
![]() $\delta $
such that the Severi variety
$\delta $
such that the Severi variety
![]() $V^{X, |L|}_\delta $
is nonempty?
$V^{X, |L|}_\delta $
is nonempty?
Problem 4.3. Given X and L as above, which is the maximal value of
![]() $\delta $
such that the Severi variety
$\delta $
such that the Severi variety
![]() $V^{X, |L|}_\delta $
has a regular component?
$V^{X, |L|}_\delta $
has a regular component?
As for Problem 4.2, this is a classical and difficult question, for which there are several contributions, too many to be quoted here. Probably the most efficient one is given by the Miyaoka’s bound [Reference Miyaoka15, Formulae (2) and (8)]. In particular, the problem has been completely solved for
![]() $X=\mathbb {P}^3$
and
$X=\mathbb {P}^3$
and
![]() $L=\mathcal {O}_{\mathbb {P}^3}(d)$
with
$L=\mathcal {O}_{\mathbb {P}^3}(d)$
with
![]() $d\leqslant 6$
(see, for example, [Reference Labs14] and references therein). However, in this section, we will not consider Problem 4.2, but we will give some contribution to Problem 4.3.
$d\leqslant 6$
(see, for example, [Reference Labs14] and references therein). However, in this section, we will not consider Problem 4.2, but we will give some contribution to Problem 4.3.
Remark 4.4. One could be tempted to believe that the maximal
![]() $\delta $
for which the Severi variety is nonempty is bounded above by the dimension of
$\delta $
for which the Severi variety is nonempty is bounded above by the dimension of
![]() $|L|$
. This is not true. In fact, there are classical examples, for
$|L|$
. This is not true. In fact, there are classical examples, for
![]() $X=\mathbb {P}^3$
and
$X=\mathbb {P}^3$
and
![]() $L=\mathcal {O}_{\mathbb {P}^3}(d)$
for suitable d, for which
$L=\mathcal {O}_{\mathbb {P}^3}(d)$
for suitable d, for which
![]() $V^{X, |L|}_\delta $
is nonempty and
$V^{X, |L|}_\delta $
is nonempty and
![]() $\delta $
is greater than the dimension of
$\delta $
is greater than the dimension of
![]() $|L|$
(cf. [Reference Beauville1], [Reference Segre19]). In these cases, every component of the Severi variety is not regular.
$|L|$
(cf. [Reference Beauville1], [Reference Segre19]). In these cases, every component of the Severi variety is not regular.
Remark 4.5. Referring to Problem 4.3, it is rather natural to conjecture that the
![]() $\delta $
which answers the question should be bounded below by
$\delta $
which answers the question should be bounded below by
![]() $\delta _0=[{\dim (|L|)\over 4 }]$
. The reason for such a conjecture is the following: choose
$\delta _0=[{\dim (|L|)\over 4 }]$
. The reason for such a conjecture is the following: choose
![]() $p_1,\ldots ,p_{\delta _0}$
general points on X. Since a double point imposes at most four conditions to
$p_1,\ldots ,p_{\delta _0}$
general points on X. Since a double point imposes at most four conditions to
![]() $|L|$
, certainly there are surfaces which are singular at every
$|L|$
, certainly there are surfaces which are singular at every
![]() $p_i$
. If the general such surface has only nodes at
$p_i$
. If the general such surface has only nodes at
![]() $p_1,\ldots ,p_{\delta _0}$
and no other singularities, then it belongs to a regular component of the Severi variety. However, this heuristic argument is very difficult to be made rigorous in general.
$p_1,\ldots ,p_{\delta _0}$
and no other singularities, then it belongs to a regular component of the Severi variety. However, this heuristic argument is very difficult to be made rigorous in general.
4.2. The case of
 $\mathbb {P}^3$
$\mathbb {P}^3$
In this section, we give a contribution to Problem 4.3, in the case
![]() $X=\mathbb {P}^3$
and
$X=\mathbb {P}^3$
and
![]() $L=\mathcal {O}_{\mathbb {P}^3}(d)$
. More precisely, we will prove the following:
$L=\mathcal {O}_{\mathbb {P}^3}(d)$
. More precisely, we will prove the following:
Theorem 4.6. There is an irreducible, regular component of
![]() $V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_{\delta }$
, for any
$V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_{\delta }$
, for any
![]() $\delta \leqslant {{d-1}\choose 2}$
.
$\delta \leqslant {{d-1}\choose 2}$
.
Proof. In view of Remark 4.1, it is sufficent to consider only the case
![]() $\delta ={{d-1}\choose 2}.$
$\delta ={{d-1}\choose 2}.$
Let
![]() $\mathcal {X}'=\mathbb {P}^3\times \mathbb {D}\to \mathbb {D}$
be a trivial family. Let us consider
$\mathcal {X}'=\mathbb {P}^3\times \mathbb {D}\to \mathbb {D}$
be a trivial family. Let us consider
![]() $\mathcal {X}\to \mathcal {X}'$
the blow-up of a point q in the central fibre
$\mathcal {X}\to \mathcal {X}'$
the blow-up of a point q in the central fibre
![]() $\mathbb {P}^3$
over
$\mathbb {P}^3$
over
![]() $0\in \mathbb {D}$
. Let
$0\in \mathbb {D}$
. Let
![]() $\mathcal {X}\to \mathbb {D}$
be the new family. The fibre over
$\mathcal {X}\to \mathbb {D}$
be the new family. The fibre over
![]() $t\in \mathbb {D}\setminus \{0\}$
of this family is
$t\in \mathbb {D}\setminus \{0\}$
of this family is
![]() $\mathcal {X}_t\cong \mathbb {P}^3$
. The central fibre
$\mathcal {X}_t\cong \mathbb {P}^3$
. The central fibre
![]() $\mathcal {X}_0$
consists of two components
$\mathcal {X}_0$
consists of two components
![]() $A\cup B$
, where
$A\cup B$
, where
![]() $f:A\to \mathbb {P}^3$
is the blow-up of
$f:A\to \mathbb {P}^3$
is the blow-up of
![]() $\mathbb {P}^3$
at q, whereas
$\mathbb {P}^3$
at q, whereas
![]() $B\cong \mathbb {P}^3$
is the exceptional divisor in
$B\cong \mathbb {P}^3$
is the exceptional divisor in
![]() $\mathcal {X}$
, and
$\mathcal {X}$
, and
![]() $A\cap B=R\cong \mathbb {P}^2$
is the exceptional divisor in A and a plane in B.
$A\cap B=R\cong \mathbb {P}^2$
is the exceptional divisor in A and a plane in B.
On
![]() $\mathcal {X}'$
, there is a line bundle
$\mathcal {X}'$
, there is a line bundle
![]() $\mathcal L'$
, which is the pull-back via the first projection, of
$\mathcal L'$
, which is the pull-back via the first projection, of
![]() $\mathcal {O}_{\mathbb {P}^3}(d)$
. We pull this back to
$\mathcal {O}_{\mathbb {P}^3}(d)$
. We pull this back to
![]() $\mathcal {X}$
and denote it
$\mathcal {X}$
and denote it
![]() $\mathcal L$
. Now we consider on
$\mathcal L$
. Now we consider on
![]() $\mathcal {X}$
the line bundle
$\mathcal {X}$
the line bundle
![]() $\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
. Its restriction to the general fibre
$\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
. Its restriction to the general fibre
![]() $\mathcal {X}_t$
is given by
$\mathcal {X}_t$
is given by
![]() $(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_{\mathcal {X}_t}\simeq \mathcal {O}_{\mathbb {P}^3}(d)$
. As for the restriction of
$(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_{\mathcal {X}_t}\simeq \mathcal {O}_{\mathbb {P}^3}(d)$
. As for the restriction of
![]() $\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
to
$\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
to
![]() $\mathcal {X}_0$
, we observe that
$\mathcal {X}_0$
, we observe that
![]() $(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_A\simeq \mathcal {O}_A(d)\otimes \mathcal {O}_A(-(d-1)R)$
, where
$(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_A\simeq \mathcal {O}_A(d)\otimes \mathcal {O}_A(-(d-1)R)$
, where
![]() $\mathcal {O}_A(d)\simeq f^{*}(\mathcal {O}_{\mathbb {P}^3}(d))$
, whereas
$\mathcal {O}_A(d)\simeq f^{*}(\mathcal {O}_{\mathbb {P}^3}(d))$
, whereas
![]() $(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_B\simeq \mathcal {O}_{\mathbb {P}^3}(d-1)$
and, finally, the restriction of
$(\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B))|_B\simeq \mathcal {O}_{\mathbb {P}^3}(d-1)$
and, finally, the restriction of
![]() $\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
to R is
$\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
to R is
![]() $\mathcal {O}_{\mathbb {P}^2}(d-1)$
. One easily checks that the line bundle
$\mathcal {O}_{\mathbb {P}^2}(d-1)$
. One easily checks that the line bundle
![]() $\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
verifies the hypotheses (1), (2) and (3) at the beginning of Section 3.2.3.
$\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)$
verifies the hypotheses (1), (2) and (3) at the beginning of Section 3.2.3.
We now consider on R a curve C which consists of the union of
![]() $d-1$
general lines. It has
$d-1$
general lines. It has
![]() $\delta ={{d-1}\choose 2}$
nodes as singularities. By standard application of Bertini’s theorem, there exists a smooth surface
$\delta ={{d-1}\choose 2}$
nodes as singularities. By standard application of Bertini’s theorem, there exists a smooth surface
![]() $S_B$
in B of degree
$S_B$
in B of degree
![]() $d-1$
cutting out on R the curve C. Similarly, there exists a smooth surface
$d-1$
cutting out on R the curve C. Similarly, there exists a smooth surface
![]() $S_A\in |\mathcal {O}_A(d)\otimes \mathcal {O}_A(-(d-1)R)|$
restricting to C on R. To see this, let
$S_A\in |\mathcal {O}_A(d)\otimes \mathcal {O}_A(-(d-1)R)|$
restricting to C on R. To see this, let
![]() $(x,y,z)$
be an affine coordinates system on
$(x,y,z)$
be an affine coordinates system on
![]() $\mathbb {P}^3$
centered at q. If
$\mathbb {P}^3$
centered at q. If
![]() $\phi _1(x,y,z)=0$
is the equation of C in the plane at infinity, and
$\phi _1(x,y,z)=0$
is the equation of C in the plane at infinity, and
![]() $\phi _2(x,y,z)$
is a general homogeneous polynomial of degree d in
$\phi _2(x,y,z)$
is a general homogeneous polynomial of degree d in
![]() $(x,y,z)$
, then the projective closure
$(x,y,z)$
, then the projective closure
![]() $S_B$
of the degree d affine surface with equation
$S_B$
of the degree d affine surface with equation
![]() $\phi _1(x,y,z)+\phi _2(x,y,z)=0$
has a point of multiplicity
$\phi _1(x,y,z)+\phi _2(x,y,z)=0$
has a point of multiplicity
![]() $d-1$
at q and no other singularities, and its minimal resolution obtained by blowing up q is the required surface.
$d-1$
at q and no other singularities, and its minimal resolution obtained by blowing up q is the required surface.
Now
![]() $S_0=S_A\cup S_B$
is a Cartier divisor in
$S_0=S_A\cup S_B$
is a Cartier divisor in
![]() $\mathcal {X}_0$
belonging to the linear system
$\mathcal {X}_0$
belonging to the linear system
![]() $|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|$
. Moreover,
$|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|$
. Moreover,
![]() $S_0$
verifies all hypotheses of Theorem 3.13. In particular, if
$S_0$
verifies all hypotheses of Theorem 3.13. In particular, if
![]() $\mathfrak Z$
is the reduced scheme of the nodes of C, then
$\mathfrak Z$
is the reduced scheme of the nodes of C, then
![]() $\mathfrak Z$
imposes independent conditions to
$\mathfrak Z$
imposes independent conditions to
![]() $|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|_R|=|\mathcal {O}_{\mathbb {P}^2}(d-1)|$
, and therefore to
$|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|_R|=|\mathcal {O}_{\mathbb {P}^2}(d-1)|$
, and therefore to
![]() $|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|$
, because the Severi varieties of nodal curves in the plane are well known to be regular. By applying Theorem 3.13, one may deform
$|\mathcal L\otimes \mathcal {O}_{\mathcal {X}}((1-d)B)|$
, because the Severi varieties of nodal curves in the plane are well known to be regular. By applying Theorem 3.13, one may deform
![]() $S_0$
to a surface
$S_0$
to a surface
![]() $S_t\subset \mathcal {X}_t$
with
$S_t\subset \mathcal {X}_t$
with
![]() $\delta $
nodes and no further singularities, which are deformations of the
$\delta $
nodes and no further singularities, which are deformations of the
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
of
$T_1$
of
![]() $S_0$
. Finally, the nodes of
$S_0$
. Finally, the nodes of
![]() $S_t$
impose independent conditions to surfaces of degree d on
$S_t$
impose independent conditions to surfaces of degree d on
![]() $\mathcal {X}_t\simeq \mathbb {P}^3$
. Hence,
$\mathcal {X}_t\simeq \mathbb {P}^3$
. Hence,
![]() $[S_t]\in V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_{\delta }$
belongs to a regular component of the Severi variety.
$[S_t]\in V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_{\delta }$
belongs to a regular component of the Severi variety.
Remark 4.7. Taking into account Remark 4.5, we believe that the previous result is far from being sharp, not even asymptotically. Indeed, we may expect that the bound on
![]() $\delta $
for the existence of regular components of the Severi variety of nodal surfaces of degree d in
$\delta $
for the existence of regular components of the Severi variety of nodal surfaces of degree d in
![]() $\mathbb {P}^3$
could asymptotically go as
$\mathbb {P}^3$
could asymptotically go as
![]() $\delta \sim {d^3\over 24}$
. See also [Reference Labs14, Corollary 4.1] and related references for a very large upper bound of the number of nodes
$\delta \sim {d^3\over 24}$
. See also [Reference Labs14, Corollary 4.1] and related references for a very large upper bound of the number of nodes
![]() $\delta $
of a surface in
$\delta $
of a surface in
![]() $\mathbb {P}^3$
in a regular component of the Severi variety (if nonempty). Moreover, our results could in principle be improved by imposing to
$\mathbb {P}^3$
in a regular component of the Severi variety (if nonempty). Moreover, our results could in principle be improved by imposing to
![]() $S_0$
nodes off R, but we do not dwell on this here.
$S_0$
nodes off R, but we do not dwell on this here.
Remark 4.8. The known results about Problem 4.3 are very few. For example, in [Reference Kloosterman13], one proves that if
![]() $V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_\delta $
is nonempty, then every component of it is regular for
$V^{\mathbb {P}^3, |\mathcal {O}_{\mathbb {P}^3}(d)|}_\delta $
is nonempty, then every component of it is regular for
![]() $d\leqslant 7$
and for
$d\leqslant 7$
and for
![]() $d\geqslant 8$
and
$d\geqslant 8$
and
![]() $\delta \leqslant 4d-5$
, and this last bound is sharp (the case
$\delta \leqslant 4d-5$
, and this last bound is sharp (the case
![]() $d\leqslant 7$
was already proved in [Reference Dimca8]). Nonemptiness results for
$d\leqslant 7$
was already proved in [Reference Dimca8]). Nonemptiness results for
![]() $d\leqslant 7$
are also well known (see, for example, [Reference Labs14, p. 120]). In particular, our Theorem 4.6 is, at the best of our knowledge, new as soon as
$d\leqslant 7$
are also well known (see, for example, [Reference Labs14, p. 120]). In particular, our Theorem 4.6 is, at the best of our knowledge, new as soon as
![]() $d\geqslant 8$
.
$d\geqslant 8$
.
4.3. Complete intersections in
 $\mathbb {P}^4$
$\mathbb {P}^4$
In this section, we want to provide a partial answer to Problem 4.3 in the case of complete intersections in
![]() $\mathbb {P}^4$
.
$\mathbb {P}^4$
.
Let X be a general hypersurface of degree
![]() $h\geqslant 2$
in
$h\geqslant 2$
in
![]() $\mathbb {P}^4$
. We consider on X the linear system
$\mathbb {P}^4$
. We consider on X the linear system
![]() $|\mathcal {O}_X(d)|$
. Our aim is to construct regular components of
$|\mathcal {O}_X(d)|$
. Our aim is to construct regular components of
![]() $V^{X,|\mathcal {O}_X(d)|}_\delta $
with suitable
$V^{X,|\mathcal {O}_X(d)|}_\delta $
with suitable
![]() $\delta $
.
$\delta $
.
Theorem 4.9. Let
![]() $d\geqslant h-1$
be an integer. There are regular components of
$d\geqslant h-1$
be an integer. There are regular components of
![]() $V^{X,|\mathcal {O}_X(d)|}_\delta $
for
$V^{X,|\mathcal {O}_X(d)|}_\delta $
for
 $$ \begin{align*}\delta\leqslant {{d+3}\choose 3}-{{d-h+1}\choose 3}-1.\end{align*} $$
$$ \begin{align*}\delta\leqslant {{d+3}\choose 3}-{{d-h+1}\choose 3}-1.\end{align*} $$
Proof. As usual, to prove the theorem, it suffices to do the case
 $$ \begin{align*}\delta={{d+3}\choose 3}-{{d-h+1}\choose 3}-1.\end{align*} $$
$$ \begin{align*}\delta={{d+3}\choose 3}-{{d-h+1}\choose 3}-1.\end{align*} $$
Let Y be a general hypersurface of
![]() $\mathbb {P}^4$
of degree
$\mathbb {P}^4$
of degree
![]() $h-1$
and H be a general hyperplane, cutting Y along a surface R, which is a general surface of degree
$h-1$
and H be a general hyperplane, cutting Y along a surface R, which is a general surface of degree
![]() $h-1$
in
$h-1$
in
![]() $H\simeq \mathbb {P}^3$
. Let X be a general hypersurface of degree h and let us consider the pencil generated by X and
$H\simeq \mathbb {P}^3$
. Let X be a general hypersurface of degree h and let us consider the pencil generated by X and
![]() $Y\cup H$
. Specifically, if X has equation
$Y\cup H$
. Specifically, if X has equation
![]() $f=0$
, Y has equation
$f=0$
, Y has equation
![]() $g=0$
and H has equation
$g=0$
and H has equation
![]() $\ell =0$
, we will consider the hypersurface
$\ell =0$
, we will consider the hypersurface
![]() $\mathcal {X}"$
in
$\mathcal {X}"$
in
![]() $\mathbb {P}^4\times \mathbb {A}^1 $
, with equation
$\mathbb {P}^4\times \mathbb {A}^1 $
, with equation
![]() $\{tf+g\ell =0,\,\mathrm {{with}}\,t\in \mathbb {A}^1\}$
. Via the second projection
$\{tf+g\ell =0,\,\mathrm {{with}}\,t\in \mathbb {A}^1\}$
. Via the second projection
![]() $\mathcal {X}"\to \mathbb {A}^1$
, this becomes a flat family of
$\mathcal {X}"\to \mathbb {A}^1$
, this becomes a flat family of
![]() $3$
-folds, with smooth general fibre
$3$
-folds, with smooth general fibre
![]() $\mathcal {X}^{\prime \prime }_t$
, corresponding to a general hypersurface of degree h in
$\mathcal {X}^{\prime \prime }_t$
, corresponding to a general hypersurface of degree h in
![]() $\mathbb {P}^4$
, and whose fibre over
$\mathbb {P}^4$
, and whose fibre over
![]() $0$
is
$0$
is
![]() $\mathcal {X}^{\prime \prime }_0=Y\cup H\subset \mathbb {P}^4$
. We are interested in the singularities of
$\mathcal {X}^{\prime \prime }_0=Y\cup H\subset \mathbb {P}^4$
. We are interested in the singularities of
![]() $\mathcal {X}"$
in a neighborhood of the central fibre (i.e., we are interested in what happens if t belongs to a disc
$\mathcal {X}"$
in a neighborhood of the central fibre (i.e., we are interested in what happens if t belongs to a disc
![]() $\mathbb {D}$
, centered at the origin). Thus, we consider the family
$\mathbb {D}$
, centered at the origin). Thus, we consider the family
It is immediate to see that the singular locus of
![]() $\mathcal {X}'$
coincides with the curve
$\mathcal {X}'$
coincides with the curve
![]() $D:t=f=g=\ell =0\subset \mathcal {X}^{\prime }_0$
, which is isomorphic to a smooth complete intersection curve of type
$D:t=f=g=\ell =0\subset \mathcal {X}^{\prime }_0$
, which is isomorphic to a smooth complete intersection curve of type
![]() $(1,h-1,h)$
in
$(1,h-1,h)$
in
![]() $\mathbb {P}^4$
cut out on
$\mathbb {P}^4$
cut out on
![]() $R=Y\cap H$
by X. Moreover,
$R=Y\cap H$
by X. Moreover,
![]() $\mathcal {X}'$
has double points along D with tangent cone a quadric of rank 4. We resolve these singularities by blowing up
$\mathcal {X}'$
has double points along D with tangent cone a quadric of rank 4. We resolve these singularities by blowing up
![]() $\mathcal {X}'$
along D. One obtains a new family
$\mathcal {X}'$
along D. One obtains a new family
![]() $\tilde {\mathcal {X}}\to \mathbb {D}$
with the same general fibre as
$\tilde {\mathcal {X}}\to \mathbb {D}$
with the same general fibre as
![]() $\mathcal {X}'\to \mathbb {D}$
and whose central fibre consists of three components
$\mathcal {X}'\to \mathbb {D}$
and whose central fibre consists of three components
![]() $\tilde Y$
and
$\tilde Y$
and
![]() $\tilde H$
, the blow-ups of Y and H along D and the exceptional divisor
$\tilde H$
, the blow-ups of Y and H along D and the exceptional divisor
![]() $\tilde {\Theta }$
that is a
$\tilde {\Theta }$
that is a
![]() $\mathbb {P}^1\times \mathbb {P}^1$
bundle over D. Now we can contract
$\mathbb {P}^1\times \mathbb {P}^1$
bundle over D. Now we can contract
![]() $ \tilde \Theta $
by contracting one of the two rulings of the
$ \tilde \Theta $
by contracting one of the two rulings of the
![]() $\mathbb {P}^1\times \mathbb {P}^1$
bundle. We choose to do this in the direction of Y. We obtain a new family of 3-folds
$\mathbb {P}^1\times \mathbb {P}^1$
bundle. We choose to do this in the direction of Y. We obtain a new family of 3-folds
![]() $\mathcal {X}\to \mathbb {D}$
, with
$\mathcal {X}\to \mathbb {D}$
, with
![]() $\mathcal {X}$
smooth, with fiber
$\mathcal {X}$
smooth, with fiber
![]() $\mathcal {X}_t=\mathcal {X}^{\prime }_t$
over
$\mathcal {X}_t=\mathcal {X}^{\prime }_t$
over
![]() $t\neq 0$
, and whose central fiber
$t\neq 0$
, and whose central fiber
![]() $\mathcal {X}_0=A\cup B$
, where now
$\mathcal {X}_0=A\cup B$
, where now
![]() $B=H\simeq \mathbb {P}^3$
and
$B=H\simeq \mathbb {P}^3$
and
![]() $A=\mathrm {Bl}_D(Y)$
is the blowing up of Y along D and A and B intersect transversally along a surface isomorphic to R, which we still denote by
$A=\mathrm {Bl}_D(Y)$
is the blowing up of Y along D and A and B intersect transversally along a surface isomorphic to R, which we still denote by
![]() $R=A\cap B$
. The exceptional divisor
$R=A\cap B$
. The exceptional divisor
![]() $\Theta $
in
$\Theta $
in
![]() $A=\mathrm { Bl}_D(Y)$
is a
$A=\mathrm { Bl}_D(Y)$
is a
![]() $\mathbb {P}^1$
-bundle on
$\mathbb {P}^1$
-bundle on
![]() $D\subset R$
, intersecting R along D. In particular,
$D\subset R$
, intersecting R along D. In particular,
![]() $\Theta \simeq \mathbb {P}(\mathcal N_{D|Y})$
.
$\Theta \simeq \mathbb {P}(\mathcal N_{D|Y})$
.
Notice that one has a natural morphism
![]() $\tilde {\mathcal {X}}\to \mathbb {P}^4$
. This factors through a morphism
$\tilde {\mathcal {X}}\to \mathbb {P}^4$
. This factors through a morphism
![]() $\phi : \mathcal {X}\to \mathbb {P}^4$
. The action of
$\phi : \mathcal {X}\to \mathbb {P}^4$
. The action of
![]() $\phi $
on
$\phi $
on
![]() $\mathcal {X}_0$
is as follows: it maps B isomorphically to H, and it maps A to Y by contracting the exceptional divisor
$\mathcal {X}_0$
is as follows: it maps B isomorphically to H, and it maps A to Y by contracting the exceptional divisor
![]() $\Theta $
. Let us now set
$\Theta $
. Let us now set
![]() $\mathcal L_d= \phi ^{*}(\mathcal {O}_{\mathbb {P}^4}(d))$
and assume that
$\mathcal L_d= \phi ^{*}(\mathcal {O}_{\mathbb {P}^4}(d))$
and assume that
![]() $d\geqslant h-1$
.
$d\geqslant h-1$
.
Recall that R is a general surface of degree
![]() $h-1$
in
$h-1$
in
![]() $\mathbb {P}^3$
, with
$\mathbb {P}^3$
, with
![]() $h\geqslant 2$
. By [Reference Chiantini and Ciliberto4],
$h\geqslant 2$
. By [Reference Chiantini and Ciliberto4],
![]() $V^{R, |\mathcal {O}_R(d)|}_\delta $
is nonempty and contains a regular component V for
$V^{R, |\mathcal {O}_R(d)|}_\delta $
is nonempty and contains a regular component V for
 $$ \begin{align*}\delta=\dim (|\mathcal{O}_R(d)|)={{d+3}\choose 3}-{{d-h+1}\choose 3}-1. \end{align*} $$
$$ \begin{align*}\delta=\dim (|\mathcal{O}_R(d)|)={{d+3}\choose 3}-{{d-h+1}\choose 3}-1. \end{align*} $$
So we can choose a general curve C in V, that is a complete intersection of type
![]() $(h-1,d)$
on R with
$(h-1,d)$
on R with
![]() $\delta $
nodes. Using Bertini’s theorem, we can assume that there is a divisor
$\delta $
nodes. Using Bertini’s theorem, we can assume that there is a divisor
![]() $S_0\in \mathcal L_{d|\mathcal {X}_0}$
that cuts out C on R and
$S_0\in \mathcal L_{d|\mathcal {X}_0}$
that cuts out C on R and
![]() $S_0=S_A\cup S_B$
(the notation is obvious), with
$S_0=S_A\cup S_B$
(the notation is obvious), with
![]() $S_A$
and
$S_A$
and
![]() $S_B$
smooth.
$S_B$
smooth.
Now
![]() $S_0$
verifies all hypotheses of Theorem 3.13. In particular, if
$S_0$
verifies all hypotheses of Theorem 3.13. In particular, if
![]() $\mathfrak Z$
is the reduced scheme of nodes of C, then
$\mathfrak Z$
is the reduced scheme of nodes of C, then
![]() $\mathfrak Z$
imposes independent conditions to
$\mathfrak Z$
imposes independent conditions to
![]() $\mathcal L_{d}|_{\mathcal {X}_0}$
because the component V of the Severi variety is regular. By applying Theorem 3.13, one may deform
$\mathcal L_{d}|_{\mathcal {X}_0}$
because the component V of the Severi variety is regular. By applying Theorem 3.13, one may deform
![]() $S_0$
to a surface
$S_0$
to a surface
![]() $S_t\subset \mathcal {X}_t$
with
$S_t\subset \mathcal {X}_t$
with
![]() $\delta $
nodes and no further singularities, which are deformations of the
$\delta $
nodes and no further singularities, which are deformations of the
![]() $\delta $
singularities of type
$\delta $
singularities of type
![]() $T_1$
of
$T_1$
of
![]() $S_0$
. Finally, the nodes of
$S_0$
. Finally, the nodes of
![]() $S_t$
impose independent conditions to surfaces in
$S_t$
impose independent conditions to surfaces in
![]() $|\mathcal {O}_{X_t}(d)|$
. Hence,
$|\mathcal {O}_{X_t}(d)|$
. Hence,
![]() $[S_t]\in V^{\mathcal {X}_t, |\mathcal {O}_{\mathcal {X}_t}(d)|}_{\delta }$
belongs to a regular component of the Severi variety, as wanted.
$[S_t]\in V^{\mathcal {X}_t, |\mathcal {O}_{\mathcal {X}_t}(d)|}_{\delta }$
belongs to a regular component of the Severi variety, as wanted.
Acknowledgements
The authors are grateful to the referee for careful reading. Moreover, the authors want to thank Th. Dedieu, B. Fantechi, R. Pardini and E. Sernesi for useful discussions on the topics of this paper.
Competing interest
The authors have no competing interests to declare.
Funding statement
The authors are members of GNSAGA of INdAM. In particular, the second author acknowledges funding from the GNSAGA of INdAM and the European Union - NextGenerationEU under the National Recovery and Resilience Plan (PNRR) - Mission 4 Education and research - Component 2 From research to business - Investment 1.1, Prin 2022 ‘Geometry of algebraic structures: moduli, invariants, deformations’, DD N. 104, 2/2/2022, proposal code 2022BTA242 - CUP J53D23003720006.