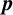 $\boldsymbol {p}$
-GROUPS
$\boldsymbol {p}$
-GROUPS
 $\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
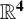 $\boldsymbol {{\mathbb {R}}^{4}}$
$\boldsymbol {{\mathbb {R}}^{4}}$