No CrossRef data available.
Published online by Cambridge University Press: 19 April 2022
We investigate some properties of complex structures on Lie algebras. In particular, we focus on nilpotent complex structures that are characterised by suitable J-invariant ascending or descending central series,
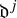 $\mathfrak {d}^{\,j}$
and
$\mathfrak {d}^{\,j}$
and
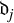 $\mathfrak {d}_j$
, respectively. We introduce a new descending series
$\mathfrak {d}_j$
, respectively. We introduce a new descending series
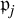 $\mathfrak {p}_j$
and use it to prove a new characterisation of nilpotent complex structures. We also examine whether nilpotent complex structures on stratified Lie algebras preserve the strata. We find that there exists a J-invariant stratification on a step
$\mathfrak {p}_j$
and use it to prove a new characterisation of nilpotent complex structures. We also examine whether nilpotent complex structures on stratified Lie algebras preserve the strata. We find that there exists a J-invariant stratification on a step
 $2$
nilpotent Lie algebra with a complex structure.
$2$
nilpotent Lie algebra with a complex structure.