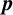 $\boldsymbol {p}$
-GROUPS
$\boldsymbol {p}$
-GROUPS
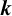 $\boldsymbol {k}$
-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$
-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
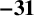 $\boldsymbol {-31}$
TO MODULAR FORMS
$\boldsymbol {-31}$
TO MODULAR FORMS