Arithmetic quasidensities are a large family of real-valued set functions partially defined on the power set of 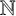 $\mathbb {N}$, including the asymptotic density, the Banach density and the analytic density. Let
$\mathbb {N}$, including the asymptotic density, the Banach density and the analytic density. Let 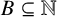 $B \subseteq \mathbb {N}$ be a nonempty set covering
$B \subseteq \mathbb {N}$ be a nonempty set covering 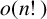 $o(n!)$ residue classes modulo
$o(n!)$ residue classes modulo 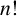 $n!$ as
$n!$ as 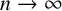 $n\to \infty $ (for example, the primes or the perfect powers). We show that, for each
$n\to \infty $ (for example, the primes or the perfect powers). We show that, for each 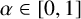 $\alpha \in [0,1]$, there is a set
$\alpha \in [0,1]$, there is a set 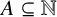 $A\subseteq \mathbb {N}$ such that, for every arithmetic quasidensity
$A\subseteq \mathbb {N}$ such that, for every arithmetic quasidensity 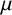 $\mu $, both A and the sumset
$\mu $, both A and the sumset 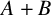 $A+B$ are in the domain of
$A+B$ are in the domain of 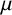 $\mu $ and, in addition,
$\mu $ and, in addition, 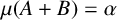 $\mu (A + B) = \alpha $. The proof relies on the properties of a little known density first considered by Buck [‘The measure theoretic approach to density’, Amer. J. Math. 68 (1946), 560–580].
$\mu (A + B) = \alpha $. The proof relies on the properties of a little known density first considered by Buck [‘The measure theoretic approach to density’, Amer. J. Math. 68 (1946), 560–580].
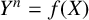 $Y^n=f(X)$ OVER FUNCTION FIELDS
$Y^n=f(X)$ OVER FUNCTION FIELDS
 $2$-COCYCLES OF FINITE GROUPS
$2$-COCYCLES OF FINITE GROUPS