The Cahn–Hilliard–Navier–Stokes (CHNS) partial differential equations (PDEs) provide a powerful framework for the study of the statistical mechanics and fluid dynamics of multiphase fluids. We provide an introduction to the equilibrium and non-equilibrium statistical mechanics of systems in which coexisting phases, distinguished from each other by scalar order parameters, are separated by an interface. We then introduce the coupled CHNS PDEs for two immiscible fluids and generalisations for (i) coexisting phases with different viscosities, (ii) CHNS with gravity, (iii) three-component fluids and (iv) the CHNS for active fluids. We discuss mathematical issues of the regularity of solutions of the CHNS PDEs. Finally we provide a survey of the rich variety of results that have been obtained by numerical studies of CHNS-type PDEs for diverse systems, including bubbles in turbulent flows, antibubbles, droplet and liquid-lens mergers, turbulence in the active-CHNS model and its generalisation that can lead to a self-propelled droplet.

In fluid dynamics, helicity measures the correlation between velocity and its curl, vorticity, over a spatial volume. Under ‘ideal’ conditions (vanishing viscosity and either homogeneneous density or when pressure may be regarded as a function of density alone), helicity is a topological invariant closely related to the knottedness of vortex lines (Moffatt 1969 J. Fluid Mech. 35 (1), 117–129). Helicity is conserved following a material volume for compact vorticity distributions, i.e. when the vorticity field is tangent to the surface of the volume. There is a related helicity invariant in ideal magnetohydrodynamics involving the correlation between the magnetic potential and its curl, the magnetic field. Helicity is a fragile invariant in the sense that relaxing any one of the ideal conditions results in non-conservation. Unlike energy and enstrophy (mean-square vorticity), helicity is not positive (or sign) definite. Viscous diffusion can create both positive and negative helicity when vortex lines reconnect, something which is topologically forbidden in an ideal fluid where vortex lines move as material curves. Moreover, variable density or more generally compressibility destroys conservation and weakens the association between helicity and vortex-line topology. Furthermore, in compressible flows, the velocity field is not entirely determined from the vorticity field. A recent paper by Boutros & Gibbon (2025) J. Fluid Mech. in this journal explains how one can extend the definition of helicity to control and limit the non-conservation of helicity. This offers a promising way forward in using helicity to characterise flow properties in computational studies of high Reynolds number flows.

This study investigates the energy exchange between coherent structures in flows over four low-aspect-ratio (low-) plates using the tomographic particle image velocimetry dataset originally obtained by Zhu et al. (2024. J. Fluid Mech. 983, A35). The chord-based Reynolds number is $5400$, with fixed angle of attack $6 ^\circ$. In this study, multiscale proper orthogonal decomposition is applied to extract the coherent structures, including those associated with the vortex-shedding frequency $St_1$ and its subharmonic counterpart. Subsequently, the coherent kinetic energy budget is analysed with a focus on inter-scale energy transfer. This study demonstrates that the energy transfer between the scales centred at $St_1$ and $0.5\,St_1$ can exhibit a reverse or forward direction, depending on the transformation pattern of the leading-edge vortices (LEVs). Specifically, different triadic interactions are excited during the LEV transformation, and manifest themselves during the formation of hairpin vortices downstream. Understanding this nonlinear energy transfer is essential for elucidating mechanisms underlying the development of turbulence in three-dimensional flows over low- plates.

Droplet coalescence is an essential multiphase flow process in nature and industry. For the inviscid coalescence of two spherical droplets, our experiment shows that the classical 1/2 power-law scaling for equal-size droplets still holds for the unequal-size situation of small size ratios, but it diverges as the size ratio increases. Employing an energy balance analysis, we develop the first theory for asymmetric droplet coalescence, yielding a solution that collapses all experimental data of different size ratios. This confirms the physical relevance of the new set of length and time scales given by the theory. The functionality of the solution reveals an exponential dependence of the bridge’s radial growth on time, implying a scaling-free nature. Nevertheless, the small-time asymptote of the model is able to recover the classical power-law scaling, so that the actual bridge evolution still follows the scaling law asymptotically in a wide parameter space. Further analysis suggests that the scaling-free evolution behaviour emerges only at late coalescence time and large size ratios.

The flow behind impulsively started circular and polygonal plates is investigated experimentally, using particle image velocimetry at several azimuthal angles. Observing plates accelerating up to a steady Reynolds number $Re=27\,000$, the three invariants of the motion, circulation $\Gamma$, hydrodynamic impulse $I$ and kinetic energy $E$, were scaled against four candidate lengths: the hydraulic diameter, perimeter, circumscribed diameter and the square root of the area. Of these, the square root of the area was found to best collapse all the data. Investigating the three-dimensionality of the flow, it is found that, while a single-plane measurement can provide a reasonable approximation for $\Gamma$ behind plates, multiple planes are necessary to accurately estimate $E$ and $I$.

The linear and nonlinear dynamics of centrifugal instability in Taylor–Couette flow are investigated when fluids are stably stratified and highly diffusive. One-dimensional local linear stability analysis (LSA) of cylindrical Couette flow confirms that the stabilising role of stratification in centrifugal instability is suppressed by strong thermal diffusion (i.e. low Prandtl number $Pr$). For $Pr\ll 1$, it is verified that the instability dependence on thermal diffusion and stratification with the non-dimensional Brunt–Väisälä frequency $N$ can be prescribed by a single rescaled parameter $P_{N}=N^{2}Pr$. From direct numerical simulation (DNS), various nonlinear features such as axisymmetric Taylor vortices at saturation, secondary instability leading to non-axisymmetric patterns or transition to chaotic states are investigated for various values of $Pr\leqslant 1$ and Reynolds number $Re_{i}$. Two-dimensional bi-global LSA of axisymmetric Taylor vortices, which appear as primary centrifugal instability saturates nonlinearly, is also performed to find the secondary critical Reynolds number $Re_{i,2}$ at which the Taylor vortices become unstable by non-axisymmetric perturbation. The bi-global LSA reveals that $Re_{i,2}$ increases (i.e. the onset of secondary instability is delayed) in the range $10^{-3}\lt Pr\lt 1$ at $N=1$ or as $N$ increases at $Pr=0.01$. Secondary instability leading to highly non-axisymmetric or irregular chaotic patterns is further investigated by three-dimensional DNS. The Nusselt number $Nu$ is also computed from the torque at the inner cylinder for various $Pr$ and $Re_{i}$ at $N=1$ to describe how the angular momentum transfer increases with $Re_{i}$ and how $Nu$ varies differently for saturated and chaotic states.

In marine and offshore engineering, the presence of air in the water plays a significant role in influencing impact pressures during water entry events. Owing to limited research on the impact loads of aerated water entry, this study aims to explore the effect of aeration on water entry impact pressures. A comprehensive experimental investigation on pure and aerated water entry of a wedge with a 20° deadrise angle was presented. The wire-mesh sensor (WMS) technology was proposed to accurately quantify the spatial and temporal distributions of void fractions in multiphase environments. The WMS provides reliable and consistent measurements at varying void fractions, as validated against image-based methods. The results indicated that the aeration reduced peak impact pressures by up to 33 %, and extended pressure duration, with a linear relationship between impact pressure and void fraction. Furthermore, the probability distribution of peak pressures conformed well to both the generalised extreme value and Weibull distributions, with the void fraction exerting a strong influence on pressure distribution parameters. These findings suggest that controlled aeration can effectively mitigate impact loads, offering practical implications for marine structure design.

Bubble bursting and subsequent collapse of the open cavity at free surfaces of contaminated liquids can generate aerosol droplets, facilitating pathogen transport. After film rupture, capillary waves focus at the cavity base, potentially generating fast Worthington jets that are responsible for ejecting the droplets away from the source. While extensively studied for Newtonian fluids, the influence of non-Newtonian rheology on this process remains poorly understood. Here, we employ direct numerical simulations to investigate the bubble cavity collapse in viscoelastic media, such as polymeric liquids. We find that the jet and drop formations are dictated by two dimensionless parameters: the elastocapillary number 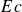$Ec$ (the ratio of the elastic modulus and the Laplace pressure) and the Deborah number $De$ (the ratio of the relaxation time and the inertio-capillary time scale). We show that, for low values of 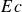$Ec$ and $De$, the viscoelastic liquid adopts a Newtonian-like behaviour, where the dynamics is governed by the solvent Ohnesorge number $Oh_s$ (the ratio of visco-capillary and inertio-capillary time scales). In contrast, for large values 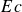$Ec$ and $De$, the enhanced elastic stresses completely suppress the formation of the jet. For some cases with intermediate values of $Ec$ and $De$, smaller droplets are produced compared with Newtonian fluids, potentially enhancing aerosol dispersal. By mapping the phase space spanned by 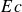$Ec$, 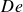$De$ and $Oh_s$, we reveal three distinct flow regimes: (i) jets forming droplets, (ii) jets without droplet formation and (iii) absence of jet formation. Our results elucidate the mechanisms underlying aerosol suppression versus fine spray formation in polymeric liquids, with implications for pathogen transmission and industrial processes involving viscoelastic fluids.

The propulsive efficiency of flying and swimming animals propelled by oscillatory appendages typically peaks within a narrow Strouhal number range of $0.20 \lt St \lt 0.40$. Motivated by the ubiquitous presence of stratification in natural environments, we numerically investigate the optimal Strouhal numbers $S{t_m}$ for an oscillating foil in density stratified fluids. Our results reveal that $S{t_m}$ increases with the strength of stratification characterised by the internal Froude number $Fr$, giving rise to markedly higher values under strong stratifications compared with those observed in homogeneous fluids. The propulsive efficiency tends to maximise when there is a resonance between the oscillations of the foil and the fluid, as inferred from a fitted line in the ($St$, $Fr$) parameter space, which shows that $S{t_m}$ is proportional to $Fr^{-1}$. We further uncover that the significant increase in $S{t_m}$ in strongly stratified regimes is fundamentally driven by fluid entrainment. During this process, the oscillating foil induces perturbations in the density field, resulting in buoyancy-driven restoring forces which alter the pressure distribution on the foil and thus the hydrodynamic forces. Notably, only under strongly stratified conditions, where dominant buoyancy effects confine the density transport to the vicinity of the oscillating foil, the intensified density perturbation due to the increase in $St$ can be effectively harnessed to enhance thrust production, thereby contributing to the elevated $S{t_m}$. These insights suggest that oscillatory propulsors should adopt new kinematic strategies involving relatively large Strouhal numbers to achieve efficient cruising in strongly stratified environments.

Recent experimental studies reveal that the near-wake region of a circular cylinder at hypersonic Mach numbers exhibits self-sustained flow oscillations. The oscillation frequency was found to have a universal behaviour. These oscillations are of a fundamentally different nature in comparison with flow oscillations caused due to vortex shedding, which are commonly observed in cylinder wakes at low-subsonic Mach numbers. The experimental observations suggest an aeroacoustic feedback loop to be the driving mechanism of the oscillations at high Mach numbers. An analytical aeroacoustic model that successfully predicts the experimentally observed frequencies and explains the universal behaviour is presented here. The model provides physical insights into and informs us of flow regimes where deviations from universal behaviour are to be expected. These findings hold relevance for a wider class of non-canonical wake flows at high Mach numbers.

We present a mathematical model to investigate heat transfer and mass transport dynamics in the wave-driven free-surface boundary layer of the ocean under the influence of long-crested progressive surface gravity waves. The continuity, momentum and convection–diffusion equations for fluid temperature are solved within a Lagrangian framework. We assume that eddy viscosity and thermometric conductivity are dependent on Lagrangian coordinates, and derive a new form of the second-order Lagrangian mass transport velocity, applicable across the entire finite water depth. We then analyse the convective heat dynamics influenced by the free-surface boundary layer. Rectangular distributions of free-surface temperature (i.e. a Dirichlet boundary condition) are considered, and analytical solutions for thermal boundary layer temperature fields are provided to offer insights into free-surface heat transfer mechanisms affected by ocean waves. Our results suggest the need to improve existing models that neglect the effects of free-surface waves and the free-surface boundary layer on ocean mass transport and heat transfer.

Starting from the coupled Boltzmann–Enskog (BE) kinetic equations for a two-particle system consisting of hard spheres, a hyperbolic two-fluid model for binary, hard-sphere mixtures was derived in Fox (2019, J. Fluid Mech. 877, 282). In addition to spatial transport, the BE kinetic equations account for particle–particle collisions, using an elastic hard-sphere collision model, and the Archimedes (buoyancy) force due to spatial gradients of the pressure in each phase, as well as other forces involving spatial gradients. The ideal-fluid–particle limit of this model is found by letting one of the particle diameters go to zero while the other remains finite. The resulting two-fluid model has closed terms for the spatial fluxes and momentum exchange due to the excluded volume occupied by the particles, e.g. a momentum-exchange term $\boldsymbol {F}_{\!\!fp}$ that depends on gradients of the fluid density $\rho _f$, fluid velocity $\boldsymbol{u}_{f}$ and fluid pressure $p_f$. In Zhang et al. (2006, Phy. Rev. Lett. 97, 048301), the corresponding unclosed momentum-exchange term depends on the divergence of an unknown particle–fluid–particle (pfp) stress (or pressure) tensor. Here, it is shown that the pfp-pressure tensor ${\unicode{x1D64B}}_{\!pfp}$ can be found in closed form from the expression for $\boldsymbol {F}_{\!\!fp}$ derived in Fox (2019, J. Fluid Mech. 877, 282). Remarkably, using this expression for ${\unicode{x1D64B}}_{\!pfp}$ ensures that the two-fluid model for ideal-fluid–particle flow is well posed for all fluid-to-particle material-density ratios $Z = \rho _f / \rho _p$.

It is known that the complex eigenfrequencies of one-dimensional systems of large but finite extent are concentrated near the asymptotic curve determined by the dispersion relation of an infinite system. The global instability caused by uppermost pieces of this curve was studied in various problems, including hydrodynamic stability and fluid–structure interaction problems. In this study, we generalise the equation for the asymptotic curve to arbitrary frequencies. We analyse stable local topology of the curve and prove that it can be a regular point, branching point or dead-end point of the curve. We give a classification of unstable local tolopogies, and show how they break up due to small changes of the problem parameters. The results are demonstrated on three examples: supersonic panel flutter, flutter of soft fluid-conveying pipe, and the instability of rotating flow in a pipe. We show how the elongation of the system yields the attraction of the eigenfrequencies to the asymptotic curve, and how each locally stable curve topology is reflected on the interaction of eigenfrequencies.

We study the near-wall behaviour of pressure spectra and associated variances in canonical wall-bounded flows, with a special focus on pipe flow. Analysis of the pressure spectra reveals the universality of small and large scales, supporting the establishment of $ k^{-1}$ spectral layers as predicted by fundamental physical theories. However, this universality does not extend to the velocity spectra (Pirozzoli, J. Fluid Mech., vol. 989, 2024, A5), which show a lack of universality at the large-scale end and systematic deviations from the $ k^{-1}$ behaviour. We attribute this fundamental difference to the limited influence of direct viscous effects on pressure, with implied large differences in the near-wall behaviour. Consequently, the inner-scaled pressure variances continue to increase logarithmically with the friction Reynolds number as we also infer from a refined version of the attached-eddy model, while the growth of the velocity variance tends to saturate. Extrapolated distributions of the pressure variance at extremely high Reynolds numbers are inferred.

Understanding the vertical coherence of the pressure structure and its interaction with velocity fields is critical for elucidating the mechanisms of acoustic generation and radiation in hypersonic turbulent boundary layers. This study employs linear coherence analysis to examine the self-similar coherent structures in the velocity and pressure fields within a Mach 6 hypersonic boundary layer, considering a range of wall-to-recovery temperature ratios. The influence of wall cooling on the geometric characteristics of these structures, such as inclination angles and three-dimensional aspect ratios, is evaluated. Specifically, the streamwise velocity exhibits self-similar coherent structures with the streamwise/wall-normal aspect ratio ranging from 16.5 to 38.7, showing a linear increases with decreasing wall temperatures. Similar linear dependence between the streamwise/wall-normal aspect ratio and the wall temperatures are observed for the Helmholtz-decomposed streamwise velocity and the pressure field. In terms of velocity–pressure coupling, the solenoidal component exhibits stronger interactions with the pressure fields in the near-wall region, while the dilatational component has stronger interactions with the pressure field at large scales with the increase of height. Such coupling generally follows the distance-from-the-wall scaling of the pressure field, except in cooled wall cases. Using the linear stochastic estimation, the pressure field across the boundary layer is predicted by inputting the near-wall pressure/velocity signal along with the transfer kernel. The result demonstrates that near-wall pressure signals provide the most accurate description of the pressure field in higher regions of the boundary layer. As wall-mounted sensors can measure near-wall pressure fluctuations, this study presents a potential approach to predict the off-wall pressure field correlated with the near-wall structures based on wall-pressure measurements.

We conduct direct numerical simulations to investigate the synchronisation of Kolmogorov flows in a periodic box, with a focus on the mechanisms underlying the asymptotic evolution of infinitesimal velocity perturbations, also known as conditional leading Lyapunov vectors. This study advances previous work with a spectral analysis of the perturbation, which clarifies the behaviours of the production and dissipation spectra at different coupling wavenumbers. We show that, in simulations with moderate Reynolds numbers, the conditional leading Lyapunov exponent can be smaller than a lower bound proposed previously based on a viscous estimate. A quantitative analysis of the self-similar evolution of the perturbation energy spectrum is presented, extending the existing qualitative discussion. The prerequisites for obtaining self-similar solutions are established, which include an interesting relationship between the integral length scale of the perturbation velocity and the local Lyapunov exponent. By examining the governing equation for the dissipation rate of the velocity perturbation, we reveal the previously neglected roles of the strain rate and vorticity perturbations, and uncover their unique geometrical characteristics.

History effects play a significant role in determining the velocity in boundary layers with pressure gradients, complicating the identification of a velocity scaling. This work pivots away from traditional velocity analysis to focus on fluid acceleration in boundary layers with strong adverse pressure gradients. We draw parallels between the transport equation of the velocity in an equilibrium spatially evolving boundary layer and the transport equation of the fluid acceleration in temporally evolving boundary layers with pressure gradients, establishing an analogy between the two. To validate our analogy, we show that the laminar Stokes solution, which describes the flow immediately after the application of a pressure gradient force, is consistent with the present analogy. Furthermore, fluid acceleration exhibits a linear scaling in the wall layer and transitions to logarithmic scaling away from the wall after the initial period, mirroring the velocity in an equilibrium boundary layer, lending further support to the analogy. Finally, by integrating fluid acceleration, a velocity scaling is derived, which compares favourably with data as well.

The Reynolds number dependence of the normalised energy dissipation rate $C_{\epsilon }=\epsilon L/u^3$ is studied, where $\epsilon$ is the energy dissipation rate, $L$ is the integral length scale and $u$ is the root-mean-square velocity. We present the derivation of the exact relationship between the normalised energy dissipation rate and integrated form of the Kármán–Howarth equation in homogeneous isotropic turbulence. The present mathematical formulation is valid for both forced and decaying turbulence. The discussion of $C_{\epsilon }$ is developed under the assumption that the term resulting from the nonlinear energy transfer appearing in $C_{\epsilon }$ is constant at sufficiently high-Reynolds-number turbulence. The fact that the integrated term originating from nonlinear energy transfer is constant plays the role of a lower bound in $C_{\epsilon }$, implying that the energy dissipation rate is finite in high-Reynolds-number turbulence. Furthermore, the origin of the non-equilibrium dissipation law could be the imbalance between $u$ and ${\rm d}L/{\rm d}t$, the influence of external forces, or both. In decaying turbulence with forced turbulence as the initial condition, the imbalance between $u$ and ${\rm d}L/{\rm d}t$ causes the non-equilibrium dissipation law. The validity of the theoretical analysis is investigated using direct numerical simulations of the forced and decaying turbulence.

We study the evaporation dynamics of non-thin non-spherical-cap (i.e. wavy) droplets. These droplets exhibit surface curvature that varies periodically with the polar angle, which profoundly influences their evaporation flux, internal flow dynamics, and the resultant deposition patterns upon complete evaporation. The droplet is considered quasi-static throughout its entire lifetime. The asymptotic expansions of the evaporation flux in the diffusion-limited model, and the induced internal inviscid flow of the droplets, are derived through asymptotic analysis. Under the assumption of small deformation amplitudes, the accuracies of these two expansions are validated numerically. Expanding upon these asymptotic results, we also investigate the surface density profile of the droplet deposition after it dries up. The results indicate that the freely moving contact line of the droplet leads to the deposited stain exhibiting a mountain-like morphology. The internal inviscid flow along with the non-spherical-cap shape eliminates the divergence of the deposited surface density profile at droplet’s centre. This work provides a theoretical basis for geometrically controlled sessile droplet evaporation, which may have practical applications in industry.

This investigation examines the dynamic response of an accelerating turbulent pipe flow using direct numerical simulation data sets. A low/high-pass Fourier filter is used to investigate the contribution and time dependence of the large-scale motions (LSM) and the small-scale motions (SSM) into the transient Reynolds shear stress. Additionally, it analyses how the LSM and SSM influence the mean wall shear stress using the Fukagata–Iwamoto–Kasagi identity. The results reveal that turbulence is frozen during the early flow excursion. During the pretransition stage, energy growth of the LSM and a subtle decay in the SSM is observed, suggesting a laminarescent trend of SSM. The transition period exhibits rapid energy growth in the SSM energy spectrum at the near-wall region, implying a shift in the dominant contribution from LSM to SSM to the frictional drag. The core-relaxation stage shows a quasisteady behaviour in large- and small-scale turbulence at the near-wall region and progressive growth of small- and large-scale turbulence within the wake region. The wall-normal gradient of the Reynolds shear stress premultiplied energy cospectra was analysed to understand how LSM and SSM influence the mean momentum balance across the different transient stages. A relevant observation is the creation of a momentum sink produced at the buffer region in large- and very large-scale (VLSM) wavelengths during the pretransition. This sink region annihilates a momentum source located in the VLSM spectrum and at the onset of the logarithmic region of the net-force spectra. This region is a source term in steady wall-bounded turbulence.