We present a systematic study on the effects of small aspect ratios 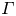 $\varGamma$ on heat transport in liquid metal convection with a Prandtl number of
$\varGamma$ on heat transport in liquid metal convection with a Prandtl number of 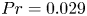 $Pr=0.029$. The study covers
$Pr=0.029$. The study covers 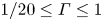 $1/20\le \varGamma \le 1$ experimentally and
$1/20\le \varGamma \le 1$ experimentally and 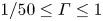 $1/50\le \varGamma \le 1$ numerically, and a Rayleigh number
$1/50\le \varGamma \le 1$ numerically, and a Rayleigh number 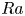 $Ra$ range of
$Ra$ range of 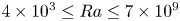 $4\times 10^3 \le Ra \le 7\times 10^{9}$. It is found experimentally that the local effective heat transport scaling exponent
$4\times 10^3 \le Ra \le 7\times 10^{9}$. It is found experimentally that the local effective heat transport scaling exponent 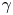 $\gamma$ changes with both
$\gamma$ changes with both 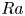 $Ra$ and
$Ra$ and 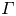 $\varGamma$, attaining a
$\varGamma$, attaining a 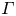 $\varGamma$-dependent maximum value before transition-to-turbulence and approaches
$\varGamma$-dependent maximum value before transition-to-turbulence and approaches 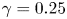 $\gamma =0.25$ in the turbulence state as
$\gamma =0.25$ in the turbulence state as 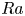 $Ra$ increases. Just above the onset of convection, Shishkina (Phys. Rev. Fluids, vol 6, 2021, 090502) derived a length scale
$Ra$ increases. Just above the onset of convection, Shishkina (Phys. Rev. Fluids, vol 6, 2021, 090502) derived a length scale 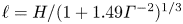 $\ell =H/(1+1.49\varGamma ^{-2})^{1/3}$. Our numerical study shows
$\ell =H/(1+1.49\varGamma ^{-2})^{1/3}$. Our numerical study shows 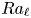 $Ra_{\ell }$, i.e.
$Ra_{\ell }$, i.e. 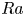 $Ra$ based on
$Ra$ based on 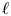 $\ell$, serves as a proper control parameter for heat transport above the onset with
$\ell$, serves as a proper control parameter for heat transport above the onset with 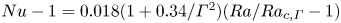 $Nu-1=0.018(1+0.34/\varGamma ^2)(Ra/Ra_{c,\varGamma }-1)$. Here
$Nu-1=0.018(1+0.34/\varGamma ^2)(Ra/Ra_{c,\varGamma }-1)$. Here 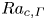 $Ra_{c,\varGamma }$ represents the
$Ra_{c,\varGamma }$ represents the 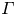 $\varGamma$-dependent critical
$\varGamma$-dependent critical 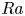 $Ra$ for the onset of convection and
$Ra$ for the onset of convection and 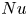 $Nu$ is the Nusselt number. In the turbulent state, for a general scaling law of
$Nu$ is the Nusselt number. In the turbulent state, for a general scaling law of 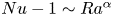 $Nu-1\sim Ra^\alpha$, we propose a length scale
$Nu-1\sim Ra^\alpha$, we propose a length scale 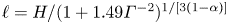 $\ell = H/(1+1.49\varGamma ^{-2})^{1/[3(1-\alpha )]}$. In the case of turbulent liquid metal convection with
$\ell = H/(1+1.49\varGamma ^{-2})^{1/[3(1-\alpha )]}$. In the case of turbulent liquid metal convection with 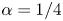 $\alpha =1/4$, our measurement shows that the heat transport will become weakly dependent on
$\alpha =1/4$, our measurement shows that the heat transport will become weakly dependent on 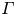 $\varGamma$ with
$\varGamma$ with 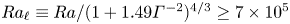 $Ra_{\ell }\equiv Ra/(1+1.49\varGamma ^{-2})^{4/3} \ge 7\times 10^5$. Finally, once the flow becomes time-dependent, the growth rate of
$Ra_{\ell }\equiv Ra/(1+1.49\varGamma ^{-2})^{4/3} \ge 7\times 10^5$. Finally, once the flow becomes time-dependent, the growth rate of 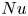 $Nu$ with
$Nu$ with 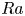 $Ra$ declines compared with the linear growth rate in the convection state. A hysteresis is observed in a
$Ra$ declines compared with the linear growth rate in the convection state. A hysteresis is observed in a 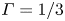 $\varGamma =1/3$ cell when the flow becomes time-dependent. Measurements of the large-scale circulation suggest the hysteresis is caused by the system switching from a single-roll-mode to a double-roll-mode in an oscillation state.
$\varGamma =1/3$ cell when the flow becomes time-dependent. Measurements of the large-scale circulation suggest the hysteresis is caused by the system switching from a single-roll-mode to a double-roll-mode in an oscillation state.