We show that every $(n,d,\lambda )$-graph contains a Hamilton cycle for sufficiently large $n$, assuming that $d\geq \log ^{6}n$ and $\lambda \leq cd$, where $c=\frac {1}{70000}$. This significantly improves a recent result of Glock, Correia, and Sudakov, who obtained a similar result for $d$ that grows polynomially with $n$. The proof is based on a new result regarding the second largest eigenvalue of the adjacency matrix of a subgraph induced by a random subset of vertices, combined with a recent result on connecting designated pairs of vertices by vertex-disjoint paths in $(n,d,\lambda )$-graphs. We believe that the former result is of independent interest and will have further applications.

A tantalizing open problem, posed independently by Stiebitz in 1995 and by Alon in 1996 and again in 2006, asks whether for every pair of integers 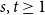$s,t \ge 1$ there exists a finite number 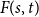$F(s,t)$ such that the vertex set of every digraph of minimum out-degree at least 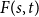$F(s,t)$ can be partitioned into non-empty parts 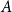$A$ and 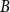$B$ such that the subdigraphs induced on 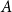$A$ and 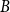$B$ have minimum out-degree at least $s$ and 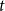$t$, respectively.

In this short note, we prove that if 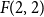$F(2,2)$ exists, then all the numbers 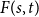$F(s,t)$ with 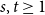$s,t\ge 1$ exist and satisfy 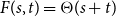$F(s,t)=\Theta (s+t)$. In consequence, the problem of Alon and Stiebitz reduces to the case 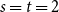$s=t=2$. Moreover, the numbers 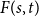$F(s,t)$ with 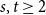$s,t \ge 2$ either all exist and grow linearly, or all of them do not exist.

This paper initiates the explicit study of face numbers of matroid polytopes and their computation. We prove that, for the large class of split matroid polytopes, their face numbers depend solely on the number of cyclic flats of each rank and size, together with information on the modular pairs of cyclic flats. We provide a formula which allows us to calculate $f$-vectors without the need of taking convex hulls or computing face lattices. We discuss the particular cases of sparse paving matroids and rank two matroids, which are of independent interest due to their appearances in other combinatorial and geometric settings.

In this note, we formulate a ‘one-sided’ version of Wormald’s differential equation method. In the standard ‘two-sided’ method, one is given a family of random variables that evolve over time and which satisfy some conditions, including a tight estimate of the expected change in each variable over one-time step. These estimates for the expected one-step changes suggest that the variables ought to be close to the solution of a certain system of differential equations, and the standard method concludes that this is indeed the case. We give a result for the case where instead of a tight estimate for each variable’s expected one-step change, we have only an upper bound. Our proof is very simple and is flexible enough that if we instead assume tight estimates on the variables, then we recover the conclusion of the standard differential equation method.

We consider the hard-core model on a finite square grid graph with stochastic Glauber dynamics parametrized by the inverse temperature $\beta$. We investigate how the transition between its two maximum-occupancy configurations takes place in the low-temperature regime $\beta \to \infty$ in the case of periodic boundary conditions. The hard-core constraints and the grid symmetry make the structure of the critical configurations for this transition, also known as essential saddles, very rich and complex. We provide a comprehensive geometrical characterization of these configurations that together constitute a bottleneck for the Glauber dynamics in the low-temperature limit. In particular, we develop a novel isoperimetric inequality for hard-core configurations with a fixed number of particles and show how the essential saddles are characterized not only by the number of particles but also their geometry.

In the last two decades the study of random instances of constraint satisfaction problems (CSPs) has flourished across several disciplines, including computer science, mathematics and physics. The diversity of the developed methods, on the rigorous and non-rigorous side, has led to major advances regarding both the theoretical as well as the applied viewpoints. Based on a ceteris paribus approach in terms of the density evolution equations known from statistical physics, we focus on a specific prominent class of regular CSPs, the so-called occupation problems, and in particular on $r$-in-$k$ occupation problems. By now, out of these CSPs only the satisfiability threshold – the largest degree for which the problem admits asymptotically a solution – for the $1$-in-$k$ occupation problem has been rigorously established. Here we determine the satisfiability threshold of the $2$-in-$k$ occupation problem for all $k$. In the proof we exploit the connection of an associated optimization problem regarding the overlap of satisfying assignments to a fixed point problem inspired by belief propagation, a message passing algorithm developed for solving such CSPs.

For a given graph $H$, we say that a graph $G$ has a perfect $H$-subdivision tiling if $G$ contains a collection of vertex-disjoint subdivisions of $H$ covering all vertices of $G.$ Let $\delta _{\mathrm {sub}}(n, H)$ be the smallest integer $k$ such that any $n$-vertex graph $G$ with minimum degree at least $k$ has a perfect $H$-subdivision tiling. For every graph $H$, we asymptotically determined the value of $\delta _{\mathrm {sub}}(n, H)$. More precisely, for every graph $H$ with at least one edge, there is an integer $\mathrm {hcf}_{\xi }(H)$ and a constant $1 \lt \xi ^*(H)\leq 2$ that can be explicitly determined by structural properties of $H$ such that $\delta _{\mathrm {sub}}(n, H) = \left (1 - \frac {1}{\xi ^*(H)} + o(1) \right )n$ holds for all $n$ and $H$ unless $\mathrm {hcf}_{\xi }(H) = 2$ and $n$ is odd. When $\mathrm {hcf}_{\xi }(H) = 2$ and $n$ is odd, then we show that $\delta _{\mathrm {sub}}(n, H) = \left (\frac {1}{2} + o(1) \right )n$.

For each uniformity $k \geq 3$, we construct $k$ uniform linear hypergraphs $G$ with arbitrarily large maximum degree $\Delta$ whose independence polynomial $Z_G$ has a zero $\lambda$ with $\left \vert \lambda \right \vert = O\left (\frac {\log \Delta }{\Delta }\right )$. This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.

Structural convergence is a framework for the convergence of graphs by Nešetřil and Ossona de Mendez that unifies the dense (left) graph convergence and Benjamini-Schramm convergence. They posed a problem asking whether for a given sequence of graphs $(G_n)$ converging to a limit $L$ and a vertex $r$ of $L$, it is possible to find a sequence of vertices $(r_n)$ such that $L$ rooted at $r$ is the limit of the graphs $G_n$ rooted at $r_n$. A counterexample was found by Christofides and Král’, but they showed that the statement holds for almost all vertices $r$ of $L$. We offer another perspective on the original problem by considering the size of definable sets to which the root $r$ belongs. We prove that if $r$ is an algebraic vertex (i.e. belongs to a finite definable set), the sequence of roots $(r_n)$ always exists.

We prove a new lower bound for the almost 20-year-old problem of determining the smallest possible size of an essential cover of the $n$-dimensional hypercube $\{\pm 1\}^n$, that is, the smallest possible size of a collection of hyperplanes that forms a minimal cover of $\{\pm 1\}^n$ and such that, furthermore, every variable appears with a non-zero coefficient in at least one of the hyperplane equations. We show that such an essential cover must consist of at least $10^{-2}\cdot n^{2/3}/(\log n)^{2/3}$ hyperplanes, improving previous lower bounds of Linial–Radhakrishnan, of Yehuda–Yehudayoff, and of Araujo–Balogh–Mattos.

In this paper we consider positional games where the winning sets are edge sets of tree-universal graphs. Specifically, we show that in the unbiased Maker-Breaker game on the edges of the complete graph $K_n$, Maker has a strategy to claim a graph which contains copies of all spanning trees with maximum degree at most $cn/\log (n)$, for a suitable constant $c$ and $n$ being large enough. We also prove an analogous result for Waiter-Client games. Both of our results show that the building player can play at least as good as suggested by the random graph intuition. Moreover, they improve on a special case of earlier results by Johannsen, Krivelevich, and Samotij as well as Han and Yang for Maker-Breaker games.

We show that the twin-width of every $n$-vertex $d$-regular graph is at most $n^{\frac{d-2}{2d-2}+o(1)}$ for any fixed integer $d \geq 2$ and that almost all $d$-regular graphs attain this bound. More generally, we obtain bounds on the twin-width of sparse Erdős–Renyi and regular random graphs, complementing the bounds in the denser regime due to Ahn, Chakraborti, Hendrey, Kim, and Oum.

We consider the performance of Glauber dynamics for the random cluster model with real parameter $q\gt 1$ and temperature $\beta \gt 0$. Recent work by Helmuth, Jenssen, and Perkins detailed the ordered/disordered transition of the model on random $\Delta$-regular graphs for all sufficiently large $q$ and obtained an efficient sampling algorithm for all temperatures $\beta$ using cluster expansion methods. Despite this major progress, the performance of natural Markov chains, including Glauber dynamics, is not yet well understood on the random regular graph, partly because of the non-local nature of the model (especially at low temperatures) and partly because of severe bottleneck phenomena that emerge in a window around the ordered/disordered transition. Nevertheless, it is widely conjectured that the bottleneck phenomena that impede mixing from worst-case starting configurations can be avoided by initialising the chain more judiciously. Our main result establishes this conjecture for all sufficiently large $q$ (with respect to $\Delta$). Specifically, we consider the mixing time of Glauber dynamics initialised from the two extreme configurations, the all-in and all-out, and obtain a pair of fast mixing bounds which cover all temperatures $\beta$, including in particular the bottleneck window. Our result is inspired by the recent approach of Gheissari and Sinclair for the Ising model who obtained a similar flavoured mixing-time bound on the random regular graph for sufficiently low temperatures. To cover all temperatures in the RC model, we refine appropriately the structural results of Helmuth, Jenssen and Perkins about the ordered/disordered transition and show spatial mixing properties ‘within the phase’, which are then related to the evolution of the chain.