Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T23:04:17.165Z Has data issue: false hasContentIssue false
  • English
  • Français

Structural convergence and algebraic roots

Part of: Miscellaneous topics in measure theory Graph theory Model theory

Published online by Cambridge University Press:  23 December 2024

David Hartman Open the ORCID record for David Hartman [Opens in a new window] ,
Tomáš Hons Open the ORCID record for Tomáš Hons [Opens in a new window]  and
Jaroslav Nešetřil Open the ORCID record for Jaroslav Nešetřil [Opens in a new window]
David Hartman*
Affiliation:
Computer Science Institute, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic
Tomáš Hons
Affiliation:
Computer Science Institute, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
Jaroslav Nešetřil
Affiliation:
Computer Science Institute, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
*
Corresponding author: David Hartman; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Structural convergence is a framework for the convergence of graphs by Nešetřil and Ossona de Mendez that unifies the dense (left) graph convergence and Benjamini-Schramm convergence. They posed a problem asking whether for a given sequence of graphs 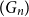$(G_n)$ converging to a limit 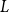$L$ and a vertex $r$ of 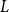$L$, it is possible to find a sequence of vertices 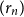$(r_n)$ such that 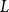$L$ rooted at $r$ is the limit of the graphs 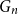$G_n$ rooted at 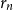$r_n$. A counterexample was found by Christofides and Král’, but they showed that the statement holds for almost all vertices $r$ of 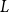$L$. We offer another perspective on the original problem by considering the size of definable sets to which the root $r$ belongs. We prove that if $r$ is an algebraic vertex (i.e. belongs to a finite definable set), the sequence of roots 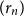$(r_n)$ always exists.

Keywords

Structural convergencegraph limitsrooting verticesalgebraic sets

MSC classification

Primary: 03C98: Applications of model theory 05C63: Infinite graphs
Secondary: 28E15: Other connections with logic and set theory
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Benjamini, I. and Schramm, O. (2001) Recurrence of Distributional Limits of Finite Planar Graphs. Electron. J. Probab. 6 1–13. DOI: 10.1214/ejp.v6-96 CrossRefGoogle Scholar
Borgs, C., Chayes, J., Lovász, L., Sós, V. T. and Vesztergombi, K. (2006) ”Counting Graph Homomorphisms”. In: Topics in Discrete Mathematics. Berlin Heidelberg: Springer, pp. 315–371. DOI: 10.1007/3-540-33700-8_18. 978-3-540-33700-3CrossRefGoogle Scholar
Christofides, D. and Král’, D. (2015) First-Order Convergence and Roots. Combin. Probab. Comput. 25 213–221. DOI: 10.1017/s0963548315000048 CrossRefGoogle Scholar
Elek, G. (2007) Note on limits of finite graphs. Combinatorica 27 503–507. DOI: 10.1007/s00493-007-2214-8 CrossRefGoogle Scholar
Hartman, D., Hons, T. and Nešetřil, J. (2022) Gadget construction and structural convergence. https://arxiv.org/abs/2212.10985 Google Scholar
Hartman, D., Hons, T. and Nešetřil, J. (2023) Rooting algebraic vertices of convergent sequences. In Proceedings of the 12th European Conference on Combinatorics, Graph Theory and Applications. Masaryk University Press, pp. 539–544. DOI: 10.5817/cz.muni.eurocomb23-075 CrossRefGoogle Scholar
Hodges, W. (1993) Model Theory. Cambridge University Press, DOI: 10.1017/cbo9780511551574 CrossRefGoogle Scholar
Lovász, L. (2012) Large networks and graph limits.American Mathematical Society, 9780821890851CrossRefGoogle Scholar
Lovász, L. and Szegedy, B. (2006) Limits of dense graph sequences. J. Comb. Theory Series B 96 933–957. DOI: 10.1016/j.jctb.2006.05.002 CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O. (2020) “A Unified Approach to Structural Limits and Limits of Graphs with Bounded Tree-Depth”. Memoirs of the American Mathematical Society, 263. DOI: 10.1090/memo/1272 Google Scholar
Nešetřil, J. and de Mendez, P. O. (2017) Cluster analysis of local convergent sequences of structures. Random Struct. Algor. 51, 674–728. DOI: 10.1002/rsa.20719 CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O. (2019) Existence of Modeling Limits for Sequences of Sparse Structures. J. Symb. Log. 84, 452–472. DOI: 10.1017/jsl.2018.32 CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O. (2012) Sparsity. Springer: Berlin Heidelberg, DOI: 10.1007/978-3-642-27875-4 CrossRefGoogle Scholar
Stanley, R. P. and Fomin, S. (1999) Enumerative Combinatorics. Cambridge University Press, DOI: 10.1017/cbo9780511609589 CrossRefGoogle Scholar
Tent, K. and Ziegler, M. (2012) A Course in Model Theory. Cambridge University Press, DOI: 10.1017/cbo9781139015417 CrossRefGoogle Scholar
Whitney, Hassler (1972) Complex Analytic Varieties. Addsion Wesley Longman Publishing Group, pp. 399.9780201086539Google Scholar