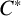 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
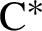 $\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$
-algebras associated with self-similar sets