 $\omega $ WITH WELL-ORDERABLE BASES IN
$\omega $ WITH WELL-ORDERABLE BASES IN  $\mathsf {ZF}$
$\mathsf {ZF}$
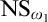 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 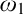 $\omega _1$-Dense” from Large Cardinals
$\omega _1$-Dense” from Large Cardinals
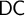 $\mathsf {DC}$ IMPLY
$\mathsf {DC}$ IMPLY 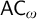 ${\mathsf {AC}}_\omega $, UNIFORMLY?
${\mathsf {AC}}_\omega $, UNIFORMLY?
 ${\mathrm {TD}}$ AND
${\mathrm {TD}}$ AND 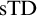 ${\mathrm {sTD}}$
${\mathrm {sTD}}$
 $\mathsf {ZF}$
$\mathsf {ZF}$