Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-28T12:02:59.917Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME CONSEQUENCES OF ${\mathrm {TD}}$ AND 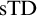${\mathrm {sTD}}$

Part of: Classical measure theory Theory of computing Computability and recursion theory Set theory

Published online by Cambridge University Press:  15 May 2023

YINHE PENG ,
LIUZHEN WU  and
LIANG YU
YINHE PENG
Affiliation:
ACADEMY OF MATHEMATICS AND SYSTEMS SCIENCE CHINESE ACADEMY OF SCIENCES EAST ZHONG GUAN CUN ROAD NO. 55 BEIJING 100190, CHINA E-mail: [email protected]
LIUZHEN WU
Affiliation:
HLM, ACADEMY OF MATHEMATICS AND SYSTEMS SCIENCE CHINESE ACADEMY OF SCIENCES EAST ZHONG GUAN CUN ROAD NO. 55 BEIJING 100190, CHINA E-mail: [email protected]
LIANG YU*
Affiliation:
DEPARTMENT OF MATHEMATICS NANJING UNIVERSITY NANJING, JIANGSU 210093 PEOPLE’S REPUBLIC OF CHINA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Strong Turing Determinacy, or ${\mathrm {sTD}}$, is the statement that for every set A of reals, if 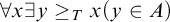$\forall x\exists y\geq _T x (y\in A)$, then there is a pointed set 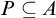$P\subseteq A$. We prove the following consequences of Turing Determinacy (${\mathrm {TD}}$) and ${\mathrm {sTD}}$ over 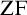${\mathrm {ZF}}$—the Zermelo–Fraenkel axiomatic set theory without the Axiom of Choice:

  1. (1) 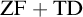${\mathrm {ZF}}+{\mathrm {TD}}$ implies 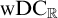$\mathrm {wDC}_{\mathbb {R}}$—a weaker version of 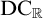$\mathrm {DC}_{\mathbb {R}}$.

  2. (2) 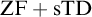${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every set of reals is measurable and has Baire property.

  3. (3) 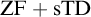${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every uncountable set of reals has a perfect subset.

  4. (4) 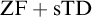${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that for every set of reals A and every 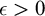$\epsilon>0$:

    1. (a) There is a closed set 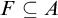$F\subseteq A$ such that 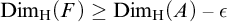$\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)-\epsilon $, where 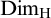$\mathrm {Dim_H}$ is the Hausdorff dimension.

    2. (b) There is a closed set 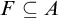$F\subseteq A$ such that 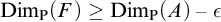$\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)-\epsilon $, where 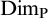$\mathrm {Dim_P}$ is the packing dimension.

Keywords

Axiom of DeterminacyTuring DeterminacyTuring degreesHausdorff dimension

MSC classification

Primary: 03D28: Other Turing degree structures 03E05: Other combinatorial set theory 03E15: Descriptive set theory 03E25: Axiom of choice and related propositions 03E60: Determinacy principles
Secondary: 28A80: Fractals 68Q30: Algorithmic information theory (Kolmogorov complexity, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 4 , December 2023 , pp. 1573 - 1589
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Besicovitch, A. S., On existence of subsets of finite measure of sets of infinite measure . Nederlandse Akademie van Wetenschappen. Proceedings. Series A. Indagationes Mathematicae, vol. 14 (1952), pp. 339–344.Google Scholar
Chong, C. T. and Yu, L., Recursion Theory, De Gruyter Series in Logic and Its Applications, vol. 8, De Gruyter, Berlin, 2015.CrossRefGoogle Scholar
Crone, L., Fishman, L. and Jackson, S. C., Hausdorff dimension regularity properties and games . Israel Journal of Mathematics, vol. 248 (2022), no. 1, pp. 481–500.CrossRefGoogle Scholar
Cutler, C. D., Strong and weak duality principles for fractal dimension in Euclidean space . Mathematical Proceedings of the Cambridge Philosophical Society, vol. 118 (1995), no. 3, pp. 393–410.CrossRefGoogle Scholar
Davies, R. O., Subsets of finite measure in analytic sets . Nederlandse Akademie van Wetenschappen. Proceedings. Series A. Indagationes Mathematicae, vol. 14 (1952), pp. 488–489.Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Falconer, K. J., Fractal Geometry, third ed., Wiley, Chichester, 2014.Google Scholar
Hamel, C., Horowitz, H., and Shelah, S., Turing invariant sets and the perfect set property . Mathematical Logic Quarterly, vol. 66 (2020), no. 2, pp. 247–250.Google Scholar
Herbert, I., A perfect set of reals with finite self-information, Journal of Symbolic Logic, vol. 78 (2013), no. 4, pp. 1229–1246.Google Scholar
Jech, T. J., Set Theory, The third millennium edition, revised and expanded, Springer, Berlin, 2003.Google Scholar
Joyce, H. J. and Preiss, D., On the existence of subsets of finite positive packing measure . Mathematika, vol. 42 (1995), no. 1, pp. 15–24.Google Scholar
Kechris, A. S., The axiom of determinacy implies dependent choices in $L({\mathbf{R}})$ , Journal of Symbolic Logic, vol. 49 (1984), no. 1, pp. 161–173.Google Scholar
Lempp, S., Miller, J. S., Ng, K. M., Turetsky, D. D., and Weber, R., Lowness for effective Hausdorff dimension . Journal of Mathematical Logic, vol. 14 (2014), no. 2, Article no. 1450011.Google Scholar
Lerman, M., Degrees of Unsolvability, Perspectives in Mathematical Logic, vol. 11, Springer, Berlin, 1983.Google Scholar
Lutz, J. H. and Lutz, N., Algorithmic information, plane Kakeya sets, and conditional dimension . ACM Transactions on Computation Theory, vol. 10 (2018), no. 2, Article no. 7, 22 pp.Google Scholar
Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy . Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.CrossRefGoogle Scholar
Moore, J. T., A five element basis for the uncountable linear orders . Annals of Mathematics. Second Series, vol. 163 (2006), no. 2, pp. 669–688.Google Scholar
Mycielski, J., On the axiom of determinateness. Fundamenta Mathematicae, vol. 53 (1963/64), pp. 205–224.Google Scholar
Nies, A. O., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.Google Scholar
Peng, Y. and Yu, L., TD implies CC ${}_{\mathbb{R}}$ . Advances in Mathematics, vol. 384 (2021), Paper no. 107755, 7 pp.Google Scholar
Sacks, G. E., Measure-theoretic uniformity in recursion theory and set theory . Transactions of the American Mathematical Society, vol. 142 (1969), pp. 381–420.Google Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer, Berlin, 1990.CrossRefGoogle Scholar
Sami, R. L., Turing determinacy and the continuum hypothesis . Archive for Mathematical Logic, vol. 28 (1989), no. 3, pp. 149–154.Google Scholar
Schindler, R., Set Theory, Universitext, Springer, Cham, 2014.CrossRefGoogle Scholar
Slaman, T. A., On capacitability for co-analytic sets . New Zealand Journal of Mathematics, vol. 52 (2021), pp. 865–869.Google Scholar
Solovay, R. M., The independence of DC from AD , Cabal Seminar 76–77 (Proceedings, Caltech-UCLA Logic Seminar 1976–1977) (Kechris, A. S. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 689, Springer, Berlin, 1978, pp. 171–183.Google Scholar
Terwijn, S. A. and Zambella, D., Computational randomness and lowness, Journal of Symbolic Logic, vol. 66 (2001), no. 3, pp. 1199–1205.Google Scholar
Woodin, W. H., Turing determinacy and Suslin sets . New Zealand Journal of Mathematics, vol. 52 (2021), pp. 845–863.Google Scholar