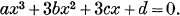
Multiply throughout by a2 and write y for ax+ b ; the equation becomes 
where H ≡ac − b2, G ≡ a2d − 3abc + 2b3.
Since in an equation with real coefficients complex roots occur in conjugate pairs, (i) must have at least one real root; so if α is this root, (i) may be written 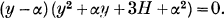
Accordingly the two remaining roots are also real if 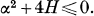
But since α satisfies (i), 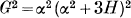
and so 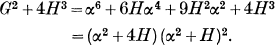
Hence if (i) has three real roots, G2 +4H3 ≤ 0; and clearly, when G2+4H3 = 0, two roots are numerically equal to 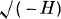 and the third to
and the third to 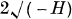 .
.