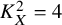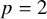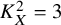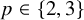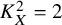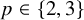1 Introduction
We work over an algebraically closed field of characteristic
![]() $p>0$
. Fano varieties play a significant role in the classification of algebraic varieties. In positive characteristic, properties defined by the Frobenius morphism such as (global) F-splitting or global F-regularity are useful. Therefore, it is natural to ask when Fano varieties are F-split or globally F-regular. For smooth del Pezzo surfaces, Hara [Reference HaraHar98a] proved the following result:
$p>0$
. Fano varieties play a significant role in the classification of algebraic varieties. In positive characteristic, properties defined by the Frobenius morphism such as (global) F-splitting or global F-regularity are useful. Therefore, it is natural to ask when Fano varieties are F-split or globally F-regular. For smooth del Pezzo surfaces, Hara [Reference HaraHar98a] proved the following result:
Theorem 1.1 [Reference HaraHar98a, Example 5.5].
Let X be a smooth del Pezzo surface over an algebraically closed field of characteristic
![]() $p>0$
. Then X is globally F-regular except for the following cases:
$p>0$
. Then X is globally F-regular except for the following cases:
-
(1)
 $K_X^2=3$
and
$K_X^2=3$
and
 $p=2$
.
$p=2$
. -
(2)
 $K_X^2=2$
and
$K_X^2=2$
and
 $p \in \{2, 3\}$
.
$p \in \{2, 3\}$
. -
(3)
 $K_X^2=1$
and
$K_X^2=1$
and
 $p \in \{2, 3, 5\}$
.
$p \in \{2, 3, 5\}$
.
Our aim is to generalize Hara’s result to the case when
![]() $-K_X$
is nef and big, or equivalently, X is canonical. Here, we say that a variety is canonical if it has only canonical singularities. In fact, the following theorem holds.
$-K_X$
is nef and big, or equivalently, X is canonical. Here, we say that a variety is canonical if it has only canonical singularities. In fact, the following theorem holds.
Theorem A. Let k be an algebraically closed field of characteristic
![]() $p>0$
. Let X be a canonical projective surface over k whose anticanonical divisor is nef and big. Then X is globally F-regular except for the following cases:
$p>0$
. Let X be a canonical projective surface over k whose anticanonical divisor is nef and big. Then X is globally F-regular except for the following cases:
-
(1)
 $K_X^2=4$
and
$K_X^2=4$
and
 $p=2$
.
$p=2$
. -
(2)
 $K_X^2=3$
and
$K_X^2=3$
and
 $p \in \{2, 3\}$
.
$p \in \{2, 3\}$
. -
(3)
 $K_X^2=2$
and
$K_X^2=2$
and
 $p \in \{2, 3\}$
.
$p \in \{2, 3\}$
. -
(4)
 $K_X^2=1$
and
$K_X^2=1$
and
 $p \in \{2, 3, 5\}$
.
$p \in \{2, 3, 5\}$
.
Theorem A has an important role for investigating of global F-regularity of smooth Fano threefolds and smooth del Pezzo varieties (see [Reference Kawakami and TanakaKT24b, Reference Kawakami and TanakaKT24c] for details).
Remark 1.2. For each degree
![]() $K_X^2$
, the assumption on p is optimal. In fact, for each case listed above, there exists a canonical del Pezzo surface that is not strongly F-regular (see [Reference Kawakami and NagaokaKN23, Table 1] and [Reference Kawakami and TakamatsuKT24a, Table 1]).
$K_X^2$
, the assumption on p is optimal. In fact, for each case listed above, there exists a canonical del Pezzo surface that is not strongly F-regular (see [Reference Kawakami and NagaokaKN23, Table 1] and [Reference Kawakami and TakamatsuKT24a, Table 1]).
The assumption on p is still optimal even if we assume that X is smooth since taking the minimal resolution does not change the degree and globally F-regularity (Corollary 2.5). Similarly, even if we replace ‘nef and big’ by ‘ample’, the conclusion of Theorem A is the same. This is because X is globally F-regular if and only if its anticanonical model is globally F-regular (Proposition 2.4). In particular, Theorem A does not imply Theorem 1.1.
Remark 1.3. For each prime number p, there exists a Kawamata log terminal (klt) del Pezzo surface X (i.e., a normal projective surface such that
![]() $(X, 0)$
is klt and
$(X, 0)$
is klt and
![]() $-K_X$
is ample) that is not F-split [Reference Cascini, Tanaka H and WitaszekCTW18, Theorem 1.1].
$-K_X$
is ample) that is not F-split [Reference Cascini, Tanaka H and WitaszekCTW18, Theorem 1.1].
We now focus on the proof of Theorem A. We first investigate when X as in Theorem A is F-split. The proof is divided into two cases: the case where
![]() $K_X^2\geq 5$
and the case where
$K_X^2\geq 5$
and the case where
![]() $K_X^2\leq 4$
.
$K_X^2\leq 4$
.
First, we consider the case where
![]() $K_X^2\geq 5$
. We may assume that X is obtained by taking a blowup
$K_X^2\geq 5$
. We may assume that X is obtained by taking a blowup
![]() $f\colon X \to {\mathbb {P}}^2$
along some points. Recall that if there exists an effective divisor
$f\colon X \to {\mathbb {P}}^2$
along some points. Recall that if there exists an effective divisor
![]() $\Delta _{{\mathbb {P}}^2}$
on
$\Delta _{{\mathbb {P}}^2}$
on
![]() ${\mathbb {P}}^2$
such that the divisor
${\mathbb {P}}^2$
such that the divisor
![]() $\Delta $
on X defined by
$\Delta $
on X defined by
![]() $K_X+\Delta = f^*(K_{{\mathbb {P}}^2}+\Delta _{{\mathbb {P}}^2})$
is effective, then the following holds (Proposition 2.4):
$K_X+\Delta = f^*(K_{{\mathbb {P}}^2}+\Delta _{{\mathbb {P}}^2})$
is effective, then the following holds (Proposition 2.4):
Such a divisor
![]() $\Delta _{{\mathbb {P}}^2}$
can be found by utilizing an inversion of adjunction for F-splitting (Proposition 2.6). However, since we can only assume that the blowup points are in almost general position, the situation is more complicated than the smooth del Pezzo cases, which are obtained by blowing up points in general position. For more details, see Proposition 3.8.
$\Delta _{{\mathbb {P}}^2}$
can be found by utilizing an inversion of adjunction for F-splitting (Proposition 2.6). However, since we can only assume that the blowup points are in almost general position, the situation is more complicated than the smooth del Pezzo cases, which are obtained by blowing up points in general position. For more details, see Proposition 3.8.
Next, we consider the case where
![]() $K_X^2\leq 4$
. In the case of smooth del Pezzo surfaces, Hara [Reference HaraHar98a] investigated F-splitting using the following two steps:
$K_X^2\leq 4$
. In the case of smooth del Pezzo surfaces, Hara [Reference HaraHar98a] investigated F-splitting using the following two steps:
-
(i) The reduction of F-splitting to the vanishing
 $H^1(X, \Omega _X^{1}(pK_X))=0$
via the Cartier operator.
$H^1(X, \Omega _X^{1}(pK_X))=0$
via the Cartier operator. -
(ii) Embedding X as a hypersurface or a complete intersection of a weighted projective space and proving the vanishing
 $H^1(X, \Omega _X^{1}(pK_X))=0$
.
$H^1(X, \Omega _X^{1}(pK_X))=0$
.
For a smooth weak del Pezzo surface X, we can also reduce the F-splitting of X to the vanishing
![]() $H^1(X, \Omega _X^{1}(pK_X))=0$
. However, Step (ii), proving
$H^1(X, \Omega _X^{1}(pK_X))=0$
. However, Step (ii), proving
![]() $H^1(X, \Omega _X^{1}(pK_X))=0$
, is not easy because X is not embedded in a weighted projective space via
$H^1(X, \Omega _X^{1}(pK_X))=0$
, is not easy because X is not embedded in a weighted projective space via
![]() $|-mK_X|$
for
$|-mK_X|$
for
![]() $m\in \mathbb {Z}_{>0}$
. Therefore, by replacing X with its anticanonical model, we embed X into a weighted projective space via
$m\in \mathbb {Z}_{>0}$
. Therefore, by replacing X with its anticanonical model, we embed X into a weighted projective space via
![]() $|-mK_X|$
. However, in this case, Step (i), the reduction of the F-splitting of X to the vanishing
$|-mK_X|$
. However, in this case, Step (i), the reduction of the F-splitting of X to the vanishing
![]() $H^1(X, \Omega _X^{1}(pK_X))=0$
, is not straightforward since Cartier operator is defined on smooth schemes. To address this issue, we use the reflexive Cartier operator introduced in [Reference KawakamiKaw22b]. Indeed, we utilize the fact that the reflexive Cartier operator behaves well on F-pure klt surfaces (Lemma 3.1).
$H^1(X, \Omega _X^{1}(pK_X))=0$
, is not straightforward since Cartier operator is defined on smooth schemes. To address this issue, we use the reflexive Cartier operator introduced in [Reference KawakamiKaw22b]. Indeed, we utilize the fact that the reflexive Cartier operator behaves well on F-pure klt surfaces (Lemma 3.1).
Combining the above results, we obtain the following theorem.
Theorem B. Let k be an algebraically closed field of characteristic
![]() $p>0$
. Let X be a canonical F-pure projective surface over k whose anticanonical divisor is ample. Then X is F-split except for the following cases:
$p>0$
. Let X be a canonical F-pure projective surface over k whose anticanonical divisor is ample. Then X is F-split except for the following cases:
-
(1)
 $K_X^2=3$
and
$K_X^2=3$
and
 $p=2$
.
$p=2$
. -
(2)
 $K_X^2=2$
and
$K_X^2=2$
and
 $p \in \{2, 3\}$
.
$p \in \{2, 3\}$
. -
(3)
 $K_X^2=1$
and
$K_X^2=1$
and
 $p \in \{2, 3, 5\}$
.
$p \in \{2, 3, 5\}$
.
Remark 1.4.
-
(1) When
 $K_X^2=4$
and
$K_X^2=4$
and
 $p=2$
, there exists a a canonical del Pezzo surface with
$p=2$
, there exists a a canonical del Pezzo surface with
 $D^0_5$
-singularity, which is not F-pure [Reference Kawakami and NagaokaKN23, Proposition 3.16].
$D^0_5$
-singularity, which is not F-pure [Reference Kawakami and NagaokaKN23, Proposition 3.16]. -
(2) When
 $K_X^2=3$
and
$K_X^2=3$
and
 $p=3$
, there exists a canonical del Pezzo surface with
$p=3$
, there exists a canonical del Pezzo surface with
 $E^0_6$
-singularity, which is not F-pure [Reference Kawakami and NagaokaKN23, Proposition 3.22].
$E^0_6$
-singularity, which is not F-pure [Reference Kawakami and NagaokaKN23, Proposition 3.22].
Finally, we now overview how to deduce Theorem A from Theorem B. Let X be a canonical weak del Pezzo surface. Replacing X with its anticanonical model, we can assume that
![]() $-K_X$
is ample. For each degree
$-K_X$
is ample. For each degree
![]() $K_X^2$
, we will find an optimal bound on p that ensures all the singularities of X are strongly F-regular (see Lemma 3.9). We then conclude by the following well-known fact that asserts the equivalence between F-splitting and global F-regularity for strongly F-regular
$K_X^2$
, we will find an optimal bound on p that ensures all the singularities of X are strongly F-regular (see Lemma 3.9). We then conclude by the following well-known fact that asserts the equivalence between F-splitting and global F-regularity for strongly F-regular
![]() $\mathbb {Q}$
-Gorenstein Fano varieties:
$\mathbb {Q}$
-Gorenstein Fano varieties:
Theorem 1.5 (cf. [Reference Kawakami and TotaroKT23, Proof of Theorem 6.2]).
Let X be a normal projective variety such that
![]() $-K_X$
is an ample
$-K_X$
is an ample
![]() $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
![]() $\mathbb {Z}$
-divisor. Suppose that X is strongly F-regular. If X is F-split, then X is globally F-regular.
$\mathbb {Z}$
-divisor. Suppose that X is strongly F-regular. If X is F-split, then X is globally F-regular.
2 Preliminaries
2.1 Notation and terminology
In this subsection, we summarize notation and basic definitions used in this article.
-
(1) Throughout the paper, p denotes a prime number and we work over an algebraically closed field k of characteristic
 $p>0$
. We set
$p>0$
. We set  . We denote by
. We denote by
 $F \colon X \to X$
the absolute Frobenius morphism on an
$F \colon X \to X$
the absolute Frobenius morphism on an
 $\mathbb {F}_p$
-scheme X.
$\mathbb {F}_p$
-scheme X. -
(2) We say that X is a variety (over k) if X is an integral scheme that is separated and of finite type over k. We say that X is a curve (resp. surface) if X is a variety of dimension one (resp. two).
-
(3) For a variety X, we define the function field
 $K(X)$
of X as the stalk
$K(X)$
of X as the stalk
 $\mathcal {O}_{X, \xi }$
at the generic point
$\mathcal {O}_{X, \xi }$
at the generic point
 $\xi $
of X.
$\xi $
of X. -
(4) We say that a
 $\mathbb {Q}$
-divisor D on a normal variety X is simple normal crossing if for every point
$\mathbb {Q}$
-divisor D on a normal variety X is simple normal crossing if for every point
 ${x \in \operatorname {\mathrm {Supp}} D}$
, the local ring
${x \in \operatorname {\mathrm {Supp}} D}$
, the local ring
 $\mathcal {O}_{X,x}$
is regular and there exists a regular system of parameters
$\mathcal {O}_{X,x}$
is regular and there exists a regular system of parameters
 $x_1,\ldots , x_d$
of the maximal ideal
$x_1,\ldots , x_d$
of the maximal ideal
 $\mathfrak {m}$
of
$\mathfrak {m}$
of
 $\mathcal {O}_{X,x}$
and
$\mathcal {O}_{X,x}$
and
 $1 \leq r \leq d$
such that
$1 \leq r \leq d$
such that
 $\operatorname {\mathrm {Supp}} (D|_{\operatorname {\mathrm {Spec}} \mathcal {O}_{X, x}}) = \operatorname {\mathrm {Spec}} (\mathcal {O}_{X,x}/(x_1 \cdots x_r))$
.
$\operatorname {\mathrm {Supp}} (D|_{\operatorname {\mathrm {Spec}} \mathcal {O}_{X, x}}) = \operatorname {\mathrm {Spec}} (\mathcal {O}_{X,x}/(x_1 \cdots x_r))$
. -
(5) Given a variety X, a projective birational morphism
 $\pi \colon Y \to X$
is called a log resolution of X if Y is a smooth variety and
$\pi \colon Y \to X$
is called a log resolution of X if Y is a smooth variety and
 $\mathrm {Exc}(f)$
is a simple normal crossing divisor.
$\mathrm {Exc}(f)$
is a simple normal crossing divisor. -
(6) Given a variety X and a closed subscheme Z, we denote by
 $\operatorname {\mathrm {Bl}}_Z X$
the blowup of X along Z.
$\operatorname {\mathrm {Bl}}_Z X$
the blowup of X along Z. -
(7) Given a normal variety X and a
 $\mathbb {Z}$
-divisor D on X, we define a reflexive sheaf
$\mathbb {Z}$
-divisor D on X, we define a reflexive sheaf
 $\Omega _X^{[i]}(D)$
by
$\Omega _X^{[i]}(D)$
by
 $j_{*}(\Omega _U^{i}\otimes \mathcal {O}_U(D))$
, where
$j_{*}(\Omega _U^{i}\otimes \mathcal {O}_U(D))$
, where
 $j\colon U\hookrightarrow X$
is the open immersion from the smooth locus U of X.
$j\colon U\hookrightarrow X$
is the open immersion from the smooth locus U of X.
2.1.1 Singularities in minimal model program
For the definitions of singularities in minimal model program (e.g., canonical and klt), we refer to [Reference Kollár and MoriKM98, Section 2.3]. Take a normal surface X. Let
![]() $f\colon Y \to X$
be the minimal resolution. We only need the following characterizations in this paper.
$f\colon Y \to X$
be the minimal resolution. We only need the following characterizations in this paper.
-
(1) X is canonical if and only if
 $K_X$
is
$K_X$
is
 $\mathbb {Q}$
-Cartier and
$\mathbb {Q}$
-Cartier and
 $K_Y \sim _{\mathbb {Q}} f^*K_X$
.
$K_Y \sim _{\mathbb {Q}} f^*K_X$
. -
(2) X is klt if and only if
 $K_X$
is
$K_X$
is
 $\mathbb {Q}$
-Cartier, f is a log resolution of X and all the coefficients of the
$\mathbb {Q}$
-Cartier, f is a log resolution of X and all the coefficients of the
 $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $\Gamma $
defined by
$\Gamma $
defined by
 $K_Y+\Gamma \sim _{\mathbb {Q}} f^*K_X$
are
$K_Y+\Gamma \sim _{\mathbb {Q}} f^*K_X$
are
 $<1$
.
$<1$
.
By definition, we have
Moreover, the following implications hold for the surface case:
-
• canonical
 $\Rightarrow $
Gorenstein.
$\Rightarrow $
Gorenstein. -
• klt
 $\Rightarrow \mathbb {Q}$
-factorial.
$\Rightarrow \mathbb {Q}$
-factorial.
2.1.2 Weak del Pezzo surfaces
Given a normal projective Gorenstein surface X, we say that X is del Pezzo (resp. weak del Pezzo) if
![]() $-K_X$
is ample (resp. nef and big). In what follows, we summarize some properties on (weak) del Pezzo surfaces for later usage.
$-K_X$
is ample (resp. nef and big). In what follows, we summarize some properties on (weak) del Pezzo surfaces for later usage.
Let Z be a canonical weak del Pezzo surface. The anticanonical model Y of Z is defined as the Stein factorisation of the morphism
![]() $\varphi _{|-mK_Z|} \colon Z \to {\mathbb {P}}^{h^0(Z, -mK_Z)-1}$
induced by the complete linear system
$\varphi _{|-mK_Z|} \colon Z \to {\mathbb {P}}^{h^0(Z, -mK_Z)-1}$
induced by the complete linear system
![]() $|-mK_Z|$
, where m is a positive integer such that
$|-mK_Z|$
, where m is a positive integer such that
![]() $|-mK_X|$
is base point free (whose existence is guaranteed by [Reference TanakaTan15, Theorem 0.4]). Then Y is canonical, because have
$|-mK_X|$
is base point free (whose existence is guaranteed by [Reference TanakaTan15, Theorem 0.4]). Then Y is canonical, because have
![]() $K_Z \sim h^*K_Y$
for the induced morphism
$K_Z \sim h^*K_Y$
for the induced morphism
![]() $h \colon Z \to Y$
. Moreover, h is obtained by contracting all the
$h \colon Z \to Y$
. Moreover, h is obtained by contracting all the
![]() $(-2)$
-curves on Y. In particular, the minimal resolution X of Z coincides with the minimal resolution of Y:
$(-2)$
-curves on Y. In particular, the minimal resolution X of Z coincides with the minimal resolution of Y:
Moreover, X is a smooth weak del Pezzo surface.
There is a natural one-to-one correspondence between
-
• smooth weak del Pezzo surfaces and
-
• canonical del Pezzo surfaces.
Indeed, if Y is a canonical del Pezzo surface, then its minimal resolution X is a smooth weak del Pezzo surface. Conversely, given a smooth weak del Pezzo surface X, its anticanonical model Y is a canonical del Pezzo surface.
2.2 F-splitting and global F–regularity
In this subsection, we gather basic facts on F-splitting and global F-regularity.
Definition 2.1. Let X be a normal variety, and let
![]() $\Delta $
be an effective
$\Delta $
be an effective
![]() $\mathbb {Q}$
-divisor on X.
$\mathbb {Q}$
-divisor on X.
-
(1) We say that
 $(X, \Delta )$
is F-split if splits as an
$(X, \Delta )$
is F-split if splits as an $$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lfloor(p^e-1)\Delta \rfloor) \end{align*}$$
$$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lfloor(p^e-1)\Delta \rfloor) \end{align*}$$
 $\mathcal {O}_X$
-module homomorphism for every
$\mathcal {O}_X$
-module homomorphism for every
 $e \in \mathbb {Z}_{>0}$
.
$e \in \mathbb {Z}_{>0}$
.
-
(2) We say that
 $(X, \Delta )$
is sharply F-split if splits as an
$(X, \Delta )$
is sharply F-split if splits as an $$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lceil(p^e-1)\Delta \rceil) \end{align*}$$
$$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lceil(p^e-1)\Delta \rceil) \end{align*}$$
 $\mathcal {O}_X$
-module homomorphism for some
$\mathcal {O}_X$
-module homomorphism for some
 $e \in \mathbb {Z}_{>0}$
.
$e \in \mathbb {Z}_{>0}$
.
-
(3) We say that
 $(X, \Delta )$
is globally F-regular if, given an effective
$(X, \Delta )$
is globally F-regular if, given an effective
 $\mathbb {Z}$
-divisor E, there exists
$\mathbb {Z}$
-divisor E, there exists
 $e \in \mathbb {Z}_{>0}$
such that splits as an
$e \in \mathbb {Z}_{>0}$
such that splits as an $$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lceil(p^e-1)\Delta \rceil +E) \end{align*}$$
$$\begin{align*}\mathcal{O}_X \xrightarrow{F^e} F_*^e\mathcal{O}_X \hookrightarrow F_*^e\mathcal{O}_X( \lceil(p^e-1)\Delta \rceil +E) \end{align*}$$
 $\mathcal {O}_X$
-module homomorphism.
$\mathcal {O}_X$
-module homomorphism.
We say that X is F-split (resp. globally F-regular) if so is
![]() $(X, 0)$
.
$(X, 0)$
.
Remark 2.2. We have the following implications:
where the former implication is easy and the latter one holds by the same argument as in [Reference SchwedeSch08, Proposition 3.3]. Moreover, if the condition (
![]() $\star $
) holds, then
$\star $
) holds, then
![]() $(X, \Delta )$
is sharply F-split if and only if
$(X, \Delta )$
is sharply F-split if and only if
![]() $(X, \Delta )$
is F-split.
$(X, \Delta )$
is F-split.
-
(⋆)
 $(p^e-1)\Delta $
is a
$(p^e-1)\Delta $
is a
 $\mathbb {Z}$
-divisor for some
$\mathbb {Z}$
-divisor for some
 $e \in \mathbb {Z}_{>0}$
.
$e \in \mathbb {Z}_{>0}$
.
In particular, X is F-split if and only if
![]() $F\colon \mathcal {O}_X \to F_*\mathcal {O}_X$
splits as an
$F\colon \mathcal {O}_X \to F_*\mathcal {O}_X$
splits as an
![]() $\mathcal {O}_X$
-module homomorphism. In this paper, we only treat the case when (
$\mathcal {O}_X$
-module homomorphism. In this paper, we only treat the case when (
![]() $\star $
) holds, and hence being F-split is equivalent to being sharply F-split. For more foundational properties, we refer to [Reference Schwede and SmithSS10].
$\star $
) holds, and hence being F-split is equivalent to being sharply F-split. For more foundational properties, we refer to [Reference Schwede and SmithSS10].
We shall also use the local versions of F-splitting and global F-regularity.
Definition 2.3. Given a normal variety X, we say that X is F-pure (resp. strongly F-regular) if there exists an open cover
![]() $X = \bigcup _{i \in I} X_i$
such that
$X = \bigcup _{i \in I} X_i$
such that
![]() $X_i$
is F-split (resp. globally F-regular) for every
$X_i$
is F-split (resp. globally F-regular) for every
![]() $i \in I$
.
$i \in I$
.
In what follows, we summarize some F-splitting criteria, which are well known to experts.
Proposition 2.4. Let
![]() $f: X \to Y$
be a birational morphism of normal projective varieties. Take an effective
$f: X \to Y$
be a birational morphism of normal projective varieties. Take an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $\Delta _Y$
on Y such that
$\Delta _Y$
on Y such that
![]() $(p^e-1)(K_Y+\Delta _Y)$
is Cartier for some
$(p^e-1)(K_Y+\Delta _Y)$
is Cartier for some
![]() $e \in \mathbb {Z}_{>0}$
. Assume that the
$e \in \mathbb {Z}_{>0}$
. Assume that the
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $\Delta $
defined by
$\Delta $
defined by
![]() $K_X+\Delta = f^*(K_Y+\Delta _Y)$
is effective. Then
$K_X+\Delta = f^*(K_Y+\Delta _Y)$
is effective. Then
![]() $(X, \Delta )$
is F-split (resp. globally F-regular) if and only if
$(X, \Delta )$
is F-split (resp. globally F-regular) if and only if
![]() $(Y, \Delta _Y)$
is F-split (resp. globally F-regular).
$(Y, \Delta _Y)$
is F-split (resp. globally F-regular).
Proof. If
![]() $(X, \Delta )$
is F-split, then so is
$(X, \Delta )$
is F-split, then so is
![]() $(Y, \Delta _Y)$
, which can be checked by taking the push-forward. As for the opposite implication, the same argument as in the first paragraph of the proof of [Reference Xu ChenyangHX15, Proposition 2.11] works.
$(Y, \Delta _Y)$
, which can be checked by taking the push-forward. As for the opposite implication, the same argument as in the first paragraph of the proof of [Reference Xu ChenyangHX15, Proposition 2.11] works.
Corollary 2.5. Let Y be a canonical projective surface, and let
![]() $f: X \to Y$
be its minimal resolution. Then X is F-split (resp. globally F-regular) if and only if Y is F-split (resp. globally F-regular).
$f: X \to Y$
be its minimal resolution. Then X is F-split (resp. globally F-regular) if and only if Y is F-split (resp. globally F-regular).
Proof. The assertion immediately follows from Proposition 2.4 by using
![]() $K_X =f^*K_Y$
.
$K_X =f^*K_Y$
.
Proposition 2.6. Let X be a normal projective Gorenstein variety. Take a normal prime Cartier divisor S and an effective
![]() $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
![]() $\mathbb {Q}$
-divisor B on X such that
$\mathbb {Q}$
-divisor B on X such that
![]() $S \not \subset \operatorname {\mathrm {Supp}}\,B$
. Assume that
$S \not \subset \operatorname {\mathrm {Supp}}\,B$
. Assume that
-
(1)
 $(S, B|_S)$
is F-split, and
$(S, B|_S)$
is F-split, and -
(2) there is a positive integer
 $e \in \mathbb {Z}_{>0}$
such that
$e \in \mathbb {Z}_{>0}$
such that
 $(p^e-1)(K_X+S+B)$
is Cartier and
$(p^e-1)(K_X+S+B)$
is Cartier and  $$\begin{align*}H^1(X, \mathcal{O}_X(-S-(p^e-1)(K_X+S+B)))=0. \end{align*}$$
$$\begin{align*}H^1(X, \mathcal{O}_X(-S-(p^e-1)(K_X+S+B)))=0. \end{align*}$$
Then
![]() $(X, S+B)$
is F-split.
$(X, S+B)$
is F-split.
Proof. The same argument as in [Reference Cascini, Tanaka and WitaszekCTW17, Lemma 2.7] works.
Example 2.7. We now summarize some easy cases for later usage, although all of them are well known to experts,
-
(1) If
 $P, Q \in {\mathbb {P}}^1$
are distinct points, then
$P, Q \in {\mathbb {P}}^1$
are distinct points, then
 $({\mathbb {P}}^1, P+Q)$
is F-split (Proposition 2.6).
$({\mathbb {P}}^1, P+Q)$
is F-split (Proposition 2.6). -
(2) Let
 $L, L', L"$
be three lines on
$L, L', L"$
be three lines on
 ${\mathbb {P}}^2$
such that
${\mathbb {P}}^2$
such that
 $L+L'+L"$
is simple normal crossing. Then
$L+L'+L"$
is simple normal crossing. Then
 $({\mathbb {P}}^2, L+L'+L")$
is F-split by (1) and Proposition 2.6.
$({\mathbb {P}}^2, L+L'+L")$
is F-split by (1) and Proposition 2.6. -
(3) For each
 $i \in \{1, 2\}$
, let
$i \in \{1, 2\}$
, let
 $F_i$
and
$F_i$
and
 $F^{\prime }_i$
be distinct fibers of the i-th projection
$F^{\prime }_i$
be distinct fibers of the i-th projection
 $\mathrm {pr}_i \colon {\mathbb {P}}^1 \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$
. Then
$\mathrm {pr}_i \colon {\mathbb {P}}^1 \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$
. Then
 $({\mathbb {P}}^1 \times {\mathbb {P}}^1, F_1 +F^{\prime }_1 + F_2+F^{\prime }_2)$
is F-split by (1) and Proposition 2.6.
$({\mathbb {P}}^1 \times {\mathbb {P}}^1, F_1 +F^{\prime }_1 + F_2+F^{\prime }_2)$
is F-split by (1) and Proposition 2.6.
2.3 Reflexive Cartier operator
Throughout this subsection, we use the following convention unless stated otherwise.
Convention 2.8. Let X be a normal variety and D a
![]() $\mathbb {Z}$
-divisor on X. Let U be the smooth locus of X and
$\mathbb {Z}$
-divisor on X. Let U be the smooth locus of X and
![]() $j\colon U\hookrightarrow X$
the inclusion. By abuse of notation,
$j\colon U\hookrightarrow X$
the inclusion. By abuse of notation,
![]() $D|_U$
is denoted by D.
$D|_U$
is denoted by D.
The Frobenius pushforward of the de Rham complex
is a complex of
![]() $\mathcal {O}_U$
-modules. Tensoring with
$\mathcal {O}_U$
-modules. Tensoring with
![]() $\mathcal {O}_U(D)$
, we obtain a complex
$\mathcal {O}_U(D)$
, we obtain a complex
We define coherent
![]() $\mathcal {O}_U$
-modules
$\mathcal {O}_U$
-modules
![]() $B^{i}_U(pD)$
and
$B^{i}_U(pD)$
and
![]() $Z^{i}_U(pD)$
by
$Z^{i}_U(pD)$
by

for all
![]() $i\geq 0$
. Then
$i\geq 0$
. Then
![]() $B^{i}_U(pD)$
and
$B^{i}_U(pD)$
and
![]() $Z^{i}_U(pD)$
are locally free [Reference KawakamiKaw22b, Lemma 3.2]. When
$Z^{i}_U(pD)$
are locally free [Reference KawakamiKaw22b, Lemma 3.2]. When
![]() $D=0$
, we simply denote
$D=0$
, we simply denote
![]() $B^{i}_U(pD)$
and
$B^{i}_U(pD)$
and
![]() $Z^{i}_U(pD)$
by
$Z^{i}_U(pD)$
by
![]() $B^{i}_U$
and
$B^{i}_U$
and
![]() $Z^{i}_U$
, respectively. Then
$Z^{i}_U$
, respectively. Then
![]() $B^{i}_U(pD)=B^{i}_U\otimes \mathcal {O}_U(D)$
and
$B^{i}_U(pD)=B^{i}_U\otimes \mathcal {O}_U(D)$
and
![]() $Z^{i}_U(pD)=Z^{i}_U\otimes \mathcal {O}_U(D)$
holds [Reference KawakamiKaw22b, Remark 3.3]. In particular, we note that
$Z^{i}_U(pD)=Z^{i}_U\otimes \mathcal {O}_U(D)$
holds [Reference KawakamiKaw22b, Remark 3.3]. In particular, we note that
![]() $B^{i}_U(pD)$
and
$B^{i}_U(pD)$
and
![]() $Z^{i}_U(pD)$
do not mean
$Z^{i}_U(pD)$
do not mean
![]() $B^{i}_U\otimes \mathcal {O}_U(pD)$
and
$B^{i}_U\otimes \mathcal {O}_U(pD)$
and
![]() $Z^{i}_U\otimes \mathcal {O}_U(pD)$
.
$Z^{i}_U\otimes \mathcal {O}_U(pD)$
.
By [Reference KawakamiKaw22b, Lemma 3.2], there exists an exact sequence
and the map
![]() $C^{i}_{U}(D)$
coincides with
$C^{i}_{U}(D)$
coincides with
![]() $C^{i}_{U}\otimes \mathcal {O}_U(D)$
, where
$C^{i}_{U}\otimes \mathcal {O}_U(D)$
, where
![]() $C^{i}_{U}$
is the usual Cartier operator.
$C^{i}_{U}$
is the usual Cartier operator.
Definition 2.9. We define reflexive
![]() $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
![]() $B^{[i]}_X(pD)$
and
$B^{[i]}_X(pD)$
and
![]() $Z^{[i]}_X(pD)$
by
$Z^{[i]}_X(pD)$
by

for all
![]() $i\geq 0$
. The i-th reflexive Cartier operator
$i\geq 0$
. The i-th reflexive Cartier operator
associated to D is defined as
![]() $j_{*}C^{i}_{U}(D)$
for all
$j_{*}C^{i}_{U}(D)$
for all
![]() $i\geq 0$
.
$i\geq 0$
.
Lemma 2.10. There exist the following exact sequences:
for all
![]() $i\geq 0$
. Moreover,
$i\geq 0$
. Moreover,
![]() $d'|_U \colon F_{*}\Omega ^{[i]}_X(pD)|_U \to B^{[i+1]}_X(pD)|_U$
and
$d'|_U \colon F_{*}\Omega ^{[i]}_X(pD)|_U \to B^{[i+1]}_X(pD)|_U$
and
![]() $C^{[i]}_{X}(D)|_U \colon Z^{[i]}_X(pD)|_U \to \Omega ^{[i]}_X(D)|_U$
are surjective, and the homomorphism
$C^{[i]}_{X}(D)|_U \colon Z^{[i]}_X(pD)|_U \to \Omega ^{[i]}_X(D)|_U$
are surjective, and the homomorphism
![]() $C^{[i]}_{X}(D)|_{U}$
coincides with
$C^{[i]}_{X}(D)|_{U}$
coincides with
![]() $C^{i}_{U}\otimes \mathcal {O}_U(D)$
.
$C^{i}_{U}\otimes \mathcal {O}_U(D)$
.
Proof. Taking
![]() $B=0$
in [Reference KawakamiKaw22b, Lemma 3.5], we obtain the assertion.
$B=0$
in [Reference KawakamiKaw22b, Lemma 3.5], we obtain the assertion.
Remark 2.11. Taking
![]() $i=0$
in equation (2.10.1), we obtain an exact sequence
$i=0$
in equation (2.10.1), we obtain an exact sequence
and the first map is induced by the Frobenius homomorphism. In particular,
holds.
3 Proofs of main theorems
3.1 Criterion of the F-splitting of klt surfaces
In this subsection, we provide a criterion for the F-splitting of klt surfaces (Proposition 3.2).
Lemma 3.1. Let X be an F-pure klt surface and D a
![]() $\mathbb {Z}$
-divisor. Then the sequence
$\mathbb {Z}$
-divisor. Then the sequence
is exact.
Proof. It is enough to show that
![]() $C_X^{[1]}(D)$
is surjective, as the other parts has been settled in Lemma 2.10. Since the assertion is local on X, we may assume that X is affine and has a unique singular point Q. If
$C_X^{[1]}(D)$
is surjective, as the other parts has been settled in Lemma 2.10. Since the assertion is local on X, we may assume that X is affine and has a unique singular point Q. If
![]() $p\neq 5$
or the singularity Q is not rational double point (RDP) of type
$p\neq 5$
or the singularity Q is not rational double point (RDP) of type
![]() $E_8^1$
, then X is F-liftable by [Reference Kawakami and TakamatsuKT24a, Theorem A]. Then the surjectivity of
$E_8^1$
, then X is F-liftable by [Reference Kawakami and TakamatsuKT24a, Theorem A]. Then the surjectivity of
![]() $C^{[1]}(D)$
follows from [Reference KawakamiKaw22b, Lemma 3.8].
$C^{[1]}(D)$
follows from [Reference KawakamiKaw22b, Lemma 3.8].
Suppose that
![]() $p=5$
and the singularity Q is of type
$p=5$
and the singularity Q is of type
![]() $E_8^1$
. Then we may assume that
$E_8^1$
. Then we may assume that
![]() $D=0$
by [Reference LipmanLip69, Section 24] (see also [Reference Liedtke, Martin and MatsumotoLMM21, Table 2]). Then the desired surjectivity follows from [Reference KawakamiKaw22b, Proposition 4.4] and [Reference Kawakami and TakamatsuKT24a, Theorem B].
$D=0$
by [Reference LipmanLip69, Section 24] (see also [Reference Liedtke, Martin and MatsumotoLMM21, Table 2]). Then the desired surjectivity follows from [Reference KawakamiKaw22b, Proposition 4.4] and [Reference Kawakami and TakamatsuKT24a, Theorem B].
Proposition 3.2. Let X be an F-pure klt projective surface. Suppose that the following conditions hold:
-
(1)
 $H^0(X, \Omega _X^{[1]}(K_X))=0$
.
$H^0(X, \Omega _X^{[1]}(K_X))=0$
. -
(2)
 $H^1(X, \Omega _X^{[1]}(pK_X))=0$
.
$H^1(X, \Omega _X^{[1]}(pK_X))=0$
. -
(3)
 $H^0(X, \mathcal {O}_X((p+1)K_X))=0$
.
$H^0(X, \mathcal {O}_X((p+1)K_X))=0$
.
Then X is F-split.
Proof. Recall that X is F-split if and only if the evaluation map
is surjective. Then, as in [Reference Brion and KumarBK05, 1.3.9 Remarks (ii)], the surjectivity is equivalent to the injectivity of the map
induced by Frobenius by Serre duality. Let U be the smooth locus of X. Since U is F-pure, the exact sequence
splits locally by definition. Tensoring with
![]() $\mathcal {O}_U(K_X)$
, we obtain a locally split exact sequence
$\mathcal {O}_U(K_X)$
, we obtain a locally split exact sequence
Since the above exact sequence splits locally, taking pushforward preserves exactness on the right. Thus, taking the pushforward by the inclusion
![]() $U\hookrightarrow X$
, we obtain the following locally split exact sequence
$U\hookrightarrow X$
, we obtain the following locally split exact sequence
Therefore, for the injectivity of equation (3.2.1), it suffices to show that
![]() $H^1(X, B^{[1]}_X(pK_X))=0$
. By Lemma 3.1 and the condition (1), it is enough to prove that
$H^1(X, B^{[1]}_X(pK_X))=0$
. By Lemma 3.1 and the condition (1), it is enough to prove that
![]() $H^1(X, Z_X^{[1]}(pK_X))=0$
. By equation (2.10.1), we have an exact sequence
$H^1(X, Z_X^{[1]}(pK_X))=0$
. By equation (2.10.1), we have an exact sequence
Let ![]() . Then we obtain an exact sequence
. Then we obtain an exact sequence
Since we have
we conclude that
![]() $H^1(X, Z_X^{[1]}(pK_X))=0$
.
$H^1(X, Z_X^{[1]}(pK_X))=0$
.
The condition (3) of Proposition 3.2 is satisfied if
![]() $-K_X$
is big. In what follows, we see when the condition (1) of Proposition 3.2 is satisfied.
$-K_X$
is big. In what follows, we see when the condition (1) of Proposition 3.2 is satisfied.
Definition 3.3 (Log liftability).
Let X be a normal projective surface. We say that X is log liftable if there exists a log resolution
![]() $f\colon Y \to X$
of X such that
$f\colon Y \to X$
of X such that
![]() $(Y,\mathrm {Exc}(f))$
lifts to the ring
$(Y,\mathrm {Exc}(f))$
lifts to the ring
![]() $W(k)$
of Witt vectors. For the definition of liftability of a log smooth pair, we refer to [Reference KawakamiKaw22a, Definition 2.6].
$W(k)$
of Witt vectors. For the definition of liftability of a log smooth pair, we refer to [Reference KawakamiKaw22a, Definition 2.6].
Lemma 3.4. Let X be a normal projective F-pure surface such that
![]() $-K_X$
is a nef and big
$-K_X$
is a nef and big
![]() $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
![]() $\mathbb {Z}$
-divisor. Then X is log liftable if and only if
$\mathbb {Z}$
-divisor. Then X is log liftable if and only if
![]() $H^0(X, \Omega _X^{[1]}(K_X))=0$
.
$H^0(X, \Omega _X^{[1]}(K_X))=0$
.
Proof. Since
![]() $H^2(X, \mathcal {O}_X)\cong H^0(X, \mathcal {O}_X(K_X))=0$
, the ‘if’ direction is [Reference KawakamiKaw22c, Theorem 2.8]. We prove the ‘only if’ direction. Let
$H^2(X, \mathcal {O}_X)\cong H^0(X, \mathcal {O}_X(K_X))=0$
, the ‘if’ direction is [Reference KawakamiKaw22c, Theorem 2.8]. We prove the ‘only if’ direction. Let
![]() $f\colon Y\to X$
be a log resolution such that
$f\colon Y\to X$
be a log resolution such that ![]() lifts to
lifts to
![]() $W(k)$
. Since
$W(k)$
. Since
![]() $f_{*}(\Omega ^1_Y(\log \,E)\otimes \mathcal {O}_Y(f^{*}K_X))=\Omega _X^{[1]}(K_X)$
by [Reference Kawakami and TakamatsuKT24a, Theorem B], we have
$f_{*}(\Omega ^1_Y(\log \,E)\otimes \mathcal {O}_Y(f^{*}K_X))=\Omega _X^{[1]}(K_X)$
by [Reference Kawakami and TakamatsuKT24a, Theorem B], we have
![]() $H^0(X, \Omega _X^{[1]}(K_X))=H^0(Y,\Omega _Y^{1}(\log \,E)\otimes \mathcal {O}_Y(f^{*}K_X))$
. Then the vanishing follows from [Reference KawakamiKaw22a, Theorem 2.11].
$H^0(X, \Omega _X^{[1]}(K_X))=H^0(Y,\Omega _Y^{1}(\log \,E)\otimes \mathcal {O}_Y(f^{*}K_X))$
. Then the vanishing follows from [Reference KawakamiKaw22a, Theorem 2.11].
3.2 Global F-splitting: Proof of Theorem B
In the following proposition, we investigate F-splitting of F-pure canonical del Pezzo surfaces. For the proof, we confirm when the condition (2) of Proposition 3.2 is satisfied.
Proposition 3.5. Let X be an F-pure canonical del Pezzo surface. Suppose that one of the following holds.
-
(1)
 $K_X^2=1$
and
$K_X^2=1$
and
 $p>5$
.
$p>5$
. -
(2)
 $K_X^2=2$
and
$K_X^2=2$
and
 $p>3$
.
$p>3$
. -
(3)
 $K_X^2=3$
and
$K_X^2=3$
and
 $p>2$
.
$p>2$
. -
(4)
 $K_X^2=4$
.
$K_X^2=4$
.
Then X is F-split.
Proof. In each case, X is log liftable by [Reference Kawakami and NagaokaKN22, Theorem 1.7 (1)], and thus the condition (1) of Proposition 3.2 is satisfied. Thus, it suffices to confirm the condition (2) of Proposition 3.2, that is,
![]() $H^1(X, \Omega _X^{[1]}(pK_X))=0$
. By Serre duality of Cohen–Macaulay sheaves [Reference Kollár and MoriKM98, Theorem 5.71], we have
$H^1(X, \Omega _X^{[1]}(pK_X))=0$
. By Serre duality of Cohen–Macaulay sheaves [Reference Kollár and MoriKM98, Theorem 5.71], we have
![]() $H^1(X, \Omega _X^{[1]}(-pK_X))\cong H^1(X, \Omega _X^{[1]}(pK_X))$
. Since X has only hypersurface singularities,
$H^1(X, \Omega _X^{[1]}(-pK_X))\cong H^1(X, \Omega _X^{[1]}(pK_X))$
. Since X has only hypersurface singularities,
![]() $\Omega ^1_X$
is torsion-free by [Reference LipmanLip65, Section 8 (1)], and the natural map
$\Omega ^1_X$
is torsion-free by [Reference LipmanLip65, Section 8 (1)], and the natural map
![]() $\Omega _X^1\to \Omega _X^{[1]}$
is injective. Since
$\Omega _X^1\to \Omega _X^{[1]}$
is injective. Since
![]() $\mathcal {O}_X(-pK_X)$
is Cartier, we have an exact sequence
$\mathcal {O}_X(-pK_X)$
is Cartier, we have an exact sequence
for some coherent sheaf
![]() $\mathcal {C}$
satisfying
$\mathcal {C}$
satisfying
![]() $\dim \operatorname {\mathrm {Supp}}(\mathcal {C})=0$
. Since
$\dim \operatorname {\mathrm {Supp}}(\mathcal {C})=0$
. Since
![]() $H^1(X,\mathcal {C})=0$
, it suffices to show that
$H^1(X,\mathcal {C})=0$
, it suffices to show that
In what follows, we divide the proof into the cases according to (1)–(4) in the proposition.
The case (1): In this case, X is a hypersurface of ![]() of degree
of degree
![]() $6$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By [Reference MoriMor75, Theorem 1.7], the non-Gorenstein locus of P is
$6$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By [Reference MoriMor75, Theorem 1.7], the non-Gorenstein locus of P is
![]() $\{[0:0:0:1], [0:0:1:0]\}$
, and this locus coincides with the singular locus of P (Remark 3.6). Thus, X is contained in the smooth locus of P since it is Gorenstein. We define invertible sheaves
$\{[0:0:0:1], [0:0:1:0]\}$
, and this locus coincides with the singular locus of P (Remark 3.6). Thus, X is contained in the smooth locus of P since it is Gorenstein. We define invertible sheaves
![]() $\mathcal {O}_X(n)$
by
$\mathcal {O}_X(n)$
by
![]() $\mathcal {O}_P(n)|_X$
for all
$\mathcal {O}_P(n)|_X$
for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
By adjunction, we have
![]() $\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
$\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
By the conormal exact sequence, we have an exact sequence
Since
![]() $\mathcal {O}_X(p-6)$
is torsion-free and the first map is injective outside the singular points of X, we obtain an exact sequence
$\mathcal {O}_X(p-6)$
is torsion-free and the first map is injective outside the singular points of X, we obtain an exact sequence
Since
![]() $p\geq 7$
, we have
$p\geq 7$
, we have
![]() $H^2(X, \mathcal {O}_X(p-6))=0$
by Serre duality, and hence it suffices to show that
$H^2(X, \mathcal {O}_X(p-6))=0$
by Serre duality, and hence it suffices to show that
![]() $H^1(X, (\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X)=0$
. We have an exact sequence
$H^1(X, (\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X)=0$
. We have an exact sequence
Here, we obtain the first equality as follows:
since
![]() $\mathcal {O}_P(-6)$
is Cartier. In particular, the first term of the above exact sequence is torsion-free, and thus the first map is injective since it is injective outside the singular points of P.
$\mathcal {O}_P(-6)$
is Cartier. In particular, the first term of the above exact sequence is torsion-free, and thus the first map is injective since it is injective outside the singular points of P.
Moreover, since X is contained in the smooth locus of P, it follows that
![]() $\Omega ^{[1]}_P(p)|_X=(\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X$
. Thus, we obtain an exact sequence
$\Omega ^{[1]}_P(p)|_X=(\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X$
. Thus, we obtain an exact sequence
By Bott vanishing on P [Reference FujinoFuj07, Corollary 1.3], we have
since
![]() $p\geq 7$
. Therefore, we obtain
$p\geq 7$
. Therefore, we obtain
![]() $H^1(X, (\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X)=0$
.
$H^1(X, (\Omega ^1_{P}\otimes \mathcal {O}_P(p))|_X)=0$
.
The case (2): In this case, X is a hypersurface of ![]() of degree
of degree
![]() $4$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By [Reference MoriMor75, Theorem 1.7], the non-Gorenstein locus of P is
$4$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By [Reference MoriMor75, Theorem 1.7], the non-Gorenstein locus of P is
![]() $\{[0:0:0:1]\}$
, and this locus coincides with the singular locus of P (Remark 3.6). Thus, X is contained in the smooth locus of P since it is Gorenstein.
$\{[0:0:0:1]\}$
, and this locus coincides with the singular locus of P (Remark 3.6). Thus, X is contained in the smooth locus of P since it is Gorenstein.
By adjunction, we have
![]() $\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
$\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
As in the case (1), by the conormal exact sequence and the torsion-freeness of
![]() $\mathcal {O}_X(p-4)$
, we have an exact sequence
$\mathcal {O}_X(p-4)$
, we have an exact sequence
Since
![]() $p\geq 5$
, we have
$p\geq 5$
, we have
![]() $H^2(X, \mathcal {O}_X(p-4))=0$
, and it suffices to show that
$H^2(X, \mathcal {O}_X(p-4))=0$
, and it suffices to show that
As in the case (1), we have an exact sequence
By Bott vanishing [Reference FujinoFuj07, Corollary 1.3], we have
since
![]() $p\geq 5$
. Therefore, we obtain
$p\geq 5$
. Therefore, we obtain
![]() $H^1(X, \Omega ^1_{P}(p)|_X)=0$
.
$H^1(X, \Omega ^1_{P}(p)|_X)=0$
.
The case (3): In this case, X is a hypersurface of ![]() of degree
of degree
![]() $3$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By adjunction, we have
$3$
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By adjunction, we have
![]() $\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
$\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
![]() $H^{1}(X, \Omega ^1_X(p))=0$
. By the conormal exact sequence and the torsion-freeness of
$H^{1}(X, \Omega ^1_X(p))=0$
. By the conormal exact sequence and the torsion-freeness of
![]() $\mathcal {O}_X(p-3)$
, we have an exact sequence
$\mathcal {O}_X(p-3)$
, we have an exact sequence
Since
![]() $p\geq 3$
, we have
$p\geq 3$
, we have
![]() $H^2(X, \mathcal {O}_X(p-3))=0$
, and it suffices to show that
$H^2(X, \mathcal {O}_X(p-3))=0$
, and it suffices to show that
![]() $H^1(X, \Omega ^1_{P}(p)|_X)=0$
. We have an exact sequence
$H^1(X, \Omega ^1_{P}(p)|_X)=0$
. We have an exact sequence
By Bott vanishing [Reference FujinoFuj07, Corollary 1.3], we have
![]() $H^1(P, \Omega ^{1}_P(p))=0$
. By [Reference TotaroTot24, Proposition 1.3], we also have
$H^1(P, \Omega ^{1}_P(p))=0$
. By [Reference TotaroTot24, Proposition 1.3], we also have
![]() $H^2(P, \Omega ^{1}_P(p-3))=0$
since
$H^2(P, \Omega ^{1}_P(p-3))=0$
since
![]() $p\geq 3$
. Therefore, we obtain
$p\geq 3$
. Therefore, we obtain
![]() $H^1(X, \Omega ^1_{P}(p)|_X)=0$
.
$H^1(X, \Omega ^1_{P}(p)|_X)=0$
.
The case (4): In this case, X is a complete intersection of two quadric hypersurfaces Q and
![]() $Q'$
of
$Q'$
of ![]() [Reference Bernasconi and TanakaBT22, Theorem 2.15]. By adjunction, we have
[Reference Bernasconi and TanakaBT22, Theorem 2.15]. By adjunction, we have
![]() $\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
$\omega _X=\mathcal {O}_X(-1)$
, and thus we aim to show that
![]() $H^{1}(X, \Omega ^1_X(p))=0$
. By the conormal exact sequence and the torsion-freeness of
$H^{1}(X, \Omega ^1_X(p))=0$
. By the conormal exact sequence and the torsion-freeness of
![]() $\mathcal {O}_X(p-2)$
, we have an exact sequence
$\mathcal {O}_X(p-2)$
, we have an exact sequence
Since
![]() $p\geq 2$
, we have
$p\geq 2$
, we have
![]() $H^2(X, \mathcal {O}_X(p-2))=0$
, and hence it suffices to show that
$H^2(X, \mathcal {O}_X(p-2))=0$
, and hence it suffices to show that
![]() $H^1(X, (\Omega ^1_{Q}\otimes \mathcal {O}_{Q}(p))|_X)=0$
.
$H^1(X, (\Omega ^1_{Q}\otimes \mathcal {O}_{Q}(p))|_X)=0$
.
We define invertible sheaves
![]() $\mathcal {O}_Q(n)$
as
$\mathcal {O}_Q(n)$
as
![]() $\mathcal {O}_{P}(n)\otimes \mathcal {O}_{Q}$
for all
$\mathcal {O}_{P}(n)\otimes \mathcal {O}_{Q}$
for all
![]() $n\in \mathbb {Z}$
. We have an exact sequence
$n\in \mathbb {Z}$
. We have an exact sequence
Since X is regular in codimension one,
![]() $\Omega ^1_Q$
is torsion-free by [Reference LipmanLip65, Section 8 (1)]. Thus, we have an exact sequence
$\Omega ^1_Q$
is torsion-free by [Reference LipmanLip65, Section 8 (1)]. Thus, we have an exact sequence
Therefore, it suffices to show that
and in particular, the following claim finishes the proof of the case (4):
Claim. We have
-
(i)
 $H^1(Q, \Omega ^1_{Q}\otimes \mathcal {O}_Q(n))=0$
for every
$H^1(Q, \Omega ^1_{Q}\otimes \mathcal {O}_Q(n))=0$
for every
 $n\in \mathbb {Z} \setminus \{0\}$
and
$n\in \mathbb {Z} \setminus \{0\}$
and -
(ii)
 $H^2(Q, \Omega ^1_{Q}\otimes \mathcal {O}_Q(n))=0$
for every
$H^2(Q, \Omega ^1_{Q}\otimes \mathcal {O}_Q(n))=0$
for every
 $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
We have
-
(a)
 $H^i(P, \Omega ^1_{P}(n))=0$
for every
$H^i(P, \Omega ^1_{P}(n))=0$
for every
 $n \in \mathbb {Z} \setminus \{0\}$
and
$n \in \mathbb {Z} \setminus \{0\}$
and
 $i \in \{1, 2, 3\}$
, and
$i \in \{1, 2, 3\}$
, and -
(b)
 $H^j(P, \Omega ^1_P(n))=0$
for every
$H^j(P, \Omega ^1_P(n))=0$
for every
 $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
 $j \in \{2, 3\}$
.
$j \in \{2, 3\}$
.
Indeed, (a) follows from Bott vanishing and Serre duality. Then (a), together with [Reference TotaroTot24, Proposition 1.3], implies (b). By the following exact sequence
we get
-
(i)’
 $H^1(Q, \Omega ^1_{P}(n)|_{Q})=0$
for every
$H^1(Q, \Omega ^1_{P}(n)|_{Q})=0$
for every
 $n\in \mathbb {Z}\setminus \{0\}$
, and
$n\in \mathbb {Z}\setminus \{0\}$
, and -
(ii)’
 $H^2(Q, \Omega ^1_{P}(n)|_{Q})=0$
for every
$H^2(Q, \Omega ^1_{P}(n)|_{Q})=0$
for every
 $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
By the conormal exact sequence and the torsion-freeness of
![]() $\mathcal {O}_{P}(n-2)$
, we have an exact sequence
$\mathcal {O}_{P}(n-2)$
, we have an exact sequence
for every
![]() $n\in \mathbb {Z}$
. Since
$n\in \mathbb {Z}$
. Since
![]() $H^2(P, \mathcal {O}_P(n))=H^3(P, \mathcal {O}_P(n))=0$
for every
$H^2(P, \mathcal {O}_P(n))=H^3(P, \mathcal {O}_P(n))=0$
for every
![]() $n\in \mathbb {Z}$
, we have the claim.
$n\in \mathbb {Z}$
, we have the claim.
Remark 3.6. Take positive integers
![]() $q_1, q_2, q_3$
such that
$q_1, q_2, q_3$
such that
![]() $\mathrm {gcd}(q_1, q_2, q_3)=1$
. Set
$\mathrm {gcd}(q_1, q_2, q_3)=1$
. Set ![]() . Then it is well known (cf. [Reference FultonFul93, Section 2.2]) that P coincides with the projective
. Then it is well known (cf. [Reference FultonFul93, Section 2.2]) that P coincides with the projective
![]() $\mathbb {Q}$
-factorial toric threefold associated to the fan in
$\mathbb {Q}$
-factorial toric threefold associated to the fan in
![]() $\mathbb {R}^3$
that is generated by four rays
$\mathbb {R}^3$
that is generated by four rays
![]() $\mathbb {R} u, \mathbb {R} e_1, \mathbb {R} e_2, \mathbb {R} e_3$
, where
$\mathbb {R} u, \mathbb {R} e_1, \mathbb {R} e_2, \mathbb {R} e_3$
, where
![]() $e_1, e_2, e_3$
is the standard basis of
$e_1, e_2, e_3$
is the standard basis of
![]() $\mathbb {Z}^3$
and
$\mathbb {Z}^3$
and
In the above proof, we have used the results (1) and (2).
-
(1)
 ${\mathbb {P}}(1, 1, 2, 3)$
has exactly two singular points, which corresponds to the cones
${\mathbb {P}}(1, 1, 2, 3)$
has exactly two singular points, which corresponds to the cones
 $\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_2$
and
$\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_2$
and
 $\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_3$
[Reference Cox, Little and SchenckCLS11, Theorem 1.3.12].
$\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_3$
[Reference Cox, Little and SchenckCLS11, Theorem 1.3.12]. -
(2)
 ${\mathbb {P}}(1, 1, 1, 2)$
has a unique singular point, which corresponds to the cone
${\mathbb {P}}(1, 1, 1, 2)$
has a unique singular point, which corresponds to the cone
 $\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_2$
[Reference Cox, Little and SchenckCLS11, Theorem 1.3.12].
$\mathbb {R} u + \mathbb {R} e_1 + \mathbb {R} e_2$
[Reference Cox, Little and SchenckCLS11, Theorem 1.3.12].
From now on, we focus on the case where
![]() $K_X^2 \geq 5$
.
$K_X^2 \geq 5$
.
Proposition 3.7. The following assertions hold.
-
(1) Fix an integer m satisfying
 $1 \leq m \leq 5$
. Let
$1 \leq m \leq 5$
. Let
 $P_1,\ldots , P_m$
be distinct points on
$P_1,\ldots , P_m$
be distinct points on
 ${\mathbb {P}}^2$
such that the blowup X of
${\mathbb {P}}^2$
such that the blowup X of
 ${\mathbb {P}}^2$
along
${\mathbb {P}}^2$
along
 $\{P_1, \ldots , P_m\}$
is a weak del Pezzo surface. Then X is F-split.
$\{P_1, \ldots , P_m\}$
is a weak del Pezzo surface. Then X is F-split. -
(2) Fix an integer n satisfying
 $1 \leq n \leq 4$
. Let
$1 \leq n \leq 4$
. Let
 $Q_1,\ldots , Q_n$
be distinct points on
$Q_1,\ldots , Q_n$
be distinct points on
 ${\mathbb {P}}^1 \times {\mathbb {P}}^1$
such that the blowup X of
${\mathbb {P}}^1 \times {\mathbb {P}}^1$
such that the blowup X of
 ${\mathbb {P}}^1 \times {\mathbb {P}}^1$
along
${\mathbb {P}}^1 \times {\mathbb {P}}^1$
along
 $\{Q_1,\ldots , Q_n\}$
is a weak del Pezzo surface. Then X is F-split.
$\{Q_1,\ldots , Q_n\}$
is a weak del Pezzo surface. Then X is F-split.
Proof. Let us show (1). In what follows, we only treat the case when
![]() $m=5$
, as otherwise the problem is easier. Let L (resp.
$m=5$
, as otherwise the problem is easier. Let L (resp.
![]() $L'$
) be the line on
$L'$
) be the line on
![]() ${\mathbb {P}}^2$
passing through
${\mathbb {P}}^2$
passing through
![]() $P_1$
and
$P_1$
and
![]() $P_2$
(resp.
$P_2$
(resp.
![]() $P_3$
and
$P_3$
and
![]() $P_4$
). Since X is weak del Pezzo, we obtain
$P_4$
). Since X is weak del Pezzo, we obtain
![]() $L \neq L'$
. Pick a general line
$L \neq L'$
. Pick a general line
![]() $L"$
on
$L"$
on
![]() ${\mathbb {P}}^2$
passing through
${\mathbb {P}}^2$
passing through
![]() $P_5$
. Then
$P_5$
. Then
![]() $L+L'+L"$
is simple normal crossing. Therefore,
$L+L'+L"$
is simple normal crossing. Therefore,
![]() $({\mathbb {P}}^2, L+L'+L")$
is F-split (Example 2.7(2)), which implies that so is X (Proposition 2.4). Thus, (1) holds. The proof of (2) is similar to that of (1). Indeed, for each projection
$({\mathbb {P}}^2, L+L'+L")$
is F-split (Example 2.7(2)), which implies that so is X (Proposition 2.4). Thus, (1) holds. The proof of (2) is similar to that of (1). Indeed, for each projection
![]() $\mathrm {pr}_i \colon {\mathbb {P}}^1 \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$
, it is enough to take two fibers
$\mathrm {pr}_i \colon {\mathbb {P}}^1 \times {\mathbb {P}}^1 \to {\mathbb {P}}^1$
, it is enough to take two fibers
![]() $F_i$
and
$F_i$
and
![]() $F^{\prime }_i$
such that
$F^{\prime }_i$
such that
![]() $F_1 \cup F^{\prime }_1 \cup F_2 \cup F^{\prime }_2$
contains
$F_1 \cup F^{\prime }_1 \cup F_2 \cup F^{\prime }_2$
contains
![]() $\{Q_1,\ldots , Q_n\}$
(Example 2.7(3)).
$\{Q_1,\ldots , Q_n\}$
(Example 2.7(3)).
Proposition 3.8. Let X be a smooth weak del Pezzo surface satisfying
![]() $K_X^2 \geq 5$
. Then X is F-split.
$K_X^2 \geq 5$
. Then X is F-split.
Proof. By [Reference DolgachevDol12, Theorem 8.1.15], we may assume that there is a birational morphism
![]() $f\colon X \to {\mathbb {P}}^2$
. In what follows, we only treat the case when
$f\colon X \to {\mathbb {P}}^2$
. In what follows, we only treat the case when
![]() $K_X^2 = 5$
, as the other cases are simpler. There are the following five cases [Reference DolgachevDol12, Section 8.5].
$K_X^2 = 5$
, as the other cases are simpler. There are the following five cases [Reference DolgachevDol12, Section 8.5].
-
(i)
 $P, Q, R, S$
.
$P, Q, R, S$
. -
(ii)
 $P' \succ P, Q, R$
.
$P' \succ P, Q, R$
. -
(iii)
 $P' \succ P, Q' \succ Q$
.
$P' \succ P, Q' \succ Q$
. -
(iv)
 $P" \succ P' \succ P, Q$
.
$P" \succ P' \succ P, Q$
. -
(v)
 $P" \succ P' \succ P \succ Q$
.
$P" \succ P' \succ P \succ Q$
.
For the definition of
![]() $P' \succ P$
, we refer to [Reference DolgachevDol12, Section 7.3.2]. For example, in the case (iii), we have
$P' \succ P$
, we refer to [Reference DolgachevDol12, Section 7.3.2]. For example, in the case (iii), we have
![]() $X =Y" \to Y' \to Y = {\mathbb {P}}^2$
, where
$X =Y" \to Y' \to Y = {\mathbb {P}}^2$
, where
![]() $Y' = \operatorname {\mathrm {Bl}}_{P \amalg Q} Y$
,
$Y' = \operatorname {\mathrm {Bl}}_{P \amalg Q} Y$
,
![]() $Y" = \operatorname {\mathrm {Bl}}_{P' \amalg Q'}$
, and
$Y" = \operatorname {\mathrm {Bl}}_{P' \amalg Q'}$
, and
![]() $P'$
and
$P'$
and
![]() $Q'$
are points on
$Q'$
are points on
![]() $Y'$
lying over P and Q, respectively.
$Y'$
lying over P and Q, respectively.
The case (i) has been settled in Proposition 3.7, because we have
![]() $X = \operatorname {\mathrm {Bl}}_{P \amalg Q \amalg R \amalg S} {\mathbb {P}}^2$
for distinct points
$X = \operatorname {\mathrm {Bl}}_{P \amalg Q \amalg R \amalg S} {\mathbb {P}}^2$
for distinct points
![]() $P, Q, R, S \in {\mathbb {P}}^2$
in this case. In the case (ii),
$P, Q, R, S \in {\mathbb {P}}^2$
in this case. In the case (ii),
![]() $P, Q, R$
are distinct points on
$P, Q, R$
are distinct points on
![]() ${\mathbb {P}}^2$
, and we have
${\mathbb {P}}^2$
, and we have
![]() $X = \operatorname {\mathrm {Bl}}_{P'} Y'$
for
$X = \operatorname {\mathrm {Bl}}_{P'} Y'$
for
![]() $Y' := \operatorname {\mathrm {Bl}}_{P \amalg Q \amalg R} {\mathbb {P}}^2$
and a closed point
$Y' := \operatorname {\mathrm {Bl}}_{P \amalg Q \amalg R} {\mathbb {P}}^2$
and a closed point
![]() $P'$
lying over P. Take the line
$P'$
lying over P. Take the line ![]() passing through P and Q. Let
passing through P and Q. Let
![]() $L_2$
and
$L_2$
and
![]() $L_3$
be general lines passing through P and R, respectively. Then
$L_3$
be general lines passing through P and R, respectively. Then
![]() $({\mathbb {P}}^2, L_1+L_2+L_3)$
is F-split (Example 2.7(2)). Since
$({\mathbb {P}}^2, L_1+L_2+L_3)$
is F-split (Example 2.7(2)). Since
![]() $\Delta $
is effective for the divisor
$\Delta $
is effective for the divisor
![]() $\Delta $
defined by
$\Delta $
defined by
![]() $K_X +\Delta =f^*(K_{{\mathbb {P}}^2}+L_1+L_2+L_3)$
, it follows that X is F-split (Proposition 2.4). Similarly, (iii) is settled by taking the line
$K_X +\Delta =f^*(K_{{\mathbb {P}}^2}+L_1+L_2+L_3)$
, it follows that X is F-split (Proposition 2.4). Similarly, (iii) is settled by taking the line ![]() and general lines
and general lines
![]() $L_2$
and
$L_2$
and
![]() $L_3$
passing through P and Q, respectively.
$L_3$
passing through P and Q, respectively.
Let us treat the case (iv). In this case, we have
![]() $X = Y"' \to Y" \to Y' \to Y={\mathbb {P}}^2$
, where
$X = Y"' \to Y" \to Y' \to Y={\mathbb {P}}^2$
, where ![]() ,
, ![]() , and
, and
![]() $P'$
(resp.
$P'$
(resp.
![]() $P"$
) is lying over P (resp.
$P"$
) is lying over P (resp.
![]() $P'$
). Let
$P'$
). Let
![]() $L_1$
be the line on
$L_1$
be the line on
![]() $Y={\mathbb {P}}^2$
such that
$Y={\mathbb {P}}^2$
such that
![]() $P \in L_1$
and
$P \in L_1$
and
![]() $P' \in L^{\prime }_1$
for the proper transform
$P' \in L^{\prime }_1$
for the proper transform
![]() $L^{\prime }_1$
of
$L^{\prime }_1$
of
![]() $L_1$
on
$L_1$
on
![]() $Y'$
. Let
$Y'$
. Let
![]() $L_2$
and
$L_2$
and
![]() $L_3$
be general lines passing through P and Q, respectively. Then we can check that the divisor
$L_3$
be general lines passing through P and Q, respectively. Then we can check that the divisor
![]() $\Delta $
defined by
$\Delta $
defined by
![]() $K_X +\Delta =f^*(K_{{\mathbb {P}}^2}+L_1 +L_2 +L_3)$
is effective. Since
$K_X +\Delta =f^*(K_{{\mathbb {P}}^2}+L_1 +L_2 +L_3)$
is effective. Since
![]() $({\mathbb {P}}^2, L_1 +L_2 +L_3)$
is F-split (Example 2.7(2)), so is X. This completes the proof for the case (iv).
$({\mathbb {P}}^2, L_1 +L_2 +L_3)$
is F-split (Example 2.7(2)), so is X. This completes the proof for the case (iv).
Let us consider the case (v). In this case, we apply a similar method to that of (iv) after replacing
![]() ${\mathbb {P}}^2$
by
${\mathbb {P}}^2$
by
![]() $\mathbb {F}_1$
. We have a sequence of one-point blowups:
$\mathbb {F}_1$
. We have a sequence of one-point blowups:
where ![]() ,
, ![]() ,
, ![]() , and
, and
![]() $P, P', P"$
are lying over
$P, P', P"$
are lying over
![]() $Q, P, P'$
, respectively. For the
$Q, P, P'$
, respectively. For the
![]() $(-1)$
-curve C on Y, we have
$(-1)$
-curve C on Y, we have
![]() $P\in C$
. It is well known that there is another section
$P\in C$
. It is well known that there is another section
![]() $\widetilde C$
of the
$\widetilde C$
of the
![]() ${\mathbb {P}}^1$
-bundle
${\mathbb {P}}^1$
-bundle
![]() $\pi \colon Y=\mathbb {F}_1 \to B={\mathbb {P}}^1$
such that
$\pi \colon Y=\mathbb {F}_1 \to B={\mathbb {P}}^1$
such that
![]() $C \cap \widetilde {C} = \emptyset $
and
$C \cap \widetilde {C} = \emptyset $
and
![]() $\widetilde {C}^2 =1$
. Let F is a fiber of
$\widetilde {C}^2 =1$
. Let F is a fiber of
![]() $\pi $
. Since
$\pi $
. Since
![]() $(K_Y+C+\widetilde {C})\cdot F=0$
, there exists
$(K_Y+C+\widetilde {C})\cdot F=0$
, there exists
![]() $n\in \mathbb {Z}$
such that
$n\in \mathbb {Z}$
such that
![]() $K_Y+C+\widetilde {C}\sim nF$
. Then
$K_Y+C+\widetilde {C}\sim nF$
. Then
![]() $n=C\cdot nF =C\cdot (K_Y+C+\widetilde {C})=-2$
. Since the proper transform
$n=C\cdot nF =C\cdot (K_Y+C+\widetilde {C})=-2$
. Since the proper transform
![]() $C'$
of C on
$C'$
of C on
![]() $Y'$
satisfies
$Y'$
satisfies
![]() $C^\prime 2=-2$
, we obtain
$C^\prime 2=-2$
, we obtain
-
(1)
 $P' \not \in C'$
,
$P' \not \in C'$
,
as otherwise, the proper transform
![]() $C"$
of
$C"$
of
![]() $C'$
on
$C'$
on
![]() $Y"$
would satisfy
$Y"$
would satisfy
![]() $C^\prime \prime 2 =-3$
, which contradicts the fact that
$C^\prime \prime 2 =-3$
, which contradicts the fact that
![]() $Y"$
is weak del Pezzo.
$Y"$
is weak del Pezzo.
We now treat the case when
![]() $P' \in F^{\prime }_P$
, where
$P' \in F^{\prime }_P$
, where
![]() $F^{\prime }_P$
denotes the proper transform of the fiber
$F^{\prime }_P$
denotes the proper transform of the fiber
![]() $F_P$
of
$F_P$
of
![]() $\pi \colon Y =\mathbb {F}_1 \to {\mathbb {P}}^1$
passing through P. Let
$\pi \colon Y =\mathbb {F}_1 \to {\mathbb {P}}^1$
passing through P. Let
![]() $\widetilde F$
be a general fiber of
$\widetilde F$
be a general fiber of
![]() $\pi $
. As we have seen above,
$\pi $
. As we have seen above,
![]() $K_Y+{\widetilde F}+ C+F_P +\widetilde C \sim 0$
. Since
$K_Y+{\widetilde F}+ C+F_P +\widetilde C \sim 0$
. Since
![]() $\widetilde F$
is nef and
$\widetilde F$
is nef and
![]() $\mathbb {F}_1$
is toric, we obtain
$\mathbb {F}_1$
is toric, we obtain
![]() $H^1(\mathbb {F}_1, \mathcal {O}_{F_1}(\widetilde F))=0$
by [Reference TotaroTot24, Proposition 1.3]. Moreover,
$H^1(\mathbb {F}_1, \mathcal {O}_{F_1}(\widetilde F))=0$
by [Reference TotaroTot24, Proposition 1.3]. Moreover,
![]() $(\widetilde F, (C+F_P +\widetilde C)|_{\widetilde F})=( \widetilde {F}, C|_{\widetilde F}+\widetilde C|_{\widetilde F})$
is F-split (Example 2.7 (1)). Thus,
$(\widetilde F, (C+F_P +\widetilde C)|_{\widetilde F})=( \widetilde {F}, C|_{\widetilde F}+\widetilde C|_{\widetilde F})$
is F-split (Example 2.7 (1)). Thus,
![]() $(Y, C+F_P +\widetilde C + \widetilde F)$
is F-split (Proposition 2.6), which implies that X is F-split (Proposition 2.4). In what follows, we assume that
$(Y, C+F_P +\widetilde C + \widetilde F)$
is F-split (Proposition 2.6), which implies that X is F-split (Proposition 2.4). In what follows, we assume that
-
(2)
 $P' \not \in F^{\prime }_P$
for the proper transform
$P' \not \in F^{\prime }_P$
for the proper transform
 $F^{\prime }_P$
of the fiber
$F^{\prime }_P$
of the fiber
 $F_P$
of
$F_P$
of
 $\pi : Y =\mathbb {F}_1 \to {\mathbb {P}}^1$
passing through P.
$\pi : Y =\mathbb {F}_1 \to {\mathbb {P}}^1$
passing through P.
Claim. There is a section D of
![]() $\pi \colon Y=\mathbb {F}_1 \to {\mathbb {P}}^1$
such that
$\pi \colon Y=\mathbb {F}_1 \to {\mathbb {P}}^1$
such that
-
(a)
 $D \sim \widetilde C+F$
,
$D \sim \widetilde C+F$
, -
(b)
 $P \in D$
, and
$P \in D$
, and -
(c)
 $P' \in D'$
for the proper transform
$P' \in D'$
for the proper transform
 $D'$
of D on
$D'$
of D on
 $Y'$
.
$Y'$
.
Proof of Claim.
Since
![]() $\widetilde C+F$
is an ample Cartier divisor on
$\widetilde C+F$
is an ample Cartier divisor on
![]() $Y=\mathbb {F}_1$
, it follows that
$Y=\mathbb {F}_1$
, it follows that
![]() $|\widetilde C+F|$
is very ample [Reference HartshorneHar77, Ch. V, Corollary 2.18]. Then there is an effective Cartier divisor D on
$|\widetilde C+F|$
is very ample [Reference HartshorneHar77, Ch. V, Corollary 2.18]. Then there is an effective Cartier divisor D on
![]() $Y = \mathbb {F}_1$
satisfying (a)–(d).
$Y = \mathbb {F}_1$
satisfying (a)–(d).
-
(d) D is smooth at P.
In fact, since
![]() $|\widetilde C+F|$
is very ample, the elements of
$|\widetilde C+F|$
is very ample, the elements of
![]() $H^0(Y, \mathcal {O}_Y(\widetilde C+F))$
separate tangent vectors. Let
$H^0(Y, \mathcal {O}_Y(\widetilde C+F))$
separate tangent vectors. Let
![]() $s_{P'}\in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
is an element that corresponds to
$s_{P'}\in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
is an element that corresponds to
![]() $P'$
. We take D as a divisor of zeros of a global section
$P'$
. We take D as a divisor of zeros of a global section
![]() $s\in H^0(Y, \mathcal {O}_Y(\widetilde C+F))$
that maps to
$s\in H^0(Y, \mathcal {O}_Y(\widetilde C+F))$
that maps to
![]() $s_{P'}\in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
. Then (a)–(c) are satisfied. Since
$s_{P'}\in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
. Then (a)–(c) are satisfied. Since
![]() $s \in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
is non-zero, the divisor D is smooth at P, i.e., (d) is satisfied. Since
$s \in \mathfrak {m}_P/\mathfrak {m}^2_{P}$
is non-zero, the divisor D is smooth at P, i.e., (d) is satisfied. Since
![]() $D \cdot F = (\widetilde C + F) \cdot F =1$
, we can write
$D \cdot F = (\widetilde C + F) \cdot F =1$
, we can write
![]() $D= D_0 + F_1 + \cdots +F_r$
, where
$D= D_0 + F_1 + \cdots +F_r$
, where
![]() $r \geq 0$
,
$r \geq 0$
,
![]() $D_0$
is a section of
$D_0$
is a section of
![]() $\pi \colon Y = \mathbb {F}_1 \to {\mathbb {P}}^1$
, and each
$\pi \colon Y = \mathbb {F}_1 \to {\mathbb {P}}^1$
, and each
![]() $F_i$
is a fiber of
$F_i$
is a fiber of
![]() $\pi $
. It suffices to prove
$\pi $
. It suffices to prove
![]() $r=0$
. Suppose
$r=0$
. Suppose
![]() $r>0$
. The following holds:
$r>0$
. The following holds:
We now treat the case when
![]() $D_0 \neq C$
. In this case,
$D_0 \neq C$
. In this case,
![]() $D_0 \cdot C \geq 0$
and (3.8.1) imply
$D_0 \cdot C \geq 0$
and (3.8.1) imply
![]() $r=1$
and
$r=1$
and
![]() $D_0 \cdot C =0$
. Hence, we get
$D_0 \cdot C =0$
. Hence, we get
![]() $D_0 \cap C = \emptyset $
. Since
$D_0 \cap C = \emptyset $
. Since
![]() $P\in C$
, we have
$P\in C$
, we have
![]() $P\notin D_0$
. By (b), we obtain
$P\notin D_0$
. By (b), we obtain
![]() $P\in D=D_0+F_1$
, and thus
$P\in D=D_0+F_1$
, and thus
![]() $P\in F_1$
. Hence,
$P\in F_1$
. Hence,
![]() $D = D_0 +F_P$
, where
$D = D_0 +F_P$
, where
![]() $F_P$
denotes the fiber passing through P. Since
$F_P$
denotes the fiber passing through P. Since
![]() $P'\notin C'$
, we obtain
$P'\notin C'$
, we obtain
![]() $P'\in D'\setminus C'\subset F^{\prime }_P$
. This contradicts (2).
$P'\in D'\setminus C'\subset F^{\prime }_P$
. This contradicts (2).
Hence, we may assume that
![]() $D_0 =C$
. We then get
$D_0 =C$
. We then get
![]() $D = C +F_1 + \cdots +F_r$
. Since
$D = C +F_1 + \cdots +F_r$
. Since
![]() $P\in C$
, we obtain
$P\in C$
, we obtain
![]() $P \not \in F_1 \cup \cdots \cup F_r$
by (d). Then
$P \not \in F_1 \cup \cdots \cup F_r$
by (d). Then
![]() $P' \not \in F^{\prime }_1 \cup \cdots \cup F^{\prime }_r$
, where
$P' \not \in F^{\prime }_1 \cup \cdots \cup F^{\prime }_r$
, where
![]() $F^{\prime }_1, F^{\prime }_2,\ldots , F^{\prime }_r$
are proper transforms of
$F^{\prime }_1, F^{\prime }_2,\ldots , F^{\prime }_r$
are proper transforms of
![]() $F_1, F_2,\ldots , F_r$
on
$F_1, F_2,\ldots , F_r$
on
![]() $Y'$
, and thus we obtain
$Y'$
, and thus we obtain
![]() $P'\in D'\setminus \{F^{\prime }_1 \cup \cdots \cup F^{\prime }_r\}\subset C'$
by (c). This contradicts (1). This completes the proof of the claim.
$P'\in D'\setminus \{F^{\prime }_1 \cup \cdots \cup F^{\prime }_r\}\subset C'$
by (c). This contradicts (1). This completes the proof of the claim.
We have
![]() $C \cdot D = 1$
. Hence,
$C \cdot D = 1$
. Hence,
![]() $C \cap D = P$
and
$C \cap D = P$
and
![]() $C+ D$
is a simple normal crossing divisor. Since both C and D are sections of
$C+ D$
is a simple normal crossing divisor. Since both C and D are sections of
![]() $\pi \colon Y = \mathbb {F}_1 \to {\mathbb {P}}^1$
, it follows that
$\pi \colon Y = \mathbb {F}_1 \to {\mathbb {P}}^1$
, it follows that
![]() $C+D+\widetilde F$
is still simple normal crossing for a general fiber
$C+D+\widetilde F$
is still simple normal crossing for a general fiber
![]() $\widetilde F$
of
$\widetilde F$
of
![]() $\pi $
. Then we see that
$\pi $
. Then we see that
![]() $(Y, C+D+\widetilde F)$
is F-split (Proposition 2.6, Example 2.7(1)). Since the divisor
$(Y, C+D+\widetilde F)$
is F-split (Proposition 2.6, Example 2.7(1)). Since the divisor
![]() $\Delta $
defined by
$\Delta $
defined by
![]() $K_X +\Delta = f^*(K_Y+C+D+\widetilde F)$
is effective, X is F-split (Proposition 2.4). This completes the proof of Proposition 3.8.
$K_X +\Delta = f^*(K_Y+C+D+\widetilde F)$
is effective, X is F-split (Proposition 2.4). This completes the proof of Proposition 3.8.
3.3 Global F-regularity: Proof of Theorem A
In this subsection, we deduce Theorem A from Theorem B.
Lemma 3.9. Let X be a canonical del Pezzo surface. Suppose that one of the following holds.
-
(1)
 $p>5$
$p>5$
-
(2)
 $K_X^2\geq 2$
and
$K_X^2\geq 2$
and
 $p>3$
.
$p>3$
. -
(3)
 $K_X^2\geq 4$
and
$K_X^2\geq 4$
and
 $p>2$
.
$p>2$
. -
(4)
 $K_X^2\geq 5$
.
$K_X^2\geq 5$
.
Then X is strongly F-regular.
Remark 3.10. Combining [Reference Kawakami and NagaokaKN23, Table 1] and [Reference Kawakami and TakamatsuKT24a, Table 1], we can see that the assumption of p is optimal for each degree.
Proof. Strongly F-regular surface singularities are completely classified by Hara [Reference HaraHar98b, Theorem 1.1]. In what follows, we confirm the singularities on X satisfying one of (1)–(4) are all strongly F-regular.
(1) follows from [Reference HaraHar98b, Theorem 1.1]. In what follows, let
![]() $f\colon Y\to X$
be the minimal resolution. Then Y is a smooth weak del Pezzo surface (Subsection 2.1.2), and Y is obtained by a blowup of
$f\colon Y\to X$
be the minimal resolution. Then Y is a smooth weak del Pezzo surface (Subsection 2.1.2), and Y is obtained by a blowup of
![]() ${\mathbb {P}}^2$
at some points [Reference DolgachevDol12, Theorem 8.1.15]. We have holds.
${\mathbb {P}}^2$
at some points [Reference DolgachevDol12, Theorem 8.1.15]. We have holds.
We prove (2). Since
![]() $K_Y^2=K_X^2\geq 2$
, we have
$K_Y^2=K_X^2\geq 2$
, we have
![]() $\rho (Y) = 10 -K_Y^2 \leq 8$
. Thus, the number of the
$\rho (Y) = 10 -K_Y^2 \leq 8$
. Thus, the number of the
![]() $(-2)$
-curves contracted by f is at most
$(-2)$
-curves contracted by f is at most
![]() $8-\rho (X)\leq 7$
. Therefore, X does not have canonical singularities of
$8-\rho (X)\leq 7$
. Therefore, X does not have canonical singularities of
![]() $E_8$
-type. Then X is strongly F-regular by [Reference HaraHar98b, Theorem 1.1] since
$E_8$
-type. Then X is strongly F-regular by [Reference HaraHar98b, Theorem 1.1] since
![]() $p>3$
(see also [Reference Kawakami and TakamatsuKT24a, Table 1]).
$p>3$
(see also [Reference Kawakami and TakamatsuKT24a, Table 1]).
Next, we prove (3). Since
![]() $K_Y^2=K_X^2\geq 4$
, we have
$K_Y^2=K_X^2\geq 4$
, we have
![]() $\rho (Y) = 10 -K_Y^2\leq 6$
. Thus, the number of the
$\rho (Y) = 10 -K_Y^2\leq 6$
. Thus, the number of the
![]() $(-2)$
-curves contracted by f is at most
$(-2)$
-curves contracted by f is at most
![]() $6-\rho (X)\leq 5$
. Therefore, X does not have canonical singularities of E-type. Then X is strongly F-regular by [Reference HaraHar98b, Theorem 1.1] since
$6-\rho (X)\leq 5$
. Therefore, X does not have canonical singularities of E-type. Then X is strongly F-regular by [Reference HaraHar98b, Theorem 1.1] since
![]() $p>2$
(see also [Reference Kawakami and TakamatsuKT24a, Table 1]).
$p>2$
(see also [Reference Kawakami and TakamatsuKT24a, Table 1]).
Finally, we prove (4). Since
![]() $K_Y^2=K_X^2\geq 5$
, we have
$K_Y^2=K_X^2\geq 5$
, we have
![]() $\rho (Y) = 10 -K_Y^2\leq 5$
. Thus, the number of the
$\rho (Y) = 10 -K_Y^2\leq 5$
. Thus, the number of the
![]() $(-2)$
-curves contracted by f is at most
$(-2)$
-curves contracted by f is at most
![]() $5-\rho (X)\leq 4$
. If
$5-\rho (X)\leq 4$
. If
![]() $\rho (X)\geq 2$
, then X has only A-type singularities, which are strongly F-regular [Reference HaraHar98b, Theorem 1.1]. If
$\rho (X)\geq 2$
, then X has only A-type singularities, which are strongly F-regular [Reference HaraHar98b, Theorem 1.1]. If
![]() $\rho (X)=1$
, then X has only A-type singularities by [Reference Kawakami and NagaokaKN23, Theorem 1.1].
$\rho (X)=1$
, then X has only A-type singularities by [Reference Kawakami and NagaokaKN23, Theorem 1.1].
Acknowledgements
The authors express their gratitude to Burt Totaro and the anonymous referee for valuable comments.
Funding statement
Kawakami was supported by JSPS KAKENHI Grant number JP22KJ1771 and JP24K16897. Tanaka was supported by JSPS KAKENHI Grant number JP22H01112 and JP23K03028.
Competing interest
The authors have no competing interest to declare.