Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-30T09:30:05.573Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORIFYING RATIONALIZATION

Part of: Categories and geometry Higher algebraic $K$-theory

Published online by Cambridge University Press:  09 January 2020

CLARK BARWICK ,
SAUL GLASMAN ,
MARC HOYOIS ,
DENIS NARDIN  and
JAY SHAH
CLARK BARWICK
Affiliation:
School of Mathematics, University of Edinburgh, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK; [email protected]
MARC HOYOIS
Affiliation:
Department of Mathematics, University of Southern California, 3620 South Vermont Avenue, Los Angeles, CA 90089, USA; [email protected]
DENIS NARDIN
Affiliation:
Département de Mathématiques, Institut Galilée, Université Paris 13, 99 av. J.B. Clément, 93430 Villetaneuse, France; [email protected]
JAY SHAH
Affiliation:
Department of Mathematics, University of Notre Dame, 255 Hurley, Notre Dame, IN 46556, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct, for any set of primes 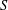$S$, a triangulated category (in fact a stable 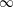$\infty$-category) whose Grothendieck group is 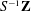$S^{-1}\mathbf{Z}$. More generally, for any exact 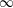$\infty$-category 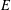$E$, we construct an exact 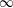$\infty$-category 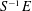$S^{-1}E$ of equivariant sheaves on the Cantor space with respect to an action of a dense subgroup of the circle. We show that this 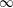$\infty$-category is precisely the result of categorifying division by the primes in 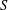$S$. In particular, 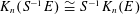$K_{n}(S^{-1}E)\cong S^{-1}K_{n}(E)$.

MSC classification

Primary: 19D99: None of the above, but in this section
Secondary: 18F25: Algebraic $K$-theory and $L$-theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e42
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Barwick, C., ‘Multiplicative structures on algebraic K-theory’, Doc. Math. 20 (2015), 859–878.Google Scholar
Barwick, C., ‘On exact ∞-categories and the theorem of the heart’, Compos. Math. 151(11) (2015), 2160–2186.Google Scholar
Barwick, C., ‘Spectral Mackey functors and equivariant algebraic K-theory (I)’, Adv. Math. 304(2) (2017), 646–727. Preprint, 2014, arXiv:1404.0108.Google Scholar
Berthelot, P., Grothendieck, A. and Illusie, L., Théorie des intersections et théorème de Riemann–Roch, Séminaire de Géométrie Algébrique du Bois Marie, 1966–67 (SGA 6). Avec la collaboration de D. Ferrand, J. P. Jouanolou, O. Jussila, S. Kleiman, M. Raynaud, J. P. Serre. Lecture Notes in Mathematics, Vol. 225. Springer-Verlag, Berlin, 1966–67.Google Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. Éc. Norm. Supér (4) 7 (1975), 235–272. 1974.Google Scholar
Gaitsgory, D., ‘Ind-coherent sheaves’, Mosc. Math. J. 13(3) (2013), 399–528.Google Scholar
Khovanov, M., ‘Linearization and categorification’, Preprint, 2016, arXiv:1603.08223.Google Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Thomason, R. W. and Trobaugh, T., ‘Higher algebraic K-theory of schemes and of derived categories’, inThe Grothendieck Festschrift, Vol. III, Progress in Mathematics, 88 (Birkhäuser Boston, Boston, MA, 1990), 247–435.Google Scholar