This article extends the validity of the conditional likelihood ratio (CLR) test developed by Moreira (2003, Econometrica 71(4), 1027-–1048) to instrumental variable regression models with unknown homoskedastic error variance and many weak instruments. We argue that the conventional CLR test with estimated error variance loses exact similarity and is asymptotically invalid in this setting. We propose a modified critical value function for the likelihood ratio (LR) statistic with estimated error variance, and prove that our modified test achieves asymptotic validity under many weak instruments asymptotics. Our critical value function is constructed by representing the LR using four statistics, instead of two as in Moreira (2003, Econometrica 71(4), 1027-–1048). A simulation study illustrates the desirable finite sample properties of our test.

In this paper, we consider estimating spot/instantaneous volatility matrices of high-frequency data collected for a large number of assets. We first combine classic nonparametric kernel-based smoothing with a generalized shrinkage technique in the matrix estimation for noise-free data under a uniform sparsity assumption, a natural extension of the approximate sparsity commonly used in the literature. The uniform consistency property is derived for the proposed spot volatility matrix estimator with convergence rates comparable to the optimal minimax one. For high-frequency data contaminated by microstructure noise, we introduce a localized pre-averaging estimation method that reduces the effective magnitude of the noise. We then use the estimation tool developed in the noise-free scenario and derive the uniform convergence rates for the developed spot volatility matrix estimator. We further combine kernel smoothing with the shrinkage technique to estimate the time-varying volatility matrix of the high-dimensional noise vector. In addition, we consider large spot volatility matrix estimation in time-varying factor models with observable risk factors and derive the uniform convergence property. We provide numerical studies including simulation and empirical application to examine the performance of the proposed estimation methods in finite samples.

This study proposes two novel time-varying model-averaging methods for time-varying parameter regression models. When the number of predictors is small, we propose a novel time-varying complete subset-averaging (TVCSA) procedure, where the optimal time-varying subset size is obtained by minimizing the local leave-h-out cross-validation criterion. The TVCSA method is asymptotically optimal for achieving the lowest possible local mean squared error. When the number of predictors is relatively large, we propose a factor TVCSA method to reduce the computational burden by first reducing the dimension of predictors by extracting a few factors using principal component analysis and then obtaining the TVCSA forecasts from time-varying models with the generated factors. We show that the TVCSA estimator remains asymptotically optimal in the presence of generated factors. Monte Carlo simulation studies have provided favorable evidence for the TVCSA methods relative to the popular model-averaging methods in the literature. Empirical applications to equity premiums and inflation forecasting highlight the practical merits of the proposed methods.

We propose a family of weighted statistics based on the CUSUM process of the WLS residuals for the online detection of changepoints in a Random Coefficient Autoregressive model, using both the standard CUSUM and the Page-CUSUM process. We derive the asymptotics under the null of no changepoint for all possible weighing schemes, including the case of the standardized CUSUM, for which we derive a Darling–Erdös-type limit theorem; our results guarantee the procedure-wise size control under both an open-ended and a closed-ended monitoring. In addition to considering the standard RCA model with no covariates, we also extend our results to the case of exogenous regressors. Our results can be applied irrespective of (and with no prior knowledge required as to) whether the observations are stationary or not, and irrespective of whether they change into a stationary or nonstationary regime. Hence, our methodology is particularly suited to detect the onset, or the collapse, of a bubble or an epidemic. Our simulations show that our procedures, especially when standardising the CUSUM process, can ensure very good size control and short detection delays. We complement our theory by studying the online detection of breaks in epidemiological and housing prices series.

Modern data analysis depends increasingly on estimating models via flexible high-dimensional or nonparametric machine learning methods, where the identification of structural parameters is often challenging and untestable. In linear settings, this identification hinges on the completeness condition, which requires the nonsingularity of a high-dimensional matrix or operator and may fail for finite samples or even at the population level. Regularized estimators provide a solution by enabling consistent estimation of structural or average structural functions, sometimes even under identification failure. We show that the asymptotic distribution in these cases can be nonstandard. We develop a comprehensive theory of regularized estimators, which include methods such as high-dimensional ridge regularization, gradient descent, and principal component analysis (PCA). The results are illustrated for high-dimensional and nonparametric instrumental variable regressions and are supported through simulation experiments.

We study minimax regret treatment rules under matched treatment assignment in a setup where a policymaker, informed by a sample of size N, needs to decide between T different treatments for a 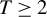$T\geq 2$. Randomized rules are allowed for. We show that the generalization of the minimax regret rule derived in Schlag (2006, ELEVEN—Tests needed for a recommendation, EUI working paper) and Stoye (2009, Journal of Econometrics 151, 70–81) for the case $T=2$ is minimax regret for general finite 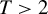$T>2$ and also that the proof structure via the Nash equilibrium and the “coarsening” approaches generalizes as well. We also show by example, that in the case of random assignment the generalization of the minimax rule in Stoye (2009, Journal of Econometrics 151, 70–81) to the case 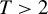$T>2$ is not necessarily minimax regret and derive minimax regret rules for a few small sample cases, e.g., for 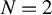$N=2$ when 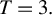$T=3.$

In the case where a covariate x is included, it is shown that a minimax regret rule is obtained by using minimax regret rules in the “conditional-on-x” problem if the latter are obtained as Nash equilibria.

A new explicit solution representation is provided for ARMA recursions with drift and either deterministically or stochastically varying coefficients. It is expressed in terms of the determinants of banded Hessenberg matrices and, as such, is an explicit function of the coefficients. In addition to computational efficiency, the proposed solution provides a more explicit analysis of the fundamental properties of such processes, including their Wold–Cramér decomposition, their covariance structure, and their asymptotic stability and efficiency. Explicit formulae for optimal linear forecasts based either on finite or infinite sequences of past observations are provided. The practical significance of the theoretical results in this work is illustrated with an application to U.S. inflation data. The main finding is that inflation persistence increased after 1976, whereas from 1986 onward, the persistence declines and stabilizes to even lower levels than the pre-1976 period.

This paper proposes a consistent nonparametric test with good sampling properties to detect instantaneous causality between vector autoregressive (VAR) variables with time-varying variances. The new test takes the form of the U-statistic, and has a limiting standard normal distribution under the null. We further show that the test is consistent against any fixed alternatives, and has nontrivial asymptotic power against a class of local alternatives with a rate slower than $T^{-1/2}$. We also propose a wild bootstrap procedure to better approximate the finite sample null distribution of the test statistic. Monte Carlo experiments are conducted to highlight the merits of the proposed test relative to other popular tests in finite samples. Finally, we apply the new test to investigate the instantaneous causality relationship between money supply and inflation rates in the USA.

We consider bootstrap inference in predictive (or Granger-causality) regressions when the parameter of interest may lie on the boundary of the parameter space, here defined by means of a smooth inequality constraint. For instance, this situation occurs when the definition of the parameter space allows for the cases of either no predictability or sign-restricted predictability. We show that in this context constrained estimation gives rise to bootstrap statistics whose limit distribution is, in general, random, and thus distinct from the limit null distribution of the original statistics of interest. This is due to both (i) the possible location of the true parameter vector on the boundary of the parameter space and (ii) the possible non-stationarity of the posited predicting (resp. Granger-causing) variable. We discuss a modification of the standard fixed-regressor wild bootstrap scheme where the bootstrap parameter space is shifted by a data-dependent function in order to eliminate the portion of limiting bootstrap randomness attributable to the boundary and prove validity of the associated bootstrap inference under non-stationarity of the predicting variable as the only remaining source of limiting bootstrap randomness. Our approach, which is initially presented in a simple location model, has bearing on inference in parameter-on-the-boundary situations beyond the predictive regression problem.

This study proposes a test for coefficient randomness in autoregressive models where the autoregressive coefficient is local to unity, which is empirically relevant given earlier work. Under this specification, we analyze the effect of the correlation between the random coefficient and disturbance on the properties of tests, a matter that remains largely unexplored in the literature. Our analysis reveals that tests proposed in earlier studies can have poor power when the correlation is moderate to large. The test proposed here is designed to have power functions robust to the correlation. A modified version of the test is suggested that can be applied when the disturbance is serially correlated and conditionally heteroskedastic. The test is shown to have better power properties than existing ones in large and finite samples.

The Least Trimmed Squares (LTS) regression estimator is known to be very robust to the presence of “outliers”. It is based on a clear and intuitive idea: in a sample of size n, it searches for the h-subsample of observations with the smallest sum of squared residuals. The remaining $n-h$ observations are declared “outliers”. Fast algorithms for its computation exist. Nevertheless, the existing asymptotic theory for LTS, based on the traditional $\epsilon $-contamination model, shows that the asymptotic behavior of both regression and scale estimators depend on nuisance parameters. Using a recently proposed new model, in which the LTS estimator is maximum likelihood, we show that the asymptotic behavior of both the LTS regression and scale estimators are free of nuisance parameters. Thus, with the new model as a benchmark, standard inference procedures apply while allowing a broad range of contamination.

This article examines high-dimensional covariates in regression discontinuity design (RDD) analysis. We introduce estimation and inference methods for the RDD models that incorporate covariate selection while maintaining stability across various numbers of covariates. The proposed methods combine a localization approach using kernel weights with $\ell _{1}$-penalization to handle high-dimensional covariates. We provide both theoretical and numerical evidence demonstrating the efficacy of our methods. Theoretically, we present risk and coverage properties for our point estimation and inference methods. Conditions are given under which the proposed estimator becomes more efficient than the conventional covariate adjusted estimator at the cost of an additional sparsity condition. Numerically, our simulation experiments and empirical examples show the robust behaviors of the proposed methods to the number of covariates in terms of bias and variance for point estimation and coverage probability and interval length for inference.

We consider the problem of identifying the parameters of a time-homogeneous bivariate Markov chain when only one of the two variables is observable. We show that, subject to conditions that we spell out, the transition kernel and the distribution of the initial condition are uniquely recoverable (up to an arbitrary relabelling of the state space of the latent variable) from the joint distribution of four (or more) consecutive time-series observations. The result is, therefore, applicable to (short) panel data as well as to (stationary) time series data.

Since the implementation of the Basel III Accord, expected shortfall (ES) has gained increasing attention from regulators as a complement to value-at-risk (VaR). The problem of elicitability for ES makes jointly modeling VaR and ES a popular method to study ES. In this article, we develop model averaging for joint VaR and ES regression models that selects the two weight vectors by minimizing a jackknife criterion. We show the large sample properties of the estimators under potential model misspecification with increasing dimension of parameters and the asymptotic optimality of the selected weights in the sense of minimizing the out-of-sample excess final prediction error. Simulation studies and three empirical analyses reveal good finite sample performance.

Relatively, recent work by Jeganathan (2008, Cowles Foundation Discussion Paper 1649) and Wang (2014, Econometric Theory, 30(3), 509–535) on generalized martingale central limit theorems (MCLTs) implicitly introduces a new class of instrument arrays that yield (mixed) Gaussian limit theory irrespective of the persistence level in the data. Motivated by these developments, we propose a new semiparametric method for estimation and inference in nonlinear predictive regressions with persistent predictors. The proposed method that we term chronologically trimmed least squares (CTLS) is comparable to the IVX method of Phillips and Magdalinos (2009, Econometric inference in the vicinity of unity. Mimeo, Singapore Management University) and yields conventional inference in regressions where the nature and extent of persistence in the data are uncertain. In terms of model generality, our contribution to the existing literature is twofold. First, our covariate model space allows for both nearly integrated (NI) and fractional processes (stationary and nonstationary) as a special case, while the vast majority of articles in this area only consider NI arrays. Second, we allow for nonlinear regression functions. The CTLS estimator is obtained by applying certain chronological trimming to the OLS instruments using appropriate kernel functions of time trend variables. In particular, the instruments under consideration are a generalized (averaged) version of those widely used for time-varying parameter (TVP) models. For the purposes of our analysis, we develop a novel asymptotic theory for sample averages of various processes weighted by such kernel functionals which is of independent interest and highly relevant to the TVP literature. Leveraging our nonlinear framework, we also provide an investigation on the effects of misbalancing on the predictability hypothesis. A new methodology is proposed to mitigate misbalancing effects. These methods are used for exploring the predictability of SP500 returns.

Model selection (MS) and model averaging (MA) are two popular approaches when many candidate models exist. Theoretically, the estimation risk of an oracle MA is not larger than that of an oracle MS because the former is more flexible, but a foundational issue is this: Does MA offer a substantial improvement over MS? Recently, seminal work by Peng and Yang (2022) has answered this question under nested models with linear orthonormal series expansion. In the current paper, we further respond to this question under linear nested regression models. A more general nested framework, heteroscedastic and autocorrelated random errors, and sparse coefficients are allowed in the current paper, giving a scenario that is more common in practice. A remarkable implication is that MS can be significantly improved by MA under certain conditions. In addition, we further compare MA techniques with different weight sets. Simulation studies illustrate the theoretical findings in a variety of settings.

Recently, Kurisu and Otsu (2022b, Econometric Theory 38(1), 172–193) derived the uniform convergence rates for the nonparametric deconvolution estimators proposed by Li and Vuong (1998, Journal of Multivariate Analysis 65(2), 139–165). This article shows that faster uniform convergence rates can be established for their estimators under the same assumptions. In addition, a new class of deconvolution estimators based on a variant of Kotlarski’s identity is also proposed. It is shown that in some cases, these new estimators can have faster uniform convergence rates than the existing estimators.

We establish theoretical results about the low frequency contamination (i.e., long memory effects) induced by general nonstationarity for estimates such as the sample autocovariance and the periodogram, and deduce consequences for heteroskedasticity and autocorrelation robust (HAR) inference. We present explicit expressions for the asymptotic bias of these estimates. We show theoretically that nonparametric smoothing over time is robust to low frequency contamination. Nonstationarity can have consequences for both the size and power of HAR tests. Under the null hypothesis there are larger size distortions than when data are stationary. Under the alternative hypothesis, existing LRV estimators tend to be inflated and HAR tests can exhibit dramatic power losses. Our theory indicates that long bandwidths or fixed-b HAR tests suffer more from low frequency contamination relative to HAR tests based on HAC estimators, whereas recently introduced double kernel HAC estimators do not suffer from this problem. We present second-order Edgeworth expansions under nonstationarity about the distribution of HAC and DK-HAC estimators and about the corresponding t-test in the regression model. The results show that the distortions in the rejection rates can be induced by time variation in the second moments even when there is no break in the mean.