Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-05-01T14:09:59.691Z Has data issue: false hasContentIssue false
  • English
  • Français

The Relationship Between ϵ-Kronecker Sets and Sidon Sets

Published online by Cambridge University Press:  20 November 2018

Kathryn Hare  and
L. Thomas Ramsey
Kathryn Hare
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: [email protected]
L. Thomas Ramsey
Affiliation:
Dept. of Mathematics, University of Hawaii, Honolulu, HI 96822, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset $E$ of a discrete abelian group is called $\varepsilon$-Kronecker if all $E$-functions of modulus one can be approximated to within ϵ by characters. $E$ is called a Sidon set if all bounded $E$-functions can be interpolated by the Fourier transform of measures on the dual group. As $\varepsilon$-Kronecker sets with 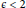$\varepsilon \,<\,2$ possess the same arithmetic properties as Sidon sets, it is natural to ask if they are Sidon. We use the Pisier net characterization of Sidonicity to prove this is true.

Keywords

43A4642A1542A55Kronecker setSidon set
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 521 - 527
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Galindo, J. and Hernandez, S., The concept of boundedness and the Bohr compactification of a MAP abelian group. Fund.Math.159(1999), no. 3, 195–218.Google Scholar
[2] Givens, B. N. and Kunen, K., Chromatic numbers and Bohr topologies. Topology Appl. 131(2003), no. 3, 189–202. http://dx.doi.org/10.1016/S0166-8641(02)00341-3 Google Scholar
[3] Graham, C. C. and Hare, K. E., e-Kronecker and IQ sets in abelian groups. I. Arithmetic properties of e-Kronecker sets. Math. Proc. Cambridge Philos. Soc. 140(2006), no. 3, 475–489. http://dx.doi.org/1 0.101 7/S0305004105009059 Google Scholar
[4] Graham, C. C. and Hare, K. E., Existence of large e-Kronecker and FZIQ sets in discrete abelian groups. Colloq. Math. 127(2012), no. 1, 1–15. http://dx.doi.org/10.4064/cm127-1-1 Google Scholar
[5] Graham, C. C. and Hare, K. E., Interpolation and Sidon sets for compact groups. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer, New York, 2013. http://dx.doi.org/10.1007/978-1-4614-5392-5 Google Scholar
[6] Graham, C. C. and Lau, A. T-M., Relative weak compactness of orbits in Banach spaces associated with locally compact groups. Trans. Amer. Math. Soc. 359(2007), no. 3,1129-1160. http://dx.doi.org/1 0.1090/S0002-9947-06-04039-6 Google Scholar
[7] Hare, K. E. and Ramsey, L. T., Kronecker constants of three element sets.Acta. Math.Hungar. 146(2015), no. 2, 306–331. http://dx.doi.org/10.1007/s10474-015-0529-2 Google Scholar
[8] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. Vol. II. Springer-Verlag, New York, 1970.Google Scholar
[9] Kahane, J-P., Algèbres tensoriellesetanalyseharmonique(d'après N. T. Varapoulos). Séminaire Bourbaki, 9, no. 291, Soc. Math. France, Paris, 1995, pp. 221–230.Google Scholar
[10] Kunen, K. and Rudin, W., Lacunarity and the Bohr topology.Math.Proc. Cambridge Philos. Soc. 126(1999), no. 1, 117–137. http://dx.doi.org/10.1017/S030500419800317X Google Scholar
[11] Li, D. and Queffelec, H., Introduction à l'étude des espaces de Banach. Analyse et probabilités. Cours Spécialisés, 12, Société Mathématique de France, Paris, 2004.Google Scholar
[12] Lopez, J. and Ross, K. A., Sidon sets. Lecture Notes in Pure and AppliedMathematics, 13, Marcel Dekker, New York, 1975.Google Scholar
[13] Pisier, G., Conditions d'entropie et caractérisations arithmétiques des ensembles de Sidon. In: Topics in modem harmonie analysis, Vol.I, II (Turin/Milan, 1982), 1st. Naz. Alta Mat. Francesco Severi, Rome, 1983, pp. 911–944.Google Scholar
[14] Varapoulos, N. Th., Tensor algebras and harmonie analysis. Acta Math. 119(1967), 51–112. http://dx.doi.org/10.1007/BF02392079 Google Scholar