We investigate the discrepancy between the distributions of the random variable 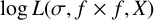 $\log L (\sigma , f \times f, X)$ and that of
$\log L (\sigma , f \times f, X)$ and that of 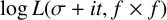 $\log L(\sigma +it, f \times f)$, that is,
$\log L(\sigma +it, f \times f)$, that is, 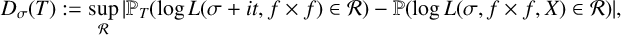 $$ \begin{align*} D_{\sigma} (T) := \sup_{\mathcal{R}} |\mathbb{P}_T(\log L(\sigma+it, f \times f) \in \mathcal{R}) - \mathbb{P}(\log L(\sigma, f \times f, X) \in \mathcal{R})|, \end{align*} $$
$$ \begin{align*} D_{\sigma} (T) := \sup_{\mathcal{R}} |\mathbb{P}_T(\log L(\sigma+it, f \times f) \in \mathcal{R}) - \mathbb{P}(\log L(\sigma, f \times f, X) \in \mathcal{R})|, \end{align*} $$
where the supremum is taken over rectangles 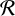 $\mathcal {R}$ with sides parallel to the coordinate axes. For fixed
$\mathcal {R}$ with sides parallel to the coordinate axes. For fixed 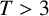 $T>3$ and
$T>3$ and 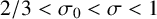 $2/3 <\sigma _0 < \sigma < 1$, we prove that
$2/3 <\sigma _0 < \sigma < 1$, we prove that 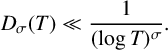 $$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}. \end{align*} $$
$$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}. \end{align*} $$
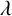 $\lambda $-QUIDDITIES OVER THE RINGS
$\lambda $-QUIDDITIES OVER THE RINGS 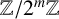 ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
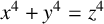 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 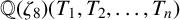 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
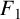 $F_1$
$F_1$