Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-05-02T18:58:39.981Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO QUESTIONS OF L. VAŠ ON $\ast $-CLEAN RINGS

Part of: Rings and algebras with additional structure Conditions on elements

Published online by Cambridge University Press:  08 March 2013

JIANLONG CHEN  and
JIAN CUI
JIANLONG CHEN
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, PR China email [email protected]
JIAN CUI*
Affiliation:
Department of Mathematics, Anhui Normal University, Wuhu 241000, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A $\ast $-ring 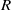$R$ is called (strongly) $\ast $-clean if every element of 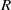$R$ is the sum of a unit and a projection (that commute). Vaš [‘$\ast $-Clean rings; some clean and almost clean Baer $\ast $-rings and von Neumann algebras’, J. Algebra 324(12) (2010), 3388–3400] asked whether there exists a $\ast $-ring that is clean but not $\ast $-clean and whether a unit regular and $\ast $-regular ring is strongly $\ast $-clean. In this paper, we answer these two questions. We also give some characterisations related to $\ast $-regular rings.

Keywords

∗-clean ringstrongly ∗-clean ring∗-regular ringstrongly clean ringunit regular ring

MSC classification

Secondary: 16U99: None of the above, but in this section 16W10: Rings with involution; Lie, Jordan and other nonassociative structures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 499 - 505
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Berberian, S. K., Baer ∗-Rings, Grundlehren der Mathematischen Wissenschaften, 195 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Camillo, V. P. and Khurana, D., ‘A characterization of unit regular rings’, Comm. Algebra 29 (5) (2001), 2293–2295.Google Scholar
Goodearl, K. R., Von Neumann Regular Rings, Monographs and Studies in Mathematics, 4 (Pitman, London, 1979).Google Scholar
Nicholson, W. K., ‘Lifting idempotents and exchange rings’, Trans. Amer. Math. Soc. 229 (1977), 269–278.CrossRefGoogle Scholar
Nicholson, W. K., ‘Strongly clean rings and Fitting’s lemma’, Comm. Algebra 27 (8) (1999), 3583–3592.CrossRefGoogle Scholar
Vaš, L., ‘$\ast $-Clean rings; some clean and almost clean Baer $\ast $-rings and von Neumann algebras’, J. Algebra 324 (12) (2010), 3388–3400.CrossRefGoogle Scholar