We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In a recent paper, topological spaces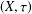 
$(X,{\it\tau})$ that are fragmented by a metric that generates the discrete topology were investigated. In the present paper we shall continue this investigation. In particular, we will show, among other things, that such spaces are 
${\it\sigma}$-scattered, that is, a countable union of scattered spaces, and characterise the continuous images of separable metrisable spaces by their fragmentability properties.
