We prove the existence of a family of slow-decay positive solutions of a supercritical elliptic equation with Hardy potential
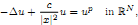
and study the stability and oscillation properties of these solutions. We also show that if the equation on ℝN has a stable slow-decay positive solution, then for any smooth compact K ⊂ ℝN a family of the exterior Dirichlet problems in ℝN \ K admits a continuum of stable slow-decay infinite-energy solutions.