We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
An A1−A∞ estimate, improving on a previous result for [b, TΩ] with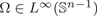 
$\Omega \in L^{infty}({\open S}^{n - 1})$ and b∈BMO is obtained. A new result in terms of the A∞ constant and the one supremum Aq−A∞exp constant is also proved, providing a counterpart for commutators of the result obtained by Li. Both of the preceding results rely upon a sparse domination result in terms of bilinear forms, which is established using techniques from Lerner.
