We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we prove a conditional principle of Gibbs type forrandom weighted measures of the form ${L_n=\frac{1}{n}\sum_{i=1}^nZ_i\delta_{x_i^n}}$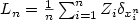 
, ((Zi)i being asequence of i.i.d. real random variables. Our work extends thepreceding results of Gamboa and Gassiat (1997), in allowing to consider thinconstraints. Transportation-like ideas are used in the proof.
