A linearly convergent iterative algorithm that approximates the rank-1 convex envelope $f^{rc}$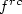 of a given function $f:\mathbb{R}^{n\times m} \to \mathbb{R}$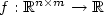, i.e. the largest function below f which is convex along all rank-1 lines, is established. The proposed algorithm is a modified version of an approximation scheme due to Dolzmann and Walkington.

The paper presents some results related to the optimal control approachs applying to inverse radiative transfer problems, to the theory of reflection operators, to the solvability of the inverse problems on boundary function and to algorithms for solution of these problems.