In this article we develop a test to determine whether a sextic polynomial that is irreducible over 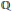 $\mathbb{Q}$ has Galois group isomorphic to the alternating group
$\mathbb{Q}$ has Galois group isomorphic to the alternating group 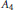 ${{A}_{4}}$. This test does not involve the computation of resolvents, and we use this test to construct several infinite families of such polynomials.
${{A}_{4}}$. This test does not involve the computation of resolvents, and we use this test to construct several infinite families of such polynomials.