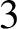 $3$
-manifolds
$3$
-manifolds
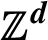 $\mathbb {Z}^d$
-actions: an ergodic theorem over rectangles with application to the critical dimensions
$\mathbb {Z}^d$
-actions: an ergodic theorem over rectangles with application to the critical dimensions