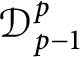 $\mathcal {D}^{p}_{p-1 }$
into tent spaces and Volterra operators
$\mathcal {D}^{p}_{p-1 }$
into tent spaces and Volterra operators
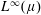 $L^{\infty }(\unicode[STIX]{x1D707})$
$L^{\infty }(\unicode[STIX]{x1D707})$
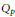 ${{Q}_{p}}$ Composition Operator
${{Q}_{p}}$ Composition Operator