We classify the automorphic Lie algebras of equivariant maps from a complex torus to 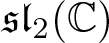 $\mathfrak{sl}_2(\mathbb{C})$. For each case, we compute a basis in a normal form. The automorphic Lie algebras correspond precisely to two disjoint families of Lie algebras parametrised by the modular curve of
$\mathfrak{sl}_2(\mathbb{C})$. For each case, we compute a basis in a normal form. The automorphic Lie algebras correspond precisely to two disjoint families of Lie algebras parametrised by the modular curve of 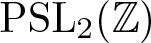 $\mathrm{PSL}_2({\mathbb{Z}})$, apart from four cases, which are all isomorphic to Onsager’s algebra.
$\mathrm{PSL}_2({\mathbb{Z}})$, apart from four cases, which are all isomorphic to Onsager’s algebra.