J.-C. Yoccoz proposed a natural extension of Selberg’s eigenvalue conjecture to moduli spaces of abelian differentials. We prove an approximation to this conjecture. This gives a qualitative generalization of Selberg’s 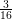 $\frac{3}{16}$ theorem to moduli spaces of abelian differentials on surfaces of genus
$\frac{3}{16}$ theorem to moduli spaces of abelian differentials on surfaces of genus 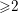 ${\geqslant}2$.
${\geqslant}2$.