In this article, we investigate the following non-linear Schrödinger (NLS) equation with Neumann boundary conditions: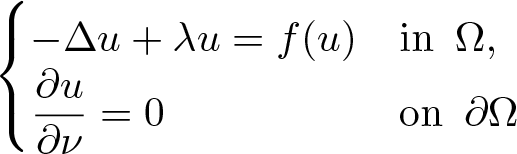

\begin{equation*}\begin{cases}-\Delta u+ \lambda u= f(u) & {\mathrm{in}} \,~ \Omega,\\\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega\end{cases}\end{equation*}

coupled with a constraint condition: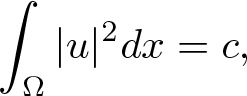

\begin{equation*}\int_{\Omega}|u|^2 dx=c,\end{equation*}

where 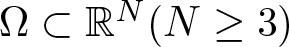$\Omega\subset \mathbb{R}^N(N\ge3)$ denotes a smooth bounded domain, ν represents the unit outer normal vector to 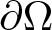$\partial \Omega$, c is a positive constant, and λ acts as a Lagrange multiplier. When the non-linearity f exhibits a general mass supercritical growth at infinity, we establish the existence of normalized solutions, which are not necessarily positive solutions and can be characterized as mountain pass type critical points of the associated constraint functional. Our approach provides a uniform treatment of various non-linearities, including cases such as 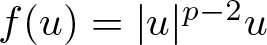$f(u)=|u|^{p-2}u$, 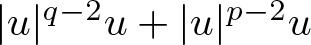$|u|^{q-2}u+ |u|^{p-2}u$, and 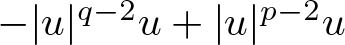$-|u|^{q-2}u+|u|^{p-2}u$, where 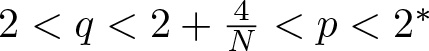$2 \lt q \lt 2+\frac{4}{N} \lt p \lt 2^*$. The result is obtained through a combination of a minimax principle with Morse index information for constrained functionals and a novel blow-up analysis for the NLS equation under Neumann boundary conditions.

We give a weak-Lp Serrin-type regularity criterion for a weak solution to the three-dimensional magnetohydrodynamics equations in a bounded domain Ω ⊂ ℝ3.

The pullback asymptotic behavior of the solutions for 2D Nonau-tonomous G-Navier-Stokes equations is studied, and the existence of its L2-pullback attractors on some bounded domains with Dirichlet boundary conditions is investigated by using the measure of noncompactness. Then the estimation of the fractal dimensions for the 2D G-Navier-Stokes equations is given.