Let 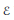 $\mathcal{E}$ be an ample vector bundle of rank
$\mathcal{E}$ be an ample vector bundle of rank  $r$ on a projective variety
$r$ on a projective variety 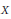 $X$ with only log-terminal singularities. We consider the nefness of adjoint divisors
$X$ with only log-terminal singularities. We consider the nefness of adjoint divisors 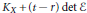 ${{K}_{X}}\,+\,\left( t-r \right)\,\det \,\mathcal{E}$ when
${{K}_{X}}\,+\,\left( t-r \right)\,\det \,\mathcal{E}$ when 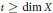 $t\,\ge \,\dim\,X$ and
$t\,\ge \,\dim\,X$ and 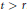 $t\,>\,r$. As an application, we classify pairs
$t\,>\,r$. As an application, we classify pairs 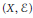 $\left( X,\,\mathcal{E} \right)$ with
$\left( X,\,\mathcal{E} \right)$ with  ${{c}_{r}}$-sectional genus zero.
${{c}_{r}}$-sectional genus zero.