In this paper we prove that decomposable forms, or homogeneous polynomials 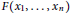 $F\left( {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right)$ with integer coefficients that split completely into linear factors over
$F\left( {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right)$ with integer coefficients that split completely into linear factors over 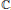 $\mathbb{C}$, take on infinitely many square-free values subject to simple necessary conditions, and they have
$\mathbb{C}$, take on infinitely many square-free values subject to simple necessary conditions, and they have 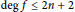 $\text{deg}\,f\,\le \,2n\,+\mid 2$ for all irreducible factors
$\text{deg}\,f\,\le \,2n\,+\mid 2$ for all irreducible factors 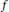 $f$ of
$f$ of  $F$. This work generalizes a theorem of Greaves.
$F$. This work generalizes a theorem of Greaves.