We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we completely solve the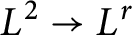 
$L^{2}\to L^{r}$
extension conjecture for the zero radius sphere over finite fields. We also obtain the sharp 
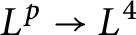$L^{p}\to L^{4}$
extension estimate for non-zero radii spheres over finite fields, which improves the previous result of the first and second authors significantly.
