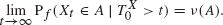We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let (Xt) be a one-dimensional Ornstein-Uhlenbeck process with initial density function f : ℝ+ → ℝ+, which is a regularly varying function with exponent -(1 + η), η ∊ (0,1). We prove the existence of a probability measure ν with a Lebesgue density, depending on η, such that for every A ∊ B(R+):
