We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The conditional expectation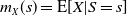 
$m_{X}(s)=\mathrm{E}[X|S=s]$, where X and Y are two independent random variables with 
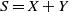$S=X+Y$, plays a key role in various actuarial applications. For instance, considering the conditional mean risk-sharing rule, 
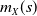$m_X(s)$ determines the contribution of the agent holding the risk X to a risk-sharing pool. It is also a relevant function in the context of risk management, for example, when considering natural capital allocation principles. The monotonicity of 
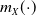$m_X(\!\cdot\!)$ is particularly significant under these frameworks, and it has been linked to log-concave densities since Efron (1965). However, the log-concavity assumption may not be realistic in some applications because it excludes heavy-tailed distributions. We consider random variables with regularly varying densities to illustrate how heavy tails can lead to a nonmonotonic behavior for 
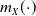$m_X(\!\cdot\!)$. This paper first aims to identify situations where 
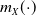$m_X(\!\cdot\!)$ could fail to be increasing according to the tail heaviness of X and Y. Second, the paper aims to study the asymptotic behavior of 
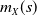$m_X(s)$ as the value s of the sum gets large. The analysis is then extended to zero-augmented probability distributions, commonly encountered in applications to insurance, and to sums of more than two random variables and to two random variables with a Farlie–Gumbel–Morgenstern copula. Consequences for risk sharing and capital allocation are discussed. Many numerical examples illustrate the results.
Entropy functionals of probability densities feature importantly in classifying certain finite-state stationary stochastic processes, in discriminating among competing hypotheses, in characterizing Gaussian, Poisson, and other densities, in describing information processes, and in other contexts. Two general types of problems are considered. For a given parametric family of densities 
the member of maximal (or sometimes minimal) entropy is ascertained. Secondly, we determine a natural (partial) ordering over 
for which the entropy functional is monotone. The examples include the multiparameter binomial, multiparameter negative binomial, some classes of log concave densities, and others.
