We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We compute the large size limit of the moment formula derived in [14] for the Hermitian Jacobi process at fixed time. Our computations rely on the polynomial division algorithm which allows to obtain cancellations similar to those obtained in [3, Lemma 3]. In particular, we identify the terms contributing to the limit and show they satisfy a double recurrence relation. We also determine explicitly some of them and revisit a special case relying on Carlitz summation identity for terminating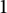 
$1$-balanced 
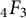${}_4F_3$ functions taken at unity.
