A convex body R in the hyperbolic plane is called reduced if any convex body 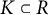$K\subset R$ has a smaller minimal width than R. We answer a few of Lassak’s questions about ordinary reduced polygons regarding its perimeter, diameter, and circumradius, and we also obtain a hyperbolic extension of a result of Fabińska.

We prove completeness of preferential conditional logic with respect to convexity over finite sets of points in the Euclidean plane. A conditional is defined to be true in a finite set of points if all extreme points of the set interpreting the antecedent satisfy the consequent. Equivalently, a conditional is true if the antecedent is contained in the convex hull of the points that satisfy both the antecedent and consequent. Our result is then that every consistent formula without nested conditionals is satisfiable in a model based on a finite set of points in the plane. The proof relies on a result by Richter and Rogers showing that every finite abstract convex geometry can be represented by convex polygons in the plane.

In this paper we investigate the asymptotic behavior of sequences of successive Steiner and Minkowski symmetrizations. We state an equivalence result between the convergences of those sequences for Minkowski and Steiner symmetrizations. Moreover, in the case of independent (and not necessarily identically distributed) directions, we prove the almost-sure convergence of successive symmetrizations at exponential rate for Minkowski, and at rate with c > 0 for Steiner.