Under sufficiently strong assumptions about the first term in an arithmetic progression, we prove that for any integer  $a$, there are infinitely many
$a$, there are infinitely many 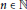 $n\,\in \,\mathbb{N}$ such that for each prime factor
$n\,\in \,\mathbb{N}$ such that for each prime factor 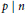 $p\,\text{ }\!\!|\!\!\text{ }\,n$, we have
$p\,\text{ }\!\!|\!\!\text{ }\,n$, we have 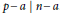 $p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers
$p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers  $n$ such that
$n$ such that 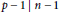 $p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every
$p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every 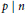 $p\,\text{ }\!\!|\!\!\text{ }\,n$.
$p\,\text{ }\!\!|\!\!\text{ }\,n$.
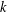 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE