Let 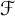 $\mathcal {F}$ denote the set of functions
$\mathcal {F}$ denote the set of functions 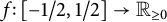 $f \colon [-1/2,1/2] \to \mathbb {R}_{\geq 0}$ such that
$f \colon [-1/2,1/2] \to \mathbb {R}_{\geq 0}$ such that 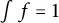 $\int f = 1$. We determine the value of
$\int f = 1$. We determine the value of 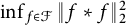 $\inf _{f \in \mathcal {F}} \| f \ast f \|_2^2$ up to a
$\inf _{f \in \mathcal {F}} \| f \ast f \|_2^2$ up to a 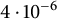 $4 \cdot 10^{-6}$ error, thereby making progress on a problem asked by Ben Green. Furthermore, we prove that a unique minimizer exists. As a corollary, we obtain improvements on the maximum size of
$4 \cdot 10^{-6}$ error, thereby making progress on a problem asked by Ben Green. Furthermore, we prove that a unique minimizer exists. As a corollary, we obtain improvements on the maximum size of 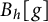 $B_h[g]$ sets for
$B_h[g]$ sets for 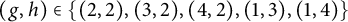 $(g,h) \in \{ (2,2),(3,2),(4,2),(1,3),(1,4)\}$.
$(g,h) \in \{ (2,2),(3,2),(4,2),(1,3),(1,4)\}$.
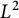 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality