We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A field F satisfies n-linkage on a subset of Ḟ if whenever the quaternion algebras
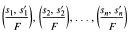
are equal in Br(F) there exist z ∈ Ḟ with
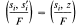
for i = 1, 2, . . ., n. This linkage of quaternion algebras is examined and its relationship to the torsion freeness of I2(F) and to the strong approximation property is investigated.
