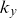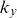1. Introduction
The confinement of plasmas in magnetically confined fusion experiments, such as tokamaks and stellarators, is dictated by small-scale microturbulence fluctuations. The turbulence produces anomalous transport of particles and heat, determining the background equilibrium profiles of density and temperature. In the past decades, we have improved our understanding of microturbulence fluctuations and their related anomalous transport using experimental measurements (Liewer Reference Liewer1985; Tynan, Fujisawa & McKee Reference Tynan, Fujisawa and McKee2009), analytical calculations of the micro-instabilities driving the turbulence (Horton Reference Horton1999; Garbet Reference Garbet2001), and using direct numerical turbulence simulations (Garbet et al. Reference Garbet, Idomura, Villard and Watanabe2010) and reduced fluid models (Staebler, Kinsey & Waltz Reference Staebler, Kinsey and Waltz2005; Ivanov et al. Reference Ivanov, Schekochihin, Dorl, Field and Parra2020). To study turbulence in magnetic confinement fusion devices, the theory of gyrokinetics (Catto Reference Catto1978; Frieman & Chen Reference Frieman and Chen1982) has been developed. Gyrokinetics has been highly successful at predicting the linear micro-instabilities driving turbulence and the associated transport. Due to the complexity of the equations, only linear calculations are analytically tractable in certain limits, but these cannot predict the saturated turbulence. To systematically study the turbulence saturated state and transport, the nonlinear gyrokinetic system of equations (Frieman & Chen Reference Frieman and Chen1982) has been implemented over the years in performance codes such as GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000), GS2 (Kotschenreuther Reference Kotschenreuther1995), GYRO (Candy & Waltz Reference Candy and Waltz2003 Reference Candy and Waltza ; Candy & Belli Reference Candy and Belli2014), CGYRO (Candy, Belli & Bravenec Reference Candy, Belli and Bravenec2016), STELLA (Barnes, Parra & Landreman Reference Barnes, Parra and Landreman2019) etc. These codes have been well benchmarked (Dimits et al., Reference Dimits2000; Nevins et al. Reference Nevins2006; Bravenec et al. Reference Bravenec, Chen, Candy, Wan and Parker2013) and have proven successful at predicting the experimentally inferred transport levels (Candy & Waltz, Reference Candy and Waltz2003 Reference Candy and Waltzb ; Howard et al. Reference Howard, White, Reinke, Greenwald, Holl, Candy and Walk2013).
Gyrokinetic codes can also calculate intrinsic turbulence characteristics, some of which can be measured by fluctuation diagnostics. Detailed comparisons of the intrinsic turbulence characteristics (fluctuation spectrum, correlation length, etc.) between the measurements and simulations remain difficult, but are becoming more common practice (White et al. Reference White2008; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012; Holland et al. Reference Holland2012; Leerink et al. Reference Leerink2012; Gusakov et al. Reference Gusakov2013; Stroth et al. Reference Stroth2015; Lechte et al. Reference Lechte, Conway, Goerler and Troester-Schmid2017; Happel et al. Reference Happel2017; Ruiz et al. Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith, Loureiro, Holland and Domier2019; Krutkin et al., Reference Krutkin2019 Reference Krutkina ). As we approach burning-plasma scenarios in the coming decade (ITER, Ikeda Reference Ikeda2007; SPARC, Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; STEP, Wilson et al. Reference Wilson, Chapman, Denton, Morris, Patel, Voss and Waldon2020), it is important to measure and characterise detailed physical turbulence processes in today’s tokamaks to validate our models and to build confidence in the model’s predictions for next generation fusion devices (Terry et al. Reference Terry2008; Greenwald Reference Greenwald2010; Holland Reference Holland2016; White Reference White2019). This motivates a detailed understanding of the complex turbulent phenomena being measured, as well as the detailed physical mechanisms in the measurement process itself. Both should be understood from a fundamental level.
To make quantitative comparisons between fluctuation diagnostics and numerical turbulence simulations, synthetic diagnostics are needed. Synthetic diagnostics enable the understanding of the diagnostic effects on the measurement (Bravenec & Nevins Reference Bravenec and Nevins2006; Shafer et al. Reference Shafer, Fonck, McKee and Schlossberg2006) and are a natural tool to help design new fluctuation diagnostics. These require a detailed understanding of the physical process behind the experimental measurement: collisional excitation and charge exchange rates in the case of beam emission spectroscopy (BES) (Fonck, Duperrex & Paul Reference Fonck, Duperrex and Paul1990; Hutchinson Reference Hutchinson2002), electron cyclotron emission (ECE) physics in the case of ECE (Sattler, Hartfuss & Team Reference Sattler, Hartfuss and Team1994; Cima et al. Reference Cima, Bravenec, Wootton, Rempel, Gandy, Watts and Kwon1995), plasma sheath physics for magnetic probe measurements (Hutchinson Reference Hutchinson2002), wave diffraction physics in phase-contrast imaging (Weisen Reference Weisen1988; Coda & Porkolab Reference Coda and Porkolab1992), and microwave scattering physics in the case of microwave diagnostics such as reflectometry (Cripwell et al. Reference Cripwell, Costley, Hubbard, Segre, Knoepfel and Sindoni1989; Costley et al. Reference Costley, Cripwell, Prentice and Sips1990), Doppler backscattering (DBS) (Holzhauer et al. Reference Holzhauer, Hirsch, Grossmann, Brañas and Serra1998; Hirsch et al. Reference Hirsch, Holzhauer, Baldzuhn and Kurzan2001) and high-k scattering (Mazzucato Reference Mazzucato1976; Surko & Slusher Reference Surko and Slusher1976; Slusher & Surko Reference Slusher and Surko1980; Peebles et al. Reference Peebles, N.C., Mase, Park and Semet1981), to name a few. In this manuscript, we focus on the measurement of the turbulence wavenumber spectrum via DBS. We use a linear-response beam-tracing model for the propagation and scattering of the microwaves inside the plasma to assess the impact of the beam properties on the backscattered power spectrum measured by DBS.
The Doppler backscattering technique (Holzhauer et al. Reference Holzhauer, Hirsch, Grossmann, Brañas and Serra1998; Hirsch et al. Reference Hirsch, Holzhauer, Baldzuhn and Kurzan2001) can measure the turbulent wavenumber spectrum (Hennequin et al. Reference Hennequin, Honoré, Truc, Quéméneur, Fenzi-Bonizec, Bourdelle, Garbet and Hoang2006; Hillesheim et al. Reference Hillesheim, Crocker, Peebles, Meyer, Meakins, Field, Dunai, Carr and Hawkes2015), zonal and equilibrium flows (Hirsch & Holzhauer Reference Hirsch and Holzhauer2004; Hennequin et al. Reference Hennequin, Honoré, Truc, Quéméneur, Lemoine, Chareau and Sabot2004; Hillesheim et al. Reference Hillesheim, Delabie, Meyer, Maggi, Meneses and Poli2016) as well as the turbulent correlation length (Schirmer et al. Reference Schirmer, Conway, Holzhauer, W. and Zohm2007). To perform the measurement, a beam of microwaves is launched into the core plasma with a finite incidence angle
![]() $\alpha _0$
with respect to the density gradient
$\alpha _0$
with respect to the density gradient
![]() $\nabla n$
. The beam propagates in the plasma until it encounters a cutoff surface, following which the forward beam is deviated away from the detector. The detector receives backscattered radiation from all along the beam path from turbulent fluctuations with characteristic wavevector
$\nabla n$
. The beam propagates in the plasma until it encounters a cutoff surface, following which the forward beam is deviated away from the detector. The detector receives backscattered radiation from all along the beam path from turbulent fluctuations with characteristic wavevector
![]() $\mathbf {k}$
, which are related to the incident beam wavevector
$\mathbf {k}$
, which are related to the incident beam wavevector
![]() $\mathbf {K}$
via the Bragg condition for backscattering
$\mathbf {K}$
via the Bragg condition for backscattering
![]() $\mathbf {k} = - 2 \mathbf {K}$
. Despite the simple qualitative idea behind the measurement, there is very rich physics impacting the scattering measurement, such as scattering along the path (Gusakov & Surkov Reference Gusakov and Surkov2004), the mismatch angle between the incident beam
$\mathbf {k} = - 2 \mathbf {K}$
. Despite the simple qualitative idea behind the measurement, there is very rich physics impacting the scattering measurement, such as scattering along the path (Gusakov & Surkov Reference Gusakov and Surkov2004), the mismatch angle between the incident beam
![]() $\mathbf {K}$
and the turbulence wavenumber
$\mathbf {K}$
and the turbulence wavenumber
![]() $\mathbf {k}$
(Rhodes et al. Reference Rhodes, Peebles, Nguyen, VanZeeland, deGrassie, Doyle, Wang and Zeng2006; Hillesheim et al. Reference Hillesheim, Crocker, Peebles, Meyer, Meakins, Field, Dunai, Carr and Hawkes2015; Hall-Chen et al. Reference Hall-Chen2022
Reference Hall-Chena
,
Reference Hall-Chen, Parra and Hillesheimb
,
Reference Hall-Chenc
), the Doppler shift, and a nonlinear response of the diagnostic for sufficiently large fluctuations (Gusakov, Surkov & Popov Reference Gusakov, Surkov and Popov2005; Blanco & Estrada Reference Blanco and Estrada2013; Fernández-Marina et al. Reference Fernández-Marina, Estrada and Blanco2014; Krutkin et al. Reference Krutkin, Gusakov, Heuraux and Lechte2019
Reference Krutkin, Gusakov, Heuraux and Lechteb
). One option to understand some of these effects is to couple high-fidelity full-wave models with direct nonlinear gyrokinetic simulations. This is a daunting task, but has been successfully carried out by some authors in the context of DBS (Stroth et al. Reference Stroth2015; Happel et al. Reference Happel2017; Lechte et al. Reference Lechte, Conway, Goerler and Troester-Schmid2017, Reference Lechte, Conway, Goerler and Happel2020). This critical and necessary exercise validates full-physics turbulence simulations as well as full-wave codes, where agreement should be reached between the full-physics modelling and experimental measurements. When agreement is not reached, the difference might be due to insufficient physics or resolution in the simulated turbulence, full-wave simulations or both. These exercises make it difficult to isolate particular physics phenomena affecting the measurement, which hinders fundamental understanding. A second option to understand DBS is to split the problem into smaller pieces and to use reduced models for the turbulence, the wave propagation or both. With reduced models, one can make analytical progress, have a strong handle on the hypotheses and limitations and establish a clear origin of the results and predictions. The latter is the approach we have opted for in this manuscript.
$\mathbf {k}$
(Rhodes et al. Reference Rhodes, Peebles, Nguyen, VanZeeland, deGrassie, Doyle, Wang and Zeng2006; Hillesheim et al. Reference Hillesheim, Crocker, Peebles, Meyer, Meakins, Field, Dunai, Carr and Hawkes2015; Hall-Chen et al. Reference Hall-Chen2022
Reference Hall-Chena
,
Reference Hall-Chen, Parra and Hillesheimb
,
Reference Hall-Chenc
), the Doppler shift, and a nonlinear response of the diagnostic for sufficiently large fluctuations (Gusakov, Surkov & Popov Reference Gusakov, Surkov and Popov2005; Blanco & Estrada Reference Blanco and Estrada2013; Fernández-Marina et al. Reference Fernández-Marina, Estrada and Blanco2014; Krutkin et al. Reference Krutkin, Gusakov, Heuraux and Lechte2019
Reference Krutkin, Gusakov, Heuraux and Lechteb
). One option to understand some of these effects is to couple high-fidelity full-wave models with direct nonlinear gyrokinetic simulations. This is a daunting task, but has been successfully carried out by some authors in the context of DBS (Stroth et al. Reference Stroth2015; Happel et al. Reference Happel2017; Lechte et al. Reference Lechte, Conway, Goerler and Troester-Schmid2017, Reference Lechte, Conway, Goerler and Happel2020). This critical and necessary exercise validates full-physics turbulence simulations as well as full-wave codes, where agreement should be reached between the full-physics modelling and experimental measurements. When agreement is not reached, the difference might be due to insufficient physics or resolution in the simulated turbulence, full-wave simulations or both. These exercises make it difficult to isolate particular physics phenomena affecting the measurement, which hinders fundamental understanding. A second option to understand DBS is to split the problem into smaller pieces and to use reduced models for the turbulence, the wave propagation or both. With reduced models, one can make analytical progress, have a strong handle on the hypotheses and limitations and establish a clear origin of the results and predictions. The latter is the approach we have opted for in this manuscript.
First-principles theory and analytical calculations of the DBS scattered power spectra have been carried out for almost two decades by Gusakov et al. (Gusakov & Surkov Reference Gusakov and Surkov2004; Gusakov & Popov Reference Gusakov and Popov2011; Gusakov et al. Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). These calculations start from the full-wave analytical solution to the Helmholtz wave equation, and they are restricted to two-dimensional (2-D) geometry in a Cartesian slab, although some preliminary calculations have been performed in a cylinder (Gusakov & Krutkin Reference Gusakov and Krutkin2017). In their work, Gusakov et al. argue that non-local ‘forward-scattering’ events cause an enhancement of the DBS signal preferentially for decreasing incidence angles
![]() $\alpha _0$
. Gusakov et al. also analysed the measurement locality, challenging the traditional understanding that DBS is sensitive to fluctuations from the cutoff (in this manuscript, we will interchangeably refer to this location as the cutoff, or turning point). These calculations use a realistic representation of the wave scattering process and a simple turbulence spectrum (Gaussian) in their analytical calculations.
$\alpha _0$
. Gusakov et al. also analysed the measurement locality, challenging the traditional understanding that DBS is sensitive to fluctuations from the cutoff (in this manuscript, we will interchangeably refer to this location as the cutoff, or turning point). These calculations use a realistic representation of the wave scattering process and a simple turbulence spectrum (Gaussian) in their analytical calculations.
In this work, we adopt Gaussian beam tracing to model the propagation of the electric field in a simple 2-D slab geometry, as used previously (Gusakov & Surkov Reference Gusakov and Surkov2004; Gusakov & Popov Reference Gusakov and Popov2011; Gusakov et al. Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). The theory of Gaussian beam-tracing has been developed in different fields of physics (Casperson Reference Casperson1973; Červený et al. Reference Červený, Popov and Pšenčík1982; Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007). In magnetic confinement fusion, the theory of Gaussian beam propagation in anisotropic media has been used for approximately three decades (Pereverzev Reference Pereverzev1992, Reference Pereverzev1993, Reference Pereverzev1996, Reference Pereverzev1998; Poli, Pereverzev & Peeters Reference Poli, Pereverzev and Peeters1999, Reference Poli, Peeters and Pereverzev2001
Reference Poli, Peeters and Pereverzevb
,Reference Poli, Pereverzev, Peeters and Bornaticic) and has been successfully implemented in numerical codes such as TORBEAM (Poli et al. Reference Poli, Peeters and Pereverzev2001
Reference Poli, Peeters and Pereverzeva
,Reference Poli2018) and more recently in Scotty (Hall-Chen et al. Reference Hall-Chen and Hill2025) to model reflectometry/DBS and electron cyclotron (EC) beam absorption. The Gaussian beam-tracing equations are a set of ordinary differential equations (ODEs), which present great computational advantage with respect to full-wave codes, even in two dimensions. Although scarce, analytic solutions for beam-tracing exist (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010; Weber, Maj & Poli Reference Weber, Maj and Poli2018) and are exploited in this work. Previous authors have shown that the Gaussian beam-tracing model remains a good approximation when the incidence angle
![]() $\alpha _0$
is not too small (Balakin et al. Reference Balakin, Balakina, Permitin and Smirnov2007, Reference Balakin, Balakina and Westerhof2008; Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). Gaussian beam tracing is bound to break near the cutoff at small angles (
$\alpha _0$
is not too small (Balakin et al. Reference Balakin, Balakina, Permitin and Smirnov2007, Reference Balakin, Balakina and Westerhof2008; Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). Gaussian beam tracing is bound to break near the cutoff at small angles (
![]() $\alpha _0 \sim 10^{\circ }$
for
$\alpha _0 \sim 10^{\circ }$
for
![]() $K_0L$
values of approximately
$K_0L$
values of approximately
![]() $ 10^3$
characteristic of magnetic confinement experiments (Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025)). For these small angles, beam tracing could yield inaccurate predictions for a small part of the beam and the resulting scattering. Some of the concerns are revisited in this manuscript.
$ 10^3$
characteristic of magnetic confinement experiments (Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025)). For these small angles, beam tracing could yield inaccurate predictions for a small part of the beam and the resulting scattering. Some of the concerns are revisited in this manuscript.
The rest of the manuscript proceeds as follows. In § 2, we introduce Gaussian beam tracing. We use the analytical solution by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010) that exhibits beam focusing (also referred to as pinching or lensing) near the turning point. This phenomenon of beam focusing was already observed in past work using numerical simulations (Poli et al. Reference Poli, Pereverzev and Peeters1999, Reference Poli, Pereverzev, Peeters and Bornatici2001
Reference Poli, Pereverzev, Peeters and Bornaticic
; Yu. A. Kravtsov and Berczynski P., Reference Kravtsov and Berczynski2007; Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007). We characterise how an O-mode beam focuses in a 2-D Cartesian slab with a linear density profile as a function of the beam initial conditions. In § 3, we use the analytic solution for beam tracing in conjunction with a recently developed linear-response beam model of DBS (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) to find an analytic expression for the DBS filter function
![]() $|F_{x\mu }|^2$
. With this filter function, we develop and implement an analytic synthetic diagnostic for DBS, which can be used to analyse fluctuation data from gyrokinetic codes. In § 4, we show that by parametrising the filter function
$|F_{x\mu }|^2$
. With this filter function, we develop and implement an analytic synthetic diagnostic for DBS, which can be used to analyse fluctuation data from gyrokinetic codes. In § 4, we show that by parametrising the filter function
![]() $|F_{x\mu }|^2$
by the scattered radial wavenumber component
$|F_{x\mu }|^2$
by the scattered radial wavenumber component
![]() $k_x$
of the turbulent wavevector along the path, we are able to recover previous known results for the scattered power (Gusakov & Surkov Reference Gusakov and Surkov2004; Gusakov et al. Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Our results confirm that the results by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) can be obtained using the Gaussian beam-tracing approximation, and hence, do not include full-wave effects. Gusakov et al. argued that the enhancement of the DBS signal power was due to a forward-scattering component, which is absent in our model by design. We find the exact same analytical formulae as Gusakov et al. for the DBS filter function
$k_x$
of the turbulent wavevector along the path, we are able to recover previous known results for the scattered power (Gusakov & Surkov Reference Gusakov and Surkov2004; Gusakov et al. Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Our results confirm that the results by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) can be obtained using the Gaussian beam-tracing approximation, and hence, do not include full-wave effects. Gusakov et al. argued that the enhancement of the DBS signal power was due to a forward-scattering component, which is absent in our model by design. We find the exact same analytical formulae as Gusakov et al. for the DBS filter function
![]() $|F_{x\mu }|^2$
by using a model only based on backscattering and Gaussian beam tracing, instead of the full-wave solution. This suggests that forward scattering, in the form described by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017), is not the physical phenomenon leading to the enhancement of the DBS power for finite
$|F_{x\mu }|^2$
by using a model only based on backscattering and Gaussian beam tracing, instead of the full-wave solution. This suggests that forward scattering, in the form described by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017), is not the physical phenomenon leading to the enhancement of the DBS power for finite
![]() $k_x$
values near the turning point, but rather that beam focusing is. Section 4, in conjunction with Appendices C and D, establishes the equivalence between the beam model of DBS by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model by Gusakov et al. In the last section of this manuscript, we apply the analytical filter function
$k_x$
values near the turning point, but rather that beam focusing is. Section 4, in conjunction with Appendices C and D, establishes the equivalence between the beam model of DBS by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model by Gusakov et al. In the last section of this manuscript, we apply the analytical filter function
![]() $|F_{x\mu }|^2$
from the beam model to understand its effect on scattered power measurements from DBS. We use a realistic turbulence spectrum obtained from gyrokinetic simulations, following recent work by Ruiz et al. (Reference Ruiz2022). Our model predicts that, for a representative NSTX-inspired example, the Doppler-backscattered power spectrum cannot reproduce the peak in
$|F_{x\mu }|^2$
from the beam model to understand its effect on scattered power measurements from DBS. We use a realistic turbulence spectrum obtained from gyrokinetic simulations, following recent work by Ruiz et al. (Reference Ruiz2022). Our model predicts that, for a representative NSTX-inspired example, the Doppler-backscattered power spectrum cannot reproduce the peak in
![]() $k_y$
from the true density-fluctuation spectrum, but is accurate at predicting the characteristic spectral exponent of the turbulent cascade.
$k_y$
from the true density-fluctuation spectrum, but is accurate at predicting the characteristic spectral exponent of the turbulent cascade.
2. Beam focusing and beam tracing
In DBS experiments, one can model the propagation of the microwaves launched externally from the plasma as a Gaussian beam. The behaviour of a Gaussian beam can be complex due to the inhomogeneities in density and magnetic field. To gain physical understanding of the phenomena affecting beam propagation, we first discuss vacuum propagation.
In vacuum, a Gaussian beam will propagate in a straight line. If the beam is not focusing, then it will constantly expand. Asymptotically, the width of the beam will grow linearly with the propagation path length. If the beam is initially focusing, it will focus to a minimum width, called the waist, following which the beam will expand, as previously described by Goldsmith (Reference Goldsmith1998). This behaviour is due to diffraction: a wave packet of finite extent does not want to be confined: if initially expanding, it will not cease to expand; if initially focusing, it will focus before expanding.
For a beam propagating in an anisotropic, inhomogeneous medium, its trajectory can substantially differ from that in vacuum. The inhomogeneity in space causes refraction of the central ray. The inhomogeneity experienced by the central ray causes changes in the group velocity
![]() $\mathbf {g}$
, which affects the intensity of the electric field, which scales as
$\mathbf {g}$
, which affects the intensity of the electric field, which scales as
![]() $E \propto 1/|\mathbf {g}|^{\frac {1}{2}}$
(Lopez & Dodin Reference Lopez and Dodin2021).Footnote
1
Of particular interest is the problem of a wave encountering a cutoff surface at normal incidence. This is the situation encountered by diagnostics such as reflectometry, where the group velocity along the inhomogeneity approaches zero at the cutoff and the electric field diverges. This is a well-known limitation of beam tracing when close to normal incidence to the inhomogeneity. Close to a turning point, one cannot assume slow variation of the background experienced by the wave and the beam-tracing approximation fails. To solve this problem, one needs to resort to solving the full Helmholtz wave equation. This limitation disappears when the angle of incidence with respect to the inhomogeneity is finite (or more precisely, large enough, as we will discuss), such as encountered in DBS. The group velocity still decreases approaching the cutoff (the component of
$E \propto 1/|\mathbf {g}|^{\frac {1}{2}}$
(Lopez & Dodin Reference Lopez and Dodin2021).Footnote
1
Of particular interest is the problem of a wave encountering a cutoff surface at normal incidence. This is the situation encountered by diagnostics such as reflectometry, where the group velocity along the inhomogeneity approaches zero at the cutoff and the electric field diverges. This is a well-known limitation of beam tracing when close to normal incidence to the inhomogeneity. Close to a turning point, one cannot assume slow variation of the background experienced by the wave and the beam-tracing approximation fails. To solve this problem, one needs to resort to solving the full Helmholtz wave equation. This limitation disappears when the angle of incidence with respect to the inhomogeneity is finite (or more precisely, large enough, as we will discuss), such as encountered in DBS. The group velocity still decreases approaching the cutoff (the component of
![]() $\mathbf {g}$
along the inhomogeneity vanishes, while the
$\mathbf {g}$
along the inhomogeneity vanishes, while the
![]() $\mathbf {g}$
component perpendicular to it remains approximately constant). This produces an enhancement of the electric field
$\mathbf {g}$
component perpendicular to it remains approximately constant). This produces an enhancement of the electric field
![]() $E$
near the turning point, which should remain finite due to a finite
$E$
near the turning point, which should remain finite due to a finite
![]() $|\mathbf {g}|$
. The decrease of the group velocity near the turning point is one factor that enhances the electric-field amplitude in DBS and will be discussed in this manuscript. This will show up as a ray term affecting the filter function
$|\mathbf {g}|$
. The decrease of the group velocity near the turning point is one factor that enhances the electric-field amplitude in DBS and will be discussed in this manuscript. This will show up as a ray term affecting the filter function
![]() $|F_{x\mu }|^2$
for backscattering. As we will see,
$|F_{x\mu }|^2$
for backscattering. As we will see,
![]() $|F_{x\mu }|^2 \propto 1/|\mathbf {g}| \propto 1/K$
. Importantly, there is another factor that can enhance the intensity of the electric field and that is the beam width.
$|F_{x\mu }|^2 \propto 1/|\mathbf {g}| \propto 1/K$
. Importantly, there is another factor that can enhance the intensity of the electric field and that is the beam width.
For a beam propagating in an anisotropic, inhomogeneous medium, the behaviour of the beam width can also be substantially different from the behaviour in vacuum. Beam tracing can describe diffraction effects due to the finite extent
![]() $\sim W$
of a wave packet in the direction transverse to the direction of propagation. In addition to the beam waist present in vacuum, other authors have shown that the beam can experience additional focusing, or lensing, in the presence of inhomogeneity (Poli et al. Reference Poli, Pereverzev and Peeters1999, Reference Poli, Pereverzev, Peeters and Bornatici2001
Reference Poli, Pereverzev, Peeters and Bornaticic
; Bornatici & Maj Reference Bornatici and Maj2003; Maj Reference Maj2005; Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007; Berczyński et al. Reference Berczyński, Kravtsov and Żeglinski2008; Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). This phenomenon tends to happen close to the turning point. In the beam-tracing formulation, one can show that the electric-field amplitude
$\sim W$
of a wave packet in the direction transverse to the direction of propagation. In addition to the beam waist present in vacuum, other authors have shown that the beam can experience additional focusing, or lensing, in the presence of inhomogeneity (Poli et al. Reference Poli, Pereverzev and Peeters1999, Reference Poli, Pereverzev, Peeters and Bornatici2001
Reference Poli, Pereverzev, Peeters and Bornaticic
; Bornatici & Maj Reference Bornatici and Maj2003; Maj Reference Maj2005; Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007; Berczyński et al. Reference Berczyński, Kravtsov and Żeglinski2008; Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). This phenomenon tends to happen close to the turning point. In the beam-tracing formulation, one can show that the electric-field amplitude
![]() $E$
scales inversely proportional to the beam width
$E$
scales inversely proportional to the beam width
![]() $W$
, as
$W$
, as
![]() $E \propto 1/W^{\frac {1}{2}}$
(Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
).Footnote
2
This shows that when the beam focuses, the electric field is enhanced. This is a different effect from the enhancement due to the decreasing group velocity of the central ray. In fact, it can be shown that the electric field scales as
$E \propto 1/W^{\frac {1}{2}}$
(Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
).Footnote
2
This shows that when the beam focuses, the electric field is enhanced. This is a different effect from the enhancement due to the decreasing group velocity of the central ray. In fact, it can be shown that the electric field scales as
![]() $E \propto 1/(|\mathbf {g}|W)^{\frac {1}{2}}$
(Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). It is this phenomenon, the beam focusing in an inhomogeneous medium, that we explore in this manuscript. In full toroidal geometry, this results in the filter function
$E \propto 1/(|\mathbf {g}|W)^{\frac {1}{2}}$
(Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). It is this phenomenon, the beam focusing in an inhomogeneous medium, that we explore in this manuscript. In full toroidal geometry, this results in the filter function
![]() $\propto 1/|\mathbf {g}|W \propto 1/KW$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
).Footnote
3
In the 2-D linear-layer model, we will find
$\propto 1/|\mathbf {g}|W \propto 1/KW$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
).Footnote
3
In the 2-D linear-layer model, we will find
![]() $\mathbf {g} = 2 \mathbf {K}/K_0^2$
and
$\mathbf {g} = 2 \mathbf {K}/K_0^2$
and
![]() $|F_{x\mu }|^2/|F_0|^2 = K_0W_0/KW$
, where
$|F_{x\mu }|^2/|F_0|^2 = K_0W_0/KW$
, where
![]() $|F_0|^2$
,
$|F_0|^2$
,
![]() $K_0$
and
$K_0$
and
![]() $W_0$
are the filter function
$W_0$
are the filter function
![]() $|F_{x\mu }|^2$
, the magnitude of the beam central wavenumber
$|F_{x\mu }|^2$
, the magnitude of the beam central wavenumber
![]() $\mathbf {K}$
and the beam width
$\mathbf {K}$
and the beam width
![]() $W$
evaluated at the initial condition. We call the
$W$
evaluated at the initial condition. We call the
![]() $1/W$
term the beam term in the filter function (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). Importantly, the beam term and the ray term can both separately contribute to the enhancement of the electric field in the vicinity of a turning point. This motivates studying the propagation of a ray and a beam in inhomogeneous, anisotropic media. For this, we adopt the ray-tracing and beam-tracing formulation, which we describe next.
$1/W$
term the beam term in the filter function (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). Importantly, the beam term and the ray term can both separately contribute to the enhancement of the electric field in the vicinity of a turning point. This motivates studying the propagation of a ray and a beam in inhomogeneous, anisotropic media. For this, we adopt the ray-tracing and beam-tracing formulation, which we describe next.
2.1. Ray tracing and Gaussian beam tracing
This section closely follows notation introduced by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ), who rederived Gaussian beam tracing from first principles and presented it in full detail.
The beam-tracing method (or paraxial WKB) is an asymptotic representation of the electric field in anisotropic media for finite size wave packets with characteristic scale in the transverse direction of propagation
![]() $\sim W$
. Beam tracing extends ray tracing by including diffraction effects in a set of ODEs. As in ray tracing, the wavevector of the wave
$\sim W$
. Beam tracing extends ray tracing by including diffraction effects in a set of ODEs. As in ray tracing, the wavevector of the wave
![]() $\mathbf {K}$
is ordered inversely proportional to the wavelength
$\mathbf {K}$
is ordered inversely proportional to the wavelength
![]() $\sim 1/\lambda$
, while the background equilibrium is assumed to vary on a scale
$\sim 1/\lambda$
, while the background equilibrium is assumed to vary on a scale
![]() $L \gg \lambda$
. In beam tracing, the scale
$L \gg \lambda$
. In beam tracing, the scale
![]() $W$
is intermediate and obeys
$W$
is intermediate and obeys
![]() $L \gg W \gg \lambda$
, with
$L \gg W \gg \lambda$
, with
![]() $W \sim (\lambda L)^{\frac {1}{2}}$
. In this manuscript, we denote the wavevector associated with the wave with the capital letter
$W \sim (\lambda L)^{\frac {1}{2}}$
. In this manuscript, we denote the wavevector associated with the wave with the capital letter
![]() $\mathbf {K}$
. The same notation will apply to its components
$\mathbf {K}$
. The same notation will apply to its components
![]() $K_g$
,
$K_g$
,
![]() $K_x$
, etc., while the wavevector components associated with the turbulence will be in lower case, e.g.
$K_x$
, etc., while the wavevector components associated with the turbulence will be in lower case, e.g.
![]() $k_x$
and
$k_x$
and
![]() $k_y$
.
$k_y$
.
In Gaussian beam tracing, the variation of the wave electric field perpendicular to a central ray is assumed to be of Gaussian shape. The central ray propagation obeys the traditional ray-tracing equations for the ray position vector
![]() $\mathbf {q}(\tau ) \sim L$
and wavevector
$\mathbf {q}(\tau ) \sim L$
and wavevector
![]() $\mathbf {K}(\tau ) \sim 1/\lambda$
, where
$\mathbf {K}(\tau ) \sim 1/\lambda$
, where
![]() $\tau$
is a parameter along the central ray. For reference, the ray-tracing equations are
$\tau$
is a parameter along the central ray. For reference, the ray-tracing equations are
 \begin{align} \begin{alignedat}{2} & \frac {\text {d}\mathbf {q}}{\text {d}\tau } = \nabla _K H, \\ & \frac {\text {d}\mathbf {K}}{\text {d}\tau } = - \nabla H, \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\text {d}\mathbf {q}}{\text {d}\tau } = \nabla _K H, \\ & \frac {\text {d}\mathbf {K}}{\text {d}\tau } = - \nabla H, \end{alignedat} \end{align}
where
![]() $H$
is the cold-plasma dispersion relation and
$H$
is the cold-plasma dispersion relation and
![]() $\mathbf {g} = \nabla _K H$
is the effective group velocity. Note that there are infinite ways to define an
$\mathbf {g} = \nabla _K H$
is the effective group velocity. Note that there are infinite ways to define an
![]() $H$
that give rise to the same
$H$
that give rise to the same
![]() $\mathbf {q}$
and
$\mathbf {q}$
and
![]() $\mathbf {K}$
(the different definitions of
$\mathbf {K}$
(the different definitions of
![]() $H$
only change the dummy parameter
$H$
only change the dummy parameter
![]() $\tau$
). We use a specific definition that ensures that the wave electric field scales as
$\tau$
). We use a specific definition that ensures that the wave electric field scales as
![]() $\sim 1/g^{\frac {1}{2}}$
, where
$\sim 1/g^{\frac {1}{2}}$
, where
![]() $\mathbf {g} = \text {d} \mathbf {q}/\text {d}\tau$
(see discussion in § 2.2 of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) for details). Equations (2.1) are routinely solved by codes such as GENRAY (Smirnov et al. Reference Smirnov2009).
$\mathbf {g} = \text {d} \mathbf {q}/\text {d}\tau$
(see discussion in § 2.2 of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) for details). Equations (2.1) are routinely solved by codes such as GENRAY (Smirnov et al. Reference Smirnov2009).
In the Gaussian beam-tracing approximation, the beam electric field
![]() $\mathbf {E}_b$
is written in amplitude and phase as
$\mathbf {E}_b$
is written in amplitude and phase as
![]() $\mathbf {E}_b(\mathbf {r}) = \mathbf {A}(\mathbf {r}) \exp [i \psi (\mathbf {r})] +$
c.c., where the phase
$\mathbf {E}_b(\mathbf {r}) = \mathbf {A}(\mathbf {r}) \exp [i \psi (\mathbf {r})] +$
c.c., where the phase
![]() $\psi$
is expanded to second order about the central ray in the perpendicular direction to
$\psi$
is expanded to second order about the central ray in the perpendicular direction to
![]() $\mathbf {g}$
,
$\mathbf {g}$
,
Here,
![]() $s = s(\tau ) = \int ^\tau {\mathbf {K}(\tau ^{\prime}) \cdot \mathbf {g} (\tau ^{\prime})} \ \text {d}\tau ^{\prime} = \int ^\tau {{K}_g g } \ \text {d}\tau ^{\prime}$
is the large phase Eikonal term measuring the variation of the electric field along the central ray. The phase given by
$s = s(\tau ) = \int ^\tau {\mathbf {K}(\tau ^{\prime}) \cdot \mathbf {g} (\tau ^{\prime})} \ \text {d}\tau ^{\prime} = \int ^\tau {{K}_g g } \ \text {d}\tau ^{\prime}$
is the large phase Eikonal term measuring the variation of the electric field along the central ray. The phase given by
![]() $s$
scales as
$s$
scales as
![]() $s \sim L/\lambda \gg 1$
, which follows from
$s \sim L/\lambda \gg 1$
, which follows from
![]() $\tau \sim L/\lambda$
,
$\tau \sim L/\lambda$
,
![]() $g \sim \lambda$
and
$g \sim \lambda$
and
![]() $H \sim 1$
(see (2.1)). Note that the second term in (2.2) is ordered as
$H \sim 1$
(see (2.1)). Note that the second term in (2.2) is ordered as
![]() $\mathbf {K}_w \cdot \mathbf {w} \sim W/\lambda \gg 1$
, while the last term is
$\mathbf {K}_w \cdot \mathbf {w} \sim W/\lambda \gg 1$
, while the last term is
![]() $(1/2) \mathbf {w} \cdot \boldsymbol{\unicode{x1D6F9}\!}_w \cdot \mathbf {w} \sim 1$
, since the components of
$(1/2) \mathbf {w} \cdot \boldsymbol{\unicode{x1D6F9}\!}_w \cdot \mathbf {w} \sim 1$
, since the components of
![]() $\boldsymbol{\unicode{x1D6F9}\!}_w$
are ordered as
$\boldsymbol{\unicode{x1D6F9}\!}_w$
are ordered as
![]() $\Psi _{w,ij} \sim 1/W^2$
. The vector
$\Psi _{w,ij} \sim 1/W^2$
. The vector
![]() $\mathbf {K}_w = (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} ) \cdot \mathbf {K}$
in the phase (2.2) is the component of
$\mathbf {K}_w = (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} ) \cdot \mathbf {K}$
in the phase (2.2) is the component of
![]() $\mathbf {K}$
perpendicular to
$\mathbf {K}$
perpendicular to
![]() ${\hat{\mathbf{g}}}$
. The matrix
${\hat{\mathbf{g}}}$
. The matrix
![]() $\boldsymbol{\unicode{x1D6F9}\!}_w$
is a singular
$\boldsymbol{\unicode{x1D6F9}\!}_w$
is a singular
![]() $3 \times 3$
matrix and only has non-zero components along the two directions perpendicular to
$3 \times 3$
matrix and only has non-zero components along the two directions perpendicular to
![]() ${\hat{\mathbf{g}}}$
. The matrix
${\hat{\mathbf{g}}}$
. The matrix
![]() $\boldsymbol{\unicode{x1D6F9}\!}_w$
contains information about the phase-front curvature of the Gaussian beam (through the non-zero eigenvalues of its real part =
$\boldsymbol{\unicode{x1D6F9}\!}_w$
contains information about the phase-front curvature of the Gaussian beam (through the non-zero eigenvalues of its real part =
![]() ${K^3}/{(K_g^2 R_{b,i})}$
, where
${K^3}/{(K_g^2 R_{b,i})}$
, where
![]() $K = |\mathbf {K}|$
and
$K = |\mathbf {K}|$
and
![]() $K_g = \mathbf {K} \cdot {\hat{\mathbf{g}}}$
) and beam width
$K_g = \mathbf {K} \cdot {\hat{\mathbf{g}}}$
) and beam width
![]() $W_i$
(through the non-zero eigenvalues of its imaginary part
$W_i$
(through the non-zero eigenvalues of its imaginary part
![]() $ = {2}/{W_i^2}$
).
$ = {2}/{W_i^2}$
).

Figure 1. Lab frame and beam frame for coordinates with oblique beam incidence (finite
![]() $\alpha _0$
) used throughout this manuscript. Here,
$\alpha _0$
) used throughout this manuscript. Here,
![]() $(x_c, y_c)$
denote the coordinates of a point along the central ray and not the cutoff location.
$(x_c, y_c)$
denote the coordinates of a point along the central ray and not the cutoff location.
A general point in space is described by
We define the (orthonormal) beam-frame coordinate system
![]() $\{ {\hat{\mathbf{Y}}}, {\hat{\mathbf{g}}}, {\hat{\mathbf{X}}} \}$
as follows:
$\{ {\hat{\mathbf{Y}}}, {\hat{\mathbf{g}}}, {\hat{\mathbf{X}}} \}$
as follows:
where
![]() ${\hat{\mathbf{b}}} = \mathbf {B}/B$
is the unit vector along the background magnetic field. This is not to be confused with the Cartesian lab-frame system of coordinates
${\hat{\mathbf{b}}} = \mathbf {B}/B$
is the unit vector along the background magnetic field. This is not to be confused with the Cartesian lab-frame system of coordinates
![]() $ \{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(see figure 1 for a comparison between beam frame and lab frame in two dimensions). Using (2.3) and (2.4), a general point in space can be determined from the coordinate
$ \{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(see figure 1 for a comparison between beam frame and lab frame in two dimensions). Using (2.3) and (2.4), a general point in space can be determined from the coordinate
![]() $\tau$
along the central ray and the two coordinates
$\tau$
along the central ray and the two coordinates
![]() $X$
and
$X$
and
![]() $Y$
in the directions perpendicular to
$Y$
in the directions perpendicular to
![]() ${\hat{\mathbf{g}}}$
.
${\hat{\mathbf{g}}}$
.
In the beam-tracing formulation which we use in this manuscript, the beam-tracing matrix
![]() $\boldsymbol{\unicode{x1D6F9}}$
is a
$\boldsymbol{\unicode{x1D6F9}}$
is a
![]() $3 \times 3$
matrix that is convenient to evolve along the central ray. From this matrix, we can obtain
$3 \times 3$
matrix that is convenient to evolve along the central ray. From this matrix, we can obtain
![]() $\boldsymbol{\unicode{x1D6F9}\!}_w$
by projection
$\boldsymbol{\unicode{x1D6F9}\!}_w$
by projection
![]() $\boldsymbol{\unicode{x1D6F9}\!}_w = (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} ) \cdot \boldsymbol{\unicode{x1D6F9}} \cdot (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} )$
. The beam matrix
$\boldsymbol{\unicode{x1D6F9}\!}_w = (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} ) \cdot \boldsymbol{\unicode{x1D6F9}} \cdot (\mathbf {I} - {\hat{\mathbf{g}}} {\hat{\mathbf{g}}} )$
. The beam matrix
![]() $\boldsymbol{\unicode{x1D6F9}}$
follows the beam-tracing evolution equations, a set of ordinary differential equations parametrised by
$\boldsymbol{\unicode{x1D6F9}}$
follows the beam-tracing evolution equations, a set of ordinary differential equations parametrised by
![]() $\tau$
, see Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and Appendix A. Given
$\tau$
, see Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and Appendix A. Given
![]() $\boldsymbol{\unicode{x1D6F9}}$
, the electric field
$\boldsymbol{\unicode{x1D6F9}}$
, the electric field
![]() $\mathbf {E}_b$
in Gaussian beam tracing is written as
$\mathbf {E}_b$
in Gaussian beam tracing is written as
 \begin{align} \begin{alignedat}{2} & \mathbf {E}_b = &&A_{ant}\exp [{i(\phi _G+\phi _P)}] \bigg [ \frac { \det (\Im [\boldsymbol{\unicode{x1D6F9}\!}_w]) }{ \det (\Im [\boldsymbol{\unicode{x1D6F9}}_{w,ant}]) } \bigg ]^{\frac {1}{4}} \bigg ( {\frac {g_{ant} }{g}} \bigg )^{\frac {1}{2}} \\ & && \times \exp \Big ( is + i \mathbf {K}_w\cdot \mathbf {w} + \frac {i}{2} \mathbf {w} \cdot \boldsymbol{\unicode{x1D6F9}\!}_w \cdot \mathbf {w} \Big ) {\hat{\mathbf{e}}} \ + \ c.c., \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \mathbf {E}_b = &&A_{ant}\exp [{i(\phi _G+\phi _P)}] \bigg [ \frac { \det (\Im [\boldsymbol{\unicode{x1D6F9}\!}_w]) }{ \det (\Im [\boldsymbol{\unicode{x1D6F9}}_{w,ant}]) } \bigg ]^{\frac {1}{4}} \bigg ( {\frac {g_{ant} }{g}} \bigg )^{\frac {1}{2}} \\ & && \times \exp \Big ( is + i \mathbf {K}_w\cdot \mathbf {w} + \frac {i}{2} \mathbf {w} \cdot \boldsymbol{\unicode{x1D6F9}\!}_w \cdot \mathbf {w} \Big ) {\hat{\mathbf{e}}} \ + \ c.c., \end{alignedat} \end{align}
where
![]() $\mathbf {E}_b = E_b {\hat{\mathbf{e}}}$
and
$\mathbf {E}_b = E_b {\hat{\mathbf{e}}}$
and
![]() $\Im$
denotes the imaginary part. The unit vector
$\Im$
denotes the imaginary part. The unit vector
![]() ${\hat{\mathbf{e}}}$
is the polarisation vector,
${\hat{\mathbf{e}}}$
is the polarisation vector,
![]() $\phi _P$
and
$\phi _P$
and
![]() $\phi _G$
are respectively the polarisation and Gouy phases, which are of limited interest in this manuscript (see Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) for their evolution equations). The subscript
$\phi _G$
are respectively the polarisation and Gouy phases, which are of limited interest in this manuscript (see Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) for their evolution equations). The subscript
![]() $(.)_{ant}$
means that quantities are evaluated at the antenna launch location. As previously discussed, the prescription in (2.5) for the electric field shows that
$(.)_{ant}$
means that quantities are evaluated at the antenna launch location. As previously discussed, the prescription in (2.5) for the electric field shows that
![]() $E_b \sim 1/(gW_X W_Y)^{\frac {1}{2}} \propto 1/(KW_X W_Y)^{\frac {1}{2}}$
. This is due to the terms
$E_b \sim 1/(gW_X W_Y)^{\frac {1}{2}} \propto 1/(KW_X W_Y)^{\frac {1}{2}}$
. This is due to the terms
![]() $\det (\Im [\boldsymbol{\unicode{x1D6F9}\!}_w])^{\frac {1}{4}} \propto 1/(W_X W_Y)^{\frac {1}{2}}$
and
$\det (\Im [\boldsymbol{\unicode{x1D6F9}\!}_w])^{\frac {1}{4}} \propto 1/(W_X W_Y)^{\frac {1}{2}}$
and
![]() $1/g^{\frac {1}{2}} \propto 1/K^{\frac {1}{2}}$
. For the purposes of this manuscript, in the 2-D linear layer, only the width
$1/g^{\frac {1}{2}} \propto 1/K^{\frac {1}{2}}$
. For the purposes of this manuscript, in the 2-D linear layer, only the width
![]() $W_Y$
in the direction
$W_Y$
in the direction
![]() $\hat {\mathbf {Y}}$
is relevant.
$\hat {\mathbf {Y}}$
is relevant.
In the next section, we show numerical solutions to the beam-tracing equations (Appendix A) in real tokamak geometry, which exhibit the phenomenon of beam focusing. These will be compared with analytical solutions to beam tracing for the 2-D linear-layer problem. We will see how the analytical solution qualitatively captures the phenomenon of beam focusing.

Figure 2. (a) Trajectory of the central ray of a DBS beam projected on the poloidal
![]() $(R,Z)$
plane overlaid by contour lines of the poloidal flux function
$(R,Z)$
plane overlaid by contour lines of the poloidal flux function
![]() $\Psi _p$
for JET discharge 97 080 (NBI-heated L-mode). (b) Numerical solution of the two principal widths perpendicular to the central ray propagation, noted here
$\Psi _p$
for JET discharge 97 080 (NBI-heated L-mode). (b) Numerical solution of the two principal widths perpendicular to the central ray propagation, noted here
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, using Scotty (Hall-Chen et al. Reference Hall-Chen and Hill2025). The black dots correspond to the turning point in the trajectory (vanishing wavenumber component normal to the flux surface), while the red dots correspond to the plasma exit. (c) Analytic solution of the beam-tracing equations for the 2-D linear layer in slab geometry using experimental parameters corresponding to the case shown in panels (a) and (b):
$W_2$
, using Scotty (Hall-Chen et al. Reference Hall-Chen and Hill2025). The black dots correspond to the turning point in the trajectory (vanishing wavenumber component normal to the flux surface), while the red dots correspond to the plasma exit. (c) Analytic solution of the beam-tracing equations for the 2-D linear layer in slab geometry using experimental parameters corresponding to the case shown in panels (a) and (b):
![]() $K_0L\approx 1600, K_0W_0\approx 22$
,
$K_0L\approx 1600, K_0W_0\approx 22$
,
![]() $\alpha _0 \approx 10^{\circ }$
,
$\alpha _0 \approx 10^{\circ }$
,
![]() $R_{Y0}=\infty$
(launch at the waist). There is good qualitative agreement between the numerical and analytic solutions.
$R_{Y0}=\infty$
(launch at the waist). There is good qualitative agreement between the numerical and analytic solutions.
2.2. Beam focusing in experimentally relevant conditions
In this section, we will show that the beam-focusing phenomenon appears in numerical calculations of beam-tracing modelling of DBS experiments. We will see that the beam width has a tendency to focus as the beam moves towards higher density. A beam propagating in increasing density is routinely encountered in most DBS measurements.
We describe the phenomenon of beam focusing, that is, the decrease or compression of the beam width as the beam propagates near the turning point that characterises a cutoff. This phenomenon was previously observed in numerical simulations (Poli et al. Reference Poli, Pereverzev and Peeters1999, Reference Poli, Pereverzev, Peeters and Bornatici2001
Reference Poli, Pereverzev, Peeters and Bornaticic
; Yu. A. Kravtsov and Berczynski P. Reference Kravtsov and Berczynski2007; Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007, Reference Conway, Lechte and Fochi2015, Reference Conway, Lechte, Poli and Maj2019) and in analytic solutions (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010; Weber et al. Reference Weber, Maj and Poli2018). To confirm the existence of the beam-focusing phenomenon and its relevance to real-life experimental conditions, in figure 2, we show the result of a numerical calculation with the Scotty code (Hall-Chen et al. Reference Hall-Chen and Hill2025) for the DBS beam propagation with X-mode polarisation in the core of the tokamak JET for L-mode discharge 97 080 in a phase heated only by neutral-beam injection (NBI). Figure 2(a) shows the trajectory of the central ray projected on the 2-D
![]() $(R,Z)$
plane overlaid by contour lines of the poloidal flux function
$(R,Z)$
plane overlaid by contour lines of the poloidal flux function
![]() $\Psi _p$
. The turning point is at
$\Psi _p$
. The turning point is at
![]() $\Psi _p/\Psi _{p0} \approx 0.7$
, where
$\Psi _p/\Psi _{p0} \approx 0.7$
, where
![]() $\Psi _{p0}$
is the separatrix value. Figure 2(b) shows the perpendicular widths
$\Psi _{p0}$
is the separatrix value. Figure 2(b) shows the perpendicular widths
![]() $W_1$
and
$W_1$
and
![]() $W_2$
that correspond to the non-zero eigenvalues of the imaginary part of the beam-tracing matrix
$W_2$
that correspond to the non-zero eigenvalues of the imaginary part of the beam-tracing matrix
![]() $\Im [ \boldsymbol{\unicode{x1D6F9}\!}_w ]$
. We approximate the overmoded waveguide launch by a beam with circular cross-section and initial conditions
$\Im [ \boldsymbol{\unicode{x1D6F9}\!}_w ]$
. We approximate the overmoded waveguide launch by a beam with circular cross-section and initial conditions
![]() $W_0 \approx 1$
cm,
$W_0 \approx 1$
cm,
![]() $R_{Y0} = \infty$
(launch at the waist). The widths
$R_{Y0} = \infty$
(launch at the waist). The widths
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are plotted against the path length
$W_2$
are plotted against the path length
![]() $l = \int \text {d}\tau g$
. The beam propagates in vacuum from
$l = \int \text {d}\tau g$
. The beam propagates in vacuum from
![]() $l \approx 0$
to
$l \approx 0$
to
![]() $l \approx 0.4$
m, which roughly corresponds to the plasma edge. In vacuum, both principal beam widths follow the same behaviour: expansion following a launch from the waist. In the plasma, both widths initially continue expanding, but one of them (blue) starts contracting and reaching a minimum at
$l \approx 0.4$
m, which roughly corresponds to the plasma edge. In vacuum, both principal beam widths follow the same behaviour: expansion following a launch from the waist. In the plasma, both widths initially continue expanding, but one of them (blue) starts contracting and reaching a minimum at
![]() $l \approx 0.7$
m (beam focusing). Following the beam focusing, the contracted width starts to expand again. The behaviour observed in figure 2(b) consistently appears in beam-tracing numerical calculations near a turning point, and is confirmed by the beam-tracing code TORBEAM (Poli et al. Reference Poli, Peeters and Pereverzev2001
Reference Poli, Peeters and Pereverzeva
, Reference Poli2018) (not shown). This behaviour was also observed in simulations of DBS in other tokamaks (Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007, Reference Conway, Lechte and Fochi2015, Reference Conway, Lechte, Poli and Maj2019). This motivates studying the beam-focusing phenomenon using a reduced model that is analytically tractable, the 2-D linear-layer model (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010), which we present next.
$l \approx 0.7$
m (beam focusing). Following the beam focusing, the contracted width starts to expand again. The behaviour observed in figure 2(b) consistently appears in beam-tracing numerical calculations near a turning point, and is confirmed by the beam-tracing code TORBEAM (Poli et al. Reference Poli, Peeters and Pereverzev2001
Reference Poli, Peeters and Pereverzeva
, Reference Poli2018) (not shown). This behaviour was also observed in simulations of DBS in other tokamaks (Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007, Reference Conway, Lechte and Fochi2015, Reference Conway, Lechte, Poli and Maj2019). This motivates studying the beam-focusing phenomenon using a reduced model that is analytically tractable, the 2-D linear-layer model (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010), which we present next.
2.3. Beam focusing in the 2-D linear layer
To understand the beam-focusing phenomenon observed in the Scotty numerical solution in toroidal geometry in figure 2 (b), we first solve the equations for ray tracing (2.1) using a simplified Cartesian-slab geometry in two dimensions (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). Following the ray-tracing solution, we will subsequently solve the beam-tracing equations.
We solve the 2-D linear-layer model in the lab frame, given by the unit vectors
![]() $\{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(figure 1). Using (2.4), the lab-frame unit vectors are related to the beam-frame
$\{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(figure 1). Using (2.4), the lab-frame unit vectors are related to the beam-frame
![]() $\{ {\hat{\mathbf{Y}}}, {\hat{\mathbf{g}}}, {\hat{\mathbf{X}}} \}$
in two dimensions by a simple rotation
$\{ {\hat{\mathbf{Y}}}, {\hat{\mathbf{g}}}, {\hat{\mathbf{X}}} \}$
in two dimensions by a simple rotation
 \begin{align} \begin{alignedat}{2} &\hat {\mathbf {Y}} &&= \sin \alpha \ \hat {\mathbf {x}} - \cos \alpha \ \hat {\mathbf {y}} , \\ & \hat {\mathbf {g}} &&= \cos \alpha \ \hat {\mathbf {x}} + \sin \alpha \ \hat {\mathbf {y}} , \\ &\hat {\mathbf {X}} &&= \hat {\mathbf {z}}, \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} &\hat {\mathbf {Y}} &&= \sin \alpha \ \hat {\mathbf {x}} - \cos \alpha \ \hat {\mathbf {y}} , \\ & \hat {\mathbf {g}} &&= \cos \alpha \ \hat {\mathbf {x}} + \sin \alpha \ \hat {\mathbf {y}} , \\ &\hat {\mathbf {X}} &&= \hat {\mathbf {z}}, \end{alignedat} \end{align}
where we note that
![]() $\alpha = \alpha (\tau )$
is a function of
$\alpha = \alpha (\tau )$
is a function of
![]() $\tau$
. We will ignore the coordinate
$\tau$
. We will ignore the coordinate
![]() ${\hat{\mathbf{z}}}$
, which points in the antiparallel direction to the magnetic field. These definitions will be needed in order to subsequently solve the beam-tracing equations. The 2-D linear-layer problem in slab geometry has O-mode polarisation, uniform
${\hat{\mathbf{z}}}$
, which points in the antiparallel direction to the magnetic field. These definitions will be needed in order to subsequently solve the beam-tracing equations. The 2-D linear-layer problem in slab geometry has O-mode polarisation, uniform
![]() $\mathbf {B}(\mathbf {r}) = {B}_0 {\hat{\mathbf{b}}} = - B_0 {\hat{\mathbf{z}}}$
and linear density profile
$\mathbf {B}(\mathbf {r}) = {B}_0 {\hat{\mathbf{b}}} = - B_0 {\hat{\mathbf{z}}}$
and linear density profile
![]() $\omega _{pe}^2(x) = \Omega ^2 x/L$
. Here,
$\omega _{pe}^2(x) = \Omega ^2 x/L$
. Here,
![]() $x$
is our ’radial’ coordinate, also Cartesian
$x$
is our ’radial’ coordinate, also Cartesian
![]() $x$
in figure 1,
$x$
in figure 1,
![]() $\Omega$
is the launch frequency,
$\Omega$
is the launch frequency,
![]() $\omega _{pe0} = \Omega \cos \alpha _0$
is the electron plasma frequency at the turning point location,
$\omega _{pe0} = \Omega \cos \alpha _0$
is the electron plasma frequency at the turning point location,
![]() $L_n = L \cos ^2\alpha _0$
is the turning point locationFootnote
4
and
$L_n = L \cos ^2\alpha _0$
is the turning point locationFootnote
4
and
![]() $L$
is the turning point location for zero incident angle (
$L$
is the turning point location for zero incident angle (
![]() $\alpha _0=0$
, see figure 1). The ray-tracing equations determine the trajectory of the central ray
$\alpha _0=0$
, see figure 1). The ray-tracing equations determine the trajectory of the central ray
![]() $\mathbf {q}$
and the wavevector of the central ray
$\mathbf {q}$
and the wavevector of the central ray
![]() $\mathbf {K}$
. In the 2-D linear layer,
$\mathbf {K}$
. In the 2-D linear layer,
![]() $\mathbf {q}$
and
$\mathbf {q}$
and
![]() $\mathbf {K}$
have components
$\mathbf {K}$
have components
 \begin{align} \begin{alignedat}{2} & \mathbf {q}(\tau ^{\prime}) &&= \big (x_c(\tau ^{\prime}), y_c (\tau ^{\prime}) \big ) , \\ &\mathbf {K}(\tau ^{\prime}) &&= \big (K_x(\tau ^{\prime}), K_y(\tau ^{\prime})\big ) , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \mathbf {q}(\tau ^{\prime}) &&= \big (x_c(\tau ^{\prime}), y_c (\tau ^{\prime}) \big ) , \\ &\mathbf {K}(\tau ^{\prime}) &&= \big (K_x(\tau ^{\prime}), K_y(\tau ^{\prime})\big ) , \end{alignedat} \end{align}
where
![]() $\tau ^{\prime} = \tau /K_0L$
is the normalised parameter along the path and
$\tau ^{\prime} = \tau /K_0L$
is the normalised parameter along the path and
![]() $K_0$
is the wavenumber magnitude at launch. Here,
$K_0$
is the wavenumber magnitude at launch. Here,
![]() $(x_c, y_c)$
denote the coordinates of an arbitrary point along the central ray and not the cutoff location. In this manuscript, we define the turning point, or cutoff, as the location where
$(x_c, y_c)$
denote the coordinates of an arbitrary point along the central ray and not the cutoff location. In this manuscript, we define the turning point, or cutoff, as the location where
![]() $K_x=0$
(
$K_x=0$
(
![]() $K_x$
is the Cartesian
$K_x$
is the Cartesian
![]() $x$
-component of the beam wavevector
$x$
-component of the beam wavevector
![]() ${\textbf{K}}$
, see (2.9)). We will make use of the dispersion relation
${\textbf{K}}$
, see (2.9)). We will make use of the dispersion relation
![]() $H=0$
, where
$H=0$
, where
![]() $H$
takes the form
$H$
takes the form
 \begin{align} \begin{aligned} H = \frac {K^2}{K_0^2} - 1 + \frac {\omega _{pe}^2}{\Omega ^2} \end{aligned} \end{align}
\begin{align} \begin{aligned} H = \frac {K^2}{K_0^2} - 1 + \frac {\omega _{pe}^2}{\Omega ^2} \end{aligned} \end{align}
for the O-mode. The form of
![]() $H$
given by (2.8) ensures that the electric field is given by (2.5). Using (2.8), we have
$H$
given by (2.8) ensures that the electric field is given by (2.5). Using (2.8), we have
![]() $\nabla _K H = \mathbf {g} = 2 \mathbf {K}/K_0^2$
(initial condition
$\nabla _K H = \mathbf {g} = 2 \mathbf {K}/K_0^2$
(initial condition
![]() $g_{ant} = 2/K_0$
) and
$g_{ant} = 2/K_0$
) and
![]() $\nabla H = {\hat{\mathbf{x}}}/L$
. As can be seen from figure 1, the magnetic field is into the page and the angle
$\nabla H = {\hat{\mathbf{x}}}/L$
. As can be seen from figure 1, the magnetic field is into the page and the angle
![]() $\alpha _0$
measures the vertical incidence angle of the central ray at launch. In what follows,
$\alpha _0$
measures the vertical incidence angle of the central ray at launch. In what follows,
![]() $\alpha$
will measure the vertical incidence angle along the central ray. The initial conditions are
$\alpha$
will measure the vertical incidence angle along the central ray. The initial conditions are
![]() $(x_{c}, y_{c})_0 = (0, y_0)$
,
$(x_{c}, y_{c})_0 = (0, y_0)$
,
![]() $(K_{x}, K_{y})_0 = K_0 ( \cos \alpha _0, \sin \alpha _0)$
. The ray-tracing (2.1) can be readily solved in the 2-D linear layer, giving the following components of
$(K_{x}, K_{y})_0 = K_0 ( \cos \alpha _0, \sin \alpha _0)$
. The ray-tracing (2.1) can be readily solved in the 2-D linear layer, giving the following components of
![]() $\mathbf {q}$
and
$\mathbf {q}$
and
![]() $\mathbf {K}$
in (2.7):
$\mathbf {K}$
in (2.7):
 \begin{align} \begin{aligned} & x_c(\tau ^{\prime}) = L \Big ( \cos ^2\alpha _0 - (\cos \alpha _0- {\tau ^{\prime}} )^2 \Big ) = L \big ( \cos ^2\alpha _0 - {K_x^2}/{K_0^2}\big ) , \\ & y_c(\tau ^{\prime}) = y_0 + 2 L \sin \alpha _0 \ \tau ^{\prime} , \\ & K_x(\tau ^{\prime}) = K_0 (\cos \alpha _0 - \tau ^{\prime}) = K_0 (\cos ^2\alpha _0 - x_c/L)^{\frac {1}{2}} , \\ & K_y(\tau ^{\prime}) = K_0\sin \alpha _0. & \end{aligned} \end{align}
\begin{align} \begin{aligned} & x_c(\tau ^{\prime}) = L \Big ( \cos ^2\alpha _0 - (\cos \alpha _0- {\tau ^{\prime}} )^2 \Big ) = L \big ( \cos ^2\alpha _0 - {K_x^2}/{K_0^2}\big ) , \\ & y_c(\tau ^{\prime}) = y_0 + 2 L \sin \alpha _0 \ \tau ^{\prime} , \\ & K_x(\tau ^{\prime}) = K_0 (\cos \alpha _0 - \tau ^{\prime}) = K_0 (\cos ^2\alpha _0 - x_c/L)^{\frac {1}{2}} , \\ & K_y(\tau ^{\prime}) = K_0\sin \alpha _0. & \end{aligned} \end{align}
Equations (2.9) describe a parabolic trajectory in
![]() $(x,y)$
. We will find it useful to parametrise the ray trajectory by the radial wavenumber of the central ray
$(x,y)$
. We will find it useful to parametrise the ray trajectory by the radial wavenumber of the central ray
![]() $K_x$
, instead of
$K_x$
, instead of
![]() $\tau$
. We will also parametrise the beam-tracing solution by
$\tau$
. We will also parametrise the beam-tracing solution by
![]() $K_x$
.
$K_x$
.
The 2-D linear-layer problem with finite incident angle
![]() $\alpha _0$
is also analytically solvable in Gaussian beam tracing, as was previously shown by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). For details of the derivation, we refer the reader to Appendix A. The beam-tracing equations for the linear-layer problem reduce to
$\alpha _0$
is also analytically solvable in Gaussian beam tracing, as was previously shown by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). For details of the derivation, we refer the reader to Appendix A. The beam-tracing equations for the linear-layer problem reduce to
![]() ${\text {d} \boldsymbol{\unicode{x1D6F9}}}/{ \text {d} \tau } = -({2}/{K_0^2}) \boldsymbol{\unicode{x1D6F9}}^2$
, which is a nonlinear matrix equation for
${\text {d} \boldsymbol{\unicode{x1D6F9}}}/{ \text {d} \tau } = -({2}/{K_0^2}) \boldsymbol{\unicode{x1D6F9}}^2$
, which is a nonlinear matrix equation for
![]() $\boldsymbol{\unicode{x1D6F9}}$
. This equation belongs to a class of ODEs known as Ricatti equations. The main component of the beam matrix
$\boldsymbol{\unicode{x1D6F9}}$
. This equation belongs to a class of ODEs known as Ricatti equations. The main component of the beam matrix
![]() $\boldsymbol{\unicode{x1D6F9}}$
of interest in this manuscript is the
$\boldsymbol{\unicode{x1D6F9}}$
of interest in this manuscript is the
![]() $\boldsymbol{\hat {Y}} \boldsymbol{\hat {Y}}$
component
$\boldsymbol{\hat {Y}} \boldsymbol{\hat {Y}}$
component
![]() $\Psi _{YY}$
, which captures the beam-focusing phenomenon through the perpendicular beam width
$\Psi _{YY}$
, which captures the beam-focusing phenomenon through the perpendicular beam width
![]() $W_Y = (2/\Im [\Psi _{YY}])^{\frac {1}{2}}$
. The solution for
$W_Y = (2/\Im [\Psi _{YY}])^{\frac {1}{2}}$
. The solution for
![]() $\Psi _{YY}$
is
$\Psi _{YY}$
is
 \begin{align} \begin{aligned} & \Psi _{YY}(K_x) &&= \frac { - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big [ \frac {K_x^3}{K_0^3} + 3 \sin ^2\alpha _0 \frac {K_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0}\big(\cos ^2\alpha _0 - \sin ^2\alpha _0 \big) \Big ] }{ \Big [ \sin ^2\alpha _0 + \frac {K_x^2}{K_0^2} \Big ] \Big [ \frac {K_x}{K_0} + 2 \Psi _{yy0}^{\prime} \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0 }{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \Big ) \Big ] } \frac {K_0}{L} , \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{YY}(K_x) &&= \frac { - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big [ \frac {K_x^3}{K_0^3} + 3 \sin ^2\alpha _0 \frac {K_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0}\big(\cos ^2\alpha _0 - \sin ^2\alpha _0 \big) \Big ] }{ \Big [ \sin ^2\alpha _0 + \frac {K_x^2}{K_0^2} \Big ] \Big [ \frac {K_x}{K_0} + 2 \Psi _{yy0}^{\prime} \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0 }{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \Big ) \Big ] } \frac {K_0}{L} , \end{aligned} \end{align}
where
![]() $\Psi _{yy0}^{\prime} = \Psi _{yy0} ({L}/{K_0})$
is the initial condition for the beam
$\Psi _{yy0}^{\prime} = \Psi _{yy0} ({L}/{K_0})$
is the initial condition for the beam
![]() $\Psi _{yy}$
component in the lab-frame direction
$\Psi _{yy}$
component in the lab-frame direction
![]() ${\hat{\mathbf{y}}}$
(vertical direction in figure 1) that contains information about the initial beam width and radius of curvature of the phase front (normalised to
${\hat{\mathbf{y}}}$
(vertical direction in figure 1) that contains information about the initial beam width and radius of curvature of the phase front (normalised to
![]() $K_0/L$
, see Appendix A for details). Equation (2.10) is the basis for most of the analysis in this manuscript. The reader is referred to Appendix A for details in the calculation of
$K_0/L$
, see Appendix A for details). Equation (2.10) is the basis for most of the analysis in this manuscript. The reader is referred to Appendix A for details in the calculation of
![]() $\Psi _{YY}$
. The analytic solution of
$\Psi _{YY}$
. The analytic solution of
![]() $\Psi _{YY}$
contains the beam-focusing phenomenon for the 2-D linear-layer problem and is used to characterise the Doppler backscattering power contributions along the beam trajectory through the filter function
$\Psi _{YY}$
contains the beam-focusing phenomenon for the 2-D linear-layer problem and is used to characterise the Doppler backscattering power contributions along the beam trajectory through the filter function
![]() $|F_{x\mu }|^2$
(§ 3).
$|F_{x\mu }|^2$
(§ 3).
We wish to compare the analytic beam-tracing solution for
![]() $W_{Y}$
, computed using (2.10), with the numerical solution in toroidal geometry shown in figures 2(a) and 2(b). To do so, we extract the physical values of
$W_{Y}$
, computed using (2.10), with the numerical solution in toroidal geometry shown in figures 2(a) and 2(b). To do so, we extract the physical values of
![]() $K_0$
,
$K_0$
,
![]() $L$
and the initial width
$L$
and the initial width
![]() $W_0$
from experimental conditions in the JET discharge 97080:
$W_0$
from experimental conditions in the JET discharge 97080:
![]() $K_0 \approx 2200$
m
$K_0 \approx 2200$
m
![]() $^{-1}$
,
$^{-1}$
,
![]() $W_0 \approx 1$
cm and
$W_0 \approx 1$
cm and
![]() $L\approx 0.7$
m. Knowing that, in reality, the beam propagates in a plasma with a varying density gradient, we choose the value of
$L\approx 0.7$
m. Knowing that, in reality, the beam propagates in a plasma with a varying density gradient, we choose the value of
![]() $L$
to be the average value of the density gradient experienced by the beam as it propagates through the plasma, yielding
$L$
to be the average value of the density gradient experienced by the beam as it propagates through the plasma, yielding
![]() $L \approx 0.7$
m. We use the experimental values of
$L \approx 0.7$
m. We use the experimental values of
![]() $K_0$
,
$K_0$
,
![]() $L$
and
$L$
and
![]() $W_0$
to normalise the initial conditions in the analytic beam-tracing solution, giving
$W_0$
to normalise the initial conditions in the analytic beam-tracing solution, giving
![]() $K_0W_0\approx 22$
,
$K_0W_0\approx 22$
,
![]() $K_0 L \approx 1600$
. The width
$K_0 L \approx 1600$
. The width
![]() $W_Y$
that is perpendicular to the central ray propagation and in the
$W_Y$
that is perpendicular to the central ray propagation and in the
![]() $(x,y)$
plane is plotted in blue in figure 2(c), as a function of the beam path length
$(x,y)$
plane is plotted in blue in figure 2(c), as a function of the beam path length
![]() $l$
. The vacuum solution is plotted in orange (absence of plasma),Footnote
5
which is also the same solution as the
$l$
. The vacuum solution is plotted in orange (absence of plasma),Footnote
5
which is also the same solution as the
![]() $\hat {\mathbf {z}}$
-component of the width for the linear layer in the
$\hat {\mathbf {z}}$
-component of the width for the linear layer in the
![]() $\hat {\mathbf {z}}$
-direction
$\hat {\mathbf {z}}$
-direction
![]() $W_z$
. Despite the limitations of the model (linear density profile, 2-D slab) and the difference in polarisation (X-mode versus O-mode), a qualitative comparison between figures 2(c) and 2(b) clearly shows that the analytic solution for the 2-D linear layer is able to recover the focusing behaviour observed in the numerical solution in toroidal geometry. This confirms that the beam focusing is not a numerical artefact. The beam focusing behaviour in the vicinity of the turning point is physical within the beam-tracing approximationFootnote
6
and motivates studying the beam-focusing phenomenon using the analytic solution to the beam-tracing equations in the 2-D linear-layer problem. In what follows, we describe the dependence of the analytic beam-tracing solution for
$W_z$
. Despite the limitations of the model (linear density profile, 2-D slab) and the difference in polarisation (X-mode versus O-mode), a qualitative comparison between figures 2(c) and 2(b) clearly shows that the analytic solution for the 2-D linear layer is able to recover the focusing behaviour observed in the numerical solution in toroidal geometry. This confirms that the beam focusing is not a numerical artefact. The beam focusing behaviour in the vicinity of the turning point is physical within the beam-tracing approximationFootnote
6
and motivates studying the beam-focusing phenomenon using the analytic solution to the beam-tracing equations in the 2-D linear-layer problem. In what follows, we describe the dependence of the analytic beam-tracing solution for
![]() $\Psi _{YY}$
on the initial conditions for the width
$\Psi _{YY}$
on the initial conditions for the width
![]() $W_0$
, the radius of curvature
$W_0$
, the radius of curvature
![]() $R_{Y0}$
and the vertical launch angle
$R_{Y0}$
and the vertical launch angle
![]() $\alpha _0$
. The initial condition is at
$\alpha _0$
. The initial condition is at
![]() $\tau =0$
, which corresponds to the plasma edge
$\tau =0$
, which corresponds to the plasma edge
![]() $x=0$
.
$x=0$
.

Figure 3. Thick coloured curves indicate values of the width
![]() $W_Y$
for varying initial incident angle
$W_Y$
for varying initial incident angle
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
$\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
![]() $80^{\circ }$
, and different initial
$80^{\circ }$
, and different initial
![]() $R_{Y0}$
(see legend) and fixed initial
$R_{Y0}$
(see legend) and fixed initial
![]() $W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. Corresponding dashed lines of same colour indicate vacuum values of
$W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. Corresponding dashed lines of same colour indicate vacuum values of
![]() $W_Y$
for same initial conditions as the thick coloured curves. The initial value of
$W_Y$
for same initial conditions as the thick coloured curves. The initial value of
![]() $R_{Y0}/L=-2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
(green) corresponds to the particular initial condition employed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). The vertical dotted points in grey indicate the location of the turning point, or cutoff (location where
$R_{Y0}/L=-2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
(green) corresponds to the particular initial condition employed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). The vertical dotted points in grey indicate the location of the turning point, or cutoff (location where
![]() $K_x=0$
).
$K_x=0$
).
We start by considering the analytic beam-tracing solution for
![]() $\Psi _{YY} = {K}/{R_Y} + i {2}/{W_Y^2}$
(Appendix A). In this beam-tracing solution, the dimensional quantities
$\Psi _{YY} = {K}/{R_Y} + i {2}/{W_Y^2}$
(Appendix A). In this beam-tracing solution, the dimensional quantities
![]() $K_0 = 2\pi /\lambda$
,
$K_0 = 2\pi /\lambda$
,
![]() $W_0$
and
$W_0$
and
![]() $L$
enter the equations through the beam parameter
$L$
enter the equations through the beam parameter
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
. Therefore, in the rest of the manuscript, only the beam parameter
$W_0/(\lambda L)^{\frac {1}{2}}$
. Therefore, in the rest of the manuscript, only the beam parameter
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
will be specified since it is the only parameter needed to determine the normalised solution
$W_0/(\lambda L)^{\frac {1}{2}}$
will be specified since it is the only parameter needed to determine the normalised solution
![]() $\Psi _{YY} ({L}/{K_0})$
. The beam width
$\Psi _{YY} ({L}/{K_0})$
. The beam width
![]() $W_Y$
is shown in figure 3 as a function of
$W_Y$
is shown in figure 3 as a function of
![]() $\tau$
for different initial conditions of the incident angle
$\tau$
for different initial conditions of the incident angle
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
$\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
![]() $80^{\circ }$
, and the initial radius of curvature
$80^{\circ }$
, and the initial radius of curvature
![]() $R_{Y0}$
(coloured curves). In this slab model, we assume that plasma is only present for
$R_{Y0}$
(coloured curves). In this slab model, we assume that plasma is only present for
![]() $x\gt 0$
and the vacuum exists for
$x\gt 0$
and the vacuum exists for
![]() $x\lt 0$
. Therefore, one needs to calculate the range of
$x\lt 0$
. Therefore, one needs to calculate the range of
![]() $\tau$
for which the central ray trajectory has positive
$\tau$
for which the central ray trajectory has positive
![]() $x_c$
. According to (2.9), for initial conditions at
$x_c$
. According to (2.9), for initial conditions at
![]() $\tau ^{\prime}=0$
, the plasma exit corresponds to
$\tau ^{\prime}=0$
, the plasma exit corresponds to
![]() $\tau ^{\prime} = 2\cos \alpha _0$
. The initial width
$\tau ^{\prime} = 2\cos \alpha _0$
. The initial width
![]() $W_0$
is kept fixed at
$W_0$
is kept fixed at
![]() $W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. The coloured dashed lines are the vacuum solutions (absence of plasma) with initial conditions corresponding to the respective
$W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. The coloured dashed lines are the vacuum solutions (absence of plasma) with initial conditions corresponding to the respective
![]() $W_Y$
of the same colour in the 2-D linear-layer problem. The vacuum solution initially follows the plasma solution until the beam approaches the turning point. The initial value of
$W_Y$
of the same colour in the 2-D linear-layer problem. The vacuum solution initially follows the plasma solution until the beam approaches the turning point. The initial value of
![]() $R_{Y0}/L=-2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
corresponds to the particular initial condition employed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) (see discussion in Appendix A). For that particular case, the initial radius of curvature takes the values
$R_{Y0}/L=-2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
corresponds to the particular initial condition employed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) (see discussion in Appendix A). For that particular case, the initial radius of curvature takes the values
![]() $R_{Y0}/L = -65.32, -6.93, -2.19$
and
$R_{Y0}/L = -65.32, -6.93, -2.19$
and
![]() $-0.3581$
respectively for
$-0.3581$
respectively for
![]() $\alpha _0=10^{\circ }, 30^{\circ }, 50^{\circ }$
and
$\alpha _0=10^{\circ }, 30^{\circ }, 50^{\circ }$
and
![]() $80^{\circ }$
. Here,
$80^{\circ }$
. Here,
![]() $R_{Y0}$
has little effect on the beam focusing around
$R_{Y0}$
has little effect on the beam focusing around
![]() $\tau ^{\prime} \approx 1$
for small angles, but has a non-negligible effect in the vicinity of the initial launch and after the turning point for the outgoing beam. These differences appear for small initial
$\tau ^{\prime} \approx 1$
for small angles, but has a non-negligible effect in the vicinity of the initial launch and after the turning point for the outgoing beam. These differences appear for small initial
![]() $|R_{Y0}|/L \lesssim 1$
, that is, for strongly focusing or diverging beams (see red and magenta curves in figure 3). The initial radius of curvature
$|R_{Y0}|/L \lesssim 1$
, that is, for strongly focusing or diverging beams (see red and magenta curves in figure 3). The initial radius of curvature
![]() $R_{Y0}$
becomes more important in the vicinity of the turning point for increasing incident angles, where the beam focusing location is shifted (see
$R_{Y0}$
becomes more important in the vicinity of the turning point for increasing incident angles, where the beam focusing location is shifted (see
![]() $\alpha _0 = 30^{\circ }$
). For
$\alpha _0 = 30^{\circ }$
). For
![]() $\alpha _0 = 50^{\circ }, 80^{\circ }$
, the beam focusing does not take place inside the plasma. The only focusing region corresponds to the beam waist that is captured by the vacuum solution. Note how the initial condition of
$\alpha _0 = 50^{\circ }, 80^{\circ }$
, the beam focusing does not take place inside the plasma. The only focusing region corresponds to the beam waist that is captured by the vacuum solution. Note how the initial condition of
![]() $R_{Y0}/L = -2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
from Gusakov, Irzak & Popov (Reference Gusakov, Irzak and Popov2014) and Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) strongly depends on the launch angle
$R_{Y0}/L = -2 {\cos \alpha _0}/{\sin ^2\alpha _0}$
from Gusakov, Irzak & Popov (Reference Gusakov, Irzak and Popov2014) and Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) strongly depends on the launch angle
![]() $\alpha _0$
: it defines a beam that is closer to a launch at the waist (
$\alpha _0$
: it defines a beam that is closer to a launch at the waist (
![]() $R_{Y0}/L = \infty$
) for small incident angles, but becomes strongly focusing (smaller, negative
$R_{Y0}/L = \infty$
) for small incident angles, but becomes strongly focusing (smaller, negative
![]() $R_{Y0}$
) for larger
$R_{Y0}$
) for larger
![]() $\alpha _0$
.
$\alpha _0$
.

Figure 4. Similar to figure 3 for varying initial width
![]() $W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40, 1.26$
and fixed
$W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40, 1.26$
and fixed
![]() $\alpha _0=30^{\circ }$
. For small
$\alpha _0=30^{\circ }$
. For small
![]() $W_0$
, the beam is initially strongly focused and experiences a large expansion (due to diffraction) that follows the vacuum solution before focusing slightly past the turning point (for all of
$W_0$
, the beam is initially strongly focused and experiences a large expansion (due to diffraction) that follows the vacuum solution before focusing slightly past the turning point (for all of
![]() $R_{Y0}$
). For increasing
$R_{Y0}$
). For increasing
![]() $W_0$
, the initial growth is less severe and the beam focusing depends on the initial
$W_0$
, the initial growth is less severe and the beam focusing depends on the initial
![]() $R_{Y0}$
. The beam even focuses twice along the path for particular initial conditions
$R_{Y0}$
. The beam even focuses twice along the path for particular initial conditions
![]() $R_{Y0}/L=-0.5, \alpha _0=30^{\circ }$
,
$R_{Y0}/L=-0.5, \alpha _0=30^{\circ }$
,
![]() $W_0 / (\lambda L)^{\frac {1}{2}} = 0.4$
(red in panel b), and
$W_0 / (\lambda L)^{\frac {1}{2}} = 0.4$
(red in panel b), and
![]() $1.26(\lambda L)^{\frac {1}{2}}$
(for the same
$1.26(\lambda L)^{\frac {1}{2}}$
(for the same
![]() $R_{Y0}/L, \alpha _0$
, red in panel c), where the first focusing region is the waist captured by the vacuum solution. Varying the initial width
$R_{Y0}/L, \alpha _0$
, red in panel c), where the first focusing region is the waist captured by the vacuum solution. Varying the initial width
![]() $W_0$
affects the initial expansion of the beam, from a pronounced initial expansion in panel (a,b) to no initial expansion for some
$W_0$
affects the initial expansion of the beam, from a pronounced initial expansion in panel (a,b) to no initial expansion for some
![]() $R_{Y0}/L$
in panel (c). The inset in panel (c) focuses on the initial propagation region, which exhibits converging or diverging beams depending on the initial conditions.
$R_{Y0}/L$
in panel (c). The inset in panel (c) focuses on the initial propagation region, which exhibits converging or diverging beams depending on the initial conditions.
Figure 4 shows the beam width for different initial conditions
![]() $W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.4, 1.26$
, and the same scan in
$W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.4, 1.26$
, and the same scan in
![]() $R_{Y0}/L$
as in figure 3, all while keeping a fixed initial incident angle
$R_{Y0}/L$
as in figure 3, all while keeping a fixed initial incident angle
![]() $\alpha _0=30^{\circ }$
. For small
$\alpha _0=30^{\circ }$
. For small
![]() $W_0=0.13(\lambda L)^{\frac {1}{2}}$
, the beam width
$W_0=0.13(\lambda L)^{\frac {1}{2}}$
, the beam width
![]() $W_Y$
initially follows closely the vacuum solution (dashed line), independent of the initial conditions
$W_Y$
initially follows closely the vacuum solution (dashed line), independent of the initial conditions
![]() $W_0$
and
$W_0$
and
![]() $R_{Y0}$
. Small
$R_{Y0}$
. Small
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
corresponds to a highly focused beam. Diffraction produces a strong initial expansion of the beam width
$W_0/(\lambda L)^{\frac {1}{2}}$
corresponds to a highly focused beam. Diffraction produces a strong initial expansion of the beam width
![]() $W_Y$
, which is followed by strong focusing slightly past the turning point (for all of
$W_Y$
, which is followed by strong focusing slightly past the turning point (for all of
![]() $R_{Y0}$
). For
$R_{Y0}$
). For
![]() $W_0=0.40(\lambda L)^{\frac {1}{2}}$
, the initial growth is less severe and the beam focusing (value and location) exhibits a noticeable dependence on the initial
$W_0=0.40(\lambda L)^{\frac {1}{2}}$
, the initial growth is less severe and the beam focusing (value and location) exhibits a noticeable dependence on the initial
![]() $R_{Y0}$
. The dependence on the initial
$R_{Y0}$
. The dependence on the initial
![]() $R_{Y0}$
is even more noticeable for
$R_{Y0}$
is even more noticeable for
![]() $W_0=1.26(\lambda L)^{\frac {1}{2}}$
, especially for the focus location: the beam even focuses twice along the beam for
$W_0=1.26(\lambda L)^{\frac {1}{2}}$
, especially for the focus location: the beam even focuses twice along the beam for
![]() $R_{Y0}/L=-0.5$
(red curve), which is an initially focusing beam at the plasma edge (the first focusing region is the waist captured by the vacuum solution). The double focusing happens for both
$R_{Y0}/L=-0.5$
(red curve), which is an initially focusing beam at the plasma edge (the first focusing region is the waist captured by the vacuum solution). The double focusing happens for both
![]() $W_0 = 0.4 (\lambda L)^{\frac {1}{2}}$
and
$W_0 = 0.4 (\lambda L)^{\frac {1}{2}}$
and
![]() $W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
. Comparing the same initial condition
$W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
. Comparing the same initial condition
![]() $R_{Y0}=\infty$
(launch at waist, black curve) between the different initial
$R_{Y0}=\infty$
(launch at waist, black curve) between the different initial
![]() $W_0$
, we see that the beam focusing location takes place after the turning point for small initial
$W_0$
, we see that the beam focusing location takes place after the turning point for small initial
![]() $W_0 = 0.13, 0.40 (\lambda L)^{\frac {1}{2}}$
and approaches the turning point for large
$W_0 = 0.13, 0.40 (\lambda L)^{\frac {1}{2}}$
and approaches the turning point for large
![]() $W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
(the turning point location is given by the vertical dotted lines). This discussion has important consequences for interpreting the regions in the plasma with predominant contributions to backscattering in DBS measurements, as will be discussed in § 4.
$W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
(the turning point location is given by the vertical dotted lines). This discussion has important consequences for interpreting the regions in the plasma with predominant contributions to backscattering in DBS measurements, as will be discussed in § 4.
In this section, we have seen how the 2-D linear-layer model exhibits focusing of the beam width around the cutoff. This focusing is separate from the focusing caused at the beam waist in vacuum. The beam focusing depends on the initial conditions for the incident angle
![]() $\alpha _0$
, normalised beam parameter
$\alpha _0$
, normalised beam parameter
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
and radius of curvature
$W_0/(\lambda L)^{\frac {1}{2}}$
and radius of curvature
![]() $R_{Y0}/L$
. Beam focusing tends to be enhanced for small
$R_{Y0}/L$
. Beam focusing tends to be enhanced for small
![]() $\alpha _0$
, while it tends to disappear for large
$\alpha _0$
, while it tends to disappear for large
![]() $\alpha _0$
. For small
$\alpha _0$
. For small
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
, strong initial growth precedes strong focusing. For large
$W_0/(\lambda L)^{\frac {1}{2}}$
, strong initial growth precedes strong focusing. For large
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
, the beam focuses from the initial condition towards the focusing region, and the initial growth disappears for some initial conditions. These phenomena are not captured by the vacuum solution.
$W_0/(\lambda L)^{\frac {1}{2}}$
, the beam focuses from the initial condition towards the focusing region, and the initial growth disappears for some initial conditions. These phenomena are not captured by the vacuum solution.
Having gained an understanding of the phenomenon of beam focusing, in what follows, we will use the analytical 2-D model solution to assess the impact of beam focusing on Doppler backscattering measurements.
3. Beam-tracing model for DBS in the 2-D linear layer
In the previous section, we have shown the behaviour of the width
![]() $W_Y$
of a microwave beam propagating in a 2-D linear layer. In this section, we will use that solution to find the backscattered signal amplitude and power in DBS measurements. This will allow us to study how the phenomenon of beam focusing impacts the scattered power measured by DBS. We will see how the scattered power can be written as the integral over
$W_Y$
of a microwave beam propagating in a 2-D linear layer. In this section, we will use that solution to find the backscattered signal amplitude and power in DBS measurements. This will allow us to study how the phenomenon of beam focusing impacts the scattered power measured by DBS. We will see how the scattered power can be written as the integral over
![]() $k$
-space of a filter function
$k$
-space of a filter function
![]() $|F_{xy}|^2$
multiplied by the Fourier transform of the turbulence correlation function, which corresponds to the density-fluctuation power spectrum. We will also see how the dependence of the filter function on
$|F_{xy}|^2$
multiplied by the Fourier transform of the turbulence correlation function, which corresponds to the density-fluctuation power spectrum. We will also see how the dependence of the filter function on
![]() $k_x$
and
$k_x$
and
![]() $k_y$
is not trivial, and we will show how
$k_y$
is not trivial, and we will show how
![]() $|F_{xy}|^2$
can be enhanced in the vicinity of the focusing region, where
$|F_{xy}|^2$
can be enhanced in the vicinity of the focusing region, where
![]() $W_Y$
reaches a minimum. The formulae that we obtain using a beam-tracing model for DBS recover previous analytic work based on a 2-D Cartesian slab by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) and connect it with more recent work based on a beam-tracing model of DBS in full toroidal geometry (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). To do so, we use a representation of the density fluctuations in 2-D Cartesian coordinates, as done by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). A representation aligned along the beam trajectory, or beam-aligned representation (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), is not used in the main body of this manuscript. In Appendices C and D, we use the beam-aligned representation of the density to show the equivalence between the beam model by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). For the purposes of calculating the scattered power contributions along the beam path, we show in Appendices C and D that both representations of the density are related to each other by a rotation. With respect to the wavenumber resolution, the situation is more subtle and one cannot simply assume that both representations of the density are related by a rotation. This will be the subject of an upcoming publication.
$W_Y$
reaches a minimum. The formulae that we obtain using a beam-tracing model for DBS recover previous analytic work based on a 2-D Cartesian slab by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) and connect it with more recent work based on a beam-tracing model of DBS in full toroidal geometry (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). To do so, we use a representation of the density fluctuations in 2-D Cartesian coordinates, as done by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). A representation aligned along the beam trajectory, or beam-aligned representation (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), is not used in the main body of this manuscript. In Appendices C and D, we use the beam-aligned representation of the density to show the equivalence between the beam model by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). For the purposes of calculating the scattered power contributions along the beam path, we show in Appendices C and D that both representations of the density are related to each other by a rotation. With respect to the wavenumber resolution, the situation is more subtle and one cannot simply assume that both representations of the density are related by a rotation. This will be the subject of an upcoming publication.
We start by defining the Cartesian representation of the density fluctuations, or lab-frame density-fluctuation amplitude. We expand the density fluctuations in
![]() $\mathbf {r} = (x,y,z)$
as follows
$\mathbf {r} = (x,y,z)$
as follows
where
![]() $x$
and
$x$
and
![]() $y$
are the directions perpendicular to the magnetic field, and
$y$
are the directions perpendicular to the magnetic field, and
![]() $z$
is along the magnetic field (see figure 1 for the 2-D linear layer). In the 2-D linear layer, the density fluctuations in (3.1) are evaluated at
$z$
is along the magnetic field (see figure 1 for the 2-D linear layer). In the 2-D linear layer, the density fluctuations in (3.1) are evaluated at
![]() $z=0$
. A point
$z=0$
. A point
![]() $(x,y)$
in the 2-D plane is given by
$(x,y)$
in the 2-D plane is given by
where
![]() $\big ( x_c(\tau ), y_c(\tau ) \big )$
in (3.2) are the coordinates along the central ray (figure 1 and Appendix A), and
$\big ( x_c(\tau ), y_c(\tau ) \big )$
in (3.2) are the coordinates along the central ray (figure 1 and Appendix A), and
![]() $\alpha$
is the angle between the central ray tangent vector
$\alpha$
is the angle between the central ray tangent vector
![]() ${\hat{\mathbf{g}}}$
and the horizontal (
${\hat{\mathbf{g}}}$
and the horizontal (
![]() $\sin \alpha$
and
$\sin \alpha$
and
![]() $\cos \alpha$
are given by (A.9)). The wavevector of the turbulence is written in its Cartesian components
$\cos \alpha$
are given by (A.9)). The wavevector of the turbulence is written in its Cartesian components
![]() $\mathbf {k}_\perp = k_x {\hat{\mathbf{x}}} + k_y {\hat{\mathbf{y}}}$
(figure 1). Here, the Cartesian
$\mathbf {k}_\perp = k_x {\hat{\mathbf{x}}} + k_y {\hat{\mathbf{y}}}$
(figure 1). Here, the Cartesian
![]() $k_x$
naturally corresponds to the radial direction, or normal to the flux surface, and
$k_x$
naturally corresponds to the radial direction, or normal to the flux surface, and
![]() $k_y$
corresponds to the binormal component, that is, the component in the flux surface and perpendicular to the magnetic field. This is a useful frame in which to express turbulent fluctuations perpendicular to the background magnetic field (Catto Reference Catto1978; Frieman & Chen Reference Frieman and Chen1982).
$k_y$
corresponds to the binormal component, that is, the component in the flux surface and perpendicular to the magnetic field. This is a useful frame in which to express turbulent fluctuations perpendicular to the background magnetic field (Catto Reference Catto1978; Frieman & Chen Reference Frieman and Chen1982).
Having introduced the representation of the density fluctuations, we calculate the backscattered amplitude and power. To do so, we use a theoretical beam-tracing model of DBS (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ) that gives an analytical relationship between the beam electric field and the scattered amplitude. As shown in Appendix B, the scattered amplitude takes an analogous form to (153) from Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ),
where
![]() $({x}_{c\mu }, {y}_{c\mu }) = \big ( x_c({\tau }_\mu ), y_c({\tau }_\mu ) \big )$
denote the point along the central ray trajectory evaluated at a particular
$({x}_{c\mu }, {y}_{c\mu }) = \big ( x_c({\tau }_\mu ), y_c({\tau }_\mu ) \big )$
denote the point along the central ray trajectory evaluated at a particular
![]() $\tau = {\tau }_\mu$
, and
$\tau = {\tau }_\mu$
, and
![]() $x_c$
and
$x_c$
and
![]() $y_c$
are given by (2.9). The subscript
$y_c$
are given by (2.9). The subscript
![]() $(.)_\mu$
means that functions are evaluated at a point along the trajectory
$(.)_\mu$
means that functions are evaluated at a point along the trajectory
![]() $\tau = {\tau }_\mu$
that satisfies the Bragg condition for backscattering (3.4). In (3.3), the phase in the argument of the exponent is equivalent to the phase
$\tau = {\tau }_\mu$
that satisfies the Bragg condition for backscattering (3.4). In (3.3), the phase in the argument of the exponent is equivalent to the phase
![]() $2s_\mu + k_1 l_\mu$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) (where
$2s_\mu + k_1 l_\mu$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) (where
![]() $k_1$
is written as
$k_1$
is written as
![]() $k_{\perp ,1}$
), and it is ordered large
$k_{\perp ,1}$
), and it is ordered large
![]() $\sim L/\lambda$
. The filter function
$\sim L/\lambda$
. The filter function
![]() $F_{xy,\mu }(k_x, k_y)$
is the Cartesian equivalent to
$F_{xy,\mu }(k_x, k_y)$
is the Cartesian equivalent to
![]() $F_\mu (k_1,k_2)$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). The expression for
$F_\mu (k_1,k_2)$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). The expression for
![]() $F_{xy,\mu }$
is given in Appendix B. For the rest of the manuscript, we will only need the magnitude of
$F_{xy,\mu }$
is given in Appendix B. For the rest of the manuscript, we will only need the magnitude of
![]() $F_{xy,\mu }$
, given in (3.8). Note that the expression for
$F_{xy,\mu }$
, given in (3.8). Note that the expression for
![]() $A_r(t)$
is related to the spectral amplitude
$A_r(t)$
is related to the spectral amplitude
![]() $\tilde {A}_r(\omega )$
by the Fourier transform
$\tilde {A}_r(\omega )$
by the Fourier transform
![]() $\mathscr {F}$
in time,
$\mathscr {F}$
in time,
![]() $\tilde {A}_r(\omega ) = \mathscr {F} \big [A_r(t)\big ] (\omega ) = (2\pi )^{-1} \int {A_r(t) \exp (i\omega t) \text {d}t}$
(only
$\tilde {A}_r(\omega ) = \mathscr {F} \big [A_r(t)\big ] (\omega ) = (2\pi )^{-1} \int {A_r(t) \exp (i\omega t) \text {d}t}$
(only
![]() $\delta n$
is assumed to depend on time). In this manuscript, we will preferentially work with
$\delta n$
is assumed to depend on time). In this manuscript, we will preferentially work with
![]() $A_r(t)$
.
$A_r(t)$
.
As we announced above, the location
![]() ${\tau }_\mu$
is defined by the condition of stationary phase (Bender & Orszag Reference Bender and Orszag1978), given to lowest order by
${\tau }_\mu$
is defined by the condition of stationary phase (Bender & Orszag Reference Bender and Orszag1978), given to lowest order by
Equation (3.4) can be rewritten as
![]() $2K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu = 0$
, where
$2K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu = 0$
, where
![]() $\hat {\mathbf {g}} = \cos \alpha \ \hat {\mathbf {x}} + \sin \alpha \ \hat {\mathbf {y}}$
from (2.6). The components
$\hat {\mathbf {g}} = \cos \alpha \ \hat {\mathbf {x}} + \sin \alpha \ \hat {\mathbf {y}}$
from (2.6). The components
![]() $\cos \alpha$
and
$\cos \alpha$
and
![]() $\sin \alpha$
can be calculated explicitly using the ray trajectory from (2.9), and the fact that
$\sin \alpha$
can be calculated explicitly using the ray trajectory from (2.9), and the fact that
![]() $\cos \alpha = {\text {d}x_c}/{\text {d}l}, \ \sin \alpha = {\text {d}y_c}/{\text {d}l}$
and the element of path length is
$\cos \alpha = {\text {d}x_c}/{\text {d}l}, \ \sin \alpha = {\text {d}y_c}/{\text {d}l}$
and the element of path length is
![]() $\text {d} l = g \text {d}\tau$
, which recovers (A.9). It will be useful to introduce the projections of the turbulence wavevector
$\text {d} l = g \text {d}\tau$
, which recovers (A.9). It will be useful to introduce the projections of the turbulence wavevector
![]() $\mathbf {k}_\perp$
along
$\mathbf {k}_\perp$
along
![]() $\hat {\mathbf {g}}$
and
$\hat {\mathbf {g}}$
and
![]() $\hat {\mathbf {Y}}$
,
$\hat {\mathbf {Y}}$
,
which defines a rotation in the 2-D
![]() $(x,y)$
plane for every point along the beam path denoted by
$(x,y)$
plane for every point along the beam path denoted by
![]() $\tau$
(note that
$\tau$
(note that
![]() $\alpha$
depends on
$\alpha$
depends on
![]() $\tau$
through the trajectory in (2.9)).
$\tau$
through the trajectory in (2.9)).
To solve (3.4), we notice that
![]() $k_y + 2K_0\sin \alpha _0 \sim 1/W \ll 1/\lambda$
(see Appendix B). The equation for
$k_y + 2K_0\sin \alpha _0 \sim 1/W \ll 1/\lambda$
(see Appendix B). The equation for
![]() ${\tau }_\mu$
is then
${\tau }_\mu$
is then
Note that (3.6) defines a
![]() ${\tau }_\mu$
that fails near the turning point
${\tau }_\mu$
that fails near the turning point
![]() $k_x \approx 0$
, but this divergence will not cause problems. More details are given in Appendix B.
$k_x \approx 0$
, but this divergence will not cause problems. More details are given in Appendix B.
From (3.3), we calculate the scattered power, which takes an analogous form to (177) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ),
where the slowly varying filter
![]() $|F_{xy,\mu }|^2(k_x, k_y)$
is
$|F_{xy,\mu }|^2(k_x, k_y)$
is
 \begin{align} \begin{alignedat}{3} & |F_{xy,\mu }|^2(k_x, k_y) &&= 2 \pi \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \frac { \Im [{{\Psi }}_{YY}]_\mu }{| {\Psi }_{YY}|_\mu } \frac { \exp \Bigg [ - \frac { \big (2 \frac {\text {d} {K} }{\text {d}\tau } \big )_\mu ^2 {g}_\mu ^2 }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY}} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu ^2 } \frac {2 \left ( \mathbf {k}_{\perp } \cdot \hat {\mathbf {Y}}_\mu \right )^2 }{\Delta {k}_{\mu 2}^2} \Bigg ] }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY} } \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu } . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{3} & |F_{xy,\mu }|^2(k_x, k_y) &&= 2 \pi \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \frac { \Im [{{\Psi }}_{YY}]_\mu }{| {\Psi }_{YY}|_\mu } \frac { \exp \Bigg [ - \frac { \big (2 \frac {\text {d} {K} }{\text {d}\tau } \big )_\mu ^2 {g}_\mu ^2 }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY}} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu ^2 } \frac {2 \left ( \mathbf {k}_{\perp } \cdot \hat {\mathbf {Y}}_\mu \right )^2 }{\Delta {k}_{\mu 2}^2} \Bigg ] }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY} } \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu } . \end{alignedat} \end{align}
Here,
![]() $m_e$
is the electron mass,
$m_e$
is the electron mass,
![]() $e$
the electron charge,
$e$
the electron charge,
![]() $\epsilon _0$
is the vacuum permittivity and
$\epsilon _0$
is the vacuum permittivity and
![]() $\langle . \rangle _T$
is an ensemble average, which we compute as a time average over a period of length
$\langle . \rangle _T$
is an ensemble average, which we compute as a time average over a period of length
![]() $T$
. The Gaussian exponential term in
$T$
. The Gaussian exponential term in
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}$
in (3.7), entering through
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}$
in (3.7), entering through
![]() $|F_{xy,\mu }|^2$
in (3.8), is to be considered as a Gaussian exponential in
$|F_{xy,\mu }|^2$
in (3.8), is to be considered as a Gaussian exponential in
![]() $k_y$
, where
$k_y$
, where
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}$
is defined in terms of
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}$
is defined in terms of
![]() $k_x$
and
$k_x$
and
![]() $k_y$
by (3.5). Note that all functions of
$k_y$
by (3.5). Note that all functions of
![]() $\tau$
in (3.8) are evaluated at
$\tau$
in (3.8) are evaluated at
![]() $\tau = {\tau }_\mu$
. Here,
$\tau = {\tau }_\mu$
. Here,
![]() ${\alpha }_\mu = \alpha ({\tau }_\mu )$
is the vertical incidence angle at
${\alpha }_\mu = \alpha ({\tau }_\mu )$
is the vertical incidence angle at
![]() $\tau = {\tau }_\mu$
, figure 1. The functions of
$\tau = {\tau }_\mu$
, figure 1. The functions of
![]() $\tau _\mu$
in
$\tau _\mu$
in
![]() $|F_{xy,\mu }(k_x, k_y)|^2$
in (3.8) are functions of
$|F_{xy,\mu }(k_x, k_y)|^2$
in (3.8) are functions of
![]() $(k_x, k_y)$
through the Bragg condition relating
$(k_x, k_y)$
through the Bragg condition relating
![]() ${\tau }_{\mu }$
to
${\tau }_{\mu }$
to
![]() $k_x$
and
$k_x$
and
![]() $k_y$
((3.4), (3.6)).
$k_y$
((3.4), (3.6)).
In (3.8), we have introduced the wavenumber resolution, given by
![]() $\Delta k_{\mu 2}^2 = { 4 | {\Psi }_{YY\mu }|^2 }/{ \Im [ {\Psi }_{YY\mu }] }$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). In the context of the 2-D linear layer, the quantity
$\Delta k_{\mu 2}^2 = { 4 | {\Psi }_{YY\mu }|^2 }/{ \Im [ {\Psi }_{YY\mu }] }$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). In the context of the 2-D linear layer, the quantity
![]() $\Delta {k}_{\mu 2}$
is a measure of the resolution in the wavenumber component that is perpendicular to
$\Delta {k}_{\mu 2}$
is a measure of the resolution in the wavenumber component that is perpendicular to
![]() $\hat {\mathbf {g}}$
. This is because
$\hat {\mathbf {g}}$
. This is because
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
is the component of
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
is the component of
![]() $\mathbf {k}_\perp$
in the perpendicular direction to
$\mathbf {k}_\perp$
in the perpendicular direction to
![]() $\hat {\mathbf {g}}$
(see (3.5)). The dependence of (3.8) on
$\hat {\mathbf {g}}$
(see (3.5)). The dependence of (3.8) on
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
therefore implies
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
therefore implies
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \sim 1/W$
, that is,
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \sim 1/W$
, that is,
![]() $ k_x \approx k_y \cos {\alpha }_\mu /\sin {\alpha }_\mu$
, because
$ k_x \approx k_y \cos {\alpha }_\mu /\sin {\alpha }_\mu$
, because
![]() $\Delta {k}_{\mu 2} \sim 1/W \ll 1/\lambda$
. The resolution
$\Delta {k}_{\mu 2} \sim 1/W \ll 1/\lambda$
. The resolution
![]() $\Delta k_{\mu 2}$
is of limited interest in this manuscript, beyond the fact that it is of order
$\Delta k_{\mu 2}$
is of limited interest in this manuscript, beyond the fact that it is of order
![]() $\sim 1/W$
.
$\sim 1/W$
.
The Gaussian exponential term in
![]() $k_y$
from (3.8) allows us to calculate the wavenumber resolution in the lab frame, or DBS
$k_y$
from (3.8) allows us to calculate the wavenumber resolution in the lab frame, or DBS
![]() $k_y$
-resolution
$k_y$
-resolution
![]() $\Delta k_y$
(see Appendix B). The final expression for the scattered power, expressed in terms of
$\Delta k_y$
(see Appendix B). The final expression for the scattered power, expressed in terms of
![]() $k_x$
and
$k_x$
and
![]() $k_y$
, is
$k_y$
, is
 \begin{align} \begin{alignedat}{2} &\frac {p_r}{P_{ant}} && \approx 2^{\frac {1}{2}} \pi \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \frac {K_0^2L}{\Delta k_y} \int {\text {d}k_x \text {d}k_y } \frac { \exp \big [{-}{2\big(k_y + 2K_{0}\sin \alpha _0 \big)^2/\Delta k_y^2} \big ] }{ K_\mu W_{Y\mu } } \big\langle |\delta \hat {n} (k_x, k_y)|^2 \big\rangle _T \\ & && \approx \pi ^{\frac {3}{2}} K_0^2L \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \int {\text {d}k_x } \frac {\big \langle |\delta \hat {n} (k_x, - 2 K_{0}\sin \alpha _0)|^2 \big\rangle _T }{ K_\mu W_{Y\mu } }, \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} &\frac {p_r}{P_{ant}} && \approx 2^{\frac {1}{2}} \pi \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \frac {K_0^2L}{\Delta k_y} \int {\text {d}k_x \text {d}k_y } \frac { \exp \big [{-}{2\big(k_y + 2K_{0}\sin \alpha _0 \big)^2/\Delta k_y^2} \big ] }{ K_\mu W_{Y\mu } } \big\langle |\delta \hat {n} (k_x, k_y)|^2 \big\rangle _T \\ & && \approx \pi ^{\frac {3}{2}} K_0^2L \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \int {\text {d}k_x } \frac {\big \langle |\delta \hat {n} (k_x, - 2 K_{0}\sin \alpha _0)|^2 \big\rangle _T }{ K_\mu W_{Y\mu } }, \\ \end{alignedat} \end{align}
where we have defined the
![]() $k_y$
resolution of the DBS diagnostic as
$k_y$
resolution of the DBS diagnostic as
Equation (3.9) defines a one-dimensional filter
![]() $|F_{x\mu }|^2$
, given by
$|F_{x\mu }|^2$
, given by
where the product
![]() $K_\mu W_{Y\mu }$
is given by
$K_\mu W_{Y\mu }$
is given by
 \begin{align} {K_\mu } W_{Y\mu } &= \frac {K_0}{\left ( 2\Im [\Psi _{yy0}] \right )^{\frac {1}{2}} } \bigg | - \frac {k_{x}}{K_0} \nonumber \\& \quad+ \Psi _{yy0}^{\prime} \bigg ({-} 2\frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac {k_{x}}{K_0} + 4\sin ^2\alpha _0 - \frac {k_{x}^2}{K_0^2} \bigg ) \bigg | . \end{align}
\begin{align} {K_\mu } W_{Y\mu } &= \frac {K_0}{\left ( 2\Im [\Psi _{yy0}] \right )^{\frac {1}{2}} } \bigg | - \frac {k_{x}}{K_0} \nonumber \\& \quad+ \Psi _{yy0}^{\prime} \bigg ({-} 2\frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac {k_{x}}{K_0} + 4\sin ^2\alpha _0 - \frac {k_{x}^2}{K_0^2} \bigg ) \bigg | . \end{align}
In (3.12), we used the beam-tracing analytic solution for
![]() $W_Y = W_{Y}(\tau )$
((2.10), Appendix A) as well as the expression for
$W_Y = W_{Y}(\tau )$
((2.10), Appendix A) as well as the expression for
![]() $K = K(\tau )$
in the 2-D linear-layer problem.
$K = K(\tau )$
in the 2-D linear-layer problem.
The first approximately equal sign in (3.9) recovers the expected Gaussian exponential dependence of the power with
![]() $k_y$
. Note how the exponential term in (3.8) has explicit dependence on
$k_y$
. Note how the exponential term in (3.8) has explicit dependence on
![]() $k_x$
and
$k_x$
and
![]() $k_y$
through
$k_y$
through
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
. In addition, there is an additional dependence on
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu$
. In addition, there is an additional dependence on
![]() $k_x$
and
$k_x$
and
![]() $k_y$
that appears through
$k_y$
that appears through
![]() $\tau _\mu$
, given by (3.6). Equation (3.9) is the lowest-order contribution to the Gaussian exponential term in (3.8), and shows that the selected wavenumber
$\tau _\mu$
, given by (3.6). Equation (3.9) is the lowest-order contribution to the Gaussian exponential term in (3.8), and shows that the selected wavenumber
![]() $k_y$
is given approximately by
$k_y$
is given approximately by
![]() $k_y \approx -2K_0\sin \alpha _0 \sim 1/\lambda$
, and the correction to that is ordered
$k_y \approx -2K_0\sin \alpha _0 \sim 1/\lambda$
, and the correction to that is ordered
![]() $\sim 1/W$
. This justifies the first approximately equal sign in (3.9). The second approximately equal sign in (3.9) can be justified by the separation of scales in the integral in
$\sim 1/W$
. This justifies the first approximately equal sign in (3.9). The second approximately equal sign in (3.9) can be justified by the separation of scales in the integral in
![]() $k_y$
: on the one hand, the spectrum
$k_y$
: on the one hand, the spectrum
![]() $\langle |\delta \hat {n}(k_x, k_y) |^2 \rangle _T$
depends on
$\langle |\delta \hat {n}(k_x, k_y) |^2 \rangle _T$
depends on
![]() $k_y \sim 1/\lambda$
; on the other hand, the resolution in (3.10) scales as
$k_y \sim 1/\lambda$
; on the other hand, the resolution in (3.10) scales as
![]() $\Delta k_y \sim 1/W$
, which means that the exponential term in (3.9) scales as
$\Delta k_y \sim 1/W$
, which means that the exponential term in (3.9) scales as
![]() $\sim \exp [{-} W^2/\lambda ^2]$
if one assumes that
$\sim \exp [{-} W^2/\lambda ^2]$
if one assumes that
![]() $k_y + 2 K_0 \sin \alpha _0 \sim 1/\lambda$
. The integral in
$k_y + 2 K_0 \sin \alpha _0 \sim 1/\lambda$
. The integral in
![]() $k_y$
can therefore be calculated via Laplace’s method, which results in the second approximately equal sign in (3.9). More details can be found in Appendix B.
$k_y$
can therefore be calculated via Laplace’s method, which results in the second approximately equal sign in (3.9). More details can be found in Appendix B.
Importantly, (3.9), (3.10) and (3.12) recover (16) of Gusakov et al. (Reference Gusakov, Irzak and Popov2014), which was extended to (14) and (15) of Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) for the cross-correlation function CCF. Gusakov et al. carry their analysis for radial correlation Doppler reflectometry (RCDR), and not for standard DBS, as done in this manuscript. In RCDR, one is interested in the cross-correlation function CCF
![]() $(\Delta x)$
, which depends on the radial separation
$(\Delta x)$
, which depends on the radial separation
![]() $\Delta x$
between DBS scattering locations. The scattered power calculated in this work can be recovered by setting
$\Delta x$
between DBS scattering locations. The scattered power calculated in this work can be recovered by setting
![]() $\Delta x = 0$
in the work by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) (power is auto correlation). Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) also use a particular initial condition
$\Delta x = 0$
in the work by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) (power is auto correlation). Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) also use a particular initial condition
![]() $\Psi _{yy0}^{\prime} = i {K_0L}/{(K_0 \rho )^2}$
, where
$\Psi _{yy0}^{\prime} = i {K_0L}/{(K_0 \rho )^2}$
, where
![]() $\rho$
is related to the launched beam width. One can see that setting the particular initial condition for
$\rho$
is related to the launched beam width. One can see that setting the particular initial condition for
![]() $\Psi _{yy0}^{\prime} = i {K_0L}/{(K_0 \rho )^2}$
in (3.12) recovers (14) and (15) of Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) for
$\Psi _{yy0}^{\prime} = i {K_0L}/{(K_0 \rho )^2}$
in (3.12) recovers (14) and (15) of Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) for
![]() $\Delta x = 0$
.
$\Delta x = 0$
.
The backscattered power can be written as an integral along the path
![]() $l$
((196) of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). This can be achieved by realising that the Bragg condition and the fact that
$l$
((196) of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). This can be achieved by realising that the Bragg condition and the fact that
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \approx 0$
imply
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \approx 0$
imply
![]() $k_x \approx - 2 {K}_{x\mu }$
(3.5). Having integrated in
$k_x \approx - 2 {K}_{x\mu }$
(3.5). Having integrated in
![]() $k_y$
, the scattered
$k_y$
, the scattered
![]() $k_x$
along the Cartesian
$k_x$
along the Cartesian
![]() $x$
-direction can parametrise the location along the path. To express the
$x$
-direction can parametrise the location along the path. To express the
![]() $k_x$
-integral (3.9) in terms of
$k_x$
-integral (3.9) in terms of
![]() $l$
, change the integration variable using
$l$
, change the integration variable using
![]() $\text {d}k_x = 2 K_\mu |\text {d}K_\mu /\text {d}\tau | \text {d}l / |g_\mu K_{x\mu }| = 2 \text {d}l / (gL)$
, where we used (B.25). Then, the denominator under the integral sign
$\text {d}k_x = 2 K_\mu |\text {d}K_\mu /\text {d}\tau | \text {d}l / |g_\mu K_{x\mu }| = 2 \text {d}l / (gL)$
, where we used (B.25). Then, the denominator under the integral sign
![]() $\int \text {d}k_x$
can be explicitly expressed as a function of the path length
$\int \text {d}k_x$
can be explicitly expressed as a function of the path length
![]() $l$
. Additional details on the calculation are given in Appendices A and B. We find
$l$
. Additional details on the calculation are given in Appendices A and B. We find
Equation (3.13) closely connects to the expression for the scattered power in (196) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). In that case,
![]() $1/g^2$
is the ray piece, while the beam piece can still be written as
$1/g^2$
is the ray piece, while the beam piece can still be written as
![]() ${1}/{W_{Y}}$
. We see that
${1}/{W_{Y}}$
. We see that
![]() $W_Y$
plays an explicit role in the
$W_Y$
plays an explicit role in the
![]() $k_x$
wavenumber resolution (see (3.9)) and equivalently in the spatial localisation of the power along the beam path (see (3.13)). Finally, (3.13) may seem to contradict our prediction that the scattered power scales as
$k_x$
wavenumber resolution (see (3.9)) and equivalently in the spatial localisation of the power along the beam path (see (3.13)). Finally, (3.13) may seem to contradict our prediction that the scattered power scales as
![]() $\sim 1/g$
. Note that in (3.13), one of the factors of
$\sim 1/g$
. Note that in (3.13), one of the factors of
![]() $g$
comes from the change of integration variable from
$g$
comes from the change of integration variable from
![]() $k_x$
to
$k_x$
to
![]() $l$
.
$l$
.
Next, we discuss the filter function
![]() $|F_{x\mu }|^2 \propto 1/K_\mu W_{Y\mu }$
in (3.11). Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) argue that non-local forward-scattering events produced by large-radial-scale fluctuations cause the denominator of
$|F_{x\mu }|^2 \propto 1/K_\mu W_{Y\mu }$
in (3.11). Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) argue that non-local forward-scattering events produced by large-radial-scale fluctuations cause the denominator of
![]() $|F_{xy,\mu }|^2$
to approach zero. This happens for specific
$|F_{xy,\mu }|^2$
to approach zero. This happens for specific
![]() $k_x$
and should cause an enhancement in the DBS signal. Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) state that this enhancement is due to forward-scattering events taking place all along the beam path through the plasma, making the DBS measurement spatially non-local. They argue that this effect should preferentially enhance the DBS signal for small incidence angles
$k_x$
and should cause an enhancement in the DBS signal. Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) state that this enhancement is due to forward-scattering events taking place all along the beam path through the plasma, making the DBS measurement spatially non-local. They argue that this effect should preferentially enhance the DBS signal for small incidence angles
![]() $\alpha _0$
, which they observe as an enhancement in the CCF. In our work, forward scattering is absent by design. Our model only includes contributions from backscattering events, which are selected through the Bragg condition in (3.4) and (3.6). Equation (3.9) shows that all the contributions to the so-called forward scattering can be explained by the filter function, which is the term
$\alpha _0$
, which they observe as an enhancement in the CCF. In our work, forward scattering is absent by design. Our model only includes contributions from backscattering events, which are selected through the Bragg condition in (3.4) and (3.6). Equation (3.9) shows that all the contributions to the so-called forward scattering can be explained by the filter function, which is the term
![]() $ \propto 1/KW_Y$
in (3.9), or equivalently
$ \propto 1/KW_Y$
in (3.9), or equivalently
![]() $\propto 1/g^2 W_Y$
when written as an integral in
$\propto 1/g^2 W_Y$
when written as an integral in
![]() $l$
. Importantly, in § 4, we will see how the focusing effect due to
$l$
. Importantly, in § 4, we will see how the focusing effect due to
![]() $W_Y$
can be far greater than the decrease of
$W_Y$
can be far greater than the decrease of
![]() $K$
near the turning point. It is therefore crucial to understand the behaviour of
$K$
near the turning point. It is therefore crucial to understand the behaviour of
![]() $W_Y$
to understand its effect on the backscattered signal. In this work, we interpret (3.9) and the signal enhancement produced for specific
$W_Y$
to understand its effect on the backscattered signal. In this work, we interpret (3.9) and the signal enhancement produced for specific
![]() $k_x$
as a consequence of beam focusing in the vicinity of a turning point, and not as due to forward scattering. The more the beam is focused (small
$k_x$
as a consequence of beam focusing in the vicinity of a turning point, and not as due to forward scattering. The more the beam is focused (small
![]() $W_Y$
), the more the signal is localised around the focusing region due to the local increase in the wave intensity, which takes place at a finite
$W_Y$
), the more the signal is localised around the focusing region due to the local increase in the wave intensity, which takes place at a finite
![]() $k_x$
(in the vicinity of, but not exactly at the turning point). This effect preferentially happens for small incident angles
$k_x$
(in the vicinity of, but not exactly at the turning point). This effect preferentially happens for small incident angles
![]() $\alpha _0$
, as was shown in § 2. The fact that the width
$\alpha _0$
, as was shown in § 2. The fact that the width
![]() $W_Y$
does not focus exactly at the turning point (see figures 3 and 4) results in the filter function peaking at a finite
$W_Y$
does not focus exactly at the turning point (see figures 3 and 4) results in the filter function peaking at a finite
![]() $k_x$
(recall that
$k_x$
(recall that
![]() $k_x=0$
corresponds to the turning point location).
$k_x=0$
corresponds to the turning point location).
With respect to the wavenumber resolution, (3.9) recovers previous calculations of the DBS wavenumber resolution (Lin et al. Reference Lin, Nazikian, Irby and Marmar2001; Hirsch et al. Reference Hirsch, Holzhauer, Baldzuhn and Kurzan2001; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012), which is derived here in the context of a beam-tracing model. Note the difference between
![]() $\Delta k_y$
in the lab frame, which is constant along the path in the particular case of the 2-D linear layer, and
$\Delta k_y$
in the lab frame, which is constant along the path in the particular case of the 2-D linear layer, and
![]() $\Delta k_{\mu 2}$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), which is perpendicular to the central ray propagation and depends strongly on the distance along the path. Equation (3.10) simplifies to
$\Delta k_{\mu 2}$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), which is perpendicular to the central ray propagation and depends strongly on the distance along the path. Equation (3.10) simplifies to
![]() $\Delta k_y = 2/\rho$
for the choice of
$\Delta k_y = 2/\rho$
for the choice of
![]() $\Psi _{yy0}$
made by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Note how the value
$\Psi _{yy0}$
made by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Note how the value
![]() $2/\rho$
is a lower limit to the diagnostic
$2/\rho$
is a lower limit to the diagnostic
![]() $k_y$
-wavenumber resolution. Interestingly, the wavenumber resolution
$k_y$
-wavenumber resolution. Interestingly, the wavenumber resolution
![]() $\Delta k_y$
depends on the incidence angle
$\Delta k_y$
depends on the incidence angle
![]() $\alpha _0$
for a given initial
$\alpha _0$
for a given initial
![]() $W_0$
,
$W_0$
,
![]() $R_{Y0}$
and a given
$R_{Y0}$
and a given
![]() $L$
. Inspecting (3.10) and using the expression for
$L$
. Inspecting (3.10) and using the expression for
![]() $\Psi _{yy0}$
in terms of
$\Psi _{yy0}$
in terms of
![]() $W_0$
and
$W_0$
and
![]() $R_{Y0}$
(Appendix A), we find that
$R_{Y0}$
(Appendix A), we find that
 \begin{align} \begin{alignedat}{2} & \Delta k_y^2 = 2 \cos ^2\alpha _0 \frac {K_0^2W_0^2}{K_0L} \left [ \left ( \frac {L}{R_{Y0}} + \frac {\sin ^2\alpha _0}{2\cos \alpha _0} \right )^2 + 4 \left ( \frac {K_0L}{K_0^2W_0^2} \right )^2 \right ] \frac {K_0}{L}. \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \Delta k_y^2 = 2 \cos ^2\alpha _0 \frac {K_0^2W_0^2}{K_0L} \left [ \left ( \frac {L}{R_{Y0}} + \frac {\sin ^2\alpha _0}{2\cos \alpha _0} \right )^2 + 4 \left ( \frac {K_0L}{K_0^2W_0^2} \right )^2 \right ] \frac {K_0}{L}. \end{alignedat} \end{align}
Equation (3.14) shows how
![]() $\Delta k_y$
can have a non-trivial dependence on
$\Delta k_y$
can have a non-trivial dependence on
![]() $\alpha _0$
, which should be taken into consideration when comparing the scattered power in DBS measurements and in numerical turbulence simulations via synthetic diagnostics.
$\alpha _0$
, which should be taken into consideration when comparing the scattered power in DBS measurements and in numerical turbulence simulations via synthetic diagnostics.
Equations (3.9), (3.10) and (3.12) are the bases for synthetic DBS diagnostics that can be readily applied to direct nonlinear gyrokinetic simulations of plasma turbulence. In that context, and borrowing notation from previous work (Ruiz et al. Reference Ruiz2022),
![]() $k_x$
and
$k_x$
and
![]() $k_y$
can be directly identified to the physical normal and binormal wavenumbers
$k_y$
can be directly identified to the physical normal and binormal wavenumbers
![]() $k_n$
and
$k_n$
and
![]() $k_b$
. The Cartesian
$k_b$
. The Cartesian
![]() $k_x$
employed here corresponds to the normal wavenumber component of the gyrokinetic simulation
$k_x$
employed here corresponds to the normal wavenumber component of the gyrokinetic simulation
![]() $k_x = k_n = \mathbf {k_\perp } \cdot {\hat{\mathbf{e}}}_{n}$
, where
$k_x = k_n = \mathbf {k_\perp } \cdot {\hat{\mathbf{e}}}_{n}$
, where
![]() ${\hat{\mathbf{e}}}_{n} = \nabla r/|\nabla r|$
is the unit vector normal to the flux surface identified by minor radius
${\hat{\mathbf{e}}}_{n} = \nabla r/|\nabla r|$
is the unit vector normal to the flux surface identified by minor radius
![]() $r$
. The Cartesian
$r$
. The Cartesian
![]() $k_y$
corresponds to the binormal wavenumber of gyrokinetic simulations
$k_y$
corresponds to the binormal wavenumber of gyrokinetic simulations
![]() $k_y = k_b = \mathbf {k_\perp } \cdot {\hat{\mathbf{e}}}_{b}$
, where
$k_y = k_b = \mathbf {k_\perp } \cdot {\hat{\mathbf{e}}}_{b}$
, where
![]() ${\hat{\mathbf{e}}}_{b} = {\hat{\mathbf{e}}}_{n} \times {\hat{\mathbf{b}}}$
is the binormal wavevector, perpendicular to the unit vector of the magnetic field
${\hat{\mathbf{e}}}_{b} = {\hat{\mathbf{e}}}_{n} \times {\hat{\mathbf{b}}}$
is the binormal wavevector, perpendicular to the unit vector of the magnetic field
![]() ${\hat{\mathbf{b}}}$
and to
${\hat{\mathbf{b}}}$
and to
![]() ${\hat{\mathbf{e}}}_{n}$
. Depending on the gyrokinetic code used,
${\hat{\mathbf{e}}}_{n}$
. Depending on the gyrokinetic code used,
![]() $k_n$
and
$k_n$
and
![]() $k_b$
might need to be mapped from internal code wavenumber definitions, examples of which are given by Ruiz et al. (Reference Ruiz2022).
$k_b$
might need to be mapped from internal code wavenumber definitions, examples of which are given by Ruiz et al. (Reference Ruiz2022).
4. Consequences of beam focusing for DBS measurements
The phenomenon of beam focusing affects the DBS signal localisation and wavenumber resolution, and it enhances the DBS signal in the vicinity of the beam focusing region, as shown by the filter function
![]() $|F_{x\mu }|^2 \propto 1/K_\mu W_{Y\mu }$
for the 2-D linear-layer problem in (3.11). This challenges the interpretation of ‘forward scattering’ provided by Gusakov & Surkov (Reference Gusakov and Surkov2004), Gusakov et al. (Reference Gusakov, Irzak and Popov2014) and Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) as the responsible mechanism for the DBS signal enhancement for decreasing launch angle
$|F_{x\mu }|^2 \propto 1/K_\mu W_{Y\mu }$
for the 2-D linear-layer problem in (3.11). This challenges the interpretation of ‘forward scattering’ provided by Gusakov & Surkov (Reference Gusakov and Surkov2004), Gusakov et al. (Reference Gusakov, Irzak and Popov2014) and Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) as the responsible mechanism for the DBS signal enhancement for decreasing launch angle
![]() $\alpha _0$
. In this section, we characterise the consequences of beam focusing on the DBS signal through the filter function
$\alpha _0$
. In this section, we characterise the consequences of beam focusing on the DBS signal through the filter function
![]() $|F_{x\mu }|^2$
for the 2-D linear-layer problem. We scan the possible initial conditions: incident angle
$|F_{x\mu }|^2$
for the 2-D linear-layer problem. We scan the possible initial conditions: incident angle
![]() $\alpha _0$
, initial width
$\alpha _0$
, initial width
![]() $W_{0}$
and initial radius of curvature
$W_{0}$
and initial radius of curvature
![]() $R_{Y0}$
. In what follows,
$R_{Y0}$
. In what follows,
![]() $K_\mu$
and
$K_\mu$
and
![]() $W_{Y\mu }$
are normalised to the initial conditions
$W_{Y\mu }$
are normalised to the initial conditions
![]() $K_0$
and
$K_0$
and
![]() $W_0$
, respectively.
$W_0$
, respectively.
4.1.
The 1-D filter function
 $|F_{x\mu }|^2$
$|F_{x\mu }|^2$
The filter function
![]() $|F_{x\mu }|^2$
in (3.11) provides the
$|F_{x\mu }|^2$
in (3.11) provides the
![]() $k_x$
-selectivity of the DBS power. This is tied to the localisation along the path: the scattering turbulent
$k_x$
-selectivity of the DBS power. This is tied to the localisation along the path: the scattering turbulent
![]() $k_x$
can be thought of as a parameter determining the location of scattering along the path
$k_x$
can be thought of as a parameter determining the location of scattering along the path
![]() $\tau _\mu$
, as
$\tau _\mu$
, as
![]() $\tau _\mu$
is related to the turbulent scattering
$\tau _\mu$
is related to the turbulent scattering
![]() $k_x$
via the Bragg condition for backscattering in (3.6), which is used to arrive at (3.13). The radial component
$k_x$
via the Bragg condition for backscattering in (3.6), which is used to arrive at (3.13). The radial component
![]() $K_{x\mu } = K_0(\cos \alpha _0 - \tau ^{\prime}_\mu )$
from (2.9) is a decreasing function of
$K_{x\mu } = K_0(\cos \alpha _0 - \tau ^{\prime}_\mu )$
from (2.9) is a decreasing function of
![]() $\tau ^{\prime}_\mu$
from the launch, becoming negative after the turning point (
$\tau ^{\prime}_\mu$
from the launch, becoming negative after the turning point (
![]() $K_{x\mu }=0$
, i.e.
$K_{x\mu }=0$
, i.e.
![]() $\tau ^{\prime}_\mu = \cos \alpha _0$
). The vertical component
$\tau ^{\prime}_\mu = \cos \alpha _0$
). The vertical component
![]() $K_y$
is constant, since the system is homogeneous in
$K_y$
is constant, since the system is homogeneous in
![]() $y$
. This means that
$y$
. This means that
![]() $K_\mu$
reaches its minimum at the turning point, which should enhance the DBS signal contribution at that location. As we saw in the previous section, the perpendicular beam width
$K_\mu$
reaches its minimum at the turning point, which should enhance the DBS signal contribution at that location. As we saw in the previous section, the perpendicular beam width
![]() $W_{Y\mu }$
has a tendency to focus, which should further enhance the DBS signal power. In this section, we separate the enhancement due to ray and the beam contributions in the filter function.
$W_{Y\mu }$
has a tendency to focus, which should further enhance the DBS signal power. In this section, we separate the enhancement due to ray and the beam contributions in the filter function.

Figure 5. Filter function
![]() $|F_{x\mu }|^2(\tau )/|F_0|^2 = K_0 W_0/K_\mu W_{Y\mu }$
and the corresponding ray component
$|F_{x\mu }|^2(\tau )/|F_0|^2 = K_0 W_0/K_\mu W_{Y\mu }$
and the corresponding ray component
![]() $K_0/K_\mu$
and beam component
$K_0/K_\mu$
and beam component
![]() $W_0/W_{Y\mu }$
for varying values of the incident launch angle
$W_0/W_{Y\mu }$
for varying values of the incident launch angle
![]() $\alpha _0$
, and fixed
$\alpha _0$
, and fixed
![]() $R_{Y0} = \infty$
and
$R_{Y0} = \infty$
and
![]() $W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. Note that in all cases, the filter function is predominantly affected by the beam term
$W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
. Note that in all cases, the filter function is predominantly affected by the beam term
![]() $1/W_{Y\mu }$
which represents the focusing.
$1/W_{Y\mu }$
which represents the focusing.
Figure 5 shows the ray (blue) and beam (red) components of
![]() $|F_{x\mu }|^2$
for varying incident angles
$|F_{x\mu }|^2$
for varying incident angles
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
$\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
![]() $ 80^{\circ }$
, and fixed
$ 80^{\circ }$
, and fixed
![]() $W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
and
$W_0 = 0.40(\lambda L)^{\frac {1}{2}}$
and
![]() $R_{Y0} = \infty$
(launch at the waist). For convenience, we normalise the filter function to its value at
$R_{Y0} = \infty$
(launch at the waist). For convenience, we normalise the filter function to its value at
![]() $\tau =0$
,
$\tau =0$
,
![]() $|F_0|^2$
. The filter functions correspond to some of the beam solutions in figure 3. For
$|F_0|^2$
. The filter functions correspond to some of the beam solutions in figure 3. For
![]() $\alpha _0=10^{\circ }$
, the filter function
$\alpha _0=10^{\circ }$
, the filter function
![]() $|F_{x\mu }|^2$
is strongly localised at the focus location, which almost matches the location of the turning point, or cutoff (maximum of the ray term in blue). The turning point, or cutoff, is represented in each figure by a vertical grey dotted line. Careful inspection shows that the focus location takes place in the vicinity but after the turning point
$|F_{x\mu }|^2$
is strongly localised at the focus location, which almost matches the location of the turning point, or cutoff (maximum of the ray term in blue). The turning point, or cutoff, is represented in each figure by a vertical grey dotted line. Careful inspection shows that the focus location takes place in the vicinity but after the turning point
![]() $\tau ^{\prime}_\mu = \cos \alpha _0$
for
$\tau ^{\prime}_\mu = \cos \alpha _0$
for
![]() $\alpha _0=10^{\circ }$
, consistent with beam focusing taking place after the turning point in figure 3. This shows that the contributions to the DBS power are predominantly from the vicinity (but after) the turning point for these initial conditions.
$\alpha _0=10^{\circ }$
, consistent with beam focusing taking place after the turning point in figure 3. This shows that the contributions to the DBS power are predominantly from the vicinity (but after) the turning point for these initial conditions.
For larger incident angles, the turning point takes place for smaller
![]() $\tau _\mu ^{\prime} = \cos \alpha _0$
, while the beam term peaks at larger
$\tau _\mu ^{\prime} = \cos \alpha _0$
, while the beam term peaks at larger
![]() $\tau _\mu ^{\prime}$
(beam focus takes place at larger
$\tau _\mu ^{\prime}$
(beam focus takes place at larger
![]() $\tau _\mu ^{\prime}$
): the ray and beam terms compete to yield a filter function that is less peaked and less localised around the focus location for increasing
$\tau _\mu ^{\prime}$
): the ray and beam terms compete to yield a filter function that is less peaked and less localised around the focus location for increasing
![]() $\alpha _0$
. The ray term (blue) decreases in amplitude for larger
$\alpha _0$
. The ray term (blue) decreases in amplitude for larger
![]() $\alpha _0$
, but less than the beam term (red), which decreases more. The beam term becomes broader in
$\alpha _0$
, but less than the beam term (red), which decreases more. The beam term becomes broader in
![]() $\tau _\mu ^{\prime}$
for larger angles. These effects make the signal more delocalised along the path. This can be clearly seen in figure 5(c). The localisation becomes broad for
$\tau _\mu ^{\prime}$
for larger angles. These effects make the signal more delocalised along the path. This can be clearly seen in figure 5(c). The localisation becomes broad for
![]() $\alpha _0=50^{\circ }$
, where beam focusing becomes less important in favour of contributions from
$\alpha _0=50^{\circ }$
, where beam focusing becomes less important in favour of contributions from
![]() $\tau ^{\prime}_\mu = 0$
. In figure 5, the initial condition is chosen to be at the waist
$\tau ^{\prime}_\mu = 0$
. In figure 5, the initial condition is chosen to be at the waist
![]() $W_{Y}(\tau =0)=W_0$
. In figure 7, we show the effect of the initial radius of curvature
$W_{Y}(\tau =0)=W_0$
. In figure 7, we show the effect of the initial radius of curvature
![]() $R_{Y0}$
on the filter function. An initially expanding beam (positive and finite
$R_{Y0}$
on the filter function. An initially expanding beam (positive and finite
![]() $R_{Y0}/L$
) is shown in figure 7 not to make a dramatic difference on
$R_{Y0}/L$
) is shown in figure 7 not to make a dramatic difference on
![]() $|F_{x\mu }|^2$
. For larger incident angles (
$|F_{x\mu }|^2$
. For larger incident angles (
![]() $\alpha _0 = 80^{\circ }$
), the filter peaks around
$\alpha _0 = 80^{\circ }$
), the filter peaks around
![]() $\tau = 0$
, corresponding to the waist initial condition of figure 5 (figure 7 shows that the behaviour is qualitatively similar for different initial
$\tau = 0$
, corresponding to the waist initial condition of figure 5 (figure 7 shows that the behaviour is qualitatively similar for different initial
![]() $R_{Y0}$
). Therefore, for large incident angles, the DBS signal becomes delocalised with predominant contributions before and after the turning point (figures 5 and 7).
$R_{Y0}$
). Therefore, for large incident angles, the DBS signal becomes delocalised with predominant contributions before and after the turning point (figures 5 and 7).

Figure 6. Filter function
![]() $|F_{x\mu }|^2(\tau )/|F_0|^2 = K_0 W_0/K_\mu W_{Y\mu }$
and the corresponding ray component
$|F_{x\mu }|^2(\tau )/|F_0|^2 = K_0 W_0/K_\mu W_{Y\mu }$
and the corresponding ray component
![]() $K_0/K_\mu$
and beam component
$K_0/K_\mu$
and beam component
![]() $W_0/W_{Y\mu }$
for varying values of the initial width
$W_0/W_{Y\mu }$
for varying values of the initial width
![]() $W_0 = 0.13, 0.40, 1.26(\lambda L)^{\frac {1}{2}}$
, and fixed
$W_0 = 0.13, 0.40, 1.26(\lambda L)^{\frac {1}{2}}$
, and fixed
![]() $R_{Y0} = \infty$
and
$R_{Y0} = \infty$
and
![]() $\alpha _0 = 30^{\circ }$
. Note that in all cases, the filter function is predominantly affected by the beam term
$\alpha _0 = 30^{\circ }$
. Note that in all cases, the filter function is predominantly affected by the beam term
![]() $1/W_{Y\mu }$
which represents the focusing.
$1/W_{Y\mu }$
which represents the focusing.

Figure 7. Values of the filter function
![]() $|F_{x\mu }|^2/|F_0|^2$
for varying incident angles
$|F_{x\mu }|^2/|F_0|^2$
for varying incident angles
![]() $\alpha _0$
and fixed initial
$\alpha _0$
and fixed initial
![]() $W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
as a function of the turbulent, selected
$W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
as a function of the turbulent, selected
![]() $k_x$
component. For small incident angle
$k_x$
component. For small incident angle
![]() $\alpha _0=10^{\circ }$
, the filter is strongly peaked near
$\alpha _0=10^{\circ }$
, the filter is strongly peaked near
![]() $k_x = 0$
, consistent with the signal being strongly localised near the turning point region. The signal is in fact sensitive to slightly positive
$k_x = 0$
, consistent with the signal being strongly localised near the turning point region. The signal is in fact sensitive to slightly positive
![]() $k_x\gt 0$
, which corresponds to a focusing slightly after the turning point. For
$k_x\gt 0$
, which corresponds to a focusing slightly after the turning point. For
![]() $\alpha _0=30^{\circ }$
, the peak near
$\alpha _0=30^{\circ }$
, the peak near
![]() $k_x=0$
decreases and shifts to larger
$k_x=0$
decreases and shifts to larger
![]() $k_x$
values, meaning that the signal starts getting important contributions from finite
$k_x$
values, meaning that the signal starts getting important contributions from finite
![]() $k_x$
turbulent fluctuations away from the turning point. For
$k_x$
turbulent fluctuations away from the turning point. For
![]() $\alpha _0=50^{\circ }$
, the peak has almost disappeared and the signal receives close-to-uniform contributions in the range of
$\alpha _0=50^{\circ }$
, the peak has almost disappeared and the signal receives close-to-uniform contributions in the range of
![]() $-1 \lesssim k_x/K_0 \lesssim 2$
, corresponding to a highly delocalised signal along the beam path. For
$-1 \lesssim k_x/K_0 \lesssim 2$
, corresponding to a highly delocalised signal along the beam path. For
![]() $\alpha _0 = 80^{\circ }$
, the beam expands for most of its path and the filter function approaches the vacuum solution.
$\alpha _0 = 80^{\circ }$
, the beam expands for most of its path and the filter function approaches the vacuum solution.
Figure 6 shows the ray (blue) and beam (red) components of
![]() $|F_{x\mu }|^2$
for different values of the initial width
$|F_{x\mu }|^2$
for different values of the initial width
![]() $W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40$
and
$W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40$
and
![]() $1.26$
, and fixed incident angle
$1.26$
, and fixed incident angle
![]() $\alpha _0 = 30^{\circ }$
and
$\alpha _0 = 30^{\circ }$
and
![]() $R_{Y0} = \infty$
(launch at the waist). The filter functions in figure 6 correspond to some of the beam solutions in figure 4. In this case, the ray term remains constant. The beam term is narrowest around the initial launch (waist) and around the focusing point for small initial width
$R_{Y0} = \infty$
(launch at the waist). The filter functions in figure 6 correspond to some of the beam solutions in figure 4. In this case, the ray term remains constant. The beam term is narrowest around the initial launch (waist) and around the focusing point for small initial width
![]() $W_0=0.13 (\lambda L)^{\frac {1}{2}}$
. This is because a small initial width produces rapid expansion of the beam (see figure 4), which gives negligible contributions to the beam term outside the waist and focus point. This suggests a very localised contribution to the DBS power from the vicinity of the focus point as well as the plasma edge (if enough fluctuations are present). For initial width
$W_0=0.13 (\lambda L)^{\frac {1}{2}}$
. This is because a small initial width produces rapid expansion of the beam (see figure 4), which gives negligible contributions to the beam term outside the waist and focus point. This suggests a very localised contribution to the DBS power from the vicinity of the focus point as well as the plasma edge (if enough fluctuations are present). For initial width
![]() $W_0=0.40(\lambda L)^{\frac {1}{2}}$
, the location of the peak in
$W_0=0.40(\lambda L)^{\frac {1}{2}}$
, the location of the peak in
![]() $|F_{x\mu }|^2$
is similar to that for
$|F_{x\mu }|^2$
is similar to that for
![]() $W_0 = 0.13 (\lambda L)^{\frac {1}{2}}$
, but the filter function becomes broader, suggesting that the beam focusing is slower and takes place over a larger region, as shown in figure 4. For
$W_0 = 0.13 (\lambda L)^{\frac {1}{2}}$
, but the filter function becomes broader, suggesting that the beam focusing is slower and takes place over a larger region, as shown in figure 4. For
![]() $W_0=1.26(\lambda L)^{\frac {1}{2}}$
, the filter function maximum has increased in value (beam focuses more) and has a peak as broad as the filter function for
$W_0=1.26(\lambda L)^{\frac {1}{2}}$
, the filter function maximum has increased in value (beam focuses more) and has a peak as broad as the filter function for
![]() $W_0 = 0.4 (\lambda L)^{\frac {1}{2}}$
. Interestingly, in this case, the filter function
$W_0 = 0.4 (\lambda L)^{\frac {1}{2}}$
. Interestingly, in this case, the filter function
![]() $|F_{x\mu }|^2$
does not exhibit an initial decrease after the launch. This is because, in this condition, the beam does not initially expand following the launch, but only contracts from launch to the focus location (see black line in figure 4
c). Moreover, the beam focuses closer to the turning point than for
$|F_{x\mu }|^2$
does not exhibit an initial decrease after the launch. This is because, in this condition, the beam does not initially expand following the launch, but only contracts from launch to the focus location (see black line in figure 4
c). Moreover, the beam focuses closer to the turning point than for
![]() $W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.4$
.
$W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.4$
.
Figures 3–7 show that the beam focusing in
![]() $W_Y$
tends to take place close to but after the turning point (
$W_Y$
tends to take place close to but after the turning point (
![]() $K_{x\mu }=0, \tau ^{\prime}_\mu =\cos \alpha _0$
) depending on the initial conditions for the incident angle
$K_{x\mu }=0, \tau ^{\prime}_\mu =\cos \alpha _0$
) depending on the initial conditions for the incident angle
![]() $\alpha _0$
, width
$\alpha _0$
, width
![]() $W_0/(\lambda L)^{\frac {1}{2}}$
and especially on the phase front radius of curvature
$W_0/(\lambda L)^{\frac {1}{2}}$
and especially on the phase front radius of curvature
![]() $R_{Y0}$
. This challenges the common belief that the DBS signal is always most sensitive at the turning point and has important consequences for interpreting the DBS scattered power.
$R_{Y0}$
. This challenges the common belief that the DBS signal is always most sensitive at the turning point and has important consequences for interpreting the DBS scattered power.
It is equally instructive to characterise the filter function in terms of the turbulent scattered
![]() $k_x$
. Note that negative
$k_x$
. Note that negative
![]() $k_x$
corresponds to scattering from the beam in its first pass from launch towards the turning point, and positive
$k_x$
corresponds to scattering from the beam in its first pass from launch towards the turning point, and positive
![]() $k_x$
to scattering from the beam in its return journey away from the turning point. Figure 7 shows the variation of the filter function
$k_x$
to scattering from the beam in its return journey away from the turning point. Figure 7 shows the variation of the filter function
![]() $|F_{x\mu }|^2$
for different incident angles
$|F_{x\mu }|^2$
for different incident angles
![]() $\alpha _0$
, different initial radii of curvature
$\alpha _0$
, different initial radii of curvature
![]() $R_{Y0}$
and
$R_{Y0}$
and
![]() $W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
as a function of the turbulent scattered
$W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
as a function of the turbulent scattered
![]() $k_x$
. For
$k_x$
. For
![]() $\alpha _0=10^{\circ }$
,
$\alpha _0=10^{\circ }$
,
![]() $|F_{x\mu }|^2$
is strongly peaked at
$|F_{x\mu }|^2$
is strongly peaked at
![]() $k_x=0$
. This means that the DBS signal is strongly localised near the turning point region and predominantly sensitive to fluctuations with
$k_x=0$
. This means that the DBS signal is strongly localised near the turning point region and predominantly sensitive to fluctuations with
![]() $k_x \approx 0$
. For
$k_x \approx 0$
. For
![]() $\alpha _0=30^{\circ }$
, the filter peak shifts towards larger
$\alpha _0=30^{\circ }$
, the filter peak shifts towards larger
![]() $k_x$
. For even larger
$k_x$
. For even larger
![]() $\alpha _0=50^{\circ }$
, the filter is sensitive almost uniformly to
$\alpha _0=50^{\circ }$
, the filter is sensitive almost uniformly to
![]() $-1 \lesssim k_x/K_0 \lesssim 2$
, with peaks of the filter function at both positive and negative
$-1 \lesssim k_x/K_0 \lesssim 2$
, with peaks of the filter function at both positive and negative
![]() $k_x$
, and surprisingly a dip in the vicinity of
$k_x$
, and surprisingly a dip in the vicinity of
![]() $k_x=0$
. This suggests that the DBS power is sensitive predominantly to specific values of
$k_x=0$
. This suggests that the DBS power is sensitive predominantly to specific values of
![]() $k_x$
, with a subdominant contribution from
$k_x$
, with a subdominant contribution from
![]() $k_x=0$
. For
$k_x=0$
. For
![]() $\alpha _0=80^{\circ }$
, the beam follows closely vacuum propagation and the filter has contributions from small
$\alpha _0=80^{\circ }$
, the beam follows closely vacuum propagation and the filter has contributions from small
![]() $k_x/K_0$
near
$k_x/K_0$
near
![]() $0$
, but this time originating near
$0$
, but this time originating near
![]() $\tau =0$
(near the vacuum beam-waist, or edge of the plasma in a real experiment) and decays for larger
$\tau =0$
(near the vacuum beam-waist, or edge of the plasma in a real experiment) and decays for larger
![]() $k_x$
. The beam expands for most of its path and the filter function approaches the vacuum solution (black dashed line).
$k_x$
. The beam expands for most of its path and the filter function approaches the vacuum solution (black dashed line).

Figure 8. Values of the filter function
![]() $|F_{x\mu }|^2/|F_0|^2$
for varying initial width
$|F_{x\mu }|^2/|F_0|^2$
for varying initial width
![]() $W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.40, 1.26$
and fixed
$W_0/(\lambda L)^{\frac {1}{2}} = 0.13, 0.40, 1.26$
and fixed
![]() $\alpha _0 = 30^{\circ }$
as a function of the turbulent, selected
$\alpha _0 = 30^{\circ }$
as a function of the turbulent, selected
![]() $k_x$
. For small initial
$k_x$
. For small initial
![]() $W_0$
, the filter is strongly peaked at two values of
$W_0$
, the filter is strongly peaked at two values of
![]() $k_x$
: one negative that corrresponds to the entrance to the plasma, and one positive from the beam focusing. For small
$k_x$
: one negative that corrresponds to the entrance to the plasma, and one positive from the beam focusing. For small
![]() $W_0$
, the filter is also independent of the initial condition
$W_0$
, the filter is also independent of the initial condition
![]() $R_{Y0}$
. For
$R_{Y0}$
. For
![]() $W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
, the filter is dominated by a peak of amplitude and location similar to those of the peak due to focusing for small
$W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
, the filter is dominated by a peak of amplitude and location similar to those of the peak due to focusing for small
![]() $W_0$
, but broader. For
$W_0$
, but broader. For
![]() $W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
, the peak in
$W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
, the peak in
![]() $k_x$
stays broad and shifts towards
$k_x$
stays broad and shifts towards
![]() $k_x=0$
for launch near the waist (large
$k_x=0$
for launch near the waist (large
![]() $|R_{Y0}/L|$
).
$|R_{Y0}/L|$
).
Figure 8 shows the corresponding filter function for varying
![]() $W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40$
and
$W_0 / (\lambda L)^{\frac {1}{2}} = 0.13, 0.40$
and
![]() $1.26$
, different radii of curvature and fixed initial angle
$1.26$
, different radii of curvature and fixed initial angle
![]() $\alpha _0=30^{\circ }$
. The behaviour of the filter function for small
$\alpha _0=30^{\circ }$
. The behaviour of the filter function for small
![]() $W_0$
can be understood from figure 4. For small initial
$W_0$
can be understood from figure 4. For small initial
![]() $W_0$
, the filter is strongly peaked at two different values of
$W_0$
, the filter is strongly peaked at two different values of
![]() $k_x$
and is independent of the initial condition
$k_x$
and is independent of the initial condition
![]() $R_{Y0}$
, consistent with the signal being strongly localised at the plasma entrance and near the turning point region. For
$R_{Y0}$
, consistent with the signal being strongly localised at the plasma entrance and near the turning point region. For
![]() $W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
, the filter is dominated by a peak with amplitude and location similar to those of the peak due to focusing for small
$W_0 = 0.40 (\lambda L)^{\frac {1}{2}}$
, the filter is dominated by a peak with amplitude and location similar to those of the peak due to focusing for small
![]() $W_0$
, but broader, and hence the signal gets enhanced contributions from turbulent fluctuations away from the focusing region, depending on the initial condition
$W_0$
, but broader, and hence the signal gets enhanced contributions from turbulent fluctuations away from the focusing region, depending on the initial condition
![]() $R_{Y0}$
. For
$R_{Y0}$
. For
![]() $W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
, the peak in
$W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
, the peak in
![]() $k_x$
stays broad and shifts towards
$k_x$
stays broad and shifts towards
![]() $k_x=0$
for launch near the waist (large
$k_x=0$
for launch near the waist (large
![]() $|R_{Y0}/L|$
). The small
$|R_{Y0}/L|$
). The small
![]() $|R_{Y0}/L|$
cases are different, exhibiting distinctive narrow peaks that even appear twice for
$|R_{Y0}/L|$
cases are different, exhibiting distinctive narrow peaks that even appear twice for
![]() $R_{Y0}/L=-0.5$
, consistent with two consecutive focusing regions, as in figure 4.
$R_{Y0}/L=-0.5$
, consistent with two consecutive focusing regions, as in figure 4.
4.2. Predictions of the measured turbulent spectra
Throughout this manuscript, we have focused on describing the dependence of the filter function
![]() $|F_{x\mu }|^2$
on experimentally relevant initial values for
$|F_{x\mu }|^2$
on experimentally relevant initial values for
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $W_0$
and
$W_0$
and
![]() $R_{Y0}$
. We should note, however, that the intrinsic power spectrum of the turbulence itself has a direct impact on the measurement. The turbulent spectrum is generally a decreasing function of
$R_{Y0}$
. We should note, however, that the intrinsic power spectrum of the turbulence itself has a direct impact on the measurement. The turbulent spectrum is generally a decreasing function of
![]() $k_x$
, as demonstrated by direct numerical gyrokinetic turbulence simulations. In conditions where the filter function predominantly selects large
$k_x$
, as demonstrated by direct numerical gyrokinetic turbulence simulations. In conditions where the filter function predominantly selects large
![]() $k_x$
(finite to large
$k_x$
(finite to large
![]() $\alpha _0$
), the turbulence spectrum in
$\alpha _0$
), the turbulence spectrum in
![]() $k_x$
should be taken into account to understand the dominant
$k_x$
should be taken into account to understand the dominant
![]() $k_x$
contributing to the backscattering signal. In this section, we apply what we have learned about the filter function
$k_x$
contributing to the backscattering signal. In this section, we apply what we have learned about the filter function
![]() $|F_{x\mu }|^2$
in the beam-tracing model and use it to understand its effect on the DBS backscattered power from a realistic density-fluctuation spectrum.
$|F_{x\mu }|^2$
in the beam-tracing model and use it to understand its effect on the DBS backscattered power from a realistic density-fluctuation spectrum.
We use the electron-density-fluctuation wavenumber power spectrum
![]() $ \langle | \delta \hat {n}(k_x, k_y)|^2 \rangle _T$
obtained from nonlinear gyrokinetic simulations resolving strongly developed ETG turbulence in NSTX, which was examined by Ruiz et al. (Reference Ruiz2015, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith, Loureiro, Holland and Domier2019, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Holland2020
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollanda
,
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollandb
); Ren et al. (Reference Ren2020); Ruiz et al. (Reference Ruiz2022); Guttenfelder et al. (Reference Guttenfelder2022). The turbulent spectrum can be approximated by the following shape:
$ \langle | \delta \hat {n}(k_x, k_y)|^2 \rangle _T$
obtained from nonlinear gyrokinetic simulations resolving strongly developed ETG turbulence in NSTX, which was examined by Ruiz et al. (Reference Ruiz2015, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith, Loureiro, Holland and Domier2019, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Holland2020
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollanda
,
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollandb
); Ren et al. (Reference Ren2020); Ruiz et al. (Reference Ruiz2022); Guttenfelder et al. (Reference Guttenfelder2022). The turbulent spectrum can be approximated by the following shape:
 \begin{align} \frac {\big\langle |\delta \hat {n} (k_x, k_y) |^2 \big\rangle _T}{n^2} \sim \frac {A}{1 + \big | \frac {k_x}{w_{k_x} }\big |^{\zeta } + \big | \frac {k_y - k_{y*}}{w_{k_y} } \big |^{\eta } }. \end{align}
\begin{align} \frac {\big\langle |\delta \hat {n} (k_x, k_y) |^2 \big\rangle _T}{n^2} \sim \frac {A}{1 + \big | \frac {k_x}{w_{k_x} }\big |^{\zeta } + \big | \frac {k_y - k_{y*}}{w_{k_y} } \big |^{\eta } }. \end{align}
This expression is fitted to the specific strongly driven ETG simulations that we have mentioned above (Ruiz et al. Reference Ruiz2022) to find:
![]() $\zeta \approx 3.14, \eta \approx 3.19, w_{k_x} \rho _s \approx 0.89, w_{k_y}\rho _s \approx 4.09, k_{y*}\rho _s \approx 6.53, A \approx 1.18 \ 10^{-6}$
(here
$\zeta \approx 3.14, \eta \approx 3.19, w_{k_x} \rho _s \approx 0.89, w_{k_y}\rho _s \approx 4.09, k_{y*}\rho _s \approx 6.53, A \approx 1.18 \ 10^{-6}$
(here
![]() $\rho _s$
is evaluated at the cutoff of the hypothetical DBS experiment). Ruiz et al. (Reference Ruiz2022) represented the fluctuation spectra in terms of the normal and binormal wavenumber components
$\rho _s$
is evaluated at the cutoff of the hypothetical DBS experiment). Ruiz et al. (Reference Ruiz2022) represented the fluctuation spectra in terms of the normal and binormal wavenumber components
![]() $k_n$
and
$k_n$
and
![]() $k_b$
perpendicular to the magnetic field, which can be easily calculated from the internal wavenumber components in a gyrokinetic code. The normal and binormal components correspond to the Cartesian
$k_b$
perpendicular to the magnetic field, which can be easily calculated from the internal wavenumber components in a gyrokinetic code. The normal and binormal components correspond to the Cartesian
![]() $k_x$
and
$k_x$
and
![]() $k_y$
employed throughout this manuscript, as we have explained at the end of § 3. Importantly, from here on, we assume that the turbulent spectrum is uniform in space, that is, the parameters
$k_y$
employed throughout this manuscript, as we have explained at the end of § 3. Importantly, from here on, we assume that the turbulent spectrum is uniform in space, that is, the parameters
![]() $A, \zeta , \eta , w_{k_x}, w_{k_y}$
and
$A, \zeta , \eta , w_{k_x}, w_{k_y}$
and
![]() $k_{y*}$
are assumed to be constant throughout the whole plasma volume through which the beam propagates.
$k_{y*}$
are assumed to be constant throughout the whole plasma volume through which the beam propagates.

Figure 9. (a) Values of the normalised beam width
![]() $W_Y/W_0$
along the path
$W_Y/W_0$
along the path
![]() $\tau$
for varying values of the incident angle
$\tau$
for varying values of the incident angle
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $W_0 \approx 1.26(\lambda L)^{\frac {1}{2}}$
and
$W_0 \approx 1.26(\lambda L)^{\frac {1}{2}}$
and
![]() $R_{Y0}/L = 0.5$
. The curves are plotted for the values of
$R_{Y0}/L = 0.5$
. The curves are plotted for the values of
![]() $\tau$
in which the beam is traversing the plasma slab,
$\tau$
in which the beam is traversing the plasma slab,
![]() $x\gt 0$
. We assume vacuum for
$x\gt 0$
. We assume vacuum for
![]() $x\lt 0$
and the beam is launched at
$x\lt 0$
and the beam is launched at
![]() $x=0$
. (b) Corresponding filter function
$x=0$
. (b) Corresponding filter function
![]() $|F_{x\mu }|^2/|F_0|^2 = {K_0 W_0}/{ K_\mu W_{Y\mu } }$
plotted as a function of the scattered turbulent
$|F_{x\mu }|^2/|F_0|^2 = {K_0 W_0}/{ K_\mu W_{Y\mu } }$
plotted as a function of the scattered turbulent
![]() $k_x$
within the plasma slab, that is, for
$k_x$
within the plasma slab, that is, for
![]() $|k_x/K_0 \cos \alpha _0| \lt 2$
.
$|k_x/K_0 \cos \alpha _0| \lt 2$
.
DBS experiments routinely vary the angle of incidence
![]() $\alpha _0$
to select different wavenumbers from the turbulence spectrum. In what follows, we show how the beam width
$\alpha _0$
to select different wavenumbers from the turbulence spectrum. In what follows, we show how the beam width
![]() $W_Y$
, the filter function
$W_Y$
, the filter function
![]() $|F_{x\mu }|^2$
and ultimately the measured turbulence spectrum are impacted by varying
$|F_{x\mu }|^2$
and ultimately the measured turbulence spectrum are impacted by varying
![]() $\alpha _0$
.
$\alpha _0$
.
Figure 9(a) shows the normalised beam width
![]() $W_Y/W_0$
from the beam-tracing equations as a function of
$W_Y/W_0$
from the beam-tracing equations as a function of
![]() $\tau$
for a range of incident angles
$\tau$
for a range of incident angles
![]() $\alpha _0 = (10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ })$
,
$\alpha _0 = (10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ })$
,
![]() $W_0 = 1.26(\lambda L)^{\frac {1}{2}}$
and
$W_0 = 1.26(\lambda L)^{\frac {1}{2}}$
and
![]() $R_{Y0}/L = 0.5$
. The beams in figure 9 have the same initial frequency
$R_{Y0}/L = 0.5$
. The beams in figure 9 have the same initial frequency
![]() $\Omega$
and reach a turning point location at
$\Omega$
and reach a turning point location at
![]() $x=L_n = L\cos ^2\alpha _0$
(see figure 1). Figure 9(a) exhibits beam focusing for
$x=L_n = L\cos ^2\alpha _0$
(see figure 1). Figure 9(a) exhibits beam focusing for
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }$
within the plasma while the beam focusing takes place outside the plasma for
$\alpha _0 = 10^{\circ }, 30^{\circ }$
within the plasma while the beam focusing takes place outside the plasma for
![]() $\alpha _0 = 50^{\circ }$
. Both the value of the minimum beam width and the focusing location increase with
$\alpha _0 = 50^{\circ }$
. Both the value of the minimum beam width and the focusing location increase with
![]() $\alpha _0$
in this particular case.
$\alpha _0$
in this particular case.
Figure 9(b) shows the DBS filter function
![]() $|F_{x\mu }|^2$
corresponding to figure 9(a) plotted as a function of the turbulent scattered
$|F_{x\mu }|^2$
corresponding to figure 9(a) plotted as a function of the turbulent scattered
![]() $k_x$
normalised to
$k_x$
normalised to
![]() $K_0\cos \alpha _0$
. The scattered
$K_0\cos \alpha _0$
. The scattered
![]() $k_x$
at every
$k_x$
at every
![]() $\tau$
location is computed using the Bragg condition for backscattering written in Cartesian coordinates,
$\tau$
location is computed using the Bragg condition for backscattering written in Cartesian coordinates,
![]() $k_x = - 2 K_{x\mu } = - 2 K_0 (\cos \alpha _0 - \tau ^{\prime}_\mu )$
(see § 3 and Appendix B). The turning point takes place where
$k_x = - 2 K_{x\mu } = - 2 K_0 (\cos \alpha _0 - \tau ^{\prime}_\mu )$
(see § 3 and Appendix B). The turning point takes place where
![]() $K_{x\mu }=0$
, i.e.
$K_{x\mu }=0$
, i.e.
![]() $\tau ^{\prime}_\mu =\cos \alpha _0$
. Note how the filter function peaks closer to
$\tau ^{\prime}_\mu =\cos \alpha _0$
. Note how the filter function peaks closer to
![]() $k_x=0$
for decreasing
$k_x=0$
for decreasing
![]() $\alpha _0$
, corresponding to the beam focusing location approaching the turning point for small angles. The intensity of the enhancement decreases for increasing
$\alpha _0$
, corresponding to the beam focusing location approaching the turning point for small angles. The intensity of the enhancement decreases for increasing
![]() $\alpha _0$
. The dominant
$\alpha _0$
. The dominant
![]() $k_x$
contributing to scattering is always positive
$k_x$
contributing to scattering is always positive
![]() $k_x\gt 0$
in this situation, which means that the signal is predominantly originating from plasma locations after the turning point. Note how this depends on the initial condition: figure 4(c) shows how the beam focusing can take place arbitrarily close to the turning point for the same
$k_x\gt 0$
in this situation, which means that the signal is predominantly originating from plasma locations after the turning point. Note how this depends on the initial condition: figure 4(c) shows how the beam focusing can take place arbitrarily close to the turning point for the same
![]() $\alpha _0=30^{\circ }$
and
$\alpha _0=30^{\circ }$
and
![]() $W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
values but different
$W_0 = 1.26 (\lambda L)^{\frac {1}{2}}$
values but different
![]() $R_{Y0}$
. Increasing values of
$R_{Y0}$
. Increasing values of
![]() $\alpha _0$
will move the filter function localisation of the DBS signal further and further away from the turning point, reaching the plasma exit for
$\alpha _0$
will move the filter function localisation of the DBS signal further and further away from the turning point, reaching the plasma exit for
![]() $\alpha _0 \approx 50^{\circ }$
in these conditions (see red line in figures 9
a and 9
b).
$\alpha _0 \approx 50^{\circ }$
in these conditions (see red line in figures 9
a and 9
b).

Figure 10. Density-fluctuation power
![]() $\langle |\delta \hat {n}|^2 \rangle _T$
and the product of the density-fluctuation power and the filter function
$\langle |\delta \hat {n}|^2 \rangle _T$
and the product of the density-fluctuation power and the filter function
![]() $\langle |\delta \hat {n}|^2 \rangle _T |F_{x\mu }|^2/|F_0|^2$
as a function of the normalised scattered turbulent radial wavenumber
$\langle |\delta \hat {n}|^2 \rangle _T |F_{x\mu }|^2/|F_0|^2$
as a function of the normalised scattered turbulent radial wavenumber
![]() $k_x\rho _s$
for different values of the scattered turbulence
$k_x\rho _s$
for different values of the scattered turbulence
![]() $k_{y0}\rho _s = -2K_{0}\rho _s \sin \alpha _0$
. The different
$k_{y0}\rho _s = -2K_{0}\rho _s \sin \alpha _0$
. The different
![]() $\alpha _0 = (10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ })$
correspond to scattered wavenumbers
$\alpha _0 = (10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ })$
correspond to scattered wavenumbers
![]() $k_{y0}\rho _s = -(1.50, 4.92, 10.15, 48.29)$
. Solid lines correspond to
$k_{y0}\rho _s = -(1.50, 4.92, 10.15, 48.29)$
. Solid lines correspond to
![]() $k_x \gt 0$
, while dashed lines correspond to
$k_x \gt 0$
, while dashed lines correspond to
![]() $k_x \lt 0$
. The red curve shows that the beam focusing has a strong effect in the measurement
$k_x \lt 0$
. The red curve shows that the beam focusing has a strong effect in the measurement
![]() $k_x$
selection for
$k_x$
selection for
![]() $\alpha _0 \lesssim 30^{\circ }{-}40^{\circ }$
, while the effect becomes negligible for
$\alpha _0 \lesssim 30^{\circ }{-}40^{\circ }$
, while the effect becomes negligible for
![]() $\alpha _0 \gtrsim 40^{\circ }$
.
$\alpha _0 \gtrsim 40^{\circ }$
.

Figure 11. (a) Integrated filter function
![]() $\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
for the scattered
$\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
for the scattered
![]() $k_x$
within the plasma (
$k_x$
within the plasma (
![]() $|k_x/K_0| \lt 2\cos \alpha _0$
). Note how the integrated weight
$|k_x/K_0| \lt 2\cos \alpha _0$
). Note how the integrated weight
![]() $\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
is not constant, meaning that the filter function can affect the measured DBS
$\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
is not constant, meaning that the filter function can affect the measured DBS
![]() $k_y$
spectrum. (b) Turbulent spectrum
$k_y$
spectrum. (b) Turbulent spectrum
![]() $\langle |\delta \hat {n}|^2(k_x=0, k_y) \rangle _T$
(black),
$\langle |\delta \hat {n}|^2(k_x=0, k_y) \rangle _T$
(black),
![]() $k_x$
-integrated spectrum
$k_x$
-integrated spectrum
![]() $\int \text {d}k_x\rho _s \langle |\delta \hat {n}(k_x, k_y)|^2 \rangle _T$
(magenta) and synthetic DBS spectrum
$\int \text {d}k_x\rho _s \langle |\delta \hat {n}(k_x, k_y)|^2 \rangle _T$
(magenta) and synthetic DBS spectrum
![]() $\int \text {d}k_x\rho _s ( |F_{x\mu }|^2 /|F_0|^2 ) \langle | \delta \hat {n} |^2 \rangle _T (k_x, k_{y})$
(blue) as a function of
$\int \text {d}k_x\rho _s ( |F_{x\mu }|^2 /|F_0|^2 ) \langle | \delta \hat {n} |^2 \rangle _T (k_x, k_{y})$
(blue) as a function of
![]() $k_y$
of the turbulence. The turbulence spectrum has been fitted to a gyrokinetic simulation (Ruiz et al. Reference Ruiz2022). Note how the predicted DBS measurement is not able to capture the spectral peak of the turbulent spectrum (injection scale), but it is able to quantitatively reproduce the spectral exponent of the
$k_y$
of the turbulence. The turbulence spectrum has been fitted to a gyrokinetic simulation (Ruiz et al. Reference Ruiz2022). Note how the predicted DBS measurement is not able to capture the spectral peak of the turbulent spectrum (injection scale), but it is able to quantitatively reproduce the spectral exponent of the
![]() $k_x$
-integrated spectrum. The red dots indicate the specific angles
$k_x$
-integrated spectrum. The red dots indicate the specific angles
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ }$
given for reference.
$\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }, 80^{\circ }$
given for reference.
Next, we quantify the combined effect of the filter function and its dependence on
![]() $k_x$
, in conjunction with a realistic, power-law turbulence spectrum. In figures 10 and 11, we normalise
$k_x$
, in conjunction with a realistic, power-law turbulence spectrum. In figures 10 and 11, we normalise
![]() $k_x$
,
$k_x$
,
![]() $k_y$
and the initial wavenumber magnitude
$k_y$
and the initial wavenumber magnitude
![]() $K_0$
to the local ion sound gyroradius at the cutoff
$K_0$
to the local ion sound gyroradius at the cutoff
![]() $\rho _s = c_s/\Omega _D$
, where
$\rho _s = c_s/\Omega _D$
, where
![]() $c_s = (T_e/m_D)^{1/2}$
is the local ion sound speed,
$c_s = (T_e/m_D)^{1/2}$
is the local ion sound speed,
![]() $m_D$
the deuterium mass and
$m_D$
the deuterium mass and
![]() $\Omega _D = eB/m_D$
is the deuterium gyro-frequency. Using the relation
$\Omega _D = eB/m_D$
is the deuterium gyro-frequency. Using the relation
![]() $\Omega = \omega _{pe0}/\cos \alpha _0$
between
$\Omega = \omega _{pe0}/\cos \alpha _0$
between
![]() $\Omega$
and the local value of the electron plasma frequency at the cutoff
$\Omega$
and the local value of the electron plasma frequency at the cutoff
![]() $\omega _{pe0}$
(see § 2.3), we have
$\omega _{pe0}$
(see § 2.3), we have
![]() $K_0\rho _s = (\beta _e m_D/2m_e)^{1/2}/\cos \alpha _0 \approx 4.26/\cos \alpha _0$
, where
$K_0\rho _s = (\beta _e m_D/2m_e)^{1/2}/\cos \alpha _0 \approx 4.26/\cos \alpha _0$
, where
![]() $\beta _e \approx 1\, \%$
is the electron beta using the local magnetic field, electron density and temperature of the NSTX experiment analysed by Ruiz et al. (Reference Ruiz2015, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith, Loureiro, Holland and Domier2019, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Holland2020
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollanda
,
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollandb
); Ren et al. (Reference Ren2020); Ruiz et al. (Reference Ruiz2022); Guttenfelder et al. (Reference Guttenfelder2022).
$\beta _e \approx 1\, \%$
is the electron beta using the local magnetic field, electron density and temperature of the NSTX experiment analysed by Ruiz et al. (Reference Ruiz2015, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith, Loureiro, Holland and Domier2019, Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Holland2020
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollanda
,
Reference Ruiz, Guttenfelder, White, Howard, Candy, Ren, Smith and Hollandb
); Ren et al. (Reference Ren2020); Ruiz et al. (Reference Ruiz2022); Guttenfelder et al. (Reference Guttenfelder2022).
Figure 10 shows the radial-wavenumber dependence of the density-fluctuation power spectrum (blue lines) that would be sampled as the microwave beam propagates through the plasma. The product of the filter function
![]() $|F_{x\mu }|^2$
and the density-fluctuation power is shown in red. These quantities are plotted as a function of the turbulent
$|F_{x\mu }|^2$
and the density-fluctuation power is shown in red. These quantities are plotted as a function of the turbulent
![]() $k_x$
normalised by
$k_x$
normalised by
![]() $\rho _s$
using
$\rho _s$
using
![]() $k_x \rho _s = (k_x/K_0)(K_0\rho _s)$
. The solid lines correspond to
$k_x \rho _s = (k_x/K_0)(K_0\rho _s)$
. The solid lines correspond to
![]() $k_x$
scattered after the turning point (
$k_x$
scattered after the turning point (
![]() $k_x \gt 0$
in figure 9
b), while the dashed lines correspond to
$k_x \gt 0$
in figure 9
b), while the dashed lines correspond to
![]() $k_x$
scattered before the turning point (
$k_x$
scattered before the turning point (
![]() $k_x\lt 0$
in figure 9
b). As expected, the filter function has an important effect on the DBS signal power for smaller incidence angles
$k_x\lt 0$
in figure 9
b). As expected, the filter function has an important effect on the DBS signal power for smaller incidence angles
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }$
, while it becomes unimportant for larger
$\alpha _0 = 10^{\circ }, 30^{\circ }$
, while it becomes unimportant for larger
![]() $\alpha _0$
, at which point, the spectral falloff of the density spectrum becomes the dominant effect determining the
$\alpha _0$
, at which point, the spectral falloff of the density spectrum becomes the dominant effect determining the
![]() $k_x$
selection in the DBS measurement. Note, for example, that the peaking of the filter function near the plasma exit for
$k_x$
selection in the DBS measurement. Note, for example, that the peaking of the filter function near the plasma exit for
![]() $\alpha _0=50^{\circ }$
becomes negligible because it occurs at large
$\alpha _0=50^{\circ }$
becomes negligible because it occurs at large
![]() $k_x$
. Importantly, figure 10 contains both information about the radial localisation of the DBS power (if plotted as a function of
$k_x$
. Importantly, figure 10 contains both information about the radial localisation of the DBS power (if plotted as a function of
![]() $\tau$
) as well as the
$\tau$
) as well as the
![]() $k_x$
-selectivity of the power spectrum in the DBS measurement (plotted as a function of
$k_x$
-selectivity of the power spectrum in the DBS measurement (plotted as a function of
![]() $k_x$
) through the combined effect of the filter function and the turbulent spectrum. We stress again that, in this discussion, we are neglecting the spatial dependence of the turbulence intensity and spectrum,
$k_x$
) through the combined effect of the filter function and the turbulent spectrum. We stress again that, in this discussion, we are neglecting the spatial dependence of the turbulence intensity and spectrum,
![]() $\langle |\delta \hat {n}|^2 \rangle _T$
, which is assumed not to vary along the path.
$\langle |\delta \hat {n}|^2 \rangle _T$
, which is assumed not to vary along the path.
Ultimately, one of the main purposes of DBS diagnostics as a turbulence measurement is to obtain the density-fluctuation power spectrum in the binormal wavenumber of the turbulence, known as
![]() $k_\perp$
in the DBS jargon. In the context of this manuscript,
$k_\perp$
in the DBS jargon. In the context of this manuscript,
![]() $k_\perp$
is
$k_\perp$
is
![]() $k_y$
. To understand the impact of the filter function in such a measurement, in figure 11(a), we plot the integrated filter function
$k_y$
. To understand the impact of the filter function in such a measurement, in figure 11(a), we plot the integrated filter function
![]() $|F_{x\mu }|^2$
over the relevant
$|F_{x\mu }|^2$
over the relevant
![]() $k_x$
which would be sampled as the beam propagates through the plasma as a function of the selected wavenumber
$k_x$
which would be sampled as the beam propagates through the plasma as a function of the selected wavenumber
![]() $k_{y} = 2K_0 \sin \alpha _0$
. Since
$k_{y} = 2K_0 \sin \alpha _0$
. Since
![]() $|F_{x\mu }|^2$
multiplies the density-fluctuation spectrum
$|F_{x\mu }|^2$
multiplies the density-fluctuation spectrum
![]() $\langle |\delta \hat {n}|^2 \rangle _T$
, a constant
$\langle |\delta \hat {n}|^2 \rangle _T$
, a constant
![]() $\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
as a function of
$\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
as a function of
![]() $k_{y}$
would suggest that the DBS measurement is able to reproduce the true shape of the density-fluctuation wavenumber power spectrum
$k_{y}$
would suggest that the DBS measurement is able to reproduce the true shape of the density-fluctuation wavenumber power spectrum
![]() $\int \text {d}k_x\rho _s \langle |\delta \hat {n}|^2(k_x, k_{y}) \rangle _T$
. Figure 11(a) shows that the
$\int \text {d}k_x\rho _s \langle |\delta \hat {n}|^2(k_x, k_{y}) \rangle _T$
. Figure 11(a) shows that the
![]() $k_{y}$
dependence of
$k_{y}$
dependence of
![]() $\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
varies by a factor
$\int \text {d}k_x\rho _s |F_{x\mu }|^2/|F_0|^2$
varies by a factor
![]() $\sim 3$
for
$\sim 3$
for
![]() $k_{y}\rho _s \sim 0.4{-}40$
(
$k_{y}\rho _s \sim 0.4{-}40$
(
![]() $\alpha _0 \sim 3^{\circ }{-}80^{\circ }$
). The red dots correspond to the values of the integral of the filter function for
$\alpha _0 \sim 3^{\circ }{-}80^{\circ }$
). The red dots correspond to the values of the integral of the filter function for
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
$\alpha _0 = 10^{\circ }, 30^{\circ }, 50^{\circ }$
and
![]() $80^{\circ }$
. For small
$80^{\circ }$
. For small
![]() $k_{y}$
(small
$k_{y}$
(small
![]() $\alpha _0$
), the filter function is a decreasing function of
$\alpha _0$
), the filter function is a decreasing function of
![]() $k_{y}$
. This is due to the fact that for small
$k_{y}$
. This is due to the fact that for small
![]() $\alpha _0$
, the beam width focuses and produces an overall enhancement upon integration over the sampled
$\alpha _0$
, the beam width focuses and produces an overall enhancement upon integration over the sampled
![]() $k_x$
. In fact,
$k_x$
. In fact,
![]() $W_Y \sim \alpha _0$
for small
$W_Y \sim \alpha _0$
for small
![]() $\alpha _0$
(Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025), that is,
$\alpha _0$
(Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025), that is,
![]() $|F_{x\mu }|^2 \sim 1/\alpha _0^2$
(
$|F_{x\mu }|^2 \sim 1/\alpha _0^2$
(
![]() $K_\mu \sim \alpha _0$
). Since beam tracing assumes
$K_\mu \sim \alpha _0$
). Since beam tracing assumes
![]() $W_Y \gg \lambda$
, the decrease of
$W_Y \gg \lambda$
, the decrease of
![]() $W_Y$
at small
$W_Y$
at small
![]() $\alpha _0$
means that, for small enough angles, beam tracing is bound to break down: the prediction of a signal enhancement for small angles might overestimate the true enhancement in reality, as discussed in detail by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The precise angles for which this might happen and corrections to the beam-tracing model for small angles will be the subject of future publications.
$\alpha _0$
means that, for small enough angles, beam tracing is bound to break down: the prediction of a signal enhancement for small angles might overestimate the true enhancement in reality, as discussed in detail by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The precise angles for which this might happen and corrections to the beam-tracing model for small angles will be the subject of future publications.
For
![]() $k_{y}\rho _s \approx 4{-}5$
(
$k_{y}\rho _s \approx 4{-}5$
(
![]() $\alpha _0 \approx 30^{\circ }$
), the integrated filter function plateaus before abruptly decreasing for
$\alpha _0 \approx 30^{\circ }$
), the integrated filter function plateaus before abruptly decreasing for
![]() $\alpha _0 \approx 50^{\circ }$
. A similar plateau behaviour is observed in detailed measurements of the scattered power in DIII-D, reported in a recent publication by Pratt et al. (Reference Pratt2023). In our case, this is due to the fact that for such large angles, beam focusing has started to take place close to the plasma exit (see figure 9
b). This eliminates the signal enhancement due to the beam focusing inside the plasma (the
$\alpha _0 \approx 50^{\circ }$
. A similar plateau behaviour is observed in detailed measurements of the scattered power in DIII-D, reported in a recent publication by Pratt et al. (Reference Pratt2023). In our case, this is due to the fact that for such large angles, beam focusing has started to take place close to the plasma exit (see figure 9
b). This eliminates the signal enhancement due to the beam focusing inside the plasma (the
![]() $k_x$
integration is only performed inside the plasma), therefore decreasing the value of the integrated filter function. For larger
$k_x$
integration is only performed inside the plasma), therefore decreasing the value of the integrated filter function. For larger
![]() $k_{y}$
(
$k_{y}$
(
![]() $\alpha _0 \gtrsim 60^{\circ }$
), the integrated filter increases. This last increase is due to the fact that the launch condition at the plasma edge starts to become important. For such large incidence angles, the beam is practically glancing and can be treated as a high-k backscattering system (Rhodes et al. Reference Rhodes, Peebles, Nguyen, VanZeeland, deGrassie, Doyle, Wang and Zeng2006; Hillesheim et al. Reference Hillesheim, Crocker, Peebles, Meyer, Meakins, Field, Dunai, Carr and Hawkes2015). Figure 11(a) shows that the range of sampled radial wavenumbers in the density-fluctuation spectrum can have an important effect on the measured DBS power spectrum.
$\alpha _0 \gtrsim 60^{\circ }$
), the integrated filter increases. This last increase is due to the fact that the launch condition at the plasma edge starts to become important. For such large incidence angles, the beam is practically glancing and can be treated as a high-k backscattering system (Rhodes et al. Reference Rhodes, Peebles, Nguyen, VanZeeland, deGrassie, Doyle, Wang and Zeng2006; Hillesheim et al. Reference Hillesheim, Crocker, Peebles, Meyer, Meakins, Field, Dunai, Carr and Hawkes2015). Figure 11(a) shows that the range of sampled radial wavenumbers in the density-fluctuation spectrum can have an important effect on the measured DBS power spectrum.
Figure 11(b) shows the turbulence binormal-wavenumber power spectrum
![]() $\langle |\delta \hat {n}|^2(k_x=0, k_y) \rangle _T$
(black) corresponding to
$\langle |\delta \hat {n}|^2(k_x=0, k_y) \rangle _T$
(black) corresponding to
![]() $k_x=0$
. This follows the traditional interpretation that dominant contributions to the DBS signal originate from the cutoff. The magenta line shows the
$k_x=0$
. This follows the traditional interpretation that dominant contributions to the DBS signal originate from the cutoff. The magenta line shows the
![]() $k_x$
-integrated wavenumber spectrum
$k_x$
-integrated wavenumber spectrum
![]() $\int \text {d}k_x\rho _s \langle |\delta \hat {n}|^2 (k_x, k_y)\rangle _T$
. This could be interpreted as a line-integrated measurement of the density-fluctuation spectrum. The DBS system can be interpreted as a line-integrated measurement for large angles
$\int \text {d}k_x\rho _s \langle |\delta \hat {n}|^2 (k_x, k_y)\rangle _T$
. This could be interpreted as a line-integrated measurement of the density-fluctuation spectrum. The DBS system can be interpreted as a line-integrated measurement for large angles
![]() $\alpha _0$
, since for large
$\alpha _0$
, since for large
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $|F_{x\mu }|^2$
varies slowly and is not strongly peaked (see figure 7
d). The extent to which it can be interpreted as a line integral rather than a localised measurement is quantified by the filter function
$|F_{x\mu }|^2$
varies slowly and is not strongly peaked (see figure 7
d). The extent to which it can be interpreted as a line integral rather than a localised measurement is quantified by the filter function
![]() $|F_{x\mu }|^2$
, which we discuss next.
$|F_{x\mu }|^2$
, which we discuss next.
The blue dots in figure 11(b) show expected synthetic scattered power spectrum in a DBS measurement, given by the quantity
![]() $\int \text {d} k_x\rho _s \left ( |F_{x\mu }|^2/|F_0|^2 \right ) \langle |\delta \hat {n}|^2 \rangle _T (k_x, k_{y})$
in this beam-tracing model (see (3.9)). For each incidence angle
$\int \text {d} k_x\rho _s \left ( |F_{x\mu }|^2/|F_0|^2 \right ) \langle |\delta \hat {n}|^2 \rangle _T (k_x, k_{y})$
in this beam-tracing model (see (3.9)). For each incidence angle
![]() $\alpha _0$
(each
$\alpha _0$
(each
![]() $k_{y}$
), the synthetic DBS scattered power includes the effect of the filter function and the radial wavenumber dependence of the density-fluctuation spectrum. As expected from the non-monotonic nature of
$k_{y}$
), the synthetic DBS scattered power includes the effect of the filter function and the radial wavenumber dependence of the density-fluctuation spectrum. As expected from the non-monotonic nature of
![]() $\int \text {d}k_x\rho _s |F_{x\mu }|^2 / |F_0|^2$
from figure 11(a), the synthetic scattered power does not reproduce the true density-fluctuation wavenumber spectrum for
$\int \text {d}k_x\rho _s |F_{x\mu }|^2 / |F_0|^2$
from figure 11(a), the synthetic scattered power does not reproduce the true density-fluctuation wavenumber spectrum for
![]() $k_x=0$
nor the
$k_x=0$
nor the
![]() $k_x$
-integrated spectrum. The peak in the density-fluctuation power spectrum (
$k_x$
-integrated spectrum. The peak in the density-fluctuation power spectrum (
![]() $k_y\rho _s \approx 6{-}8$
), which is the driving scale of the turbulence, cannot be identified in the synthetic power spectrum. The peak should be visible for
$k_y\rho _s \approx 6{-}8$
), which is the driving scale of the turbulence, cannot be identified in the synthetic power spectrum. The peak should be visible for
![]() $\alpha _0 \approx 30^{\circ }{-}40^{\circ }$
, where the beam model is expected to be quantitatively accurate (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The enhancement of the synthetic scattered power with respect to the true turbulence spectrum for low
$\alpha _0 \approx 30^{\circ }{-}40^{\circ }$
, where the beam model is expected to be quantitatively accurate (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The enhancement of the synthetic scattered power with respect to the true turbulence spectrum for low
![]() $k_{y}$
(small incidence angles
$k_{y}$
(small incidence angles
![]() $\alpha _0 \lesssim 20^{\circ }$
) is due to the enhancement of the signal by beam focusing. For larger
$\alpha _0 \lesssim 20^{\circ }$
) is due to the enhancement of the signal by beam focusing. For larger
![]() $k_{y}\rho _s \gtrsim 10$
(
$k_{y}\rho _s \gtrsim 10$
(
![]() $\alpha _0 \gtrsim 40^{\circ }$
), the synthetic spectrum exhibits a power-law spectral decay
$\alpha _0 \gtrsim 40^{\circ }$
), the synthetic spectrum exhibits a power-law spectral decay
![]() $\propto k_{y}^{-3.05}$
, which is different from that of the true turbulent spectrum for
$\propto k_{y}^{-3.05}$
, which is different from that of the true turbulent spectrum for
![]() $k_x=0$
(
$k_x=0$
(
![]() $\propto k_{y}^{-4.16}$
). The spectral decay is shown to quantitatively agree with the
$\propto k_{y}^{-4.16}$
). The spectral decay is shown to quantitatively agree with the
![]() $k_x$
-integrated spectrum, for which
$k_x$
-integrated spectrum, for which
![]() $\propto k_{y}^{-2.84}$
. This suggests that DBS scattered power measurements could accurately capture the spectral exponent of the
$\propto k_{y}^{-2.84}$
. This suggests that DBS scattered power measurements could accurately capture the spectral exponent of the
![]() $k_x$
-integrated spectrum, in contrast to the traditional belief that DBS measurements only select the
$k_x$
-integrated spectrum, in contrast to the traditional belief that DBS measurements only select the
![]() $k_x=0$
component (Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012; Holland et al. Reference Holland2012). For this particular NSTX-inspired case, the DBS scattered power measurements can quantitatively reproduce the true spectral exponent of the
$k_x=0$
component (Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012; Holland et al. Reference Holland2012). For this particular NSTX-inspired case, the DBS scattered power measurements can quantitatively reproduce the true spectral exponent of the
![]() $k_x$
-integrated, density-fluctuation power spectrum.
$k_x$
-integrated, density-fluctuation power spectrum.
5. Conclusions and discussion
In this manuscript, we have discussed the phenomenon of beam focusing in the vicinity of a turning point. This phenomenon is not new and was already observed in numerical simulations for the 2-D linear-layer problem (Poli et al. Reference Poli, Pereverzev and Peeters1999, Reference Poli, Pereverzev, Peeters and Bornatici2001
Reference Poli, Pereverzev, Peeters and Bornaticic
; Yu. A. Kravtsov and Berczynski P., Reference Kravtsov and Berczynski2007), analytical calculations (Maj et al. Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010), as well as in numerical simulations in realistic tokamak geometry (Conway et al. Reference Conway, Troester, Schirmer, Angioni, Holzhauer, Jenko, Merz, Poli, Scott and Suttrop2007, Reference Conway, Lechte and Fochi2015, Reference Conway, Lechte, Poli and Maj2019). These results were confirmed in this work by numerical simulations using the Scotty code for an NBI-heated L-mode plasma in the JET tokamak. The analytic solution derived from a 2-D linear-layer problem adjusted to fit the experimental conditions of JET discharge 97 080 showed encouraging agreement with the Scotty simulations for realistic 3-D tokamak geometry. This motivated us to study the phenomenon of beam focusing in the linear-layer problem. We have characterised the beam focusing in terms of the initial incident angle
![]() $\alpha _0$
, initial width
$\alpha _0$
, initial width
![]() $W_0$
and initial radius of curvature
$W_0$
and initial radius of curvature
![]() $R_{Y0}$
. In particular, we have seen that beam focusing tends to be enhanced for decreasing angles, independently of
$R_{Y0}$
. In particular, we have seen that beam focusing tends to be enhanced for decreasing angles, independently of
![]() $R_{Y0}$
. For small enough
$R_{Y0}$
. For small enough
![]() $\alpha _0$
, the beam-tracing approximation becomes quantitatively inaccurate near the turning point, as discussed by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). Beam focusing also exhibits a clear dependence on the initial width
$\alpha _0$
, the beam-tracing approximation becomes quantitatively inaccurate near the turning point, as discussed by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). Beam focusing also exhibits a clear dependence on the initial width
![]() $W_0$
: initial widths small with respect to
$W_0$
: initial widths small with respect to
![]() $(\lambda L)^{\frac {1}{2}}$
lead to pronounced initial expansion due to diffraction of the electromagnetic waves as captured by the beam-tracing equations. Following the initial beam expansion for small
$(\lambda L)^{\frac {1}{2}}$
lead to pronounced initial expansion due to diffraction of the electromagnetic waves as captured by the beam-tracing equations. Following the initial beam expansion for small
![]() $W_0$
, the beam exhibits focusing in the vicinity of the turning point. For initial widths large with respect to
$W_0$
, the beam exhibits focusing in the vicinity of the turning point. For initial widths large with respect to
![]() $(\lambda L)^{\frac {1}{2}}$
, the initial expansion can completely disappear to yield only an initial contraction towards a maximum focusing location in the vicinity of the turning point. The value and location of the beam focusing is shown to depend on the initial conditions
$(\lambda L)^{\frac {1}{2}}$
, the initial expansion can completely disappear to yield only an initial contraction towards a maximum focusing location in the vicinity of the turning point. The value and location of the beam focusing is shown to depend on the initial conditions
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $W_0$
and
$W_0$
and
![]() $R_{Y0}$
.
$R_{Y0}$
.
We have used the analytical beam-tracing solution and applied it to the beam-tracing model for DBS (Hall-Chen et al., Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). We have found an analytic expression for the filter function
![]() $|F_{x\mu }|^2/ |F_0|^2 = K_0W_0/K_\mu W_{Y\mu }$
that characterises the scattering intensity along the beam path through the plasma, and we have studied it as a function of the beam initial conditions. This shows that
$|F_{x\mu }|^2/ |F_0|^2 = K_0W_0/K_\mu W_{Y\mu }$
that characterises the scattering intensity along the beam path through the plasma, and we have studied it as a function of the beam initial conditions. This shows that
![]() $W_{Y}$
is a critical parameter affecting the DBS scattering intensity along the path. We apply the lessons learned from our beam focusing formula to study the DBS filter function
$W_{Y}$
is a critical parameter affecting the DBS scattering intensity along the path. We apply the lessons learned from our beam focusing formula to study the DBS filter function
![]() $|F_{x\mu }|^2$
. When the beam focuses most (
$|F_{x\mu }|^2$
. When the beam focuses most (
![]() $W_{Y}$
is minimal), the filter function is enhanced. This means that DBS is most sensitive to enhanced contributions from the vicinity of the focusing point, and as a consequence, it is most sensitive for small angles
$W_{Y}$
is minimal), the filter function is enhanced. This means that DBS is most sensitive to enhanced contributions from the vicinity of the focusing point, and as a consequence, it is most sensitive for small angles
![]() $\alpha _0$
for which the focusing is large.
$\alpha _0$
for which the focusing is large.
The filter function
![]() $|F_{xy,\mu }|^2$
in terms of
$|F_{xy,\mu }|^2$
in terms of
![]() $k_x$
and
$k_x$
and
![]() $k_y$
in Cartesian coordinates opens the door to implementing synthetic diagnostics for DBS perfomed previously (White et al. Reference White2008; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Leerink et al. Reference Leerink, Bulanin, Gusakov, Heikkinen, Janhunen, Kiviniemi, Korpilo, Nora and Ogando2010; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012; Holland et al. Reference Holland2012; Leerink et al. Reference Leerink2012; Gusakov et al. Reference Gusakov2013; Krutkin et al., Reference Krutkin2019
Reference Krutkina
; Pratt et al. Reference Pratt2023; Patel et al. Reference Patel2024). In the
$k_y$
in Cartesian coordinates opens the door to implementing synthetic diagnostics for DBS perfomed previously (White et al. Reference White2008; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Leerink et al. Reference Leerink, Bulanin, Gusakov, Heikkinen, Janhunen, Kiviniemi, Korpilo, Nora and Ogando2010; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012; Holland et al. Reference Holland2012; Leerink et al. Reference Leerink2012; Gusakov et al. Reference Gusakov2013; Krutkin et al., Reference Krutkin2019
Reference Krutkina
; Pratt et al. Reference Pratt2023; Patel et al. Reference Patel2024). In the
![]() $k_x$
direction, we recover formulae reported by Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) when applied to the case of the auto-correlation (power) spectrum. In previous work, Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) argued that a forward-scattering contribution to the DBS amplitude is responsible for the signal enhancement observed for decreasing incidence angle
$k_x$
direction, we recover formulae reported by Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) when applied to the case of the auto-correlation (power) spectrum. In previous work, Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) argued that a forward-scattering contribution to the DBS amplitude is responsible for the signal enhancement observed for decreasing incidence angle
![]() $\alpha _0$
, in DBS as well as in radial correlation Doppler reflectometry. The calculations by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) were based on the full-wave analytic solution to the Helmholtz equation, including the Airy-function behaviour near the turning point that is absent in our present description. Our work demonstrates that the enhancement of the DBS scattered power for decreasing incidence angles observed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) can be completely explained via beam tracing, without the need of capturing the Airy behaviour in the vicinity of the turning point. We show that the underlying principle behind the enhancement of the DBS power is the beam focusing near the turning point and not forward scattering (in the form described by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). The formulae from § 3 recover the
$\alpha _0$
, in DBS as well as in radial correlation Doppler reflectometry. The calculations by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) were based on the full-wave analytic solution to the Helmholtz equation, including the Airy-function behaviour near the turning point that is absent in our present description. Our work demonstrates that the enhancement of the DBS scattered power for decreasing incidence angles observed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) can be completely explained via beam tracing, without the need of capturing the Airy behaviour in the vicinity of the turning point. We show that the underlying principle behind the enhancement of the DBS power is the beam focusing near the turning point and not forward scattering (in the form described by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). The formulae from § 3 recover the
![]() $k_y$
-resolution, or diagnostic wavenumber resolution
$k_y$
-resolution, or diagnostic wavenumber resolution
![]() $\Delta k_y$
, that was already reported in previous work (Lin et al. Reference Lin, Nazikian, Irby and Marmar2001; Hirsch et al. Reference Hirsch, Holzhauer, Baldzuhn and Kurzan2001; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012). We find that
$\Delta k_y$
, that was already reported in previous work (Lin et al. Reference Lin, Nazikian, Irby and Marmar2001; Hirsch et al. Reference Hirsch, Holzhauer, Baldzuhn and Kurzan2001; Hillesheim et al. Reference Hillesheim, Holland, Schmitz, Kubota, Rhodes and Carter2012). We find that
![]() $\Delta k_y$
is dependent on the initial conditions
$\Delta k_y$
is dependent on the initial conditions
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $W_0$
and
$W_0$
and
![]() $R_{Y0}$
and on
$R_{Y0}$
and on
![]() $L$
, and is constant along the path.
$L$
, and is constant along the path.
In addition to discussing the effect of the filter function
![]() $|F_{x\mu }|^2$
on the total DBS scattered power measurement, we have studied the effect of the turbulent wavenumber spectrum on the measured total scattered power. We have used a realistic representation of the turbulence spectrum based on gyrokinetic simulations, as done by Ruiz et al. (Reference Ruiz2022). We show the combined effect of the
$|F_{x\mu }|^2$
on the total DBS scattered power measurement, we have studied the effect of the turbulent wavenumber spectrum on the measured total scattered power. We have used a realistic representation of the turbulence spectrum based on gyrokinetic simulations, as done by Ruiz et al. (Reference Ruiz2022). We show the combined effect of the
![]() $k_x$
dependence of the filter function and the
$k_x$
dependence of the filter function and the
![]() $k_x$
dependence of the turbulence spectrum. In an NSTX-inspired example, the filter function is shown to have a most dominant effect for small angles
$k_x$
dependence of the turbulence spectrum. In an NSTX-inspired example, the filter function is shown to have a most dominant effect for small angles
![]() $\alpha _0 = 10^{\circ }, 30^{\circ }$
since for these specific conditions, DBS is sensitive to low-to-intermediate
$\alpha _0 = 10^{\circ }, 30^{\circ }$
since for these specific conditions, DBS is sensitive to low-to-intermediate
![]() $k_y$
and the spectrum is large. For larger angles, the filter function selects larger
$k_y$
and the spectrum is large. For larger angles, the filter function selects larger
![]() $k_{y} = - 2 K_0 \sin \alpha _0$
. In the specific condition analysed,
$k_{y} = - 2 K_0 \sin \alpha _0$
. In the specific condition analysed,
![]() $\alpha _0 \gt 50^{\circ }$
corresponded to wavenumbers
$\alpha _0 \gt 50^{\circ }$
corresponded to wavenumbers
![]() $k_{y}$
with small turbulent power in the spectrum. In those conditions, the filter function was shown to have little effect on the measurement and the dominant contributions to the scattered power could directly be assessed from the intrinsic turbulent spectrum itself. We also show that the filter function integrated over
$k_{y}$
with small turbulent power in the spectrum. In those conditions, the filter function was shown to have little effect on the measurement and the dominant contributions to the scattered power could directly be assessed from the intrinsic turbulent spectrum itself. We also show that the filter function integrated over
![]() $k_x$
is far from being constant and is strongly dependent on the
$k_x$
is far from being constant and is strongly dependent on the
![]() $k_{y}$
selected. The integrated filter function can be affected by the beam focusing inside or outside the plasma and the launch condition. This shows that one expects the total scattered power to depend on the incident angle of beam injection in the plasma,
$k_{y}$
selected. The integrated filter function can be affected by the beam focusing inside or outside the plasma and the launch condition. This shows that one expects the total scattered power to depend on the incident angle of beam injection in the plasma,
![]() $\alpha _0$
. For the particular NSTX turbulent spectrum studied in this manuscript, we show that the measured DBS scattered power spectrum could not recover the peak in the true density-fluctuation spectrum. The power-law decay exponent of the synthetic DBS spectrum can reproduce the
$\alpha _0$
. For the particular NSTX turbulent spectrum studied in this manuscript, we show that the measured DBS scattered power spectrum could not recover the peak in the true density-fluctuation spectrum. The power-law decay exponent of the synthetic DBS spectrum can reproduce the
![]() $k_x$
-integrated turbulence spectrum, but not the spectrum for
$k_x$
-integrated turbulence spectrum, but not the spectrum for
![]() $k_x=0$
.
$k_x=0$
.
This work helps characterise and interpret the total scattered power measured by DBS. Little attention has been paid to the spectral frequency power spectrum and specific experimental analysis techniques that are usually employed to study it. For example, of particular importance is the dependence of the Doppler-shifted DBS frequency spectrum on the diagnostic wavenumber resolution, as well as the effect of the
![]() $k_x = 0$
component (which is directly related to the beam focusing). The impact on the measured frequency spectrum remains an open question, but could be easily tackled using the reduced filter function developed in this work. This will require further analysis of the model and comparisons to experiments, which could be the subject of future publications.
$k_x = 0$
component (which is directly related to the beam focusing). The impact on the measured frequency spectrum remains an open question, but could be easily tackled using the reduced filter function developed in this work. This will require further analysis of the model and comparisons to experiments, which could be the subject of future publications.
To our knowledge, the beam focusing discussed in this manuscript has never been experimentally observed and future experiments should seek to experimentally confirm it. One option could be to set up scattering experiments from plasma fluctuations which exhibit a density gradient (not necessarily in magnetic confinement devices). Arranging different viewing channels that are sensitive to different parts of the beam trajectory along the path and assuming that the intensity of the plasma fluctuations is similar between the different regions in the plasma that each channel is sensitive to, one should expect enhanced scattering contributions from channels that are aimed at regions where the beam is focused, since the beam intensity is enhanced.
Lastly, the model presented here has limitations for small enough incident angles
![]() $\alpha _0$
, that is, for close to normal incidence beams. One can show that the filter function
$\alpha _0$
, that is, for close to normal incidence beams. One can show that the filter function
![]() $|F_{x\mu }|^2 \propto 1/\alpha _0^2$
for small angles. That explains the highly peaked behaviour of the filter function in figures 5(a) and 7(a) near the focusing region. This behaviour has its origin in the beam-tracing solution for the electric field, for which one can show that
$|F_{x\mu }|^2 \propto 1/\alpha _0^2$
for small angles. That explains the highly peaked behaviour of the filter function in figures 5(a) and 7(a) near the focusing region. This behaviour has its origin in the beam-tracing solution for the electric field, for which one can show that
![]() $E_b \propto 1/\alpha _0$
for small angles (Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025). This was studied by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). However, as pointed out in Maj’s work, the validity of the beam-tracing approximation is questionable for small enough incident angles. The beam-tracing solution for
$E_b \propto 1/\alpha _0$
for small angles (Belrhali et al. Reference Belrhali, Ruiz Ruiz, Parra and Hall-Chen2025). This was studied by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). However, as pointed out in Maj’s work, the validity of the beam-tracing approximation is questionable for small enough incident angles. The beam-tracing solution for
![]() $E_b$
might be overpredicting the electric-field enhancement due to focusing. In the exact solution for the electric field, one expects Airy behaviour to become important through interference between the incident and returning beams in the vicinity of the turning point, especially in conditions in which the beam width
$E_b$
might be overpredicting the electric-field enhancement due to focusing. In the exact solution for the electric field, one expects Airy behaviour to become important through interference between the incident and returning beams in the vicinity of the turning point, especially in conditions in which the beam width
![]() $W_Y$
approaches the Airy length
$W_Y$
approaches the Airy length
![]() $l_{Ai} = (L/K_0^2)^{\frac {1}{3}}$
. This behaviour is absent in the beam-tracing model, which expands the Airy behaviour asymptotically far from the turning point. Although the beam-tracing solution might be overpredicting the electric-field enhancement in the vicinity of the focusing region, we are confident that the phenomenon of beam focusing is physical, as confirmed by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010) and by our recent work. Future work will seek to employ more sophisticated models than beam tracing that capture Airy behaviour (as done in recent publications, such as Lopez, Kur & Strozzi Reference Lopez, Kur and Strozzi2023) to quantify how accurate the total integrated power enhancement predicted by beam tracing is for small incidence angles.
$l_{Ai} = (L/K_0^2)^{\frac {1}{3}}$
. This behaviour is absent in the beam-tracing model, which expands the Airy behaviour asymptotically far from the turning point. Although the beam-tracing solution might be overpredicting the electric-field enhancement in the vicinity of the focusing region, we are confident that the phenomenon of beam focusing is physical, as confirmed by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010) and by our recent work. Future work will seek to employ more sophisticated models than beam tracing that capture Airy behaviour (as done in recent publications, such as Lopez, Kur & Strozzi Reference Lopez, Kur and Strozzi2023) to quantify how accurate the total integrated power enhancement predicted by beam tracing is for small incidence angles.
Acknowledgements
The authors acknowledge insightful discussions with T. Rhodes.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Engineering and Physical Sciences Research Council (J.R.R., grant numbers EP/R034737/1, EP/W026341/1); the A*STAR Green Seed Fund (V.H.H.C., grant number C231718014) and a Young Individual Research Grant (V.H.H.C., grant number M23M7c0127); the U.S. Department of Energy (F.I.P., contract number DE-AC02-09CH11466). The United States Government retains a non-exclusive, paid-up, irrevocable, world-wide licence to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Analytic beam-tracing solution for the linear-layer problem.
We solve the beam-tracing equations in a 2-D slab for the O-mode with a constant density gradient (
![]() $\omega _{pe}^2(x) = \Omega ^2 x/L$
, where
$\omega _{pe}^2(x) = \Omega ^2 x/L$
, where
![]() $x$
is our Cartesian coordinate in figure 1) and launch frequency
$x$
is our Cartesian coordinate in figure 1) and launch frequency
![]() $\Omega$
. We will make use of the dispersion relation
$\Omega$
. We will make use of the dispersion relation
![]() $H=0$
, which takes the form
$H=0$
, which takes the form
![]() $H = {K^2}/{K_0^2} - 1 + {\omega _{pe}^2}/{\Omega ^2} = 0$
for the O-mode. The general beam-tracing evolution equation for
$H = {K^2}/{K_0^2} - 1 + {\omega _{pe}^2}/{\Omega ^2} = 0$
for the O-mode. The general beam-tracing evolution equation for
![]() $\boldsymbol{\unicode{x1D6F9}}$
is calculated along the central ray path and reads (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
)
$\boldsymbol{\unicode{x1D6F9}}$
is calculated along the central ray path and reads (Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
)
The analytic solution to the Gaussian beam-tracing equations was already obtained by Pereverzev (Reference Pereverzev1998) and Poli et al. (Reference Poli, Pereverzev and Peeters1999) for the 2-D linear-layer problem and normal incidence (
![]() $\alpha _0 = 0$
). The solution for the oblique incidence angle was obtained by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The beam-tracing equation (A.1) in the linear-layer problem reduces to
$\alpha _0 = 0$
). The solution for the oblique incidence angle was obtained by Maj et al. (Reference Maj, Pereverzev and Poli2009, Reference Maj, Balakin and Poli2010). The beam-tracing equation (A.1) in the linear-layer problem reduces to
![]() ${\text {d} \boldsymbol{\unicode{x1D6F9}}}/{ \text {d} \tau } = -({2}/{K_0^2}) \boldsymbol{\unicode{x1D6F9}}^2$
since we have
${\text {d} \boldsymbol{\unicode{x1D6F9}}}/{ \text {d} \tau } = -({2}/{K_0^2}) \boldsymbol{\unicode{x1D6F9}}^2$
since we have
![]() $\nabla \nabla H = 0, \nabla _K \nabla H = \nabla \nabla _K H= 0$
and
$\nabla \nabla H = 0, \nabla _K \nabla H = \nabla \nabla _K H= 0$
and
![]() $\nabla _K \nabla _K H = ({2}/{K_0^2}) \mathbf {I}$
, where
$\nabla _K \nabla _K H = ({2}/{K_0^2}) \mathbf {I}$
, where
![]() $\mathbf {I}$
is the identity matrix. Normalising
$\mathbf {I}$
is the identity matrix. Normalising
![]() $\boldsymbol{\unicode{x1D6F9}}$
by
$\boldsymbol{\unicode{x1D6F9}}$
by
![]() $K_0/L$
and
$K_0/L$
and
![]() $\tau$
by
$\tau$
by
![]() $K_0L$
, the corresponding solution for
$K_0L$
, the corresponding solution for
![]() $\boldsymbol{\unicode{x1D6F9}}^{\prime} = \boldsymbol{\unicode{x1D6F9}} ({L}/{K_0})$
is
$\boldsymbol{\unicode{x1D6F9}}^{\prime} = \boldsymbol{\unicode{x1D6F9}} ({L}/{K_0})$
is
The matrix
![]() $\boldsymbol{\unicode{x1D6F9}}^{\prime}$
must also satisfy the constraint
$\boldsymbol{\unicode{x1D6F9}}^{\prime}$
must also satisfy the constraint
At
![]() $\tau = 0$
, (A.3) gives
$\tau = 0$
, (A.3) gives
 \begin{align} \boldsymbol{\unicode{x1D6F9}}^{\prime}(0) = \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{xx0}^{\prime} & \Psi _{xy0}^{\prime} & \Psi _{xz0}^{\prime} \\ \Psi _{xy0}^{\prime} & \Psi _{yy0}^{\prime} & \Psi _{yz0}^{\prime} \\ \Psi _{xz0}^{\prime} & \Psi _{yz0}^{\prime} & \Psi _{zz0}^{\prime} \\ \end{array} \right) = \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{yy0}^{\prime} \tan ^2\alpha _0 - \frac {1}{2\cos \alpha _0} & - \Psi _{yy0}^{\prime} \tan \alpha _0 & 0 \\ - \Psi _{yy0}^{\prime} \tan \alpha _0 & \Psi _{yy0}^{\prime} & 0 \\ 0 & 0 & \Psi _{zz0}^{\prime} \\ \end{array} \right), \end{align}
\begin{align} \boldsymbol{\unicode{x1D6F9}}^{\prime}(0) = \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{xx0}^{\prime} & \Psi _{xy0}^{\prime} & \Psi _{xz0}^{\prime} \\ \Psi _{xy0}^{\prime} & \Psi _{yy0}^{\prime} & \Psi _{yz0}^{\prime} \\ \Psi _{xz0}^{\prime} & \Psi _{yz0}^{\prime} & \Psi _{zz0}^{\prime} \\ \end{array} \right) = \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{yy0}^{\prime} \tan ^2\alpha _0 - \frac {1}{2\cos \alpha _0} & - \Psi _{yy0}^{\prime} \tan \alpha _0 & 0 \\ - \Psi _{yy0}^{\prime} \tan \alpha _0 & \Psi _{yy0}^{\prime} & 0 \\ 0 & 0 & \Psi _{zz0}^{\prime} \\ \end{array} \right), \end{align}
where the zeros along the third row and column are a particular choice of initial condition. With this choice, one only needs
![]() $\Psi _{yy0}^{\prime}$
and
$\Psi _{yy0}^{\prime}$
and
![]() $\alpha _0$
to specify the initial conditions for the beam in the 2-D linear-layer problem.
$\alpha _0$
to specify the initial conditions for the beam in the 2-D linear-layer problem.
The beam-tracing equations are more easily solved in the lab frame
![]() $\{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(figure 1), but to interpret the results, it is useful to use the beam frame. Noting that
$\{ {\hat{\mathbf{x}}}, {\hat{\mathbf{y}}}, {\hat{\mathbf{z}}} \}$
(figure 1), but to interpret the results, it is useful to use the beam frame. Noting that
![]() $\mathbf {r} = \mathbf {q} + Y \hat {\mathbf {Y}} + X \hat {\mathbf {X}}$
, we find that
$\mathbf {r} = \mathbf {q} + Y \hat {\mathbf {Y}} + X \hat {\mathbf {X}}$
, we find that
![]() $\left (\mathbf {r} - \mathbf {q}(\tau ) \right ) \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \left (\mathbf {r} - \mathbf {q}(\tau ) \right ) = \Psi _{YY} Y^2 + 2\Psi _{XY} XY + \Psi _{XX} X^2$
, where
$\left (\mathbf {r} - \mathbf {q}(\tau ) \right ) \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \left (\mathbf {r} - \mathbf {q}(\tau ) \right ) = \Psi _{YY} Y^2 + 2\Psi _{XY} XY + \Psi _{XX} X^2$
, where
![]() $\Psi _{YY} = \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {Y}}$
,
$\Psi _{YY} = \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {Y}}$
,
![]() $\Psi _{XY} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {Y}}$
and
$\Psi _{XY} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {Y}}$
and
![]() $\Psi _{XX} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {X}}$
. The other components of
$\Psi _{XX} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {X}}$
. The other components of
![]() $\boldsymbol{\unicode{x1D6F9}}$
are defined by
$\boldsymbol{\unicode{x1D6F9}}$
are defined by
![]() $\Psi _{Yg} = \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
,
$\Psi _{Yg} = \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
,
![]() $\Psi _{Xg} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
and
$\Psi _{Xg} = \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
and
![]() $\Psi _{gg} = \hat {\mathbf {g}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
. They are determined from (A.3) and given by
$\Psi _{gg} = \hat {\mathbf {g}} \cdot \boldsymbol{\unicode{x1D6F9}} \cdot \hat {\mathbf {g}}$
. They are determined from (A.3) and given by
 \begin{align} \begin{aligned} & \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{Y}}} \big ) \frac {L}{K_0} , \\ & \hat {\mathbf {g}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{g}}} \big ) \frac {L}{K_0} , \\ & \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{X}}} \big ) \frac {L}{K_0} = 0 . \end{aligned} \end{align}
\begin{align} \begin{aligned} & \hat {\mathbf {Y}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{Y}}} \big ) \frac {L}{K_0} , \\ & \hat {\mathbf {g}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{g}}} \big ) \frac {L}{K_0} , \\ & \hat {\mathbf {X}} \cdot \boldsymbol{\unicode{x1D6F9}}^{\prime} \cdot \hat {\mathbf {g}} &&= - \frac {1}{g} \big ( \nabla H \cdot {\hat{\mathbf{X}}} \big ) \frac {L}{K_0} = 0 . \end{aligned} \end{align}
Evaluating (A.5) at
![]() $\tau =0$
, we have
$\tau =0$
, we have
 \begin{align} \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{YY0}^{\prime} & \Psi _{Yg0}^{\prime} & \Psi _{YX0}^{\prime} \\ \Psi _{Yg0}^{\prime} & \Psi _{gg0}^{\prime} & \Psi _{Xg0}^{\prime} \\ \Psi _{YX0}^{\prime} & \Psi _{Xg0}^{\prime} & \Psi _{XX0}^{\prime} \\ \end{array} \right) = \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{YY0}^{\prime} & - \frac {1}{2} \sin \alpha _0 & 0 \\ - \frac {1}{2} \sin \alpha _0 & - \frac {1}{2} \cos \alpha _0 & 0 \\ 0 & 0 & \Psi _{zz0}^{\prime} \\ \end{array} \right), \end{align}
\begin{align} \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{YY0}^{\prime} & \Psi _{Yg0}^{\prime} & \Psi _{YX0}^{\prime} \\ \Psi _{Yg0}^{\prime} & \Psi _{gg0}^{\prime} & \Psi _{Xg0}^{\prime} \\ \Psi _{YX0}^{\prime} & \Psi _{Xg0}^{\prime} & \Psi _{XX0}^{\prime} \\ \end{array} \right) = \left(\begin{array}{c@{\quad}c@{\quad}c} \Psi _{YY0}^{\prime} & - \frac {1}{2} \sin \alpha _0 & 0 \\ - \frac {1}{2} \sin \alpha _0 & - \frac {1}{2} \cos \alpha _0 & 0 \\ 0 & 0 & \Psi _{zz0}^{\prime} \\ \end{array} \right), \end{align}
where
![]() $\Psi _{YY0}^{\prime}$
is the beam-frame initial condition. In (A.6), the initial condition
$\Psi _{YY0}^{\prime}$
is the beam-frame initial condition. In (A.6), the initial condition
![]() $\Psi ^{\prime}_{YX0} = 0$
is a choice that is consistent with (A.4), and the component
$\Psi ^{\prime}_{YX0} = 0$
is a choice that is consistent with (A.4), and the component
![]() $\Psi _{YY0}^{\prime}$
in (A.6) is related to
$\Psi _{YY0}^{\prime}$
in (A.6) is related to
![]() $\Psi _{yy0}^{\prime}$
in (A.4). We proceed to discuss how.
$\Psi _{yy0}^{\prime}$
in (A.4). We proceed to discuss how.
According to our discussion above, the matrix
![]() $\boldsymbol{\unicode{x1D6F9}}$
is given by
$\boldsymbol{\unicode{x1D6F9}}$
is given by
 \begin{align} \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{YY} & \Psi _{Yg} & \Psi _{YX} \\ \Psi _{Yg} & \Psi _{gg} & \Psi _{Xg} \\ \Psi _{YX} & \Psi _{Xg} & \Psi _{XX} \\ \end{array} \right) = \mathbf {R}^{\text {T}}_{\alpha }(\tau ) \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{xx} & \Psi _{xy} & \Psi _{xz} \\ \Psi _{xy} & \Psi _{yy} & \Psi _{yz} \\ \Psi _{xz} & \Psi _{yz} & \Psi _{zz} \\ \end{array}\right) \mathbf {R}_{\alpha }(\tau ), \end{align}
\begin{align} \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{YY} & \Psi _{Yg} & \Psi _{YX} \\ \Psi _{Yg} & \Psi _{gg} & \Psi _{Xg} \\ \Psi _{YX} & \Psi _{Xg} & \Psi _{XX} \\ \end{array} \right) = \mathbf {R}^{\text {T}}_{\alpha }(\tau ) \left(\begin{array}{l@{\quad}l@{\quad}l} \Psi _{xx} & \Psi _{xy} & \Psi _{xz} \\ \Psi _{xy} & \Psi _{yy} & \Psi _{yz} \\ \Psi _{xz} & \Psi _{yz} & \Psi _{zz} \\ \end{array}\right) \mathbf {R}_{\alpha }(\tau ), \end{align}
where
 \begin{align} \mathbf {R_\alpha }(\tau ) = \left(\begin{array}{c@{\quad}c@{\quad}c} \sin \alpha (\tau ) & \cos \alpha (\tau ) & 0 \\ -\cos \alpha (\tau ) & \sin \alpha (\tau ) & 0\\ 0 & 0 & 1 \\ \end{array} \right) . \end{align}
\begin{align} \mathbf {R_\alpha }(\tau ) = \left(\begin{array}{c@{\quad}c@{\quad}c} \sin \alpha (\tau ) & \cos \alpha (\tau ) & 0 \\ -\cos \alpha (\tau ) & \sin \alpha (\tau ) & 0\\ 0 & 0 & 1 \\ \end{array} \right) . \end{align}
Equations (A.7) and (A.8) show that the components of
![]() $\boldsymbol{\unicode{x1D6F9}}$
in the lab frame are related to those in the beam frame by a change of basis that corresponds to a simple rotation of angle
$\boldsymbol{\unicode{x1D6F9}}$
in the lab frame are related to those in the beam frame by a change of basis that corresponds to a simple rotation of angle
![]() $\pi /2 - \alpha$
along
$\pi /2 - \alpha$
along
![]() ${\hat{\mathbf{z}}} = {\hat{\mathbf{X}}}$
(figure 1). Note that
${\hat{\mathbf{z}}} = {\hat{\mathbf{X}}}$
(figure 1). Note that
![]() $\Psi _{YX} = 0$
implies
$\Psi _{YX} = 0$
implies
![]() $\Psi _{xz} = \Psi _{yz} = 0$
, which gives an easy interpretation to our choice of initial conditions in (A.4): the cross-section of the beam is not tilted in the
$\Psi _{xz} = \Psi _{yz} = 0$
, which gives an easy interpretation to our choice of initial conditions in (A.4): the cross-section of the beam is not tilted in the
![]() $\{ \hat {\mathbf {X}}, \hat {\mathbf {Y}} \}$
plane.
$\{ \hat {\mathbf {X}}, \hat {\mathbf {Y}} \}$
plane.
The evolution of the angle
![]() $\alpha$
along the path can be easily computed from the trajectory of the central ray (see (2.9)). It is given by
$\alpha$
along the path can be easily computed from the trajectory of the central ray (see (2.9)). It is given by
 \begin{align} \begin{aligned} & \tan \alpha = \frac {\tan \alpha _0}{1-\tau ^{\prime} / \cos \alpha _0} = \sin \alpha _0 \frac {K_0}{K_x} , \\ & \sin \alpha = \frac {\sin \alpha _0}{(1 - 2\tau ^{\prime}\cos \alpha _0 + \tau ^{\prime2})^{1/2}} = \sin \alpha _0 \frac {K_0}{K} , \\ & \cos \alpha = \frac {\cos \alpha _0 - \tau ^{\prime} }{(1-2\tau ^{\prime}\cos \alpha _0+\tau ^{\prime2})^{1/2}} = \frac {K_x}{K} . \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \tan \alpha = \frac {\tan \alpha _0}{1-\tau ^{\prime} / \cos \alpha _0} = \sin \alpha _0 \frac {K_0}{K_x} , \\ & \sin \alpha = \frac {\sin \alpha _0}{(1 - 2\tau ^{\prime}\cos \alpha _0 + \tau ^{\prime2})^{1/2}} = \sin \alpha _0 \frac {K_0}{K} , \\ & \cos \alpha = \frac {\cos \alpha _0 - \tau ^{\prime} }{(1-2\tau ^{\prime}\cos \alpha _0+\tau ^{\prime2})^{1/2}} = \frac {K_x}{K} . \\ \end{aligned} \end{align}
Using (A.7) and (A.8), one can relate the beam-frame initial condition
![]() $\Psi _{YY0} = {K_0}/{R_{Y0}} + i {2}/{W_{0}^2}$
to the lab-frame initial condition
$\Psi _{YY0} = {K_0}/{R_{Y0}} + i {2}/{W_{0}^2}$
to the lab-frame initial condition
![]() $\Psi _{yy0}^{\prime}$
, yielding
$\Psi _{yy0}^{\prime}$
, yielding
![]() $\Psi _{YY0}^{\prime} = - {\sin ^2\alpha _0}/{(2\cos \alpha _0)} + {\Psi _{yy0}^{\prime}}/{\cos ^2\alpha _0}$
. The change of basis in (A.7) also gives the following relations between all the beam-frame and lab-frame components:
$\Psi _{YY0}^{\prime} = - {\sin ^2\alpha _0}/{(2\cos \alpha _0)} + {\Psi _{yy0}^{\prime}}/{\cos ^2\alpha _0}$
. The change of basis in (A.7) also gives the following relations between all the beam-frame and lab-frame components:
 \begin{align} \begin{aligned} & \Psi _{YY}(\tau ^{\prime}) = \Psi _{xx} \sin ^2\alpha - 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\cos ^2\alpha , \\ & \Psi _{Yg}(\tau ^{\prime}) = \big (\Psi _{xx}-\Psi _{yy} \big )\sin \alpha \cos \alpha + \Psi _{x y} \big (\sin ^2\alpha - \cos ^2\alpha \big ) , \\ & \Psi _{gg}(\tau ^{\prime}) = \Psi _{xx}\cos ^2\alpha + 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\sin ^2\alpha , \\ & \Psi _{XX}(\tau ^{\prime}) = \Psi _{zz} . \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{YY}(\tau ^{\prime}) = \Psi _{xx} \sin ^2\alpha - 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\cos ^2\alpha , \\ & \Psi _{Yg}(\tau ^{\prime}) = \big (\Psi _{xx}-\Psi _{yy} \big )\sin \alpha \cos \alpha + \Psi _{x y} \big (\sin ^2\alpha - \cos ^2\alpha \big ) , \\ & \Psi _{gg}(\tau ^{\prime}) = \Psi _{xx}\cos ^2\alpha + 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\sin ^2\alpha , \\ & \Psi _{XX}(\tau ^{\prime}) = \Psi _{zz} . \\ \end{aligned} \end{align}
We now provide the lab-frame solution, derived from (A.2),
 \begin{align} \begin{aligned} & \Psi _{xx}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{xx0} + 2 \Delta _0 \tau ^{\prime} }{ D(\tau ^{\prime}) } , \\ & \Psi _{x y}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{x y 0} }{ D(\tau ^{\prime}) } , \\ & \Psi _{yy}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{yy0} + 2 \Delta _0 \tau ^{\prime} }{ D(\tau ^{\prime}) } . \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{xx}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{xx0} + 2 \Delta _0 \tau ^{\prime} }{ D(\tau ^{\prime}) } , \\ & \Psi _{x y}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{x y 0} }{ D(\tau ^{\prime}) } , \\ & \Psi _{yy}^{\prime}(\tau ^{\prime}) &&= \frac { \Psi ^{\prime}_{yy0} + 2 \Delta _0 \tau ^{\prime} }{ D(\tau ^{\prime}) } . \\ \end{aligned} \end{align}
Here, the denominator
![]() $D(\tau ^{\prime})$
can be readily expressed in terms of the lab-frame
$D(\tau ^{\prime})$
can be readily expressed in terms of the lab-frame
![]() ${\hat{\mathbf{x}}}$
component of the central ray
${\hat{\mathbf{x}}}$
component of the central ray
![]() $\mathbf {K}$
,
$\mathbf {K}$
,
![]() $K_x$
, yielding
$K_x$
, yielding
 \begin{align} \begin{aligned} & D(\tau ^{\prime}) &&= 1 + 2\tau ^{\prime} \textrm {Tr}_0 + 4\Delta _0\tau ^{\prime2} \\ & &&= \frac {1}{\cos \alpha _0} \frac {K_x}{K_0} + 2 \frac {\Psi _{yy0}^{\prime}}{\cos \alpha _0} \bigg ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \bigg ) , \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & D(\tau ^{\prime}) &&= 1 + 2\tau ^{\prime} \textrm {Tr}_0 + 4\Delta _0\tau ^{\prime2} \\ & &&= \frac {1}{\cos \alpha _0} \frac {K_x}{K_0} + 2 \frac {\Psi _{yy0}^{\prime}}{\cos \alpha _0} \bigg ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \bigg ) , \\ \end{aligned} \end{align}
with
 \begin{align} \begin{aligned} & \Delta _0 &&= (\Psi _{yy}^{\prime}\Psi _{xx}^{\prime} - \Psi _{x y}^{\prime2})_0 = (\Psi _{YY}^{\prime}\Psi _{gg}^{\prime} - \Psi _{Yg}^{\prime2})_0 = - \frac {\Psi _{yy0}^{\prime}}{2\cos \alpha _0} , \\ & \textrm {Tr}_0 &&= (\Psi _{yy}^{\prime} + \Psi _{xx}^{\prime})_0 = (\Psi _{gg}^{\prime} + \Psi _{YY}^{\prime})_0 = - \frac {1}{2\cos \alpha _0} + \frac { \Psi _{yy0}^{\prime} }{\cos ^2\alpha _0} , \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Delta _0 &&= (\Psi _{yy}^{\prime}\Psi _{xx}^{\prime} - \Psi _{x y}^{\prime2})_0 = (\Psi _{YY}^{\prime}\Psi _{gg}^{\prime} - \Psi _{Yg}^{\prime2})_0 = - \frac {\Psi _{yy0}^{\prime}}{2\cos \alpha _0} , \\ & \textrm {Tr}_0 &&= (\Psi _{yy}^{\prime} + \Psi _{xx}^{\prime})_0 = (\Psi _{gg}^{\prime} + \Psi _{YY}^{\prime})_0 = - \frac {1}{2\cos \alpha _0} + \frac { \Psi _{yy0}^{\prime} }{\cos ^2\alpha _0} , \\ \end{aligned} \end{align}
where we used
![]() $\tau ^{\prime} = \cos \alpha _0 - K_x/K_0$
. It is convenient to express (A.11) in terms of
$\tau ^{\prime} = \cos \alpha _0 - K_x/K_0$
. It is convenient to express (A.11) in terms of
![]() $K_x$
and the initial conditions
$K_x$
and the initial conditions
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $\Psi _{yy0}^{\prime}$
and
$\Psi _{yy0}^{\prime}$
and
![]() $K_0$
. We have
$K_0$
. We have
 \begin{align} \begin{aligned} & \Psi _{xx}^{\prime} && = \sin ^2\alpha _0 \frac {K_0^2}{K_x^2} \Psi _{yy}^{\prime} - \frac {1}{2} \frac {K_0}{K_x} , \\ & \Psi _{x y}^{\prime} && = - \sin \alpha _0 \frac {K_0}{K_x} \Psi ^{\prime}_{yy} , \\ & \Psi _{yy}^{\prime} &&= \frac { \Psi ^{\prime}_{yy0} \frac {K_x}{K_0} }{ \cos \alpha _0 D(K_x) } . \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{xx}^{\prime} && = \sin ^2\alpha _0 \frac {K_0^2}{K_x^2} \Psi _{yy}^{\prime} - \frac {1}{2} \frac {K_0}{K_x} , \\ & \Psi _{x y}^{\prime} && = - \sin \alpha _0 \frac {K_0}{K_x} \Psi ^{\prime}_{yy} , \\ & \Psi _{yy}^{\prime} &&= \frac { \Psi ^{\prime}_{yy0} \frac {K_x}{K_0} }{ \cos \alpha _0 D(K_x) } . \\ \end{aligned} \end{align}
The denominator
![]() $D$
in (A.14) is a function of
$D$
in (A.14) is a function of
![]() $K_x$
and is evaluated using the second line of (A.12).
$K_x$
and is evaluated using the second line of (A.12).
Using the evolution of the angle
![]() $\alpha$
along the path in (A.9), and
$\alpha$
along the path in (A.9), and
![]() $\Psi _{YY}(\tau ^{\prime}) = \Psi _{xx} \sin ^2\alpha - 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\cos ^2\alpha$
(see (A.10)), we arrive at the final solution for
$\Psi _{YY}(\tau ^{\prime}) = \Psi _{xx} \sin ^2\alpha - 2 \Psi _{x y}\sin \alpha \cos \alpha + \Psi _{yy}\cos ^2\alpha$
(see (A.10)), we arrive at the final solution for
![]() $\Psi _{YY}^{\prime}$
given in (2.10). Equation (2.10) contains the beam-focusing phenomenon for the 2-D linear-layer problem through
$\Psi _{YY}^{\prime}$
given in (2.10). Equation (2.10) contains the beam-focusing phenomenon for the 2-D linear-layer problem through
![]() $W_Y = \big ( 2/\Im [\Psi _{YY}]\big )^{\frac {1}{2}}$
. Expressing
$W_Y = \big ( 2/\Im [\Psi _{YY}]\big )^{\frac {1}{2}}$
. Expressing
![]() $\Psi _{YY}$
as a function of the central ray
$\Psi _{YY}$
as a function of the central ray
![]() $K_x$
is convenient, since it readily allows us to express
$K_x$
is convenient, since it readily allows us to express
![]() $W_Y$
as a function of the turbulent scattered
$W_Y$
as a function of the turbulent scattered
![]() $k_x$
, as done in this manuscript. We simply substitute
$k_x$
, as done in this manuscript. We simply substitute
![]() $k_x = - 2 K_x$
(Bragg condition).
$k_x = - 2 K_x$
(Bragg condition).
At this point, it is worth relating the beam-tracing solution to previous work. Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) employ particular initial conditions for the beam-tracing equations. Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) perform their calculations in the lab frame, setting the initial conditions to
 \begin{align} \begin{aligned} & \Psi _{yy0}^{\prime} && \equiv i \gamma , \\ & \Psi _{xx0}^{\prime} && = i \gamma \tan ^2\alpha _0 - \frac {1}{2\cos \alpha _0} , \qquad \\ & \Psi _{xy0}^{\prime} && = - {i \gamma \tan \alpha _0} , \\ \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{yy0}^{\prime} && \equiv i \gamma , \\ & \Psi _{xx0}^{\prime} && = i \gamma \tan ^2\alpha _0 - \frac {1}{2\cos \alpha _0} , \qquad \\ & \Psi _{xy0}^{\prime} && = - {i \gamma \tan \alpha _0} , \\ \end{aligned} \end{align}
where
![]() $\gamma = L/(K_0 \rho ^2)$
is purely real. Equations (A.15) are very particular initial conditions since they define a purely imaginary
$\gamma = L/(K_0 \rho ^2)$
is purely real. Equations (A.15) are very particular initial conditions since they define a purely imaginary
![]() $\Psi _{yy0}$
in the lab frame, but not in the beam frame. This means that this initial condition does not correspond to the beam waist at launch, but has a specific initial value for the radius of curvature in the beam frame. Using the relation between
$\Psi _{yy0}$
in the lab frame, but not in the beam frame. This means that this initial condition does not correspond to the beam waist at launch, but has a specific initial value for the radius of curvature in the beam frame. Using the relation between
![]() $\Psi _{YY0}$
and
$\Psi _{YY0}$
and
![]() $\Psi _{yy0}$
in (A.10), we have
$\Psi _{yy0}$
in (A.10), we have
![]() $ R_{Y0}/L = - {2 \cos \alpha _0}/{\sin ^2\alpha _0}$
,
$ R_{Y0}/L = - {2 \cos \alpha _0}/{\sin ^2\alpha _0}$
,
![]() $W_{0} = \sqrt {2}\rho \cos \alpha _0$
. Note that we can recover expressions by Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) by setting
$W_{0} = \sqrt {2}\rho \cos \alpha _0$
. Note that we can recover expressions by Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) by setting
![]() $\Psi _{yy0}^{\prime} \rightarrow i \gamma$
. In the work of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017), (A.11), (A.12) and (A.13) show that
$\Psi _{yy0}^{\prime} \rightarrow i \gamma$
. In the work of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017), (A.11), (A.12) and (A.13) show that
![]() $\Psi _{yy}^{\prime}$
can be explicitly written as
$\Psi _{yy}^{\prime}$
can be explicitly written as
 \begin{align} \begin{aligned} & \Psi _{yy}^{\prime}(K_x) &&= \frac {2 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x} \sin ^2\alpha _0 - \frac {K_x}{K_0} \Big ) }{1 + 4 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x}\sin ^2\alpha _0 - \frac {K_x}{K_0} \Big )^2 } \\ & && + \frac {i \gamma }{ 1 + 4 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x} \sin ^2\alpha _0 - \frac {K_x}{K_0} \Big )^2 } . \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{yy}^{\prime}(K_x) &&= \frac {2 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x} \sin ^2\alpha _0 - \frac {K_x}{K_0} \Big ) }{1 + 4 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x}\sin ^2\alpha _0 - \frac {K_x}{K_0} \Big )^2 } \\ & && + \frac {i \gamma }{ 1 + 4 \gamma ^2 \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} + \frac {K_0}{K_x} \sin ^2\alpha _0 - \frac {K_x}{K_0} \Big )^2 } . \end{aligned} \end{align}
The particular initial conditions from Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) finally yield
 \begin{align} \begin{aligned} & \Psi _{YY}^{\prime}(K_x) &&= \frac { -\frac {1}{2} \sin ^2\alpha _0 + i \gamma \Big [ \frac {K_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac {K_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} \big(\cos ^2\alpha _0-\sin ^2\alpha _0 \big) \Big ] }{ \Big [ \sin ^2\alpha _0 + \frac {K_x^2}{K_0^2} \Big ] \Big [ \frac {K_x}{K_0} + 2 i \gamma \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0 }{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \Big ) \Big ] } . \end{aligned} \end{align}
\begin{align} \begin{aligned} & \Psi _{YY}^{\prime}(K_x) &&= \frac { -\frac {1}{2} \sin ^2\alpha _0 + i \gamma \Big [ \frac {K_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac {K_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} \big(\cos ^2\alpha _0-\sin ^2\alpha _0 \big) \Big ] }{ \Big [ \sin ^2\alpha _0 + \frac {K_x^2}{K_0^2} \Big ] \Big [ \frac {K_x}{K_0} + 2 i \gamma \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0 }{\cos \alpha _0} \frac {K_x}{K_0} + \sin ^2\alpha _0 - \frac {K_x^2}{K_0^2} \Big ) \Big ] } . \end{aligned} \end{align}
Using
![]() $W_Y$
computed from (A.17) and
$W_Y$
computed from (A.17) and
![]() $|F_{x\mu }|^2/|F_0|^2 = K_0W_0/K_\mu W_{Y\mu }$
recovers (14) and (15) from Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
$|F_{x\mu }|^2/|F_0|^2 = K_0W_0/K_\mu W_{Y\mu }$
recovers (14) and (15) from Gusakov et al. (Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
Appendix B. Details of the scattered power calculations
In this appendix, we provide details of the scattered-power calculations in the 2-D linear-layer problem from § 3. We follow a derivation analogous to that of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), but using Cartesian coordinates instead of beam-aligned coordinates. The position
![]() $(x,y)$
in Cartesian coordinates is related to the
$(x,y)$
in Cartesian coordinates is related to the
![]() $(\tau , Y)$
coordinates by
$(\tau , Y)$
coordinates by
![]() $x = x_c(\tau ) + Y \sin \alpha (\tau ), y = y_c(\tau ) - Y\cos \alpha (\tau )$
(see (3.2)), where
$x = x_c(\tau ) + Y \sin \alpha (\tau ), y = y_c(\tau ) - Y\cos \alpha (\tau )$
(see (3.2)), where
![]() $(x_c, y_c)$
are the coordinates along the central ray (figure 1), and
$(x_c, y_c)$
are the coordinates along the central ray (figure 1), and
![]() $\sin \alpha$
and
$\sin \alpha$
and
![]() $\cos \alpha$
are given by (A.9). The density fluctuations are expressed in terms of
$\cos \alpha$
are given by (A.9). The density fluctuations are expressed in terms of
![]() $(x,y)$
and the conjugate turbulent wavevector is expressed in its Cartesian components
$(x,y)$
and the conjugate turbulent wavevector is expressed in its Cartesian components
![]() $\mathbf {k}_\perp = k_x {\hat{\mathbf{x}}} + k_y {\hat{\mathbf{y}}}$
, that is, we have
$\mathbf {k}_\perp = k_x {\hat{\mathbf{x}}} + k_y {\hat{\mathbf{y}}}$
, that is, we have
![]() $\delta n(x,y,t) = \int {\text {d}k_x \text {d}k_y \ \delta \hat {n}(k_x, k_y) \exp ({i k_x x + i k_y y }})$
(see (3.1)). Starting from (100) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), the scattered amplitude can be written as
$\delta n(x,y,t) = \int {\text {d}k_x \text {d}k_y \ \delta \hat {n}(k_x, k_y) \exp ({i k_x x + i k_y y }})$
(see (3.1)). Starting from (100) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), the scattered amplitude can be written as
 \begin{align} {A}_r(t) = &\frac {i \Omega A_{ant} }{2\pi c} \int { \text {d}V \ \text {d}k_x \ \text {d}k_y} \ \Im [{\Psi }_{YY}]^{\frac {1}{2}} \Im [{\Psi }_{XX}]^{\frac {1}{2}} \frac {g_{ant}}{g} \exp (i2\phi _G) \frac {\delta \hat {n}}{n} \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ] \nonumber \\ & \times \exp \left [ i \left ( 2s + k_x \left ( x_c(\tau ) + Y \sin \alpha \right ) + k_y \left ( y_c(\tau ) - Y \cos \alpha \right )\right.\right. \nonumber \\ & \left.\left.+ X^2 \Psi _{XX} + Y^2 \Psi _{YY} \right ) \right ] , \end{align}
\begin{align} {A}_r(t) = &\frac {i \Omega A_{ant} }{2\pi c} \int { \text {d}V \ \text {d}k_x \ \text {d}k_y} \ \Im [{\Psi }_{YY}]^{\frac {1}{2}} \Im [{\Psi }_{XX}]^{\frac {1}{2}} \frac {g_{ant}}{g} \exp (i2\phi _G) \frac {\delta \hat {n}}{n} \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ] \nonumber \\ & \times \exp \left [ i \left ( 2s + k_x \left ( x_c(\tau ) + Y \sin \alpha \right ) + k_y \left ( y_c(\tau ) - Y \cos \alpha \right )\right.\right. \nonumber \\ & \left.\left.+ X^2 \Psi _{XX} + Y^2 \Psi _{YY} \right ) \right ] , \end{align}
where the differential volume element is
![]() $\text {d} V \approx g\text {d}\tau \ \text {d}X \ \text {d}Y$
(see (114) of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and
$\text {d} V \approx g\text {d}\tau \ \text {d}X \ \text {d}Y$
(see (114) of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and
![]() $\boldsymbol {\epsilon }_{eq}$
is the equilibrium part of the cold-plasma dielectric tensor (note the approximately equal sign, since
$\boldsymbol {\epsilon }_{eq}$
is the equilibrium part of the cold-plasma dielectric tensor (note the approximately equal sign, since
![]() $\text {d}V$
has corrections of order
$\text {d}V$
has corrections of order
![]() $\sim \lambda /W$
due to the fact that
$\sim \lambda /W$
due to the fact that
![]() $\hat {\mathbf {X}}$
and
$\hat {\mathbf {X}}$
and
![]() $\hat {\mathbf {Y}}$
depend on
$\hat {\mathbf {Y}}$
depend on
![]() $\tau$
). In (B.1), the integrals in
$\tau$
). In (B.1), the integrals in
![]() $X$
and
$X$
and
![]() $Y$
are integrals of a complex Gaussian and give
$Y$
are integrals of a complex Gaussian and give
 \begin{align} \begin{alignedat}{2} & {A}_r(t) = && \frac {- \Omega A_{ant} g_{ant}}{2 c} \int {\text {d}k_x \text {d}k_y \frac {\delta \hat {n}}{n} } \int {\text {d}\tau }\bigg [ \frac {\Im [{\Psi }_{YY}]}{ \Psi _{YY} } \bigg ]^{\frac {1}{2}} \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ] \\ & && \times \exp ({i2\phi _G}) \exp [{if(\tau )}] , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & {A}_r(t) = && \frac {- \Omega A_{ant} g_{ant}}{2 c} \int {\text {d}k_x \text {d}k_y \frac {\delta \hat {n}}{n} } \int {\text {d}\tau }\bigg [ \frac {\Im [{\Psi }_{YY}]}{ \Psi _{YY} } \bigg ]^{\frac {1}{2}} \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ] \\ & && \times \exp ({i2\phi _G}) \exp [{if(\tau )}] , \\ \end{alignedat} \end{align}
where we set
![]() $\Im [\Psi _{XX}]/\Psi _{XX} = 1$
(to be able to ignore the variation along the field line direction
$\Im [\Psi _{XX}]/\Psi _{XX} = 1$
(to be able to ignore the variation along the field line direction
![]() $X$
). Here,
$X$
). Here,
![]() $f(\tau )$
is
$f(\tau )$
is
where
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} = k_x \sin \alpha - k_y \cos \alpha$
from (3.5). The largest piece in
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} = k_x \sin \alpha - k_y \cos \alpha$
from (3.5). The largest piece in
![]() $f$
is given by
$f$
is given by
where
![]() $f_0 \sim L/\lambda$
. The last term in (B.3) is order
$f_0 \sim L/\lambda$
. The last term in (B.3) is order
![]() $\sim 1$
, since
$\sim 1$
, since
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
. Naively, this would suggest calculating the integral in
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
. Naively, this would suggest calculating the integral in
![]() $\tau$
from (B.2) via the method of stationary phase using
$\tau$
from (B.2) via the method of stationary phase using
![]() $\text {d} f_0/\text {d}\tau = 0$
. This results in a point of stationary phase
$\text {d} f_0/\text {d}\tau = 0$
. This results in a point of stationary phase
![]() $\tau _\mu \sim L/\lambda$
that is real, but yields an error of order
$\tau _\mu \sim L/\lambda$
that is real, but yields an error of order
![]() $\sim 1$
in the result, as we shall see. The reason for this is subtle. While the exponent
$\sim 1$
in the result, as we shall see. The reason for this is subtle. While the exponent
![]() $\exp [i f(\tau )]$
from the
$\exp [i f(\tau )]$
from the
![]() $\tau$
integral in (B.2) appears to be imaginary at first sight, it is not quite imaginary due to the term
$\tau$
integral in (B.2) appears to be imaginary at first sight, it is not quite imaginary due to the term
![]() $\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ]$
. Even though this term is order
$\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ]$
. Even though this term is order
![]() $\sim 1$
, it ends up giving rise to an order
$\sim 1$
, it ends up giving rise to an order
![]() $\sim 1$
error in the result. This is because, despite being order
$\sim 1$
error in the result. This is because, despite being order
![]() $\sim 1$
, its first and second derivatives are not.
$\sim 1$
, its first and second derivatives are not.
We start by calculating the
![]() $\tau$
integral in (B.2) using the traditional stationary phase from the largest part
$\tau$
integral in (B.2) using the traditional stationary phase from the largest part
![]() $\exp [i f_0]$
, while keeping the term
$\exp [i f_0]$
, while keeping the term
![]() $\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ] \sim 1$
constant. We call
$\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ] \sim 1$
constant. We call
![]() $\tau _\mu$
the solution to
$\tau _\mu$
the solution to
![]() $\text {d} f_0/\text {d}\tau \big |_\mu = 0$
, which defines a point along the trajectory of the central ray where, for a given
$\text {d} f_0/\text {d}\tau \big |_\mu = 0$
, which defines a point along the trajectory of the central ray where, for a given
![]() $\mathbf {k}_\perp$
, we have the resonant Bragg condition
$\mathbf {k}_\perp$
, we have the resonant Bragg condition
![]() $2K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu = 0$
. Now, consider a point situated at a distance
$2K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu = 0$
. Now, consider a point situated at a distance
![]() $\Delta \tau \sim W/\lambda \ll \tau _\mu$
from
$\Delta \tau \sim W/\lambda \ll \tau _\mu$
from
![]() $\tau _\mu$
. At that point, the phase
$\tau _\mu$
. At that point, the phase
![]() $f_0$
gives the following contribution:
$f_0$
gives the following contribution:
where
![]() $ (\text {d}^2f_0/\text {d}\tau ^2) \big |_\mu (\Delta \tau )^2/2 \sim 1$
. Next, we calculate the contributions from
$ (\text {d}^2f_0/\text {d}\tau ^2) \big |_\mu (\Delta \tau )^2/2 \sim 1$
. Next, we calculate the contributions from
![]() $\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ]$
at
$\exp [{-} i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} ]$
at
![]() $\tau _\mu + \Delta \tau$
. We find
$\tau _\mu + \Delta \tau$
. We find
 \begin{align} \begin{alignedat}{2} & - \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2}{4 \Psi _{YY} } \bigg |_{\tau _\mu + \Delta \tau } =&& - \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu )^2}{4 \Psi _{YY\mu } } - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu )}{2\Psi _{YY\mu }} \frac {\text {d}\alpha }{\text {d}\tau } \bigg |_\mu \Delta \tau \\ & && - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2}{2\Psi _{YY\mu }} \left ( \frac {\text {d}\alpha }{\text {d}\tau } \right )^2 \bigg |_\mu \frac { (\Delta \tau )^2}{2} + O \left ( \frac {\lambda }{W} \right ) , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & - \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2}{4 \Psi _{YY} } \bigg |_{\tau _\mu + \Delta \tau } =&& - \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu )^2}{4 \Psi _{YY\mu } } - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu )}{2\Psi _{YY\mu }} \frac {\text {d}\alpha }{\text {d}\tau } \bigg |_\mu \Delta \tau \\ & && - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2}{2\Psi _{YY\mu }} \left ( \frac {\text {d}\alpha }{\text {d}\tau } \right )^2 \bigg |_\mu \frac { (\Delta \tau )^2}{2} + O \left ( \frac {\lambda }{W} \right ) , \\ \end{alignedat} \end{align}
where we used the following relation between the unit vectors:
 \begin{align} \begin{alignedat}{2} & \frac {\text {d}\hat {\mathbf {g}}}{\text {d} \tau } = - \hat {\mathbf {Y}} \frac {\text {d}\alpha }{\text {d} \tau } , \\ & \frac {\text {d}\hat {\mathbf {Y}}}{\text {d} \tau } = \hat {\mathbf {g}} \frac {\text {d}\alpha }{\text {d} \tau } . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\text {d}\hat {\mathbf {g}}}{\text {d} \tau } = - \hat {\mathbf {Y}} \frac {\text {d}\alpha }{\text {d} \tau } , \\ & \frac {\text {d}\hat {\mathbf {Y}}}{\text {d} \tau } = \hat {\mathbf {g}} \frac {\text {d}\alpha }{\text {d} \tau } . \\ \end{alignedat} \end{align}
Equation (B.7) can be easily proven by taking the derivative of the unit vectors in (2.6). Using the fact that
![]() $ \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \sim 1/\lambda$
and
$ \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \sim 1/\lambda$
and
![]() $ \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
, we note that all terms in (B.6) are
$ \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
, we note that all terms in (B.6) are
![]() $\sim 1$
. This is contradictory, because the term
$\sim 1$
. This is contradictory, because the term
![]() $- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} |_{\tau _\mu + \Delta \tau }$
in (B.6) should be approximately
$- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} |_{\tau _\mu + \Delta \tau }$
in (B.6) should be approximately
![]() $- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} |_\mu$
for the method of stationary phase to work. The corrections to that term from small deviations
$- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY} |_\mu$
for the method of stationary phase to work. The corrections to that term from small deviations
![]() $\Delta \tau$
should have been
$\Delta \tau$
should have been
![]() $\sim \lambda /W$
or smaller. They are not smaller because, despite being
$\sim \lambda /W$
or smaller. They are not smaller because, despite being
![]() $\sim 1$
at
$\sim 1$
at
![]() $\tau = \tau _\mu$
, the term
$\tau = \tau _\mu$
, the term
![]() $-(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4\Psi _{YY}$
is not
$-(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4\Psi _{YY}$
is not
![]() $\sim 1$
for
$\sim 1$
for
![]() $\tau - \tau _\mu \sim W/\lambda$
. The fact that we find that the corrections to that term from a small deviation
$\tau - \tau _\mu \sim W/\lambda$
. The fact that we find that the corrections to that term from a small deviation
![]() $\Delta \tau$
to
$\Delta \tau$
to
![]() $\tau _\mu$
are important suggests that, in fact, the term
$\tau _\mu$
are important suggests that, in fact, the term
![]() $- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY}$
has to be taken into account in the stationary phase calculation, alongside
$- i (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}})^2/4 \Psi _{YY}$
has to be taken into account in the stationary phase calculation, alongside
![]() $f_0$
, despite the fact that it is, at first sight, order
$f_0$
, despite the fact that it is, at first sight, order
![]() $\sim 1$
for
$\sim 1$
for
![]() $\tau = \tau _\mu$
and
$\tau = \tau _\mu$
and
![]() $f_0 \sim L/\lambda$
. Having shown this, we proceed to calculate the dominant contribution to the
$f_0 \sim L/\lambda$
. Having shown this, we proceed to calculate the dominant contribution to the
![]() $\tau$
integral in (B.2) by a method related to the steepest descent (Bender & Orszag Reference Bender and Orszag1978), but not exactly the steepest descent method.
$\tau$
integral in (B.2) by a method related to the steepest descent (Bender & Orszag Reference Bender and Orszag1978), but not exactly the steepest descent method.
The
![]() $\tau$
integral in (B.2) is dominated by the region around
$\tau$
integral in (B.2) is dominated by the region around
![]() $\text {d} f / \text {d} \tau = 0$
, where
$\text {d} f / \text {d} \tau = 0$
, where
where the first three terms on the right-hand side are order
![]() $\sim 1$
, the fourth term is order
$\sim 1$
, the fourth term is order
![]() $\sim \lambda /W$
and the last term is
$\sim \lambda /W$
and the last term is
![]() $\sim \lambda /L$
. Note that directly setting
$\sim \lambda /L$
. Note that directly setting
![]() $ \text {d} f / \text {d} \tau = 0$
(steepest descent) will give a complex value for
$ \text {d} f / \text {d} \tau = 0$
(steepest descent) will give a complex value for
![]() ${\tau }_\mu$
. One option to calculate the exact steepest descent point is to solve
${\tau }_\mu$
. One option to calculate the exact steepest descent point is to solve
![]() ${ \text {d} f }/{ \text {d} \tau } = 0$
for
${ \text {d} f }/{ \text {d} \tau } = 0$
for
![]() $\tau$
in (B.8), as a function of
$\tau$
in (B.8), as a function of
![]() $k_x, k_y, K_0L, \alpha _0$
and
$k_x, k_y, K_0L, \alpha _0$
and
![]() $\Psi _{yy0}$
, by using the exact expression for
$\Psi _{yy0}$
, by using the exact expression for
![]() $\Psi _{YY}$
in (2.10), as well as (A.9). This leads to a high-order polynomial in
$\Psi _{YY}$
in (2.10), as well as (A.9). This leads to a high-order polynomial in
![]() $\tau$
that does not admit an analytic solution in the general case. Instead, here we choose to solve
$\tau$
that does not admit an analytic solution in the general case. Instead, here we choose to solve
![]() ${ \text {d} f }/{ \text {d} \tau } = 0$
perturbatively for
${ \text {d} f }/{ \text {d} \tau } = 0$
perturbatively for
![]() $\tau$
in (B.8). We will find that the
$\tau$
in (B.8). We will find that the
![]() $\tau$
that satisfies (B.8) can be written as
$\tau$
that satisfies (B.8) can be written as
![]() $\tau _\mu + \Delta \tau$
, where
$\tau _\mu + \Delta \tau$
, where
![]() $\tau _\mu$
is the real solution to
$\tau _\mu$
is the real solution to
![]() $\text {d}f_0 / \text {d}\tau = 0$
(using (B.5)). We will find that
$\text {d}f_0 / \text {d}\tau = 0$
(using (B.5)). We will find that
![]() $\Delta \tau$
is complex. This appears to pose a problem, since the functions
$\Delta \tau$
is complex. This appears to pose a problem, since the functions
![]() $s$
,
$s$
,
![]() $x_c$
,
$x_c$
,
![]() $y_c$
,
$y_c$
,
![]() $\hat {\mathbf {Y}}$
and
$\hat {\mathbf {Y}}$
and
![]() $\Psi _{YY}$
in
$\Psi _{YY}$
in
![]() $f$
are functions of a real
$f$
are functions of a real
![]() $\tau$
. This means that we have to analytically continue them to the complex plane. One can wonder how much one can extended these functions away from real
$\tau$
. This means that we have to analytically continue them to the complex plane. One can wonder how much one can extended these functions away from real
![]() $\tau$
. That turns out not to be very important because we are going to prove that one only needs to modify the path by a very small amount: the saddle point will only be a small distance
$\tau$
. That turns out not to be very important because we are going to prove that one only needs to modify the path by a very small amount: the saddle point will only be a small distance
![]() $\Delta \tau \sim (W/L) \tau _\mu$
away from the original real path. Since
$\Delta \tau \sim (W/L) \tau _\mu$
away from the original real path. Since
![]() $W/L$
is an asymptotically small number, the deviation from the original path into the complex plane will be sufficiently small that no pole, branch point or fundamental singularity will be crossed.
$W/L$
is an asymptotically small number, the deviation from the original path into the complex plane will be sufficiently small that no pole, branch point or fundamental singularity will be crossed.
Having established the validity of the analytic continuation into the complex plane by distances of order
![]() $W/L$
from the original path, we now calculate that distance
$W/L$
from the original path, we now calculate that distance
![]() $\Delta \tau$
and how it contributes to the
$\Delta \tau$
and how it contributes to the
![]() $\tau$
integral in (B.2). We note that (B.3) implies that
$\tau$
integral in (B.2). We note that (B.3) implies that
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
, and hence the term proportional to
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
, and hence the term proportional to
![]() $( \mathbf {k}_\perp \cdot \hat {\mathbf {g}} )( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} )$
in (B.8) is small in
$( \mathbf {k}_\perp \cdot \hat {\mathbf {g}} )( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} )$
in (B.8) is small in
![]() $\lambda /W$
. This motivates splitting the root into two pieces
$\lambda /W$
. This motivates splitting the root into two pieces
![]() ${\tau }_\mu + \Delta \tau$
, where
${\tau }_\mu + \Delta \tau$
, where
![]() $\tau _\mu$
is real and
$\tau _\mu$
is real and
![]() $\Delta \tau \sim ({\lambda }/{W}) {\tau }_\mu$
is complex, and expanding the Bragg condition order by order in
$\Delta \tau \sim ({\lambda }/{W}) {\tau }_\mu$
is complex, and expanding the Bragg condition order by order in
![]() $\lambda /W$
. We denote quantities evaluated at
$\lambda /W$
. We denote quantities evaluated at
![]() ${\tau }_\mu$
with the subscript
${\tau }_\mu$
with the subscript
![]() $\mu$
(e.g.
$\mu$
(e.g.
![]() $K({\tau }_\mu ) = {K}_\mu$
). At the lowest order, we have
$K({\tau }_\mu ) = {K}_\mu$
). At the lowest order, we have
where
![]() $f_0$
is given by (B.4). The zeroth-order Bragg condition in (B.9) can be explicitly written in terms of
$f_0$
is given by (B.4). The zeroth-order Bragg condition in (B.9) can be explicitly written in terms of
![]() ${K}_{x\mu }$
as follows:
${K}_{x\mu }$
as follows:
 \begin{align} \begin{alignedat}{2} & 2 \frac {{K}_{x\mu }^2}{K_0^2} + \frac {k_x}{K_0} \frac {{K}_{x\mu }}{K_0} + \sin \alpha _0 \bigg ( \frac {k_y}{K_0} + 2 \sin \alpha _0 \bigg ) = 0 , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & 2 \frac {{K}_{x\mu }^2}{K_0^2} + \frac {k_x}{K_0} \frac {{K}_{x\mu }}{K_0} + \sin \alpha _0 \bigg ( \frac {k_y}{K_0} + 2 \sin \alpha _0 \bigg ) = 0 , \\ \end{alignedat} \end{align}
where we used (2.9) and the expression
![]() ${g}_\mu = 2 {{K}_\mu }/K_0^2$
. Using the fact that
${g}_\mu = 2 {{K}_\mu }/K_0^2$
. Using the fact that
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
and employing (A.9) gives
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
and employing (A.9) gives
![]() $k_x \approx k_y/\tan {\alpha }_\mu$
and hence
$k_x \approx k_y/\tan {\alpha }_\mu$
and hence
Note that (B.10) exhibits two solutions for
![]() ${K}_{x\mu }$
. Following (B.11), we expand the two solutions for small
${K}_{x\mu }$
. Following (B.11), we expand the two solutions for small
![]() $k_y + 2 K_0 \sin \alpha _0$
. We find
$k_y + 2 K_0 \sin \alpha _0$
. We find
where only the second solution
![]() $\sim 1/\lambda$
is physically relevant. This shows that
$\sim 1/\lambda$
is physically relevant. This shows that
![]() ${K}_{x\mu } = - k_x/2 + O(1/W)$
. As we anticipated, the Bragg condition calculated to zeroth-order is not sufficient to calculate the terms that are order
${K}_{x\mu } = - k_x/2 + O(1/W)$
. As we anticipated, the Bragg condition calculated to zeroth-order is not sufficient to calculate the terms that are order
![]() $\sim 1$
in the phase or in the amplitude.
$\sim 1$
in the phase or in the amplitude.
Next, we use the fact that
![]() $ \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \sim 1/\lambda$
and
$ \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \sim 1/\lambda$
and
![]() $ \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
to find the Bragg condition to next order in
$ \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \sim 1/W$
to find the Bragg condition to next order in
![]() $\lambda /W$
. This is done by finding the solution to (B.9) at
$\lambda /W$
. This is done by finding the solution to (B.9) at
![]() $\tau _\mu + \Delta \tau$
, by setting
$\tau _\mu + \Delta \tau$
, by setting
 \begin{align} \begin{alignedat}{2} & \frac { \text {d} f }{ \text {d} \tau } \Big |_{{\tau }_\mu + \Delta \tau } = \left ( 2K g + k_x\frac {\text {d}x_c}{\text {d}\tau } + k_y\frac {\text {d}y_c}{\text {d}\tau } - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}} ) ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} ) }{2\Psi _{YY}} \frac {\text {d}\alpha }{\text {d}\tau } \right )_{{\tau }_\mu + \Delta \tau } = 0. \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac { \text {d} f }{ \text {d} \tau } \Big |_{{\tau }_\mu + \Delta \tau } = \left ( 2K g + k_x\frac {\text {d}x_c}{\text {d}\tau } + k_y\frac {\text {d}y_c}{\text {d}\tau } - \frac {( \mathbf {k}_\perp \cdot \hat {\mathbf {g}} ) ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} ) }{2\Psi _{YY}} \frac {\text {d}\alpha }{\text {d}\tau } \right )_{{\tau }_\mu + \Delta \tau } = 0. \\ \end{alignedat} \end{align}
Note that the last term in (B.8) was dropped, since it contributes an order smaller. Equation (B.13) determines the value of
![]() $\Delta \tau$
, which is given by
$\Delta \tau$
, which is given by
 \begin{align} \begin{alignedat}{2} & \Delta \tau \approx \frac {\frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu ) (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu ) }{2 {\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu }{2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2_\mu } , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \Delta \tau \approx \frac {\frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu ) (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu ) }{2 {\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu }{2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2_\mu } , \\ \end{alignedat} \end{align}
where we can easily verify that
![]() $\Delta \tau \sim W/\lambda$
as anticipated. Having calculated the value of
$\Delta \tau \sim W/\lambda$
as anticipated. Having calculated the value of
![]() ${\tau }_\mu$
and
${\tau }_\mu$
and
![]() $\Delta \tau$
that satisfy the Bragg condition order by order in (B.9), (B.13) and (B.14), next, we approximate
$\Delta \tau$
that satisfy the Bragg condition order by order in (B.9), (B.13) and (B.14), next, we approximate
![]() $f(\tau ) \approx f({\tau }_\mu + \Delta \tau ) + {\text {d}^2 f}/{ \text {d} \tau ^2} \big |_{{\tau }_\mu + \Delta \tau } (\tau - {\tau }_\mu - \Delta \tau )^2 / 2$
. We find
$f(\tau ) \approx f({\tau }_\mu + \Delta \tau ) + {\text {d}^2 f}/{ \text {d} \tau ^2} \big |_{{\tau }_\mu + \Delta \tau } (\tau - {\tau }_\mu - \Delta \tau )^2 / 2$
. We find
 \begin{align} \begin{alignedat}{2} & f({\tau }_\mu + \Delta \tau ) &&\approx f( {\tau }_\mu ) + \Delta \tau \frac {\text {d} f}{ \text {d} \tau } \Big |_{{\tau }_\mu } + \frac {1}{2} \Delta \tau ^2 \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{ {\tau }_\mu } \approx f_0( {\tau }_\mu ) - \frac {\frac {\text {d}{K}}{\text {d}\tau } \big |_\mu {g}_\mu \frac {\left (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu ^2 } , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & f({\tau }_\mu + \Delta \tau ) &&\approx f( {\tau }_\mu ) + \Delta \tau \frac {\text {d} f}{ \text {d} \tau } \Big |_{{\tau }_\mu } + \frac {1}{2} \Delta \tau ^2 \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{ {\tau }_\mu } \approx f_0( {\tau }_\mu ) - \frac {\frac {\text {d}{K}}{\text {d}\tau } \big |_\mu {g}_\mu \frac {\left (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu ^2 } , \\ \end{alignedat} \end{align}
where
![]() $f_0$
is given by (B.4) and the second derivative term in (B.15) is given by
$f_0$
is given by (B.4) and the second derivative term in (B.15) is given by
 \begin{align} \begin{alignedat}{2} & \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{ {\tau }_\mu + \Delta \tau } && \approx \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{{\tau }_\mu } = 2 \frac {\text {d} {K}}{\text {d}\tau }\Big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \bigg ( \frac {\text {d}\alpha }{\text {d}\tau } \bigg )^2_\mu . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{ {\tau }_\mu + \Delta \tau } && \approx \frac {\text {d}^2 f}{ \text {d} \tau ^2 } \Big |_{{\tau }_\mu } = 2 \frac {\text {d} {K}}{\text {d}\tau }\Big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \bigg ( \frac {\text {d}\alpha }{\text {d}\tau } \bigg )^2_\mu . \end{alignedat} \end{align}
Note that the phase in (B.15) contains terms
![]() $\sim 1$
that cannot be recovered by restricting the stationary phase calculation to zeroth-order, that is, by calculating
$\sim 1$
that cannot be recovered by restricting the stationary phase calculation to zeroth-order, that is, by calculating
![]() $\text {d}f_0/\text {d}\tau = 0$
and keeping the term
$\text {d}f_0/\text {d}\tau = 0$
and keeping the term
![]() $- ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} )^2/4\Psi _{YY}$
in (B.3) constant.
$- ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} )^2/4\Psi _{YY}$
in (B.3) constant.
We are now in a position to perform the steepest-descent integral in (B.2). We find the following expression for the scattered amplitude in Cartesian coordinates:
where the slowly varying function (filter)
![]() ${F}_{xy,\mu }(k_x, k_y)$
takes the form
${F}_{xy,\mu }(k_x, k_y)$
takes the form
 \begin{align} \begin{alignedat}{2} &F_{xy,\mu }(k_x, k_y) = &&- \frac {\Omega g_{ant}}{2c} \left [ \frac {\Im [{ {\Psi }}_{YY\mu }] }{ {\Psi }_{YY\mu }} \right ]^{\frac {1}{2}} \frac {\big [ {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big ]_{{\tau }_\mu }}{{n}_\mu } \exp ({i 2 {\phi }_{G\mu }}) \\ & && \times \left ( \frac {2 i\pi }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \Big ( \frac {\text {d}\alpha }{\text {d}\tau } \Big )^2_{{\tau }_\mu } } \right )^{\frac {1}{2}} \exp \left [ - i \frac {\frac {\text {d}{K}}{\text {d}\tau }\big |_\mu {g}_\mu \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu ^2 } \right ] . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} &F_{xy,\mu }(k_x, k_y) = &&- \frac {\Omega g_{ant}}{2c} \left [ \frac {\Im [{ {\Psi }}_{YY\mu }] }{ {\Psi }_{YY\mu }} \right ]^{\frac {1}{2}} \frac {\big [ {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big ]_{{\tau }_\mu }}{{n}_\mu } \exp ({i 2 {\phi }_{G\mu }}) \\ & && \times \left ( \frac {2 i\pi }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \Big ( \frac {\text {d}\alpha }{\text {d}\tau } \Big )^2_{{\tau }_\mu } } \right )^{\frac {1}{2}} \exp \left [ - i \frac {\frac {\text {d}{K}}{\text {d}\tau }\big |_\mu {g}_\mu \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{2 {\Psi }_{YY\mu }} }{ 2 \frac {\text {d} {K}}{\text {d}\tau }\big |_\mu {g}_\mu - \frac {2 {K}_\mu ^2}{{\Psi }_{YY\mu }} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )_\mu ^2 } \right ] . \end{alignedat} \end{align}
Next, we calculate the scattered power following the same procedure as Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). For this calculation, we need the turbulence correlation function
![]() $C$
, defined as the Fourier transform of the density-fluctuation wavenumber power spectrum in Cartesian
$C$
, defined as the Fourier transform of the density-fluctuation wavenumber power spectrum in Cartesian
![]() $(k_x, k_y)$
coordinates,
$(k_x, k_y)$
coordinates,
 \begin{align} \begin{alignedat}{2} & C(\mathbf {r}, t, \Delta \mathbf {r}, \Delta t) &&= \frac {\langle \delta n (\mathbf {r} + \Delta \mathbf {r}, t + \Delta t) \delta n (\mathbf {r}, t) \rangle _T}{ \langle \delta {n}^2 \rangle _T } \\ & &&= \int \text {d}k_x \text {d}k_y \ \hat {C}(\mathbf {r}, t, k_x, k_y, z=0, \Delta t) \exp [{i(k_x \Delta x + k_y \Delta y )}]. \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & C(\mathbf {r}, t, \Delta \mathbf {r}, \Delta t) &&= \frac {\langle \delta n (\mathbf {r} + \Delta \mathbf {r}, t + \Delta t) \delta n (\mathbf {r}, t) \rangle _T}{ \langle \delta {n}^2 \rangle _T } \\ & &&= \int \text {d}k_x \text {d}k_y \ \hat {C}(\mathbf {r}, t, k_x, k_y, z=0, \Delta t) \exp [{i(k_x \Delta x + k_y \Delta y )}]. \end{alignedat} \end{align}
Here,
![]() $\langle \delta {n}^2 \rangle _T$
is the root-mean-square value of the density-fluctuation power. The function
$\langle \delta {n}^2 \rangle _T$
is the root-mean-square value of the density-fluctuation power. The function
![]() $\hat {C}$
is given by
$\hat {C}$
is given by
 \begin{align} \begin{alignedat}{2} & \hat {C}(\mathbf {r}, t, k_x, k_y) =&& \frac {1}{\langle \delta n^2 \rangle _T} \int { \text {d}k_x^{\prime} \text {d}k_y^{\prime} \big \langle \delta \hat {n}(k_x, k_y) \delta \hat {n}^*(k_x^{\prime}, k_y^{\prime}) \big \rangle _T } \\ & && \times \exp [i(k_x-k_x^{\prime})x + i(k_y-k_y^{\prime})y]. \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \hat {C}(\mathbf {r}, t, k_x, k_y) =&& \frac {1}{\langle \delta n^2 \rangle _T} \int { \text {d}k_x^{\prime} \text {d}k_y^{\prime} \big \langle \delta \hat {n}(k_x, k_y) \delta \hat {n}^*(k_x^{\prime}, k_y^{\prime}) \big \rangle _T } \\ & && \times \exp [i(k_x-k_x^{\prime})x + i(k_y-k_y^{\prime})y]. \end{alignedat} \end{align}
We order
![]() $k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
. We use (B.20) for
$k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
. We use (B.20) for
![]() $\hat {C}$
to calculate the scattered power. We start by calculating the product
$\hat {C}$
to calculate the scattered power. We start by calculating the product
![]() $\langle |A_r|^2 \rangle _T$
, which is given by
$\langle |A_r|^2 \rangle _T$
, which is given by
 \begin{align} \begin{alignedat}{2} & \big \langle |{A}_r(t)|^2 \big \rangle _T = &&|A_{ant}|^2 \int \text {d}k_x \text {d}k_y \ F_{xy,\mu }(k_x, k_y) \exp \big [i f_0(\tau _\mu ) \big ] \\ & && \times \int \text {d}k_x^{\prime} \text {d}k_y^{\prime} \ F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \exp \big [{-}i f_0(\tau _{\mu ^{\prime}}) \big ] \\ & && \times \big \langle \delta \hat {n}(k_x, k_y) \delta \hat {n}^*(k_x^{\prime}, k_y^{\prime}) \big \rangle _T, \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \big \langle |{A}_r(t)|^2 \big \rangle _T = &&|A_{ant}|^2 \int \text {d}k_x \text {d}k_y \ F_{xy,\mu }(k_x, k_y) \exp \big [i f_0(\tau _\mu ) \big ] \\ & && \times \int \text {d}k_x^{\prime} \text {d}k_y^{\prime} \ F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \exp \big [{-}i f_0(\tau _{\mu ^{\prime}}) \big ] \\ & && \times \big \langle \delta \hat {n}(k_x, k_y) \delta \hat {n}^*(k_x^{\prime}, k_y^{\prime}) \big \rangle _T, \end{alignedat} \end{align}
where
![]() $\mu ^{\prime}$
is the scattering position corresponding to
$\mu ^{\prime}$
is the scattering position corresponding to
![]() $(k_x^{\prime}, k_y^{\prime})$
, different from
$(k_x^{\prime}, k_y^{\prime})$
, different from
![]() $(k_x, k_y)$
. Note that
$(k_x, k_y)$
. Note that
![]() $F_{xy,\mu }$
does not change significantly if
$F_{xy,\mu }$
does not change significantly if
![]() $k_x$
or
$k_x$
or
![]() $k_y$
change by a small amount of order
$k_y$
change by a small amount of order
![]() $\sim 1/L$
. This means that we can neglect the differences
$\sim 1/L$
. This means that we can neglect the differences
![]() $k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
between
$k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
between
![]() $F_{xy,\mu }(k_x, k_y)$
and
$F_{xy,\mu }(k_x, k_y)$
and
![]() $F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime})$
, so that
$F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime})$
, so that
![]() $F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \approx F_{xy,\mu }^*(k_x, k_y)$
. The last step to calculate
$F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \approx F_{xy,\mu }^*(k_x, k_y)$
. The last step to calculate
![]() $ \langle |{A}_r(t)|^2 \rangle _T$
is to compute the difference in the large phase
$ \langle |{A}_r(t)|^2 \rangle _T$
is to compute the difference in the large phase
![]() $f_0(\tau _\mu ) - f_0(\tau _{\mu ^{\prime}})$
. Since
$f_0(\tau _\mu ) - f_0(\tau _{\mu ^{\prime}})$
. Since
![]() $f_0 \sim L/\lambda$
, it is important to keep the differences
$f_0 \sim L/\lambda$
, it is important to keep the differences
![]() $k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
; these differences will provide an order unity contribution to the phase. Straightforward calculations lead to
$k_x - k_x^{\prime} \sim k_y - k_y^{\prime} \sim 1/L$
; these differences will provide an order unity contribution to the phase. Straightforward calculations lead to
where we used the Bragg condition (B.10) and the definition of
![]() $s = \int K \text {d}l$
in Cartesian coordinates (see (2.5)). Using (B.22) and
$s = \int K \text {d}l$
in Cartesian coordinates (see (2.5)). Using (B.22) and
![]() $F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \approx F_{xy,\mu }^*(k_x, k_y)$
, we can relate the expression for
$F_{xy,\mu ^{\prime}}^*(k_x^{\prime}, k_y^{\prime}) \approx F_{xy,\mu }^*(k_x, k_y)$
, we can relate the expression for
![]() $\langle |{A}_r(t)|^2 \rangle _T$
to the correlation function in (B.20). Defining
$\langle |{A}_r(t)|^2 \rangle _T$
to the correlation function in (B.20). Defining
![]() $p_r = \langle |{A}_r(t)|^2 \rangle _T$
, we find
$p_r = \langle |{A}_r(t)|^2 \rangle _T$
, we find
where
![]() ${\mathbf {r}}_{c\mu } = ({x}_{c\mu }, {y}_{c\mu }, z=0)$
. The correlation function is related to the 2-D wavenumber power spectrum via
${\mathbf {r}}_{c\mu } = ({x}_{c\mu }, {y}_{c\mu }, z=0)$
. The correlation function is related to the 2-D wavenumber power spectrum via
![]() $\langle |\delta \hat {n} (k_x, k_y)|^2 \rangle _T = \langle \delta {n}^2 \rangle _T \hat {C} (\mathbf {r}, t, k_x, k_y, z=0, \Delta t=0)$
. The Cartesian filter function
$\langle |\delta \hat {n} (k_x, k_y)|^2 \rangle _T = \langle \delta {n}^2 \rangle _T \hat {C} (\mathbf {r}, t, k_x, k_y, z=0, \Delta t=0)$
. The Cartesian filter function
![]() $|F_{xy,\mu }|^2$
in (B.23) can be calculated directly using (B.18) and is given by
$|F_{xy,\mu }|^2$
in (B.23) can be calculated directly using (B.18) and is given by
 \begin{align} \begin{alignedat}{3} & |F_{xy,\mu }|^2 && = && 2\pi \Big ( \frac {\Omega g_{ant}}{2c} \Big )^2 \frac { \big | {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big |^2_{{\tau }_\mu } }{ {n}_\mu ^2} \\ & && && \times \frac { \Im [{{\Psi }}_{YY}]_\mu }{| {\Psi }_{YY}|_\mu } \frac { \exp \Bigg [ - \frac { \big (2 \frac {\text {d}{K}}{\text {d}\tau } \big )_\mu ^2 {g}_\mu ^2 }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY}} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu ^2 } \frac {2 \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{\Delta {k}_{\mu 2}^2} \Bigg ]}{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{ {\Psi }_{YY} } \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu } , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{3} & |F_{xy,\mu }|^2 && = && 2\pi \Big ( \frac {\Omega g_{ant}}{2c} \Big )^2 \frac { \big | {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big |^2_{{\tau }_\mu } }{ {n}_\mu ^2} \\ & && && \times \frac { \Im [{{\Psi }}_{YY}]_\mu }{| {\Psi }_{YY}|_\mu } \frac { \exp \Bigg [ - \frac { \big (2 \frac {\text {d}{K}}{\text {d}\tau } \big )_\mu ^2 {g}_\mu ^2 }{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{{\Psi }_{YY}} \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu ^2 } \frac {2 \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{\Delta {k}_{\mu 2}^2} \Bigg ]}{ \big | 2 \frac {\text {d} {K}}{\text {d}\tau } {g} - \frac {2 {K}^2}{ {\Psi }_{YY} } \big ( \frac {\text {d}\alpha }{\text {d}\tau } \big )^2 \big |_\mu } , \end{alignedat} \end{align}
where
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} = k_x \sin {\alpha }_\mu - k_y\cos {\alpha }_\mu$
(see (3.5)), and we have introduced the wavenumber resolution
$\mathbf {k}_\perp \cdot \hat {\mathbf {Y}} = k_x \sin {\alpha }_\mu - k_y\cos {\alpha }_\mu$
(see (3.5)), and we have introduced the wavenumber resolution
![]() $\Delta {k}_{\mu 2} = 2 \big ( {-1}/{\Im [{1}/{{\Psi }_{YY\mu } } ]} \big )^{\frac {1}{2}} = 2 {| {\Psi }_{YY\mu }|}/{ \Im [{\Psi }_{YY\mu } ]^{\frac {1}{2}} } \sim 1/W$
as defined by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). Note that the polarisation piece for the O-mode can be written as
$\Delta {k}_{\mu 2} = 2 \big ( {-1}/{\Im [{1}/{{\Psi }_{YY\mu } } ]} \big )^{\frac {1}{2}} = 2 {| {\Psi }_{YY\mu }|}/{ \Im [{\Psi }_{YY\mu } ]^{\frac {1}{2}} } \sim 1/W$
as defined by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). Note that the polarisation piece for the O-mode can be written as
![]() ${ \big | {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big |^2 } = {\omega _{pe}^4}/{ \Omega ^4}$
.
${ \big | {\hat{\mathbf{e}}}^{*} \cdot (\boldsymbol {\epsilon }_{eq} - \mathbf {1} ) \cdot {\hat{\mathbf{e}}} \big |^2 } = {\omega _{pe}^4}/{ \Omega ^4}$
.
Equation (B.24) for
![]() $|F_{xy,\mu }|^2$
is (3.8) in the main text. We note that (B.23) does not exactly recover the expressions of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Equation (B.23) can be further simplified by using the Bragg condition and the analytic beam-tracing solution, which we describe next. We will recover (3.9) in the main text. This result is valid for general beam initial conditions. By using Gusakov’s initial conditions in (A.15), we will recover the expressions for the scattered power (auto-correlation) derived by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
$|F_{xy,\mu }|^2$
is (3.8) in the main text. We note that (B.23) does not exactly recover the expressions of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Equation (B.23) can be further simplified by using the Bragg condition and the analytic beam-tracing solution, which we describe next. We will recover (3.9) in the main text. This result is valid for general beam initial conditions. By using Gusakov’s initial conditions in (A.15), we will recover the expressions for the scattered power (auto-correlation) derived by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
We want to express
![]() $|F_{xy,\mu }|^2$
as a function of its variables
$|F_{xy,\mu }|^2$
as a function of its variables
![]() $k_x$
and
$k_x$
and
![]() $k_y$
. The function
$k_y$
. The function
![]() $|F_{xy,\mu }(k_x, k_y)|^2$
in (B.23) is a function of
$|F_{xy,\mu }(k_x, k_y)|^2$
in (B.23) is a function of
![]() $(k_x, k_y)$
through the Bragg condition relating
$(k_x, k_y)$
through the Bragg condition relating
![]() ${\tau }_{\mu }$
to
${\tau }_{\mu }$
to
![]() $k_x$
and
$k_x$
and
![]() $k_y$
(see (B.9)). We proceed to calculate the different terms in (B.23). Using the Bragg condition
$k_y$
(see (B.9)). We proceed to calculate the different terms in (B.23). Using the Bragg condition
![]() $k_x \approx -2 K_{x\mu }$
, the ray-tracing solution for the central ray and the analytic expression for
$k_x \approx -2 K_{x\mu }$
, the ray-tracing solution for the central ray and the analytic expression for
![]() $\Psi _{YY}$
(see (2.10)), we proceed to simplify the terms outside of the exponential in (B.23). Using the formulae
$\Psi _{YY}$
(see (2.10)), we proceed to simplify the terms outside of the exponential in (B.23). Using the formulae
and
 \begin{align} \begin{alignedat}{2} & \bigg ( \frac { \text {d}\alpha }{ \text {d}\tau } \bigg )_\mu &&= \frac {\sin \alpha _0}{K_0L} \frac {K_0^2 }{K_\mu ^2} , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \bigg ( \frac { \text {d}\alpha }{ \text {d}\tau } \bigg )_\mu &&= \frac {\sin \alpha _0}{K_0L} \frac {K_0^2 }{K_\mu ^2} , \\ \end{alignedat} \end{align}
we find
 \begin{align} \begin{alignedat}{2} & 2 \frac {\text {d} {K}}{\text {d}\tau }\Big |_\mu {g}_\mu - 2 \frac { {K}_\mu ^2}{ {\Psi }_{YY\mu } } \bigg ( \frac {\text {d}\alpha }{\text {d}\tau }\bigg )_\mu ^2 = \\ & - \frac {4 \Psi _{yy0}^{\prime}}{K_0L} \frac { {K}_\mu ^4 / K_0^4 }{ - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big ( \frac { {K}_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac { {K}_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} (\cos ^2\alpha _0 - \sin ^2\alpha _0) \Big ) } . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & 2 \frac {\text {d} {K}}{\text {d}\tau }\Big |_\mu {g}_\mu - 2 \frac { {K}_\mu ^2}{ {\Psi }_{YY\mu } } \bigg ( \frac {\text {d}\alpha }{\text {d}\tau }\bigg )_\mu ^2 = \\ & - \frac {4 \Psi _{yy0}^{\prime}}{K_0L} \frac { {K}_\mu ^4 / K_0^4 }{ - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big ( \frac { {K}_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac { {K}_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} (\cos ^2\alpha _0 - \sin ^2\alpha _0) \Big ) } . \\ \end{alignedat} \end{align}
We then obtain
 \begin{align} \begin{alignedat}{2} & \frac {\Im [ {\Psi }_{YY} ]_\mu }{| {\Psi }_{YY}|_\mu \bigg | 2 \frac { \text {d} {K}}{\text {d}\tau } {g} - 2 \frac { {K}^2}{ {\Psi }_{YY} } \Big ( \frac {\text {d}\alpha }{\text {d}\tau }\Big )^2 \bigg |_\mu } = \frac {K_0^2 L }{ 4 {K}_\mu }\frac { \sqrt { 2 \Im [\Psi _{yy0}]} }{ \big | \Psi _{yy0} \big | {W}_{Y\mu } } , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\Im [ {\Psi }_{YY} ]_\mu }{| {\Psi }_{YY}|_\mu \bigg | 2 \frac { \text {d} {K}}{\text {d}\tau } {g} - 2 \frac { {K}^2}{ {\Psi }_{YY} } \Big ( \frac {\text {d}\alpha }{\text {d}\tau }\Big )^2 \bigg |_\mu } = \frac {K_0^2 L }{ 4 {K}_\mu }\frac { \sqrt { 2 \Im [\Psi _{yy0}]} }{ \big | \Psi _{yy0} \big | {W}_{Y\mu } } , \\ \end{alignedat} \end{align}
where we have used
![]() ${W}_{Y\mu } = ({2/ \Im [ {\Psi }_{YY\mu }]})^{\frac {1}{2}}$
and
${W}_{Y\mu } = ({2/ \Im [ {\Psi }_{YY\mu }]})^{\frac {1}{2}}$
and
 \begin{align} \begin{alignedat}{2} & \Im [ {\Psi }_{YY\mu }] = \frac { \Im [\Psi _{yy0}] \frac { {K}_\mu ^2}{K_0^2} }{ \Big | \frac { {K}_{x\mu }}{K_0} + 2 \Psi _{yy0}^{\prime} \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac { {K}_{x\mu }}{K_0} + \sin ^2\alpha _0 - \frac { {K}_{x\mu }^2}{K_0^2} \Big ) \Big |^2 } . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \Im [ {\Psi }_{YY\mu }] = \frac { \Im [\Psi _{yy0}] \frac { {K}_\mu ^2}{K_0^2} }{ \Big | \frac { {K}_{x\mu }}{K_0} + 2 \Psi _{yy0}^{\prime} \Big ( \frac {\cos ^2\alpha _0 - \sin ^2\alpha _0}{\cos \alpha _0} \frac { {K}_{x\mu }}{K_0} + \sin ^2\alpha _0 - \frac { {K}_{x\mu }^2}{K_0^2} \Big ) \Big |^2 } . \\ \end{alignedat} \end{align}
With respect to the terms inside the exponential in (B.23), the
![]() $k_2$
-wavenumber resolution
$k_2$
-wavenumber resolution
![]() $\Delta {k}_{\mu 2}$
takes the following form:
$\Delta {k}_{\mu 2}$
takes the following form:
 \begin{align} & \Delta {k}_{\mu 2}^2 = \frac { 4 | {\Psi }_{YY\mu }|^2 }{ \Im [ {\Psi }_{YY\mu }] } = \\ & \frac { 4 }{ \Im [ \Psi _{yy0}^{\prime} ] } \frac { \Big | - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big ( \frac { {K}_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac { {K}_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} \big(\cos ^2\alpha _0 - \sin ^2\alpha _0 \big) \Big ) \Big |^2 }{ {K}_\mu ^6 / K_0^6 } \frac {K_0}{L} . \end{align}
\begin{align} & \Delta {k}_{\mu 2}^2 = \frac { 4 | {\Psi }_{YY\mu }|^2 }{ \Im [ {\Psi }_{YY\mu }] } = \\ & \frac { 4 }{ \Im [ \Psi _{yy0}^{\prime} ] } \frac { \Big | - \frac {1}{2} \sin ^2\alpha _0 + \Psi _{yy0}^{\prime} \Big ( \frac { {K}_x^3}{K_0^3} + 3\sin ^2\alpha _0 \frac { {K}_x}{K_0} - \frac {\sin ^2\alpha _0}{\cos \alpha _0} \big(\cos ^2\alpha _0 - \sin ^2\alpha _0 \big) \Big ) \Big |^2 }{ {K}_\mu ^6 / K_0^6 } \frac {K_0}{L} . \end{align}
Using (B.30) for
![]() $\Delta {k}_{\mu 2}$
and employing (B.25) and (B.27), the argument of the exponential in
$\Delta {k}_{\mu 2}$
and employing (B.25) and (B.27), the argument of the exponential in
![]() $|F_{xy,\mu }|^2$
(see (B.23)) can be written as
$|F_{xy,\mu }|^2$
(see (B.23)) can be written as
![]() $\exp [{-}h(k_x, k_y)]$
, where
$\exp [{-}h(k_x, k_y)]$
, where
 \begin{align} h(k_x, k_y) & = \frac { 2 \Big ( 2 \frac { \text {d} {K}}{ \text {d} \tau }\big |_\mu {g}_\mu \Big )^2}{ \bigg | \frac { \text {d} {K}}{ \text {d} \tau } {g} - 2 \frac { {K}^2}{ {\Psi }_{YY} } \Big ( \frac { \text {d} \alpha }{ \text {d} \tau }\Big )^2 \bigg |_\mu ^2} \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{\Delta {k}_{\mu 2}^2} \nonumber \\ & = \frac {K_0 L}{2} \frac {\Im [\Psi _{yy0}^{\prime}]}{ |\Psi _{yy0}^{\prime}|^2} \frac { {K}_{x\mu }^4}{ {K}_\mu ^4} \bigg ( \frac {k_y}{K_0} - \frac {k_x\sin {\alpha }_\mu }{K_0\cos {\alpha }_\mu } \bigg )^2 . \end{align}
\begin{align} h(k_x, k_y) & = \frac { 2 \Big ( 2 \frac { \text {d} {K}}{ \text {d} \tau }\big |_\mu {g}_\mu \Big )^2}{ \bigg | \frac { \text {d} {K}}{ \text {d} \tau } {g} - 2 \frac { {K}^2}{ {\Psi }_{YY} } \Big ( \frac { \text {d} \alpha }{ \text {d} \tau }\Big )^2 \bigg |_\mu ^2} \frac { \left ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \right )^2}{\Delta {k}_{\mu 2}^2} \nonumber \\ & = \frac {K_0 L}{2} \frac {\Im [\Psi _{yy0}^{\prime}]}{ |\Psi _{yy0}^{\prime}|^2} \frac { {K}_{x\mu }^4}{ {K}_\mu ^4} \bigg ( \frac {k_y}{K_0} - \frac {k_x\sin {\alpha }_\mu }{K_0\cos {\alpha }_\mu } \bigg )^2 . \end{align}
We express
![]() $h$
in normalised quantities to emphasise that
$h$
in normalised quantities to emphasise that
![]() $h$
is large,
$h$
is large,
![]() $h \sim K_0L \gg 1$
, unless
$h \sim K_0L \gg 1$
, unless
![]() $k_y \approx k_x \tan {\alpha }_\mu$
. The
$k_y \approx k_x \tan {\alpha }_\mu$
. The
![]() $k_y$
dependence of the integrand in (B.23) is through the exponential term (via
$k_y$
dependence of the integrand in (B.23) is through the exponential term (via
![]() $h$
) and through the turbulence spectrum
$h$
) and through the turbulence spectrum
![]() $\langle |\delta \hat {n} (k_x, k_y)|^2 \rangle _T$
. Given the assumption of large
$\langle |\delta \hat {n} (k_x, k_y)|^2 \rangle _T$
. Given the assumption of large
![]() $h$
, we can further simplify the expression for
$h$
, we can further simplify the expression for
![]() $|F_{xy,\mu }|^2$
by performing the
$|F_{xy,\mu }|^2$
by performing the
![]() $k_y$
integral using Laplace’s method (Bender & Orszag Reference Bender and Orszag1978). This leads to (3.9), which can be proven as follows. The Gaussian integral in
$k_y$
integral using Laplace’s method (Bender & Orszag Reference Bender and Orszag1978). This leads to (3.9), which can be proven as follows. The Gaussian integral in
![]() $k_y$
is dominated by contributions where
$k_y$
is dominated by contributions where
![]() $\partial h / \partial k_y \approx 0$
, which takes place for a given
$\partial h / \partial k_y \approx 0$
, which takes place for a given
![]() $k_{y\star }$
. This suggests expanding
$k_{y\star }$
. This suggests expanding
![]() $h$
around
$h$
around
![]() $k_{y\star }$
, giving
$k_{y\star }$
, giving
![]() $h(k_x, k_y) \approx h(k_x, k_{y\star }) + ({1}/{2}) (k_y - k_{y\star })^2 { \partial ^2 h }/{ \partial k_y^2 }\big |_{k_{y\star }}$
. To calculate
$h(k_x, k_y) \approx h(k_x, k_{y\star }) + ({1}/{2}) (k_y - k_{y\star })^2 { \partial ^2 h }/{ \partial k_y^2 }\big |_{k_{y\star }}$
. To calculate
![]() $\partial h / \partial k_y$
and
$\partial h / \partial k_y$
and
![]() $\partial ^2 h / \partial k_y^2$
, we first use (A.9) to express
$\partial ^2 h / \partial k_y^2$
, we first use (A.9) to express
![]() $\sin {\alpha }_\mu / \cos {\alpha }_\mu$
as a function of
$\sin {\alpha }_\mu / \cos {\alpha }_\mu$
as a function of
![]() ${K}_{x\mu }$
, giving
${K}_{x\mu }$
, giving
![]() $\sin {\alpha }_\mu /\cos {\alpha }_\mu = K_0 \sin \alpha _0/{K}_{x\mu }$
. Then, we employ the expression
$\sin {\alpha }_\mu /\cos {\alpha }_\mu = K_0 \sin \alpha _0/{K}_{x\mu }$
. Then, we employ the expression
![]() ${K}_{x\mu } \approx -k_x/2 + \sin \alpha _0(k_y + 2 K_0 \sin \alpha _0)K_0/k_x$
in (B.12), giving
${K}_{x\mu } \approx -k_x/2 + \sin \alpha _0(k_y + 2 K_0 \sin \alpha _0)K_0/k_x$
in (B.12), giving
![]() ${\partial {K}_{x\mu }}/{\partial k_y} \approx \sin \alpha _0 K_0/k_x$
. Using this, we find
${\partial {K}_{x\mu }}/{\partial k_y} \approx \sin \alpha _0 K_0/k_x$
. Using this, we find
 \begin{align} \begin{alignedat}{2} & \frac {\partial h}{ \partial k_y } \bigg |_{k_x, k_y} \approx L \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} \frac { {K}_{x\mu }^4}{ {K}_\mu ^4} \bigg ( \frac {k_y}{K_0} - k_x \frac {\sin \alpha _0}{ {K}_{x\mu }} \bigg ) \bigg ( 1 + \frac {K_0^2 \sin ^2\alpha _0}{ {K}_{x\mu }^2 } \bigg ) , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\partial h}{ \partial k_y } \bigg |_{k_x, k_y} \approx L \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} \frac { {K}_{x\mu }^4}{ {K}_\mu ^4} \bigg ( \frac {k_y}{K_0} - k_x \frac {\sin \alpha _0}{ {K}_{x\mu }} \bigg ) \bigg ( 1 + \frac {K_0^2 \sin ^2\alpha _0}{ {K}_{x\mu }^2 } \bigg ) , \\ \end{alignedat} \end{align}
where we have neglected terms small in
![]() $(k_y - k_x \tan {\alpha }_\mu )$
. The dominant contribution to the integral comes from
$(k_y - k_x \tan {\alpha }_\mu )$
. The dominant contribution to the integral comes from
![]() $k_{y}$
satisfying the extrema condition
$k_{y}$
satisfying the extrema condition
![]() $\partial h / \partial k_y = 0$
, which gives
$\partial h / \partial k_y = 0$
, which gives
where we used once more (B.12). Using (B.32), we calculate
![]() $\partial ^2 h / \partial k_y^2$
and evaluate it at
$\partial ^2 h / \partial k_y^2$
and evaluate it at
![]() $k_{y\star }$
, giving
$k_{y\star }$
, giving
 \begin{align} \begin{alignedat}{2} & \frac {\partial ^2 h} {\partial k_y^2} \bigg |_{k_x, k_y\star } = \frac {L}{K_0} \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} \frac { {K}_{x\mu \star }^4}{ {K}_{\mu \star }^4} \bigg ( 1 + \frac {K_0^2 \sin ^2\alpha _0}{ {K}_{x\mu \star }^2 } \bigg )^2 \approx \frac {L}{K_0} \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} = \frac {\Im [\Psi _{yy0}]}{ \big | \Psi _{yy0} \big |^2} . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\partial ^2 h} {\partial k_y^2} \bigg |_{k_x, k_y\star } = \frac {L}{K_0} \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} \frac { {K}_{x\mu \star }^4}{ {K}_{\mu \star }^4} \bigg ( 1 + \frac {K_0^2 \sin ^2\alpha _0}{ {K}_{x\mu \star }^2 } \bigg )^2 \approx \frac {L}{K_0} \frac {\Im [\Psi _{yy0}^{\prime}]}{ \big | \Psi _{yy0}^{\prime} \big |^2} = \frac {\Im [\Psi _{yy0}]}{ \big | \Psi _{yy0} \big |^2} . \\ \end{alignedat} \end{align}
Putting together (B.31) and (B.34), we find that the exponential term in (B.23),
![]() $\exp [{-}h(k_x, k_y)]$
, is given approximately by
$\exp [{-}h(k_x, k_y)]$
, is given approximately by
 \begin{align} \begin{alignedat}{2} & \exp \![{-}h(k_y)] \approx \exp\! \Bigg [ - \frac {\Im [\Psi _{yy0}]}{2 \big | \Psi _{yy0} \big |^2} (k_y + 2 K_0 \sin \alpha _0)^2 \Bigg ] = \exp\! \left [ \frac {- 2 (k_y + 2K_0\sin \alpha _0)^2}{\Delta k_y^2 } \right ] . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \exp \![{-}h(k_y)] \approx \exp\! \Bigg [ - \frac {\Im [\Psi _{yy0}]}{2 \big | \Psi _{yy0} \big |^2} (k_y + 2 K_0 \sin \alpha _0)^2 \Bigg ] = \exp\! \left [ \frac {- 2 (k_y + 2K_0\sin \alpha _0)^2}{\Delta k_y^2 } \right ] . \end{alignedat} \end{align}
Equation (B.35) is the Gaussian exponential term in
![]() $k_y$
in (3.9) and (3.10). In this expression, we recover the wavenumber resolution of the DBS diagnostic
$k_y$
in (3.9) and (3.10). In this expression, we recover the wavenumber resolution of the DBS diagnostic
![]() $\Delta k_y$
in Cartesian coordinates. Note the difference between
$\Delta k_y$
in Cartesian coordinates. Note the difference between
![]() $\Delta k_y$
in the lab frame, which is constant along the path and only depends on initial conditions, and
$\Delta k_y$
in the lab frame, which is constant along the path and only depends on initial conditions, and
![]() $\Delta k_{\mu 2}$
, which is the wavenumber resolution in the beam frame obtained by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), which depends strongly on the position along the path (see (B.30)). For the resolution in
$\Delta k_{\mu 2}$
, which is the wavenumber resolution in the beam frame obtained by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), which depends strongly on the position along the path (see (B.30)). For the resolution in
![]() $k_y$
, we find
$k_y$
, we find
![]() $\Delta k_y^2 = 4 | \Psi _{yy0}|^2 / \Im [\Psi _{yy0}]$
(see (3.10)), which simplifies to the particular case of
$\Delta k_y^2 = 4 | \Psi _{yy0}|^2 / \Im [\Psi _{yy0}]$
(see (3.10)), which simplifies to the particular case of
![]() $\Delta k_y = 2/\rho$
for the initial conditions chosen by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Note that the value
$\Delta k_y = 2/\rho$
for the initial conditions chosen by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). Note that the value
![]() $2 / \rho$
is simply a lower limit to the diagnostic wavenumber resolution. Putting (B.35) together with (B.28), we recover the full expression for
$2 / \rho$
is simply a lower limit to the diagnostic wavenumber resolution. Putting (B.35) together with (B.28), we recover the full expression for
![]() $|F_{xy,\mu }|^2$
in (3.9), including the
$|F_{xy,\mu }|^2$
in (3.9), including the
![]() $1/K_\mu W_{Y\mu }$
dependence outside of the exponential. Performing the integral over
$1/K_\mu W_{Y\mu }$
dependence outside of the exponential. Performing the integral over
![]() $k_y$
, we recover (3.8) for
$k_y$
, we recover (3.8) for
![]() $|F_{x\mu }|^2(k_x) = \int {\text {d}k_y} |F_{xy,\mu }|^2(k_x, k_y)$
.
$|F_{x\mu }|^2(k_x) = \int {\text {d}k_y} |F_{xy,\mu }|^2(k_x, k_y)$
.
Appendix C. Mapping the density between beam-aligned and Cartesian coordinates
In this appendix, we establish the relation between the beam-aligned representation of the density, as used by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ), and the Cartesian representation of the density that is employed by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). We note that the two representations are independent of beam-tracing or scattering physics, and are simply a manifestation of two different frames of reference in which to express the density fluctuations. The relation between the density expressed in both frames is used in Appendix D to state the equivalence between the Doppler backscattered amplitude of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ) and of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
We start from the definition of the beam-aligned representation of the density,
![]() $\delta \hat {n}_{b}$
, as given by (102) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). In the 2-D linear layer, it takes the following form:
$\delta \hat {n}_{b}$
, as given by (102) of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). In the 2-D linear layer, it takes the following form:
Here,
![]() $l$
and
$l$
and
![]() $Y$
are the two spatial dimensions that describe the small-scale fluctuations perpendicular to the background magnetic field and are aligned with the beam,
$Y$
are the two spatial dimensions that describe the small-scale fluctuations perpendicular to the background magnetic field and are aligned with the beam,
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are the corresponding Fourier-conjugate wavenumber components, and we assume no variation in the direction parallel to the magnetic field (
$k_2$
are the corresponding Fourier-conjugate wavenumber components, and we assume no variation in the direction parallel to the magnetic field (
![]() $u_{||}$
of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). The coordinate
$u_{||}$
of Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). The coordinate
![]() $l$
is the arc length of the central ray, given by (2.9). To improve clarity and to provide physical intuition, in this appendix, we use
$l$
is the arc length of the central ray, given by (2.9). To improve clarity and to provide physical intuition, in this appendix, we use
![]() $l$
as the parameter that the different functions depend on along the path, such as
$l$
as the parameter that the different functions depend on along the path, such as
![]() $x_c(l), \alpha (l)$
, etc. instead of
$x_c(l), \alpha (l)$
, etc. instead of
![]() $\tau$
as we have used in the main body of this manuscript.
$\tau$
as we have used in the main body of this manuscript.
We now turn to the Cartesian density-fluctuation field
![]() $\delta n$
given by (3.1), with
$\delta n$
given by (3.1), with
![]() $\mathbf {k}_\perp = k_x \hat {\mathbf {x}} + k_y \hat {\mathbf {y}}$
. The coordinates
$\mathbf {k}_\perp = k_x \hat {\mathbf {x}} + k_y \hat {\mathbf {y}}$
. The coordinates
![]() $(x,y)$
are related to
$(x,y)$
are related to
![]() $(l,Y)$
in (C.1) by
$(l,Y)$
in (C.1) by
![]() $ x = x_c(l) + Y \sin \alpha (l)$
,
$ x = x_c(l) + Y \sin \alpha (l)$
,
![]() $ y = y_c(l) - Y \cos \alpha (l)$
(see (3.2)). This gives the succinct form
$ y = y_c(l) - Y \cos \alpha (l)$
(see (3.2)). This gives the succinct form
![]() $(x,y) = \mathbf {q} + Y \hat {\mathbf {Y}}$
, where
$(x,y) = \mathbf {q} + Y \hat {\mathbf {Y}}$
, where
![]() $\mathbf {q} = (x_c, y_c)$
and
$\mathbf {q} = (x_c, y_c)$
and
![]() $k_xx + k_yy = \mathbf {k}_\perp \cdot \left ( \mathbf {q} + Y \hat {\mathbf {Y}} \right )$
.
$k_xx + k_yy = \mathbf {k}_\perp \cdot \left ( \mathbf {q} + Y \hat {\mathbf {Y}} \right )$
.
To relate the density-fluctuation spectra between beam-aligned and Cartesian coordinates in (C.1) and (3.1), we project one onto the other. We have
 \begin{align} \delta \hat {n}_{b} (k_1,k_2) &= \int \frac { \text {d}Y \text {d}l }{(2\pi )^2} \exp {({-} i k_1 l - i k_2 Y)} \ \delta {n}( \mathbf {r}) \nonumber \\ &= \int \frac { \text {d}k_x \text {d}k_y }{ (2\pi )^2 } \delta \hat {n}(k_x, k_y) \int \text {d}Y \text {d}l \exp \left [ i f_{\mathbf {k}_\perp }(l,Y) \right ], \end{align}
\begin{align} \delta \hat {n}_{b} (k_1,k_2) &= \int \frac { \text {d}Y \text {d}l }{(2\pi )^2} \exp {({-} i k_1 l - i k_2 Y)} \ \delta {n}( \mathbf {r}) \nonumber \\ &= \int \frac { \text {d}k_x \text {d}k_y }{ (2\pi )^2 } \delta \hat {n}(k_x, k_y) \int \text {d}Y \text {d}l \exp \left [ i f_{\mathbf {k}_\perp }(l,Y) \right ], \end{align}
where the function
![]() $f_{\mathbf {k}_\perp }(l,Y)$
is given by
$f_{\mathbf {k}_\perp }(l,Y)$
is given by
To find a useful relation between
![]() $\delta \hat {n}_b$
and
$\delta \hat {n}_b$
and
![]() $\delta \hat {n}$
, we proceed to compute the integrals in
$\delta \hat {n}$
, we proceed to compute the integrals in
![]() $l$
and
$l$
and
![]() $Y$
in (C.8). We do so by calculating the point of stationary phase in the 2-D
$Y$
in (C.8). We do so by calculating the point of stationary phase in the 2-D
![]() $(l,Y)$
plane. We note that the unit vectors
$(l,Y)$
plane. We note that the unit vectors
![]() $\hat {\mathbf {g}}$
and
$\hat {\mathbf {g}}$
and
![]() $\hat {\mathbf {Y}}$
both depend on
$\hat {\mathbf {Y}}$
both depend on
![]() $l$
, which needs to be taken into account when computing derivatives with respect to
$l$
, which needs to be taken into account when computing derivatives with respect to
![]() $l$
(see (B.7)). The point of the stationary phase
$l$
(see (B.7)). The point of the stationary phase
![]() $(l_b, Y_b)$
is given by the joint conditions
$(l_b, Y_b)$
is given by the joint conditions
![]() $\partial f_{\mathbf {k}_\perp } /\partial l |_{l_b,Y_b} = \partial f_{\mathbf {k}_\perp } /\partial Y |_{l_b,Y_b} = 0$
. Using (B.7), the derivatives of
$\partial f_{\mathbf {k}_\perp } /\partial l |_{l_b,Y_b} = \partial f_{\mathbf {k}_\perp } /\partial Y |_{l_b,Y_b} = 0$
. Using (B.7), the derivatives of
![]() $f_{\mathbf {k}_\perp }$
with respect to
$f_{\mathbf {k}_\perp }$
with respect to
![]() $l$
and
$l$
and
![]() $Y$
are given by
$Y$
are given by
 \begin{align} \begin{alignedat}{2} & \frac {\partial f_{\mathbf {k}_\perp } }{\partial l} = \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \left ( 1 + Y \frac {\text {d}\alpha }{\text {d}l} \right ) - k_1, \\ & \frac {\partial f_{\mathbf {k}_\perp } }{\partial Y} = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} - k_2 , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\partial f_{\mathbf {k}_\perp } }{\partial l} = \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \left ( 1 + Y \frac {\text {d}\alpha }{\text {d}l} \right ) - k_1, \\ & \frac {\partial f_{\mathbf {k}_\perp } }{\partial Y} = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} - k_2 , \end{alignedat} \end{align}
where we used the definition of
![]() $\mathbf {g} = \text {d}\mathbf {q}/\text {d}\tau$
and
$\mathbf {g} = \text {d}\mathbf {q}/\text {d}\tau$
and
![]() $\text {d}l = g \text {d}\tau$
. The point of the stationary phase
$\text {d}l = g \text {d}\tau$
. The point of the stationary phase
![]() $(l_b, Y_b)$
is determined by
$(l_b, Y_b)$
is determined by
 \begin{align} \begin{alignedat}{2} & k_1 = \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b \left ( 1 + Y_b \frac {\text {d}\alpha }{\text {d}l}\Big |_b \right ), \\ & k_2 = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_b , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & k_1 = \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b \left ( 1 + Y_b \frac {\text {d}\alpha }{\text {d}l}\Big |_b \right ), \\ & k_2 = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_b , \end{alignedat} \end{align}
where the subscript
![]() $(.)_b$
means that functions are evaluated at
$(.)_b$
means that functions are evaluated at
![]() $(l_b, Y_b)$
. It is worth commenting on the implications from (C.5). Given the dependence of
$(l_b, Y_b)$
. It is worth commenting on the implications from (C.5). Given the dependence of
![]() $\hat {\mathbf {g}}$
and
$\hat {\mathbf {g}}$
and
![]() $\hat {\mathbf {Y}}$
on
$\hat {\mathbf {Y}}$
on
![]() $l$
, for a given
$l$
, for a given
![]() $\mathbf {k}_\perp$
, the second equation in (C.5) states that the value of
$\mathbf {k}_\perp$
, the second equation in (C.5) states that the value of
![]() $k_2$
determines the location
$k_2$
determines the location
![]() $l_b$
where (C.5) is satisfied. Equivalently, given
$l_b$
where (C.5) is satisfied. Equivalently, given
![]() $\mathbf {k}_\perp$
,
$\mathbf {k}_\perp$
,
![]() $k_2$
is determined uniquely by the location along the path
$k_2$
is determined uniquely by the location along the path
![]() $l_b$
, independently of the coordinate
$l_b$
, independently of the coordinate
![]() $Y_b$
. Having determined
$Y_b$
. Having determined
![]() $l_b$
, the value of
$l_b$
, the value of
![]() $k_1$
then determines the location
$k_1$
then determines the location
![]() $Y_b$
where
$Y_b$
where
![]() $(k_1, k_2)$
and
$(k_1, k_2)$
and
![]() $\mathbf {k}_\perp$
are resonant. Or yet equivalently, given
$\mathbf {k}_\perp$
are resonant. Or yet equivalently, given
![]() $\mathbf {k}_\perp$
and
$\mathbf {k}_\perp$
and
![]() $l_b$
,
$l_b$
,
![]() $k_1$
is determined by the location perpendicular to the central ray
$k_1$
is determined by the location perpendicular to the central ray
![]() $Y_b$
.
$Y_b$
.
Having calculated the location
![]() $(l_b,Y_b)$
and the relation between
$(l_b,Y_b)$
and the relation between
![]() ${\mathbf {k}}_\perp$
and
${\mathbf {k}}_\perp$
and
![]() $(k_1, k_2)$
, next we want to approximate
$(k_1, k_2)$
, next we want to approximate
![]() $f_{\mathbf {k}_\perp }$
quadratically in
$f_{\mathbf {k}_\perp }$
quadratically in
![]() $(l-l_b)$
and
$(l-l_b)$
and
![]() $(Y-Y_b)$
. For that, we turn to compute the second derivatives of
$(Y-Y_b)$
. For that, we turn to compute the second derivatives of
![]() $f_{\mathbf {k}_\perp }$
with respect to
$f_{\mathbf {k}_\perp }$
with respect to
![]() $l$
and
$l$
and
![]() $Y$
, which are given by
$Y$
, which are given by
 \begin{align} \begin{alignedat}{2} & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l^2} = - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \frac {\text {d}\alpha }{\text {d}l} + Y \left ( - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \left ( \frac {\text {d}\alpha }{\text {d}l} \right )^2 + \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \frac {\text {d}^2\alpha }{\text {d}l^2} \right ), \\ & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l \partial Y} = \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \frac {\text {d}\alpha }{\text {d}l} , \\ & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial Y^2} = 0 . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l^2} = - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \frac {\text {d}\alpha }{\text {d}l} + Y \left ( - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}} \left ( \frac {\text {d}\alpha }{\text {d}l} \right )^2 + \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \frac {\text {d}^2\alpha }{\text {d}l^2} \right ), \\ & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l \partial Y} = \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \frac {\text {d}\alpha }{\text {d}l} , \\ & \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial Y^2} = 0 . \\ \end{alignedat} \end{align}
Using (C.6), we can write
 \begin{align} \begin{alignedat}{2} f_{\mathbf {k}_\perp }(l,Y) \approx f_{\mathbf {k}_\perp }({l_b,Y_b}) + \frac {(l-l_b)^2}{2} \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l^2}\bigg |_{l_b,Y_b} + {(l-l_b)(Y-Y_b)} \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l \partial Y}\bigg |_{l_b,Y_b} . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} f_{\mathbf {k}_\perp }(l,Y) \approx f_{\mathbf {k}_\perp }({l_b,Y_b}) + \frac {(l-l_b)^2}{2} \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l^2}\bigg |_{l_b,Y_b} + {(l-l_b)(Y-Y_b)} \frac {\partial ^2 f_{\mathbf {k}_\perp } }{\partial l \partial Y}\bigg |_{l_b,Y_b} . \end{alignedat} \end{align}
Computing the Gaussian integrals in
![]() $l$
and
$l$
and
![]() $Y$
using (C.7), we find the desired relation between
$Y$
using (C.7), we find the desired relation between
![]() $\delta \hat {n}(\mathbf {k}_\perp )$
and
$\delta \hat {n}(\mathbf {k}_\perp )$
and
![]() $\delta \hat {n}_b(k_1,k_2)$
,
$\delta \hat {n}_b(k_1,k_2)$
,
This is the general relation between
![]() $\delta \hat {n}_b$
and
$\delta \hat {n}_b$
and
![]() $\delta \hat {n}$
in two dimensions. In the next section, we use (C.8) to prove the equivalence between the backscattering amplitude in two dimensions using a beam-aligned
$\delta \hat {n}$
in two dimensions. In the next section, we use (C.8) to prove the equivalence between the backscattering amplitude in two dimensions using a beam-aligned
![]() $\delta \hat {n}_b$
, as done by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), and using a Cartesian
$\delta \hat {n}_b$
, as done by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), and using a Cartesian
![]() $\delta \hat {n}$
, as done by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
$\delta \hat {n}$
, as done by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017).
Appendix D. Relation of the scattered amplitude
 $A_r$
between beam-aligned and Cartesian coordinates
$A_r$
between beam-aligned and Cartesian coordinates
In this appendix, we show the equivalence between the scattered amplitude
![]() $A_r$
in beam-aligned coordinates, as used by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), and Cartesian coordinates, as in (3.3) and used by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). This shows that both the beam-tracing model of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) are equivalent to each other: they are simply expressed in different frames of reference. A similar exercise for directly mapping the DBS power between both representations requires further work, which will be the subject of a future publication.
$A_r$
in beam-aligned coordinates, as used by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
), and Cartesian coordinates, as in (3.3) and used by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017). This shows that both the beam-tracing model of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and the 2-D DBS model of Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) are equivalent to each other: they are simply expressed in different frames of reference. A similar exercise for directly mapping the DBS power between both representations requires further work, which will be the subject of a future publication.
We start from the expression of the backscattered amplitude of (169) from Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022 Reference Hall-Chen, Parra and Hillesheimb ), which in the 2-D linear layer takes the following form:
where
![]() $F_{\nu }$
is the effective filter function in beam-aligned coordinates and is given by
$F_{\nu }$
is the effective filter function in beam-aligned coordinates and is given by
 \begin{align} \begin{alignedat}{2} & F_\nu (k_1, k_2) = &&- \left [ \frac { i\pi }{ \frac {\text {d}K}{ \text {d} \tau } g } \frac { \Im [{\Psi }_{YY}] }{ \Psi _{YY} } \right ]^{\frac {1}{2}}_\nu \frac { \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ]_\nu }{n_\nu } \exp \bigg ( {i2\phi _{G\nu } } - \frac {i}{4} \frac {k_2^2}{\Psi _{YY\nu }} \bigg ) . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & F_\nu (k_1, k_2) = &&- \left [ \frac { i\pi }{ \frac {\text {d}K}{ \text {d} \tau } g } \frac { \Im [{\Psi }_{YY}] }{ \Psi _{YY} } \right ]^{\frac {1}{2}}_\nu \frac { \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ]_\nu }{n_\nu } \exp \bigg ( {i2\phi _{G\nu } } - \frac {i}{4} \frac {k_2^2}{\Psi _{YY\nu }} \bigg ) . \end{alignedat} \end{align}
The notation
![]() $[{.}]_\nu$
means that functions of
$[{.}]_\nu$
means that functions of
![]() $\tau$
have been evaluated at
$\tau$
have been evaluated at
![]() ${\tau }_\nu$
, the location along the central-ray path where the Bragg condition for backscattering is satisfied. In beam-aligned coordinates, the Bragg condition is
${\tau }_\nu$
, the location along the central-ray path where the Bragg condition for backscattering is satisfied. In beam-aligned coordinates, the Bragg condition is
Note that only the lowest-order contribution
![]() $\sim 1/\lambda$
to the Bragg condition has been kept here. For a given
$\sim 1/\lambda$
to the Bragg condition has been kept here. For a given
![]() $k_1$
, there can exist several
$k_1$
, there can exist several
![]() ${\tau }_\nu$
associated to it. This explains the sum
${\tau }_\nu$
associated to it. This explains the sum
![]() $\sum _\nu$
in (D.1). The scattering amplitude in (D.1) only has contributions from backscattering events. Any forward scattering component is absent because of the Bragg condition.
$\sum _\nu$
in (D.1). The scattering amplitude in (D.1) only has contributions from backscattering events. Any forward scattering component is absent because of the Bragg condition.
We note that
![]() ${\tau }_\nu$
differs from the
${\tau }_\nu$
differs from the
![]() $\tau _\mu$
calculated using Cartesian coordinates throughout the manuscript by a correction of order
$\tau _\mu$
calculated using Cartesian coordinates throughout the manuscript by a correction of order
![]() $\sim W/\lambda$
, which we calculate later in this appendix. This difference between
$\sim W/\lambda$
, which we calculate later in this appendix. This difference between
![]() $\tau _\mu$
and
$\tau _\mu$
and
![]() $\tau _\nu$
is of limited importance in the main text of this manuscript, but it is important to consider in order to show the equivalence of the scattered amplitude in both representations.
$\tau _\nu$
is of limited importance in the main text of this manuscript, but it is important to consider in order to show the equivalence of the scattered amplitude in both representations.
To show that the formulae for the scattered amplitude in Cartesian and beam-aligned coordinates are equivalent, we make use of (C.8) and insert it into (D.1) for the amplitude. By exchanging the order of integration, we have
 \begin{align} \begin{alignedat}{2} & {A}_r(t) =&& -A_{ant} \sum _\nu \int \frac { \text {d}k_x \text {d}k_y }{2\pi } {\delta \hat {n}({k}_x, k_y)} \int \frac {\text {d}k_1 \text {d}k_2}{| \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha /\text {d}l |_b} \left [ \frac { i\pi }{ \frac {\text {d}K}{ \text {d} \tau } g } \frac { \Im [{\Psi }_{YY}] }{ \Psi _{YY} } \right ]^{\frac {1}{2}}_\nu \\ & && \times \frac { \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ]_\nu }{n_\nu } \exp \left ( i 2\phi _{G\nu } \right ) \exp \big [i f \big ], \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & {A}_r(t) =&& -A_{ant} \sum _\nu \int \frac { \text {d}k_x \text {d}k_y }{2\pi } {\delta \hat {n}({k}_x, k_y)} \int \frac {\text {d}k_1 \text {d}k_2}{| \mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha /\text {d}l |_b} \left [ \frac { i\pi }{ \frac {\text {d}K}{ \text {d} \tau } g } \frac { \Im [{\Psi }_{YY}] }{ \Psi _{YY} } \right ]^{\frac {1}{2}}_\nu \\ & && \times \frac { \Big [ {\hat {\textbf{e}}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\textbf{e}}} \Big ]_\nu }{n_\nu } \exp \left ( i 2\phi _{G\nu } \right ) \exp \big [i f \big ], \\ \end{alignedat} \end{align}
where the phase
![]() $f$
is given by
$f$
is given by
We recall from Appendix C that the subscript
![]() $(.)_b$
corresponds to the location
$(.)_b$
corresponds to the location
![]() $(l_b, Y_b)$
where the resonance condition in (C.5) takes place. We proceed to calculate the integrals in
$(l_b, Y_b)$
where the resonance condition in (C.5) takes place. We proceed to calculate the integrals in
![]() $k_1$
and
$k_1$
and
![]() $k_2$
by the method of stationary phase (Bender & Orszag Reference Bender and Orszag1978).
$k_2$
by the method of stationary phase (Bender & Orszag Reference Bender and Orszag1978).
The phase
![]() $f$
in (D.5) is made of a large piece,
$f$
in (D.5) is made of a large piece,
![]() $2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_b + k_1 (l_\nu - l_b) \sim L/\lambda$
, and a small piece,
$2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_b + k_1 (l_\nu - l_b) \sim L/\lambda$
, and a small piece,
![]() $- {k_2^2}/{4 \Psi _{YY\nu }} \sim 1$
. The large piece forces
$- {k_2^2}/{4 \Psi _{YY\nu }} \sim 1$
. The large piece forces
![]() $l_\nu - l_b \ll L$
. One can see this by using the stationary-phase method. Indeed,
$l_\nu - l_b \ll L$
. One can see this by using the stationary-phase method. Indeed,
![]() $\partial f/\partial k_1 =0$
and
$\partial f/\partial k_1 =0$
and
![]() $\partial f/\partial k_2 =0$
give
$\partial f/\partial k_2 =0$
give
![]() $l_b = l_\nu$
to lowest order.
$l_b = l_\nu$
to lowest order.
We proceed by assuming
![]() $l_\nu - l_b \sim W$
. We can then find the distance between a nearby point
$l_\nu - l_b \sim W$
. We can then find the distance between a nearby point
![]() $l_\nu$
to
$l_\nu$
to
![]() $l_b$
. We can expand
$l_b$
. We can expand
![]() $\hat {\mathbf {Y}}_\nu - \hat {\mathbf {Y}}_b$
as
$\hat {\mathbf {Y}}_\nu - \hat {\mathbf {Y}}_b$
as
![]() $\hat {\mathbf {Y}}_\nu - \hat {\mathbf {Y}}_b \approx (l_\nu -l_b) {\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_b$
. Multiplying by
$\hat {\mathbf {Y}}_\nu - \hat {\mathbf {Y}}_b \approx (l_\nu -l_b) {\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_b$
. Multiplying by
![]() $\mathbf {k}_\perp$
and using (B.7), (C.5) and
$\mathbf {k}_\perp$
and using (B.7), (C.5) and
![]() ${\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_b \approx {\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_\nu$
, we find
${\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_b \approx {\text {d} \hat {\mathbf {Y}}}/{\text {d}l}|_\nu$
, we find
which results in
![]() $l_\nu - l_b \sim W$
as we predicted above. Equation (D.6) also shows that, for a given
$l_\nu - l_b \sim W$
as we predicted above. Equation (D.6) also shows that, for a given
![]() $\mathbf {k}_\perp$
, we can change
$\mathbf {k}_\perp$
, we can change
![]() $k_2$
by moving in
$k_2$
by moving in
![]() $l_b$
. A similar exercise can be done for
$l_b$
. A similar exercise can be done for
![]() $\hat {\mathbf {g}}_\nu$
, which gives
$\hat {\mathbf {g}}_\nu$
, which gives
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b \approx - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_b ({\text {d}\alpha }/{\text {d}l})|_b (l_\nu - l_b) - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b ({\text {d}\alpha }/{\text {d}l})^2|_b (l_\nu - l_b)^2/2 \sim 1/L$
. In this case, we can use
$\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b \approx - \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_b ({\text {d}\alpha }/{\text {d}l})|_b (l_\nu - l_b) - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b ({\text {d}\alpha }/{\text {d}l})^2|_b (l_\nu - l_b)^2/2 \sim 1/L$
. In this case, we can use
![]() $\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \approx \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b$
.
$\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \approx \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_b$
.
We now Taylor-expand
![]() $\mathbf {q}_b$
in (D.5) in powers of
$\mathbf {q}_b$
in (D.5) in powers of
![]() $l_b - l_\nu$
. Using
$l_b - l_\nu$
. Using
![]() $\text {d}\mathbf {q}/\text {d}l = \hat {\mathbf {g}}$
and (B.7), we have
$\text {d}\mathbf {q}/\text {d}l = \hat {\mathbf {g}}$
and (B.7), we have
Next, we use (D.6) and (D.7) to find a suitable expression of the phase in (D.5) in terms of powers of
![]() $l_b - l_\nu$
, keeping terms up to
$l_b - l_\nu$
, keeping terms up to
![]() $\sim 1$
. We find
$\sim 1$
. We find
 \begin{align} \begin{alignedat}{2} & f \approx && \ 2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu -\! \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu )^2}{4 \Psi _{YY\nu }} - \!\left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu + \frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu ) (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) (\text {d}\alpha / \text {d}l )_\nu }{2 \Psi _{YY\nu }} \right ) \!(l_b - l_\nu ) \\ & && - \frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 }{4\Psi _{YY\nu } } {(l_b - l_\nu )^2}. \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & f \approx && \ 2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu -\! \frac {(\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu )^2}{4 \Psi _{YY\nu }} - \!\left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu + \frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu ) (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) (\text {d}\alpha / \text {d}l )_\nu }{2 \Psi _{YY\nu }} \right ) \!(l_b - l_\nu ) \\ & && - \frac { (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 }{4\Psi _{YY\nu } } {(l_b - l_\nu )^2}. \end{alignedat} \end{align}
Note that the dependence on
![]() $k_2$
in (D.4) is now hidden in
$k_2$
in (D.4) is now hidden in
![]() $l_b$
through (D.6).
$l_b$
through (D.6).
We compute the
![]() $k_2$
integral in (D.4) by changing variables of integration from
$k_2$
integral in (D.4) by changing variables of integration from
![]() $k_2$
to
$k_2$
to
![]() $l_b$
by
$l_b$
by
![]() $\text {d}k_2 = |\mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha / \text {d}l |_b \text {d}l_b$
. The integral in
$\text {d}k_2 = |\mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha / \text {d}l |_b \text {d}l_b$
. The integral in
![]() $l_b$
is a complex Gaussian. We find
$l_b$
is a complex Gaussian. We find
 \begin{align} \begin{alignedat}{2} & \int && \frac {\text {d}k_2}{|\mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha / \text {d}l |_b } \exp \left [ i f \right ] = \left ( \frac {- 4 i \pi \Psi _{YY\nu } }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } \right )^{\frac {1}{2}} \exp \left [ i h_\nu (k_1) \right ] , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \int && \frac {\text {d}k_2}{|\mathbf {k}_\perp \cdot \hat {\mathbf {g}} \ \text {d}\alpha / \text {d}l |_b } \exp \left [ i f \right ] = \left ( \frac {- 4 i \pi \Psi _{YY\nu } }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } \right )^{\frac {1}{2}} \exp \left [ i h_\nu (k_1) \right ] , \end{alignedat} \end{align}
where the function
![]() $h_\nu (k_1)$
is given by
$h_\nu (k_1)$
is given by
 \begin{align} \begin{alignedat}{2} & h_\nu (k_1) = 2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu + \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \ (\text {d}\alpha / \text {d}l)_\nu } + \frac { \Psi _{YY\nu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & h_\nu (k_1) = 2 s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu + \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \ (\text {d}\alpha / \text {d}l)_\nu } + \frac { \Psi _{YY\nu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } . \\ \end{alignedat} \end{align}
Having completed the
![]() $k_2$
integral, (D.4) now takes the following form:
$k_2$
integral, (D.4) now takes the following form:
 \begin{align} \begin{alignedat}{2} & {A}_r(t) =&& -A_{ant} \sum _\nu \int { \text {d}k_x \text {d}k_y } \ {\delta \hat {n}({k}_x, k_y)} \int {\text {d}k_1} \left [ \frac { \Im [{\Psi }_{YY}] }{\left (g {\text {d}K}/{ \text {d} \tau } \right ) (\mathbf {k}_\perp \cdot \hat {\mathbf {g}})^2 (\text {d}\alpha /\text {d}l)^2 } \right ]^{\frac {1}{2}}_\nu \\ & && \times \frac { \Big [ {\hat {\mathbf e}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\mathbf e}} \Big ]_\nu }{n_\nu } \exp \left ( i 2\phi _{G\nu } \right ) \exp \left [ i h_\nu (k_1) \right ]. \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & {A}_r(t) =&& -A_{ant} \sum _\nu \int { \text {d}k_x \text {d}k_y } \ {\delta \hat {n}({k}_x, k_y)} \int {\text {d}k_1} \left [ \frac { \Im [{\Psi }_{YY}] }{\left (g {\text {d}K}/{ \text {d} \tau } \right ) (\mathbf {k}_\perp \cdot \hat {\mathbf {g}})^2 (\text {d}\alpha /\text {d}l)^2 } \right ]^{\frac {1}{2}}_\nu \\ & && \times \frac { \Big [ {\hat {\mathbf e}}^* \cdot ( \boldsymbol {\epsilon }_{eq} - \boldsymbol {1} ) \cdot {\hat {\mathbf e}} \Big ]_\nu }{n_\nu } \exp \left ( i 2\phi _{G\nu } \right ) \exp \left [ i h_\nu (k_1) \right ]. \\ \end{alignedat} \end{align}
Note that the integrand under the
![]() $k_1$
integral sign in (D.11) has a non-trivial dependence on
$k_1$
integral sign in (D.11) has a non-trivial dependence on
![]() $k_1$
through the Bragg condition
$k_1$
through the Bragg condition
![]() $k_1 = - 2 K_\nu$
in (D.3). However, the integral can be simplified by noting that
$k_1 = - 2 K_\nu$
in (D.3). However, the integral can be simplified by noting that
![]() $k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \sim 1/W$
. This follows from the Bragg conditions (3.4) and (D.3) and the exponential term in (D.9). Computing the difference between (3.4) and (D.3), we find
$k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \sim 1/W$
. This follows from the Bragg conditions (3.4) and (D.3) and the exponential term in (D.9). Computing the difference between (3.4) and (D.3), we find
Since
![]() $k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \sim 1/W$
, to make the exponential term in (D.9) of order unity, we find
$k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \sim 1/W$
, to make the exponential term in (D.9) of order unity, we find
![]() $l_\nu - l_\mu \sim W$
and we Taylor-expand terms in
$l_\nu - l_\mu \sim W$
and we Taylor-expand terms in
![]() $h_\nu$
in powers of
$h_\nu$
in powers of
![]() $(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )$
. When calculating
$(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )$
. When calculating
![]() $\text {d}h_\nu /\text {d}k_1$
and
$\text {d}h_\nu /\text {d}k_1$
and
![]() $\text {d}^2h_\nu /\text {d}k_1^2$
, we will make use of (D.12), so that terms that are functions of
$\text {d}^2h_\nu /\text {d}k_1^2$
, we will make use of (D.12), so that terms that are functions of
![]() $l_\nu$
can be calculated by using the chain rule
$l_\nu$
can be calculated by using the chain rule
Equation (D.13) is particularly useful for computing
![]() $\text {d} (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )/\text {d}k_1$
and
$\text {d} (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )/\text {d}k_1$
and
![]() $\text {d} ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu )/\text {d}k_1$
. Using (B.7) and (D.13) , we have
$\text {d} ( \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu )/\text {d}k_1$
. Using (B.7) and (D.13) , we have
 \begin{align} \begin{alignedat}{2} & \frac {\text {d} ( \mathbf {k}_\perp \cdot \hat { \mathbf {g}}_\nu ) }{\text {d}k_1} = \frac { ({\text {d} \alpha }/{ \text {d}l)_\nu } }{2(\text {d}K/\text {d}l)_\nu } \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu \sim \frac {\lambda }{W} \ll 1 , \\ & \frac {\text {d} ( \mathbf {k}_\perp \cdot \hat { \mathbf {Y}}_\nu ) }{\text {d}k_1} = - \frac { ({\text {d} \alpha }/{ \text {d}l)_\nu } }{2(\text {d}K/\text {d}l)_\nu } \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \sim 1 , \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac {\text {d} ( \mathbf {k}_\perp \cdot \hat { \mathbf {g}}_\nu ) }{\text {d}k_1} = \frac { ({\text {d} \alpha }/{ \text {d}l)_\nu } }{2(\text {d}K/\text {d}l)_\nu } \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu \sim \frac {\lambda }{W} \ll 1 , \\ & \frac {\text {d} ( \mathbf {k}_\perp \cdot \hat { \mathbf {Y}}_\nu ) }{\text {d}k_1} = - \frac { ({\text {d} \alpha }/{ \text {d}l)_\nu } }{2(\text {d}K/\text {d}l)_\nu } \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \sim 1 , \end{alignedat} \end{align}
where we have employed
![]() $\mathbf {k}_\perp \cdot \hat { \mathbf {Y}}_\nu \sim 1/W$
. Using (D.12), (D.13) and (D.14), the large phase term
$\mathbf {k}_\perp \cdot \hat { \mathbf {Y}}_\nu \sim 1/W$
. Using (D.12), (D.13) and (D.14), the large phase term
![]() $2s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu$
can be expanded as
$2s_\nu + \mathbf {k}_\perp \cdot \mathbf {q}_\nu$
can be expanded as
where we have used the Bragg condition
![]() $2 K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \approx 0$
. Next, we expand the third and fourth terms of
$2 K_\mu + \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \approx 0$
. Next, we expand the third and fourth terms of
![]() $h_\nu$
in (D.10). We have
$h_\nu$
in (D.10). We have
 \begin{align} \begin{alignedat}{2} & \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \ (\text {d}\alpha / \text {d}l)_\nu } = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \frac {k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \ (\text {d}\alpha / \text {d}l)_\mu } - \frac { (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2 }{ 2 (\text {d}K / \text {d}l)_\mu } + O\left ( \frac {\lambda }{W} \right ) , \\ & \frac { \Psi _{YY\nu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } = \frac { \Psi _{YY\mu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2 (\text {d}\alpha /\text {d}l)_\mu ^2 } + O\left ( \frac {\lambda }{W} \right ) . \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\nu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \ (\text {d}\alpha / \text {d}l)_\nu } = \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu \frac {k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \ (\text {d}\alpha / \text {d}l)_\mu } - \frac { (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2 }{ 2 (\text {d}K / \text {d}l)_\mu } + O\left ( \frac {\lambda }{W} \right ) , \\ & \frac { \Psi _{YY\nu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\nu )^2 (\text {d}\alpha /\text {d}l)_\nu ^2 } = \frac { \Psi _{YY\mu } \left ( k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \right )^2 }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2 (\text {d}\alpha /\text {d}l)_\mu ^2 } + O\left ( \frac {\lambda }{W} \right ) . \\ \end{alignedat} \end{align}
The phase
![]() $h_\nu$
now has explicit dependence on
$h_\nu$
now has explicit dependence on
![]() $(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )$
and it is given by
$(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )$
and it is given by
 \begin{align} \begin{alignedat}{2} & h_\nu = 2 s_\mu + \mathbf {k}_\perp \cdot \mathbf {q}_\mu + \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \ (\text {d}\alpha / \text {d}l)_\mu } + \frac { \text {d}^2 h_\nu }{ \text {d} k_1^2 } \bigg |_{\mu } \frac {(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2}{2} + O\left ( \frac {\lambda }{W} \right ) , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} & h_\nu = 2 s_\mu + \mathbf {k}_\perp \cdot \mathbf {q}_\mu + \frac { \mathbf {k}_\perp \cdot \hat {\mathbf {Y}}_\mu (k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu ) }{ \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu \ (\text {d}\alpha / \text {d}l)_\mu } + \frac { \text {d}^2 h_\nu }{ \text {d} k_1^2 } \bigg |_{\mu } \frac {(k_1 - \mathbf {k}_\perp \cdot \hat {\mathbf {g}}_\mu )^2}{2} + O\left ( \frac {\lambda }{W} \right ) , \\ \end{alignedat} \end{align}
where
![]() $ { \text {d}^2 h_\nu }/{ \text {d} k_1^2 }\big |_{\mu } \sim L \lambda$
is given by
$ { \text {d}^2 h_\nu }/{ \text {d} k_1^2 }\big |_{\mu } \sim L \lambda$
is given by
 \begin{align} \begin{alignedat}{2} \frac { \text {d}^2 h_\nu }{ \text {d} k_1^2 } \bigg |_{\mu } = \frac { 2 \Psi _{YY\mu } }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_{\mu })^2 (\text {d}\alpha /\text {d}l)_{\mu }^2 } - \frac {1}{2 (\text {d}K/ \text {d}l)_{\mu }} . \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} \frac { \text {d}^2 h_\nu }{ \text {d} k_1^2 } \bigg |_{\mu } = \frac { 2 \Psi _{YY\mu } }{ (\mathbf {k}_\perp \cdot \hat {\mathbf {g}}_{\mu })^2 (\text {d}\alpha /\text {d}l)_{\mu }^2 } - \frac {1}{2 (\text {d}K/ \text {d}l)_{\mu }} . \end{alignedat} \end{align}
With this approximation to
![]() $h_\nu$
, the integral over
$h_\nu$
, the integral over
![]() $k_1$
in (D.11) becomes a Gaussian integral that can be easily evaluated. We find that the integral in
$k_1$
in (D.11) becomes a Gaussian integral that can be easily evaluated. We find that the integral in
![]() $k_1$
in (D.11) recovers (B.17) and (B.18). This is proof that the representations of the density in beam-aligned coordinates used by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and in Cartesian coordinates used by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) are completely equivalent.
$k_1$
in (D.11) recovers (B.17) and (B.18). This is proof that the representations of the density in beam-aligned coordinates used by Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) and in Cartesian coordinates used by Gusakov et al. (Reference Gusakov, Irzak and Popov2014, Reference Gusakov, Irzak, Popov, Khitrov and Teplova2017) are completely equivalent.
We note that the equivalence obtained here between the beam-aligned and Cartesian representation of the density is proven for the scattered amplitude and not directly for the power. It is possible to directly prove the equivalence in the scattered power from the beam-aligned expression in
![]() $(k_1,k_2)$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) to the Cartesian expression in
$(k_1,k_2)$
of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) to the Cartesian expression in
![]() $(k_x, k_y)$
in (3.7), (3.8). This requires mapping the correlation functions between beam-aligned
$(k_x, k_y)$
in (3.7), (3.8). This requires mapping the correlation functions between beam-aligned
![]() $\hat {C}_b$
and Cartesian coordinates
$\hat {C}_b$
and Cartesian coordinates
![]() $\hat {C}$
, which is non-trivial and will be the subject of a future publication.
$\hat {C}$
, which is non-trivial and will be the subject of a future publication.
It is worth commenting on the equivalence of the scattered-power contributions for beam-aligned and Cartesian coordinates when regarded as a one-dimensional integral in
![]() $k_x$
or
$k_x$
or
![]() $k_1$
. In this case, it is straightforward to directly map the Cartesian and beam-aligned representations of the scattered power, as follows.
$k_1$
. In this case, it is straightforward to directly map the Cartesian and beam-aligned representations of the scattered power, as follows.
The backscattered power in Cartesian coordinates from (3.9) can be rewritten as an integral over the beam-aligned
![]() $k_1$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). To express the one-dimensional integral in (3.9) in terms of
$k_1$
(Hall-Chen et al. Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
). To express the one-dimensional integral in (3.9) in terms of
![]() $k_1$
, change variables using
$k_1$
, change variables using
![]() $\text {d}k_x = \text {d}k_1 K_\mu / |K_{x\mu }| = \text {d}k_1/|\cos \alpha _\mu |$
, where we used (A.9). We find
$\text {d}k_x = \text {d}k_1 K_\mu / |K_{x\mu }| = \text {d}k_1/|\cos \alpha _\mu |$
, where we used (A.9). We find
 \begin{align} \begin{alignedat}{2} &\frac {p_r}{P_{ant}} &&\approx \pi ^{\frac {3}{2}} K_0L \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \sum _{\mu } \int {\text {d}k_1 } \frac { \langle |\delta \hat {n}_{\mu }(k_x, -2K_0\sin \alpha _0)|^2 \rangle _T }{ | {K_{x\mu }}/{K_0} | W_{Y\mu } } , \\ \end{alignedat} \end{align}
\begin{align} \begin{alignedat}{2} &\frac {p_r}{P_{ant}} &&\approx \pi ^{\frac {3}{2}} K_0L \frac {e^4}{m_e^2 \epsilon _0^2 \Omega ^4} \sum _{\mu } \int {\text {d}k_1 } \frac { \langle |\delta \hat {n}_{\mu }(k_x, -2K_0\sin \alpha _0)|^2 \rangle _T }{ | {K_{x\mu }}/{K_0} | W_{Y\mu } } , \\ \end{alignedat} \end{align}
where we have used (B.25) to write the term
![]() $|g \text {d}K/\text {d}\tau |_\mu$
as a function of
$|g \text {d}K/\text {d}\tau |_\mu$
as a function of
![]() $K_{x\mu }$
. The dependence of
$K_{x\mu }$
. The dependence of
![]() $k_x$
on
$k_x$
on
![]() $k_1$
in (D.19) can be explained as follows. First,
$k_1$
in (D.19) can be explained as follows. First,
![]() $k_x$
is related to the location along the path
$k_x$
is related to the location along the path
![]() $l_\mu$
through the Bragg condition in Cartesian coordinates in (3.6). In turn,
$l_\mu$
through the Bragg condition in Cartesian coordinates in (3.6). In turn,
![]() $l_\mu$
is related to
$l_\mu$
is related to
![]() $k_1$
through the Bragg condition when expressed in beam-aligned coordinates,
$k_1$
through the Bragg condition when expressed in beam-aligned coordinates,
![]() $k_1 \approx - 2 K_\mu$
to lowest order, since the difference
$k_1 \approx - 2 K_\mu$
to lowest order, since the difference
![]() $l_\mu - l_\nu$
is of order
$l_\mu - l_\nu$
is of order
![]() $\sim W$
as we just saw.
$\sim W$
as we just saw.
Equation (D.19) recovers the same result as Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) when using
![]() $\langle |\delta \hat {n}_{b,\mu }|^2 \rangle _T$
. The one-dimensional change of variables between
$\langle |\delta \hat {n}_{b,\mu }|^2 \rangle _T$
. The one-dimensional change of variables between
![]() $k_x$
and
$k_x$
and
![]() $k_1$
shows that, to lowest order and at scales
$k_1$
shows that, to lowest order and at scales
![]() $\sim 1/\lambda$
, the density-fluctuation spectra in Cartesian coordinates is related to the beam-aligned spectrum of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) by a rotation of angle
$\sim 1/\lambda$
, the density-fluctuation spectra in Cartesian coordinates is related to the beam-aligned spectrum of Hall-Chen et al. (Reference Hall-Chen, Parra and Hillesheim2022
Reference Hall-Chen, Parra and Hillesheimb
) by a rotation of angle
![]() $\alpha _\mu$
, and we have
$\alpha _\mu$
, and we have
![]() $\langle |\delta \hat {n}_{\mu }(k_x, -2K_0\sin \alpha _0)|^2 \rangle _T = \langle |\delta \hat {n}_{b,\mu }( k_x \cos \alpha _\mu - 2K_0\sin \alpha _0 \sin \alpha _\mu , 0)|^2 \rangle _T$
. Noting that
$\langle |\delta \hat {n}_{\mu }(k_x, -2K_0\sin \alpha _0)|^2 \rangle _T = \langle |\delta \hat {n}_{b,\mu }( k_x \cos \alpha _\mu - 2K_0\sin \alpha _0 \sin \alpha _\mu , 0)|^2 \rangle _T$
. Noting that
![]() $k_x \cos \alpha _\mu - 2K_0\sin \alpha _0 \sin \alpha _\mu \approx -2 K_\mu \approx k_1$
by use of the Bragg conditions, we have therefore recovered the equivalence in the one-dimensional scattered power in both representations.
$k_x \cos \alpha _\mu - 2K_0\sin \alpha _0 \sin \alpha _\mu \approx -2 K_\mu \approx k_1$
by use of the Bragg conditions, we have therefore recovered the equivalence in the one-dimensional scattered power in both representations.