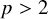1 Introduction
In [Reference Pappas and RapoportPR24], Pappas and Rapoport conjecture the existence of “canonical” integral models with parahoric level structure and establish this conjecture in most cases of Hodge type. In this work, we prove the conjecture of Pappas and Rapoport for (almost all) Shimura varieties of abelian type. In particular, we prove the following theorem.
Theorem A (See Theorem 4.10).
Let
![]() $p>2$
. Then the Pappas–Rapoport conjecture holds for Shimura varieties of abelian type with parahoric level structure at p.
$p>2$
. Then the Pappas–Rapoport conjecture holds for Shimura varieties of abelian type with parahoric level structure at p.
Let us begin to contextualize this result. Shimura varieties are algebro-geometric objects which sit at the intersection of number theory and representation theory. They take the form of a projective system
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
, where
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
, where
![]() $\mathbf {G}$
is a reductive group over
$\mathbf {G}$
is a reductive group over
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbf {X}$
is some auxiliary Hodge-theoretic datum, and
$\mathbf {X}$
is some auxiliary Hodge-theoretic datum, and
![]() $\mathsf {K} \subseteq \mathbf {G}(\mathbb {A}_f)$
ranges over (neat) compact open subgroups. Shimura varieties have been inextricably linked with the Langlands program from its inception, as the cohomology of
$\mathsf {K} \subseteq \mathbf {G}(\mathbb {A}_f)$
ranges over (neat) compact open subgroups. Shimura varieties have been inextricably linked with the Langlands program from its inception, as the cohomology of
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
ought to realize the global Langlands conjecture for
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
ought to realize the global Langlands conjecture for
![]() $\mathbf {G}$
(see e.g., [Reference KottwitzKot90]). Central to this cohomological understanding of the Langlands program is a conjecture which posits a “motivic decomposition” of the
$\mathbf {G}$
(see e.g., [Reference KottwitzKot90]). Central to this cohomological understanding of the Langlands program is a conjecture which posits a “motivic decomposition” of the
![]() $\bar {\mathbb {F}}_p$
-points of certain “canonical” integral models
$\bar {\mathbb {F}}_p$
-points of certain “canonical” integral models
![]() $\{\mathscr {S}_{\mathsf {K}}\}_{\mathsf {K}}$
of
$\{\mathscr {S}_{\mathsf {K}}\}_{\mathsf {K}}$
of
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
(see [Reference Langlands and RapoportLR87]). It is then not surprising that the construction of such natural integral models of Shimura varieties has prominently featured in many of the advances in the Langlands program.
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})\}_{\mathsf {K}}$
(see [Reference Langlands and RapoportLR87]). It is then not surprising that the construction of such natural integral models of Shimura varieties has prominently featured in many of the advances in the Langlands program.
Constructing such canonical integral models, and even characterizing what constitutes a “canonical” integral model, is quite difficult. Despite their importance, Shimura varieties in general remain fairly inexplicit in their definition. The variety
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})$
ought to parameterize
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G}, \mathbf {X})$
ought to parameterize
![]() $\mathbf {G}^c$
-motives M of type
$\mathbf {G}^c$
-motives M of type
![]() $\mathbf {X}$
with
$\mathbf {X}$
with
![]() $\mathsf {K}$
-level structure on the étale realization of M (e.g., see [Reference MilneMil13]). Here
$\mathsf {K}$
-level structure on the étale realization of M (e.g., see [Reference MilneMil13]). Here
![]() $\mathbf {G}^c$
is a certain quotient of
$\mathbf {G}^c$
is a certain quotient of
![]() $\mathbf {G}$
, which agrees with
$\mathbf {G}$
, which agrees with
![]() $\mathbf {G}$
in the Hodge-type case, but differs from
$\mathbf {G}$
in the Hodge-type case, but differs from
![]() $\mathbf {G}$
in some abelian-type cases. While technical in nature, consideration of
$\mathbf {G}$
in some abelian-type cases. While technical in nature, consideration of
![]() $\mathbf {G}^c$
is crucial for such a conjectural motivic interpretation. Unfortunately, such a motivic description is currently out of reach, and instead
$\mathbf {G}^c$
is crucial for such a conjectural motivic interpretation. Unfortunately, such a motivic description is currently out of reach, and instead
![]() $\textrm {Sh}_{\mathsf { K}}(\mathbf {G}, \mathbf {X})$
is constructed from various abstract algebro-geometric existence results, which are not amenable to the study of integral models.
$\textrm {Sh}_{\mathsf { K}}(\mathbf {G}, \mathbf {X})$
is constructed from various abstract algebro-geometric existence results, which are not amenable to the study of integral models.
Despite this, Pappas and Rapoport in [Reference Pappas and RapoportPR24] (building off previous work of Pappas in [Reference PappasPap22]) made significant headway in a definition of such conjectural canonical integral models when
![]() $\mathsf {K} = \mathsf {K}_p \mathsf {K}^p$
where
$\mathsf {K} = \mathsf {K}_p \mathsf {K}^p$
where
![]() $\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
is a parahoric subgroup of
$\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
is a parahoric subgroup of
![]() ${\mathbf {G}}(\mathbb {Q}_p)$
. This parahoricity-at-p condition may be thought of as representing the situation where relatively little level structure is imposed at p.
${\mathbf {G}}(\mathbb {Q}_p)$
. This parahoricity-at-p condition may be thought of as representing the situation where relatively little level structure is imposed at p.
To explicate their work, let E be the completion of the reflex field of
![]() $(\mathbf {G}, \mathbf {X})$
at a place v lying over p. Pappas and Rapoport call a system
$(\mathbf {G}, \mathbf {X})$
at a place v lying over p. Pappas and Rapoport call a system
![]() $\{ \mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
of
$\{ \mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
of
![]() $\mathcal{O}_E$
-models of
$\mathcal{O}_E$
-models of
![]() $\{\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G}, \mathbf {X})_E\}_{\mathsf { K}^p}$
canonical if
$\{\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G}, \mathbf {X})_E\}_{\mathsf { K}^p}$
canonical if
-
(i) the transition maps between the varying levels are finite étale,
-
(ii) if R is a characteristic
 $(0,p)$
discrete valuation ring over
$(0,p)$
discrete valuation ring over
 $\mathcal{O}_E$
then
$\mathcal{O}_E$
then 
-
(iii) there exists a
 $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
 $\mathscr {P}_{\mathsf {K}}$
on
$\mathscr {P}_{\mathsf {K}}$
on
 $\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
modeling the étale realization functor on
$\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
modeling the étale realization functor on
 $\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G}, \mathbf {X})_E$
,
$\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G}, \mathbf {X})_E$
, -
(iv) and for every
 $\bar {\mathbb {F}}_p$
-point x of
$\bar {\mathbb {F}}_p$
-point x of
 $\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})$
, there is an isomorphism (1.1)such that
$\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})$
, there is an isomorphism (1.1)such that
 $\Theta _x^\ast (\mathscr {P}_{\mathsf {K}}) = \mathscr {P}^{\textrm {univ}}$
.
$\Theta _x^\ast (\mathscr {P}_{\mathsf {K}}) = \mathscr {P}^{\textrm {univ}}$
.
Here the étale realization is a certain
![]() $\mathcal{G}^c(\mathbb {Z}_p)$
-local system on
$\mathcal{G}^c(\mathbb {Z}_p)$
-local system on
![]() $\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
which should be thought of as the étale realization of the “universal motive” on
$\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
which should be thought of as the étale realization of the “universal motive” on
![]() $\textrm {Sh}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})$
, but whose definition is unconditional on such a motivic interpretation. The group
$\textrm {Sh}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})$
, but whose definition is unconditional on such a motivic interpretation. The group
![]() $\mathcal{G}^c$
is a parahoric
$\mathcal{G}^c$
is a parahoric
![]() $\mathbb {Z}_p$
-model for
$\mathbb {Z}_p$
-model for
![]() $\mathbf {G}^c$
which is determined from
$\mathbf {G}^c$
which is determined from
![]() $\mathcal{G}$
using Bruhat–Tits theory. Furthermore, when we speak of shtukas here we mean in the sense of [Reference Pappas and RapoportPR24], and
$\mathcal{G}$
using Bruhat–Tits theory. Furthermore, when we speak of shtukas here we mean in the sense of [Reference Pappas and RapoportPR24], and
![]() $\mathscr {P}_{\mathsf {K}^p}$
modeling the étale realization is meant in terms of the construction in [Reference Pappas and RapoportPR24, §2.6]. Finally,
$\mathscr {P}_{\mathsf {K}^p}$
modeling the étale realization is meant in terms of the construction in [Reference Pappas and RapoportPR24, §2.6]. Finally, ![]() is the completion of the integral local Shimura variety in the sense of [Reference Scholze and WeinsteinSW20, Chapter 25] with its universal shtuka
is the completion of the integral local Shimura variety in the sense of [Reference Scholze and WeinsteinSW20, Chapter 25] with its universal shtuka
![]() $\mathscr {P}^{\textrm {univ}}$
. We refer the reader to §4.1 for the definition of
$\mathscr {P}^{\textrm {univ}}$
. We refer the reader to §4.1 for the definition of
![]() $b_x$
and
$b_x$
and
![]() $x_0$
, but mention that
$x_0$
, but mention that ![]() is the geometric conjugacy class of cocharacters of
is the geometric conjugacy class of cocharacters of
![]() $G^c$
induced by the Hodge cocharacter
$G^c$
induced by the Hodge cocharacter ![]() of G, where we are writing
of G, where we are writing
![]() $G=\mathbf {G}_{\mathbb {Q}_p}$
and
$G=\mathbf {G}_{\mathbb {Q}_p}$
and
![]() $G^c=\mathbf {G}^c_{\mathbb {Q}_p}$
.
$G^c=\mathbf {G}^c_{\mathbb {Q}_p}$
.
To help process this definition, note that, given the motivational moduli description of
![]() $\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
, it is reasonable to expect that
$\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
, it is reasonable to expect that
![]() $\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
should be a moduli space of
$\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
should be a moduli space of
![]() $\mathcal{G}^c$
-motives. One can view conditions (iii) and (iv) as saying that
$\mathcal{G}^c$
-motives. One can view conditions (iii) and (iv) as saying that
![]() $\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
possesses a shtuka, which should be the “shtuka realization” of the universal
$\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
possesses a shtuka, which should be the “shtuka realization” of the universal
![]() $\mathcal{G}^c$
-motive, which, while not provably universal, is universal everywhere formally locally. Furthermore, condition (i) is natural, and condition (ii) is a technical condition ensuring that the members of the system
$\mathcal{G}^c$
-motive, which, while not provably universal, is universal everywhere formally locally. Furthermore, condition (i) is natural, and condition (ii) is a technical condition ensuring that the members of the system
![]() $\{\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
have sufficiently large special fibers.
$\{\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
have sufficiently large special fibers.
Pappas and Rapoport prove that canonical integral models are unique if they exist, hence they do provide a good notion of models at parahoric level. Constructing such models is difficult though, and seems out of reach for general Shimura varieties with current methods. That said, when
![]() $(\mathbf {G},\mathbf {X})$
is of so-called “abelian type”, the situation is much improved. Shimura varieties of abelian type may be thought of intuitively as moduli spaces of abelian motives with extra structure, but this again is largely motivational (although see [Reference MilneMil13, Theorem 11.16] for a partial justification of this claim).
$(\mathbf {G},\mathbf {X})$
is of so-called “abelian type”, the situation is much improved. Shimura varieties of abelian type may be thought of intuitively as moduli spaces of abelian motives with extra structure, but this again is largely motivational (although see [Reference MilneMil13, Theorem 11.16] for a partial justification of this claim).
Building off the work of Kisin (and others), Kisin–Pappas [Reference Kisin and PappasKP18] and Kisin–Pappas–Zhou [Reference Kisin, Pappas and ZhouKPZ24] have constructed integral models for Shimura varieties of abelian type at parahoric level when p is an odd prime. These models have proven to be quite useful in applications (e.g., see [Reference Kisin and ZhouKZ21]), but they have not yet been well-studied. For instance, there is no a priori functoriality for these models, and it is not even clear that the models are independent of the various ancillary choices made in their construction. Our main theorem clarifies these points.
Theorem B (see Theorem 4.10).
Kisin–Pappas–Zhou models are canonical.
One of the most pleasing consequences of this result is the following.
Corollary C (See Corollary 4.12 and Theorem 4.14).
Kisin–Pappas–Zhou models are independent of all choices, and are functorial in the triple
![]() $(\mathbf {G}, \mathbf {X}, \mathcal{G})$
.
$(\mathbf {G}, \mathbf {X}, \mathcal{G})$
.
Beyond functoriality, our main result has several other applications to the integral geometry of Shimura varieties. For example, combining our work with the recent work of of Takaya [Reference TakayaTak24] gives a moduli-theoretic description of the Kisin–Pappas–Zhou models in the case where the given parahoric level
![]() $\mathsf {K}_p^{\prime } =\mathcal{G}'(\mathbb {Z}_p)$
is contained within a hyperspecial subgroup
$\mathsf {K}_p^{\prime } =\mathcal{G}'(\mathbb {Z}_p)$
is contained within a hyperspecial subgroup
![]() $\mathsf {K}_p$
of
$\mathsf {K}_p$
of
![]() $\mathbf {G}(\mathbb {Q}_p)$
and
$\mathbf {G}(\mathbb {Q}_p)$
and
![]() $(\mathbf {G},\mathbf {X})$
satisfies (SV5) (see [Reference MilneMil05, p. 311]). Indeed, by [Reference TakayaTak24, Theorem 3], the system
$(\mathbf {G},\mathbf {X})$
satisfies (SV5) (see [Reference MilneMil05, p. 311]). Indeed, by [Reference TakayaTak24, Theorem 3], the system
![]() $\{\mathscr {S}_{\mathsf {K}_p^{\prime }\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
parameterizing
$\{\mathscr {S}_{\mathsf {K}_p^{\prime }\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
parameterizing
![]() $\mathcal{G}'$
-level structures on the universal
$\mathcal{G}'$
-level structures on the universal
![]() $\mathcal{G}$
-shtuka over
$\mathcal{G}$
-shtuka over
![]() $\{\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is canonical, and therefore agrees with the system of Kisin–Pappas-Zhou models by Theorem B and the uniqueness of canonical models (see Proposition 4.4). In particular, the Kisin–Pappas-Zhou models themselves parameterize
$\{\mathscr {S}_{\mathsf { K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is canonical, and therefore agrees with the system of Kisin–Pappas-Zhou models by Theorem B and the uniqueness of canonical models (see Proposition 4.4). In particular, the Kisin–Pappas-Zhou models themselves parameterize
![]() $\mathcal{G}'$
-level structures.
$\mathcal{G}'$
-level structures.
In another direction, we expect our work will have applications to the theory of the Igusa stacks as developed in [Reference ZhangZha23] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a]. In [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a], it is shown that Kisin–Pappas–Zhou models of Hodge type admit a fiber product decomposition

at the level of v-sheaves. Here
![]() $\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})^\diamond $
denotes the v-sheaf associated to the p-adic completion of
$\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}(\mathbf {G},\mathbf {X})^\diamond $
denotes the v-sheaf associated to the p-adic completion of
![]() $\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
,
$\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
, ![]() is the moduli v-stack of
is the moduli v-stack of
![]() $\mathcal{G}$
-shtukas bounded by
$\mathcal{G}$
-shtukas bounded by ![]() ,
,
![]() $\textrm {Bun}_G$
is the stack of G-bundles on the Fargues-Fontaine curve, and
$\textrm {Bun}_G$
is the stack of G-bundles on the Fargues-Fontaine curve, and
![]() $\textrm {Igs}_{\mathsf {K}}$
is the Igusa stack defined in [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a]. This extends work of Zhang [Reference ZhangZha23] in the PEL-type case, and such a decomposition provides a crucial ingredient for the proof of torsion vanishing results for the cohomology of Shimura varieties, see [Reference Hamann and LeeHL23] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a]. Our results produce a map of v-sheaves
$\textrm {Igs}_{\mathsf {K}}$
is the Igusa stack defined in [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a]. This extends work of Zhang [Reference ZhangZha23] in the PEL-type case, and such a decomposition provides a crucial ingredient for the proof of torsion vanishing results for the cohomology of Shimura varieties, see [Reference Hamann and LeeHL23] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a]. Our results produce a map of v-sheaves ![]() for all Kisin–Pappas–Zhou models, and we expect that with this it will be possible to extend the results of [Reference ZhangZha23] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a] to the abelian-type case.
for all Kisin–Pappas–Zhou models, and we expect that with this it will be possible to extend the results of [Reference ZhangZha23] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24a] to the abelian-type case.
Let us close by mentioning a few ideas in the proof of Theorem 4.10. A useful guiding principle for Shimura data of abelian type is that they are “spanned” by two (largely orthogonal) extremes: Shimura data of Hodge type and Shimura data of toral type. However, it requires some care to put this idea into practice. The main ingredient in our proof is the development of a precise formalism for realizing this heuristic. We do this by extending ideas of Lovering (see [Reference LoveringLov17a]) from the setting of Kisin’s canonical integral models at hyperspecial level to the setting of arbitrary Kisin–Pappas–Zhou models. We are then able to prove Theorem A by reducing to the Hodge-type case (established in [Reference Pappas and RapoportPR24] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b], see Remark 4.7) and the toral-type case (established by the first-named author in [Reference DanielsDan25]). We expect these methods to have applications more generally.
Notation and conventions
-
⋄ For an S-scheme X, and a morphism of schemes
 $T\to S$
, we shorten the notation
$T\to S$
, we shorten the notation
 $X\times _S T$
to
$X\times _S T$
to
 $X_T$
. When
$X_T$
. When
 $T=\mathrm{Spec}\,(R)$
, we shorten this notation further to
$T=\mathrm{Spec}\,(R)$
, we shorten this notation further to
 $X_R$
. Similar conventions hold in other geometric categories.
$X_R$
. Similar conventions hold in other geometric categories. -
⋄ For a scheme X and subset S, we always consider the Zariski closure
 $\overline {S}$
as a reduced subscheme, unless stated otherwise.
$\overline {S}$
as a reduced subscheme, unless stated otherwise. -
⋄ Unless stated otherwise, we use the notation and terminology concerning v-sheaves, Fargues–Fontaine curve, and shtukas as in [Reference Pappas and RapoportPR24, §2]. In particular, when we speak of a shtuka over a
 $\mathbb {Z}_p$
-scheme X, we mean a shtuka over the v-sheaf
$\mathbb {Z}_p$
-scheme X, we mean a shtuka over the v-sheaf
 $X^{\lozenge /}$
in the sense of [Reference Pappas and RapoportPR24, Definition 2.3.2].
$X^{\lozenge /}$
in the sense of [Reference Pappas and RapoportPR24, Definition 2.3.2]. -
⋄ We use
 $\mathcal{G}\text {-}\mathbf {Sht}(\mathscr {X})$
and
$\mathcal{G}\text {-}\mathbf {Sht}(\mathscr {X})$
and  to denote the groupoid of
to denote the groupoid of
 $\mathcal{G}$
-shtukas on
$\mathcal{G}$
-shtukas on
 $\mathscr {X}$
and groupoid of
$\mathscr {X}$
and groupoid of
 $\mathcal{G}$
-shtukas bounded by
$\mathcal{G}$
-shtukas bounded by  on
on
 $\mathscr {X}$
, respectively.
$\mathscr {X}$
, respectively. -
⋄ A reductive group over a field F is always assumed connected.
2 Preliminaries
We begin by establishing some preliminaries which will be essential for the proofs of the main results. In particular, we review the Bruhat–Tits theory which is necessary for our purposes, and discuss torsors for fiber products of group schemes.
2.1 Some basic Bruhat–Tits theory
In this section we review some basic Bruhat–Tits theory. For more in-depth discussion in this direction we suggest the reader to consult [Reference Bruhat and TitsBT84] or [Reference Kaletha and PrasadKP23] and the references therein.
Throughout this section we fix a discretely valued field K with perfect residue field k. We denote by
![]() $K^{\textrm {ur}}$
the maximal unramified extension of K inside of
$K^{\textrm {ur}}$
the maximal unramified extension of K inside of
![]() $K^{\textrm {sep}}$
, and by
$K^{\textrm {sep}}$
, and by
![]() $\Gamma $
the Galois group
$\Gamma $
the Galois group
![]() $\text {Gal}(K^{\textrm {ur}}/K)$
. Denote by
$\text {Gal}(K^{\textrm {ur}}/K)$
. Denote by ![]() the inertia group of K.
the inertia group of K.
Remark 2.1. As
![]() $K^{\textrm {ur}}$
is another discretely valued field with perfect residue field, we will often apply to
$K^{\textrm {ur}}$
is another discretely valued field with perfect residue field, we will often apply to
![]() $K^{\textrm {ur}}$
without comment definitions which are initially stated for K.
$K^{\textrm {ur}}$
without comment definitions which are initially stated for K.
The building and its functorialities
Assume G is a reductive group over K. As in [Reference Kaletha and PrasadKP23, Definition 7.6.1] (cf. [Reference Kaletha and PrasadKP23, Definition 9.2.8]), associated to G is a building (in the sense of [Reference Kaletha and PrasadKP23, Definition 1.5.5])
where the right-hand side is as in [Reference Kaletha and PrasadKP23, Definition 7.6.1]. This building comes equipped with an action of
![]() $G({K^{\textrm {ur}}})\rtimes \Gamma $
. Moreover, the action of
$G({K^{\textrm {ur}}})\rtimes \Gamma $
. Moreover, the action of
![]() $G({K^{\textrm {ur}}})$
factors through the natural map
$G({K^{\textrm {ur}}})$
factors through the natural map
![]() $G({K^{\textrm {ur}}})\to G^{\text {ad}}({K^{\textrm {ur}}})$
.
$G({K^{\textrm {ur}}})\to G^{\text {ad}}({K^{\textrm {ur}}})$
.
Additionally, we have a building
which naturally comes equipped with an action of
![]() $G(K)$
which factorizes through the map
$G(K)$
which factorizes through the map
![]() $G(K)\to G^{\text {ad}}(K)$
. To distinguish these two objects, we call the
$G(K)\to G^{\text {ad}}(K)$
. To distinguish these two objects, we call the
![]() $\mathscr {B}(G,{K^{\textrm {ur}}})$
the building associated to G over
$\mathscr {B}(G,{K^{\textrm {ur}}})$
the building associated to G over
![]() ${K^{\textrm {ur}}}$
and
${K^{\textrm {ur}}}$
and
![]() $\mathscr {B}(G,K)$
the building associated to G over K.
$\mathscr {B}(G,K)$
the building associated to G over K.
Remark 2.2. The building(s) we are using here are more often called the reduced Bruhat–Tits building(s). While there exists a notion of the extended Bruhat– Tits building(s), we will not need these notions here and, in fact, this simpler object is better suited to our purposes. See [Reference Kaletha and PrasadKP23] for more details.
Various functorial properties for these buildings have been established in the literature, see [Reference LandvogtLan00] and [Reference Kaletha and PrasadKP23, §14]. However, in this article we require only two basic functoriality statements.
The first concerns quotient maps of reductive groups.
Lemma 2.3 (cf. [Reference Kaletha and PrasadKP23, Proposition 14.1.1]).
Suppose that
![]() $f\colon G\to H$
is a faithfully flat map of reductive groups over K. Then, there exists a unique surjective map
$f\colon G\to H$
is a faithfully flat map of reductive groups over K. Then, there exists a unique surjective map
which is equivariant for the map
![]() $G({K^{\textrm {ur}}})\rtimes \Gamma \to H({K^{\textrm {ur}}})\rtimes \Gamma $
. A similar statement holds for the buildings over K.
$G({K^{\textrm {ur}}})\rtimes \Gamma \to H({K^{\textrm {ur}}})\rtimes \Gamma $
. A similar statement holds for the buildings over K.
For the second statement, we first make the following definition. For a field F, a map
![]() ${f\colon G\to H}$
of reductive groups over F is an ad-isomorphism if
${f\colon G\to H}$
of reductive groups over F is an ad-isomorphism if
![]() $f(Z(G))\subseteq Z(H)$
, and the induced map
$f(Z(G))\subseteq Z(H)$
, and the induced map
![]() ${f^{\text {ad}}\colon G^{\text {ad}}\to H^{\text {ad}}}$
is an isomorphism. We record for later use the following proposition, whose proof is an exercise in assembling well-known facts about reductive groups over fields (e.g., see [Reference MilneMil17]).
${f^{\text {ad}}\colon G^{\text {ad}}\to H^{\text {ad}}}$
is an isomorphism. We record for later use the following proposition, whose proof is an exercise in assembling well-known facts about reductive groups over fields (e.g., see [Reference MilneMil17]).
Proposition 2.4. Let
![]() $f\colon G\to H$
be a map of reductive groups over F. Then, the following conditions on f are equivalent:
$f\colon G\to H$
be a map of reductive groups over F. Then, the following conditions on f are equivalent:
-
1. f is an ad-isomorphism,
-
2. the induced map
 $f\colon G^{\mathrm {der}}\to H^{\mathrm {der}}$
is a central isogeny.Footnote
1
$f\colon G^{\mathrm {der}}\to H^{\mathrm {der}}$
is a central isogeny.Footnote
1
The second basic functoriality result is the following.
Lemma 2.5. Suppose
![]() $f\colon G \to H$
is an ad-isomorphism of reductive groups over K. Then f induces a bijection of buildings
$f\colon G \to H$
is an ad-isomorphism of reductive groups over K. Then f induces a bijection of buildings
equivariant for the map
![]() $G({K^{\textrm {ur}}})\rtimes \Gamma \to H({K^{\textrm {ur}}})\rtimes \Gamma $
. Moreover, if
$G({K^{\textrm {ur}}})\rtimes \Gamma \to H({K^{\textrm {ur}}})\rtimes \Gamma $
. Moreover, if
![]() $g\colon H\to L$
is another ad-isomorphism, then
$g\colon H\to L$
is another ad-isomorphism, then
![]() $(g\circ f)_\ast =g_\ast \circ f_\ast $
. A similar statement holds for buildings over K.
$(g\circ f)_\ast =g_\ast \circ f_\ast $
. A similar statement holds for buildings over K.
Proof. As discussed on [Reference Kaletha and PrasadKP23, p. 264], there are natural
![]() $\Gamma $
-equivariant bijections
$\Gamma $
-equivariant bijections
which are equivariant for the maps
![]() $G({K^{\textrm {ur}}})\to G^{\text {ad}}({K^{\textrm {ur}}})$
and
$G({K^{\textrm {ur}}})\to G^{\text {ad}}({K^{\textrm {ur}}})$
and
![]() $H({K^{\textrm {ur}}})\to H^{\text {ad}}({K^{\textrm {ur}}})$
, respectively. These, together with the
$H({K^{\textrm {ur}}})\to H^{\text {ad}}({K^{\textrm {ur}}})$
, respectively. These, together with the
![]() $\Gamma $
-equivariant bijection
$\Gamma $
-equivariant bijection ![]() induced by
induced by
![]() $f^{\text {ad}}$
, gives us a
$f^{\text {ad}}$
, gives us a
![]() $\Gamma $
-equivariant bijection
$\Gamma $
-equivariant bijection
![]() $\mathscr {B}(G,{K^{\textrm {ur}}})\to \mathscr {B}(H,{K^{\textrm {ur}}})$
. That this is equivariant for the map
$\mathscr {B}(G,{K^{\textrm {ur}}})\to \mathscr {B}(H,{K^{\textrm {ur}}})$
. That this is equivariant for the map
![]() $G({K^{\textrm {ur}}})\to H({K^{\textrm {ur}}})$
is clear from construction as
$G({K^{\textrm {ur}}})\to H({K^{\textrm {ur}}})$
is clear from construction as
![]() $G({K^{\textrm {ur}}})$
and
$G({K^{\textrm {ur}}})$
and
![]() $H({K^{\textrm {ur}}})$
act through their images in
$H({K^{\textrm {ur}}})$
act through their images in
![]() $G^{\text {ad}}({K^{\textrm {ur}}})$
and
$G^{\text {ad}}({K^{\textrm {ur}}})$
and
![]() $H^{\text {ad}}({K^{\textrm {ur}}})$
, respectively. The proof for the buildings over K follows by passing to the fixed points for
$H^{\text {ad}}({K^{\textrm {ur}}})$
, respectively. The proof for the buildings over K follows by passing to the fixed points for
![]() $\Gamma $
.
$\Gamma $
.
Parahoric groups and group schemes
Let G be a reductive group over K. As in [Reference KottwitzKot97, §7] (see also [Reference Kaletha and PrasadKP23, §11.1]), one may construct a group homomorphism
where
![]() $\pi _1(G)$
denotes the fundamental group of Borovoi (see [Reference BorovoiBor98, §1]), a finitely generated abelian group, and the subscript
$\pi _1(G)$
denotes the fundamental group of Borovoi (see [Reference BorovoiBor98, §1]), a finitely generated abelian group, and the subscript
![]() $(-)_I$
denotes I-coinvariants. We call
$(-)_I$
denotes I-coinvariants. We call
![]() $\kappa _G$
the Kottwitz homomorphism associated to G. We let
$\kappa _G$
the Kottwitz homomorphism associated to G. We let
![]() $\kappa _G\otimes 1$
denote the composition of
$\kappa _G\otimes 1$
denote the composition of
![]() $\kappa _G$
with the map
$\kappa _G$
with the map
![]() $\pi _1(G)_I\to \pi _1(G)_I\otimes _{\mathbb {Z}}\mathbb {Q}$
.
$\pi _1(G)_I\to \pi _1(G)_I\otimes _{\mathbb {Z}}\mathbb {Q}$
.
We denote the kernel of
![]() $\kappa _G$
and
$\kappa _G$
and
![]() $\kappa _G\otimes 1$
by
$\kappa _G\otimes 1$
by
![]() $G({K^{\textrm {ur}}})^0$
and
$G({K^{\textrm {ur}}})^0$
and
![]() $G(K^{\textrm {ur}})^1$
, respectively.Footnote
2
The Kottwitz homomorphism is functorial in G, and thus the same holds for the subgroups
$G(K^{\textrm {ur}})^1$
, respectively.Footnote
2
The Kottwitz homomorphism is functorial in G, and thus the same holds for the subgroups
![]() $G({K^{\textrm {ur}}})^0$
and
$G({K^{\textrm {ur}}})^0$
and
![]() $G(K^{\textrm {ur}})^1$
. More precisely, if
$G(K^{\textrm {ur}})^1$
. More precisely, if
![]() $f\colon G\to H$
is a map of reductive groups over K, then the diagram
$f\colon G\to H$
is a map of reductive groups over K, then the diagram

commutes.
We then have the following definition of a parahoric group scheme.
Definition 2.6. A group
![]() $\mathcal{O}_K$
-scheme
$\mathcal{O}_K$
-scheme
![]() $\mathcal{G}$
is parahoric if:
$\mathcal{G}$
is parahoric if:
-
1.
 is a reductive group over K,
is a reductive group over K, -
2.
 $\mathcal{G}$
is a smooth affine group
$\mathcal{G}$
is a smooth affine group
 $\mathcal{O}_K$
-scheme with connected fibers,
$\mathcal{O}_K$
-scheme with connected fibers, -
3. there exists a point x in
 $\mathscr {B}(G,K)$
such that (2.1)
$\mathscr {B}(G,K)$
such that (2.1) $$ \begin{align} \mathcal{G}(\mathcal{O}_{K^{\textrm{ur}}}) = G(K^{\textrm{ur}})^0 \cap \textrm{Stab}_{G(K^{\textrm{ur}})}(x). \end{align} $$
$$ \begin{align} \mathcal{G}(\mathcal{O}_{K^{\textrm{ur}}}) = G(K^{\textrm{ur}})^0 \cap \textrm{Stab}_{G(K^{\textrm{ur}})}(x). \end{align} $$
Remark 2.7. That this definition of parahoric group scheme agrees with that originally defined in [Reference Bruhat and TitsBT84] is (essentially) the content of [Reference Haines and RapoportHR08, Proposition 3].
As in [Reference Kisin and PappasKP18, §9.2.6], associated to any point x of
![]() $\mathscr {B}(G,K)$
is a parahoric group scheme denoted by
$\mathscr {B}(G,K)$
is a parahoric group scheme denoted by
![]() $\mathcal{G}^\circ _x$
, characterized by Equation (2.1). Moreover, every parahoric group scheme arises in this way. A subgroup of
$\mathcal{G}^\circ _x$
, characterized by Equation (2.1). Moreover, every parahoric group scheme arises in this way. A subgroup of
![]() $G(K)$
is called parahoric if it is of the form
$G(K)$
is called parahoric if it is of the form
![]() $\mathcal{G}(\mathcal{O}_K)$
for a parahoric group
$\mathcal{G}(\mathcal{O}_K)$
for a parahoric group
![]() $\mathcal{O}_K$
-scheme
$\mathcal{O}_K$
-scheme
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
Parahoric models of tori and R-smooth tori
Suppose that T is a a torus over K. By Lemma 2.5 it’s clear that
![]() $\mathscr {B}(T,K)$
is a singleton, and thus that T has a unique parahoric model which we denote by
$\mathscr {B}(T,K)$
is a singleton, and thus that T has a unique parahoric model which we denote by
![]() $\mathcal{T}$
. As
$\mathcal{T}$
. As
![]() $\mathscr {B}(T,K)$
is a singleton,
$\mathscr {B}(T,K)$
is a singleton,
![]() $\mathcal{T}(\mathcal{O}_K)$
is equal
$\mathcal{T}(\mathcal{O}_K)$
is equal
![]() $T(K)^0$
.
$T(K)^0$
.
Let
![]() $\mathcal{T}^{\textrm {lft}}$
be the Néron model of T (e.g., see [Reference Kaletha and PrasadKP23, §B.7–B.8] and [Reference Bosch, Lütkebohmert and RaynaudBLR90]).
$\mathcal{T}^{\textrm {lft}}$
be the Néron model of T (e.g., see [Reference Kaletha and PrasadKP23, §B.7–B.8] and [Reference Bosch, Lütkebohmert and RaynaudBLR90]).
Proposition 2.8 (see [Reference Kaletha and PrasadKP23, §B.7–B.8]).
There is a functorial identification
![]() $\mathcal{T} \simeq (\mathcal{T}^{\textrm {lft}})^\circ $
.
$\mathcal{T} \simeq (\mathcal{T}^{\textrm {lft}})^\circ $
.
Fix a finite Galois extension
![]() $K_1$
of K splitting T, and set
$K_1$
of K splitting T, and set
![]() $T_1=\textrm {Res}_{K_1/K}T_{K_1}$
which admits a natural embedding
$T_1=\textrm {Res}_{K_1/K}T_{K_1}$
which admits a natural embedding
![]() $T\to T_1$
.
$T\to T_1$
.
Definition 2.9 ([Reference Kisin and ZhouKZ21, Definition 2.4.3]).
The torus T is called R-smooth if its Zariski closure in
![]() $\mathcal{T}_1^{\textrm {lft}}$
is a smooth group
$\mathcal{T}_1^{\textrm {lft}}$
is a smooth group
![]() $\mathcal{O}_K$
-scheme.Footnote
3
$\mathcal{O}_K$
-scheme.Footnote
3
Consider now a reductive group G over K. As
![]() $G_{K^{\textrm {ur}}}$
is quasi-split by Steinberg’s theorem (see [Reference SteinbergSte65, Theorem 1.9]), there is a unique
$G_{K^{\textrm {ur}}}$
is quasi-split by Steinberg’s theorem (see [Reference SteinbergSte65, Theorem 1.9]), there is a unique
![]() $G(K^{\textrm {ur}})$
-conjugacy class of maximally split maximal tori in
$G(K^{\textrm {ur}})$
-conjugacy class of maximally split maximal tori in
![]() $G_{K^{\textrm {ur}}}$
which are precisely the centralizers of maximal split tori (see [Reference BorelBor91, §20]).
$G_{K^{\textrm {ur}}}$
which are precisely the centralizers of maximal split tori (see [Reference BorelBor91, §20]).
Definition 2.10. We say that a reductive K-group G is R-smooth if one (equivalently any) maximally split maximal torus of
![]() $G_{K^{\textrm {ur}}}$
is R-smooth.
$G_{K^{\textrm {ur}}}$
is R-smooth.
As the formation of Néron models commutes with unramified base change, Definition 2.10 agrees with that of Definition 2.9 when G is a torus.
Abelianization of parahoric group schemes
Suppose that G is a reductive group over
![]() $\mathcal{O}_K$
, and consider the short exact sequence of reductive groups
$\mathcal{O}_K$
, and consider the short exact sequence of reductive groups
By Lemma 2.3 and Lemma 2.5 we obtain maps of buildings
where the first map is a bijection and the second is surjective, and the maps are equivariant for
![]() $G^{\mathrm {der}}(K)\to G(K)$
and
$G^{\mathrm {der}}(K)\to G(K)$
and
![]() $G(K)\to G^{\text {ab}}(K)$
, respectively. Similar statements hold for the buildings over
$G(K)\to G^{\text {ab}}(K)$
, respectively. Similar statements hold for the buildings over
![]() ${K^{\textrm {ur}}}$
.
${K^{\textrm {ur}}}$
.
Let us fix a point y of
![]() $\mathscr {B}(G,K)$
and set
$\mathscr {B}(G,K)$
and set
![]() $x=i_\ast ^{-1}(y)$
and
$x=i_\ast ^{-1}(y)$
and
![]() $z=f_\ast (y)$
. By the functoriality of the Kottwitz homomorphism and the equivariant properties of these maps, we see by [Reference Kaletha and PrasadKP23, Corollary 2.10.10] that i and f extend to maps
$z=f_\ast (y)$
. By the functoriality of the Kottwitz homomorphism and the equivariant properties of these maps, we see by [Reference Kaletha and PrasadKP23, Corollary 2.10.10] that i and f extend to maps
![]() $i\colon \mathcal{G}_x\to \mathcal{G}_y$
and
$i\colon \mathcal{G}_x\to \mathcal{G}_y$
and
![]() $f\colon \mathcal{G}_y\to \mathcal{G}_z$
, restricting to maps
$f\colon \mathcal{G}_y\to \mathcal{G}_z$
, restricting to maps
![]() $i\colon \mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
and
$i\colon \mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
and
![]() $f\colon \mathcal{G}_y^\circ \to \mathcal{G}_z^\circ $
.
$f\colon \mathcal{G}_y^\circ \to \mathcal{G}_z^\circ $
.
Proposition 2.11. If
![]() $G^{\mathrm {der}}$
is R-smooth and the map
$G^{\mathrm {der}}$
is R-smooth and the map
![]() $\pi _1(G^{\mathrm {der}})_I\to \pi _1(G)_I$
is injective, then we have a short exact sequence
$\pi _1(G^{\mathrm {der}})_I\to \pi _1(G)_I$
is injective, then we have a short exact sequence
Proof. First observe that by the setup, we have a diagram
We first claim that
![]() $\mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective. Let T be a maximally split maximal torus in
$\mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective. Let T be a maximally split maximal torus in
![]() $G_{K^{\textrm {ur}}}$
as in [Reference Kaletha and PrasadKP23, §8.3.6]. Then as in loc. cit. there exists a map
$G_{K^{\textrm {ur}}}$
as in [Reference Kaletha and PrasadKP23, §8.3.6]. Then as in loc. cit. there exists a map
![]() $\mathcal{T}(\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
, thus it suffices to show that
$\mathcal{T}(\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
, thus it suffices to show that
![]() $\mathcal{T}(\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective. That said, observe that
$\mathcal{T}(\mathcal{O}_{K^{\textrm {ur}}}) \to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective. That said, observe that
![]() $\ker (T \to G^{\text {ab}}) = T\cap G^{\mathrm {der}}$
is a torus and therefore, by [Reference Kaletha and PrasadKP23, Lemma 2.5.20] the map
$\ker (T \to G^{\text {ab}}) = T\cap G^{\mathrm {der}}$
is a torus and therefore, by [Reference Kaletha and PrasadKP23, Lemma 2.5.20] the map
![]() $T(K^{\textrm {ur}})^0 \to G^{\text {ab}}(K^{\textrm {ur}})^0$
is surjective, so the claim follows.
$T(K^{\textrm {ur}})^0 \to G^{\text {ab}}(K^{\textrm {ur}})^0$
is surjective, so the claim follows.
We now prove that
![]() $f\colon \mathcal{G}_y^\circ \to \mathcal{G}_z^\circ $
is faithfully flat. To see that f is surjective, we observe that f is surjective over K, being the map
$f\colon \mathcal{G}_y^\circ \to \mathcal{G}_z^\circ $
is faithfully flat. To see that f is surjective, we observe that f is surjective over K, being the map
![]() $G\to G^{\text {ab}}$
. Thus, it suffices to show that
$G\to G^{\text {ab}}$
. Thus, it suffices to show that
![]() $f_{k^{\textrm {sep}}}$
contains every point of
$f_{k^{\textrm {sep}}}$
contains every point of
![]() $\mathcal{G}_z^\circ (k^{\textrm {sep}})$
in its image. As
$\mathcal{G}_z^\circ (k^{\textrm {sep}})$
in its image. As
![]() $\mathcal{G}_z^\circ $
is smooth, we know that
$\mathcal{G}_z^\circ $
is smooth, we know that
![]() $\mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})\to \mathcal{G}_z^\circ (k^{\textrm {sep}})$
is surjective (e.g., see [Reference GrothendieckGro67, Thèoréme 18.5.17]), and, since
$\mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})\to \mathcal{G}_z^\circ (k^{\textrm {sep}})$
is surjective (e.g., see [Reference GrothendieckGro67, Thèoréme 18.5.17]), and, since
![]() $\mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}})\to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective, the claim follows. To show that f is flat, we may, by the critére de platitude par fibres (see [Reference GrothendieckGro66, Thèoréme 11.3.10]), show instead that
$\mathcal{G}_y^\circ (\mathcal{O}_{K^{\textrm {ur}}})\to \mathcal{G}_z^\circ (\mathcal{O}_{K^{\textrm {ur}}})$
is surjective, the claim follows. To show that f is flat, we may, by the critére de platitude par fibres (see [Reference GrothendieckGro66, Thèoréme 11.3.10]), show instead that
![]() $f_K$
and
$f_K$
and
![]() $f_k$
are flat. To show that
$f_k$
are flat. To show that
![]() $f_k$
is flat, we observe that by [Reference MilneMil17, Theorem 3.34]
$f_k$
is flat, we observe that by [Reference MilneMil17, Theorem 3.34]
![]() $f_k$
factorizes as a faithfully flat map g followed by a closed immersion i. But, as
$f_k$
factorizes as a faithfully flat map g followed by a closed immersion i. But, as
![]() $f_k$
is surjective, i must be a homeomorphism on the underlying space which, as
$f_k$
is surjective, i must be a homeomorphism on the underlying space which, as
![]() $(\mathcal{G}_z^\circ )_k$
is reduced, must be the entire space. Thus,
$(\mathcal{G}_z^\circ )_k$
is reduced, must be the entire space. Thus,
![]() $f_k=g$
is flat. A similar argument holds for
$f_k=g$
is flat. A similar argument holds for
![]() $f_K$
.
$f_K$
.
Finally, since
![]() $G^{\mathrm {der}}$
is R-smooth, it follows from [Reference Kisin and ZhouKZ21, Proposition 2.4.8] that the map
$G^{\mathrm {der}}$
is R-smooth, it follows from [Reference Kisin and ZhouKZ21, Proposition 2.4.8] that the map
![]() $\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion. Next observe that by the injectivity of
$\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion. Next observe that by the injectivity of
![]() $\pi _1(G^{\mathrm {der}})_I\to \pi _1(G)_I$
, one may conclude that
$\pi _1(G^{\mathrm {der}})_I\to \pi _1(G)_I$
, one may conclude that
![]() $G^{\mathrm {der}}(K^{\textrm {ur}})^0=G^{\mathrm {der}}(K^{\textrm {ur}})\cap G(K^{\textrm {ur}})^0$
. Using this, and the fact that the map
$G^{\mathrm {der}}(K^{\textrm {ur}})^0=G^{\mathrm {der}}(K^{\textrm {ur}})\cap G(K^{\textrm {ur}})^0$
. Using this, and the fact that the map
![]() $\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion, one may check that
$\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion, one may check that
![]() $\mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
is a closed immersion. Indeed, since
$\mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
is a closed immersion. Indeed, since
![]() $\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion and
$\mathcal{G}_x\to \mathcal{G}_y$
is a closed immersion and
![]() $\mathcal{G}_y^\circ $
is an open group subscheme of
$\mathcal{G}_y^\circ $
is an open group subscheme of
![]() $\mathcal{G}_y$
,
$\mathcal{G}_y$
,
![]() $\mathcal{G}_x\cap \mathcal{G}_y^\circ $
is an open group subscheme of
$\mathcal{G}_x\cap \mathcal{G}_y^\circ $
is an open group subscheme of
![]() $\mathcal{G}_x$
(and thus smooth) and a closed subgroup scheme of
$\mathcal{G}_x$
(and thus smooth) and a closed subgroup scheme of
![]() $\mathcal{G}_y^\circ $
. We will be done if we can show that
$\mathcal{G}_y^\circ $
. We will be done if we can show that
![]() $\mathcal{G}_x\cap \mathcal{G}_y^\circ $
and
$\mathcal{G}_x\cap \mathcal{G}_y^\circ $
and
![]() $\mathcal{G}_x^\circ $
are equal. By [Reference Kaletha and PrasadKP23, Corollary 2.10.11] it suffices to check the two have the same
$\mathcal{G}_x^\circ $
are equal. By [Reference Kaletha and PrasadKP23, Corollary 2.10.11] it suffices to check the two have the same
![]() $\mathcal{O}_{K^{\textrm {ur}}}$
-points, and this follows from the equality
$\mathcal{O}_{K^{\textrm {ur}}}$
-points, and this follows from the equality
![]() $G^{\mathrm {der}}(K^{\textrm {ur}})^0=G^{\mathrm {der}}(K^{\textrm {ur}})\cap G(K^{\textrm {ur}})^0$
. Finally to show that the closed immersion
$G^{\mathrm {der}}(K^{\textrm {ur}})^0=G^{\mathrm {der}}(K^{\textrm {ur}})\cap G(K^{\textrm {ur}})^0$
. Finally to show that the closed immersion
![]() $\mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
identifies
$\mathcal{G}_x^\circ \to \mathcal{G}_y^\circ $
identifies
![]() $\mathcal{G}_x^\circ $
with
$\mathcal{G}_x^\circ $
with
![]() $\ker (\mathcal{G}_y^\circ \to \mathcal{G}_z^\circ )$
it suffices to check this claim on the generic fiber,Footnote
4
where it is clear.
$\ker (\mathcal{G}_y^\circ \to \mathcal{G}_z^\circ )$
it suffices to check this claim on the generic fiber,Footnote
4
where it is clear.
In practice, if we have fixed a parahoric model
![]() $\mathcal{G}$
of G, then we write the unique parahoric model of
$\mathcal{G}$
of G, then we write the unique parahoric model of
![]() $G^{\text {ab}}$
by
$G^{\text {ab}}$
by
![]() $\mathcal{G}^{\text {ab}}$
. Given Proposition 2.11 this notational abuse is not too severe. Similarly, we denote the associated parahoric model of
$\mathcal{G}^{\text {ab}}$
. Given Proposition 2.11 this notational abuse is not too severe. Similarly, we denote the associated parahoric model of
![]() $G^{\textrm {der}}$
by
$G^{\textrm {der}}$
by
![]() $\mathcal{G}^{\textrm {der}}$
.
$\mathcal{G}^{\textrm {der}}$
.
Parahoric group schemes and central quotients
Let
![]() $f\colon G\to G'$
be a faithfully flat map such that
$f\colon G\to G'$
be a faithfully flat map such that ![]() is a torus over K. Let x be a point of
is a torus over K. Let x be a point of
![]() $\mathscr {B}(G,K)$
and
$\mathscr {B}(G,K)$
and
![]() $x'$
its image under the map the map
$x'$
its image under the map the map
![]() $f_\ast $
from Lemma 2.3. Let us write
$f_\ast $
from Lemma 2.3. Let us write
![]() $\mathcal{G}=\mathcal{G}_x^\circ $
and
$\mathcal{G}=\mathcal{G}_x^\circ $
and
![]() $\mathcal{G}'=\mathcal{G}_{x'}^\circ $
$\mathcal{G}'=\mathcal{G}_{x'}^\circ $
As
![]() $f_\ast $
is equivariant for the map
$f_\ast $
is equivariant for the map
![]() $G({K^{\textrm {ur}}})\to G'({K^{\textrm {ur}}})$
and the Kottwitz homomorphism is functorial, we deduce that f maps
$G({K^{\textrm {ur}}})\to G'({K^{\textrm {ur}}})$
and the Kottwitz homomorphism is functorial, we deduce that f maps
![]() $\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})$
into
$\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})$
into
![]() $\mathcal{G}'(\mathcal{O}_{K^{\textrm {ur}}})$
. Thus, by [Reference Kaletha and PrasadKP23, Corollary 2.10.10] f uniquely lifts to a map
$\mathcal{G}'(\mathcal{O}_{K^{\textrm {ur}}})$
. Thus, by [Reference Kaletha and PrasadKP23, Corollary 2.10.10] f uniquely lifts to a map
![]() $\mathcal{G}\to \mathcal{G}'$
. When Z is R-smooth, one can say more.
$\mathcal{G}\to \mathcal{G}'$
. When Z is R-smooth, one can say more.
Proposition 2.12 ([Reference Kisin and ZhouKZ21, Proposition 2.4.13]).
Suppose that Z is an R-smooth torus. Then, there exists a short exact sequence of group
![]() $\mathcal{O}_K$
-schemes
$\mathcal{O}_K$
-schemes
where
![]() $\mathcal{Z}$
is the Zariski closure of Z in
$\mathcal{Z}$
is the Zariski closure of Z in
![]() $\mathcal{G}$
. Moreover,
$\mathcal{G}$
. Moreover,
![]() $\mathcal{Z}$
is a smooth group
$\mathcal{Z}$
is a smooth group
![]() $\mathcal{O}_K$
-scheme.
$\mathcal{O}_K$
-scheme.
Parahoric group schemes and ad-isomorphisms
Suppose that
![]() $i\colon G\to H$
is an injective ad-isomorphism of reductive groups over K. Suppose that
$i\colon G\to H$
is an injective ad-isomorphism of reductive groups over K. Suppose that
![]() $\mathcal{H}$
is a parahoric model of H, and y is a point of
$\mathcal{H}$
is a parahoric model of H, and y is a point of
![]() $\mathscr {B}(H,K)$
such that
$\mathscr {B}(H,K)$
such that
![]() $\mathcal{H}$
is isomorphic to
$\mathcal{H}$
is isomorphic to
![]() $\mathcal{H}_y^\circ $
. By Lemma 2.5 there is a unique point x of
$\mathcal{H}_y^\circ $
. By Lemma 2.5 there is a unique point x of
![]() $\mathscr {B}(G,K)$
such that
$\mathscr {B}(G,K)$
such that
![]() $y=i_\ast (x)$
.
$y=i_\ast (x)$
.
The following basic proposition provides a recognition principle for
![]() $\mathcal{G}_x^\circ $
.
$\mathcal{G}_x^\circ $
.
Proposition 2.13. A model
![]() $\mathcal{G}$
of G is isomorphic to
$\mathcal{G}$
of G is isomorphic to
![]() $\mathcal{G}_x^\circ $
if it is a smooth affine group
$\mathcal{G}_x^\circ $
if it is a smooth affine group
![]() $\mathcal{O}_K$
-scheme with connected fibers and
$\mathcal{O}_K$
-scheme with connected fibers and
Moreover, i extends to a map of
![]() $\mathcal{O}_K$
-group schemes
$\mathcal{O}_K$
-group schemes
![]() $\mathcal{G} \to \mathcal{H}$
.
$\mathcal{G} \to \mathcal{H}$
.
Proof. By the definition of parahoric group schemes, and the definition of
![]() $\mathcal{G}_x^\circ $
, it suffices to show that
$\mathcal{G}_x^\circ $
, it suffices to show that
Since
![]() $i_\ast $
defines a bijection
$i_\ast $
defines a bijection ![]() which is equivariant for the map
which is equivariant for the map
![]() $G({K^{\textrm {ur}}}) \to H({K^{\textrm {ur}}})$
, we deduce that
$G({K^{\textrm {ur}}}) \to H({K^{\textrm {ur}}})$
, we deduce that
The inclusion
![]() $\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}}) \subseteq \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
then follows immediately from (2.2). Additionally, as
$\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}}) \subseteq \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
then follows immediately from (2.2). Additionally, as
![]() $\mathcal{G}$
is a smooth affine group
$\mathcal{G}$
is a smooth affine group
![]() $\mathcal{O}_K$
-scheme with connected fibers, it follows from [Reference Kaletha and PrasadKP23, Proposition 8.3.15] that
$\mathcal{O}_K$
-scheme with connected fibers, it follows from [Reference Kaletha and PrasadKP23, Proposition 8.3.15] that
![]() $\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}}) \subseteq G({K^{\textrm {ur}}})^0$
. Thus,
$\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}}) \subseteq G({K^{\textrm {ur}}})^0$
. Thus,
![]() $\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})\subseteq G({K^{\textrm {ur}}})^0\cap \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
.
$\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})\subseteq G({K^{\textrm {ur}}})^0\cap \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
.
On the other hand, if g belongs to
![]() $G({K^{\textrm {ur}}})^0 \cap \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
, then
$G({K^{\textrm {ur}}})^0 \cap \textrm {Stab}_{G({K^{\textrm {ur}}})}(x)$
, then
![]() $i(g)$
belongs to
$i(g)$
belongs to
![]() $\mathcal{H}(\mathcal{O}_{K^{\textrm {ur}}})$
by functoriality of the Kottwitz homomorphism along with the identity (2.4). Hence (2.2) implies that g belongs to
$\mathcal{H}(\mathcal{O}_{K^{\textrm {ur}}})$
by functoriality of the Kottwitz homomorphism along with the identity (2.4). Hence (2.2) implies that g belongs to
![]() $\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})$
.
$\mathcal{G}(\mathcal{O}_{K^{\textrm {ur}}})$
.
Finally, the fact that i extends to a morphism
![]() $i\colon \mathcal{G}\to \mathcal{H}$
follows from [Reference Kaletha and PrasadKP23, Corollary 2.10.10] by (2.2).
$i\colon \mathcal{G}\to \mathcal{H}$
follows from [Reference Kaletha and PrasadKP23, Corollary 2.10.10] by (2.2).
2.2 Fiber products of groups
In this subsection we aim to collect some facts concerning fiber products of groups, in various contexts, that will be useful below.
Smoothness and connectedness of fiber products of group schemes
Fix a connected scheme S and consider a Cartesian diagram of group S-schemes

Set
![]() $\mathcal{K}$
to be the group S-scheme
$\mathcal{K}$
to be the group S-scheme
![]() $\ker (f)$
.
$\ker (f)$
.
Proposition 2.14. Suppose that f is faithfully flat and quasi-compact, and that
![]() $\mathcal{K}$
and
$\mathcal{K}$
and
![]() $\mathcal{C}$
are smooth group S-schemes with connected fibers. Then,
$\mathcal{C}$
are smooth group S-schemes with connected fibers. Then,
![]() $\mathcal{D}$
is a smooth group S-scheme with connected fibers.
$\mathcal{D}$
is a smooth group S-scheme with connected fibers.
One may replace all instances of “connected” in the assumptions and conclusion of the above statement by “geometrically connected”, “irreducible”, or “geometrically irreducible” by standard theory concerning algebraic groups (see [Reference MilneMil17, Summary 1.36]). We use this observation freely below.
Proof of Proposition 2.14.
The morphism
![]() $\mathcal{A}\times _{\mathcal{B}}\mathcal{A}\to \mathcal{K}\times _S \mathcal{A}$
given by
$\mathcal{A}\times _{\mathcal{B}}\mathcal{A}\to \mathcal{K}\times _S \mathcal{A}$
given by
![]() $(g,h)\mapsto (gh^{-1},h)$
is an isomorphism. But, as
$(g,h)\mapsto (gh^{-1},h)$
is an isomorphism. But, as
![]() $\mathcal{K}\to S$
is smooth, thus so is
$\mathcal{K}\to S$
is smooth, thus so is
![]() $\mathcal{K}\times _S \mathcal{A}\to \mathcal{A}$
, and thus so is
$\mathcal{K}\times _S \mathcal{A}\to \mathcal{A}$
, and thus so is
![]() $\mathcal{A}\times _{\mathcal{B}}\mathcal{A}\to \mathcal{A}$
. As f is faitfully flat and quasi-compact, we deduce by fpqc descent for smoothness (e.g., see [SP17, Tag 0429]) that f is smooth. By stability of smoothness under base change we deduce that
$\mathcal{A}\times _{\mathcal{B}}\mathcal{A}\to \mathcal{A}$
. As f is faitfully flat and quasi-compact, we deduce by fpqc descent for smoothness (e.g., see [SP17, Tag 0429]) that f is smooth. By stability of smoothness under base change we deduce that
![]() $q\colon \mathcal{D}\to \mathcal{C}$
is smooth, and as
$q\colon \mathcal{D}\to \mathcal{C}$
is smooth, and as
![]() $\mathcal{C}\to S$
is smooth thus so is the composition
$\mathcal{C}\to S$
is smooth thus so is the composition
![]() $\mathcal{D}\to S$
.
$\mathcal{D}\to S$
.
To prove that
![]() $\mathcal{D}\to S$
has connected fibers, let s be an element of S and consider the map
$\mathcal{D}\to S$
has connected fibers, let s be an element of S and consider the map
![]() $q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
. By assumption we have that
$q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
. By assumption we have that
![]() $\mathcal{C}_s$
is connected and
$\mathcal{C}_s$
is connected and
![]() $q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
is surjective. Moreover, by the argument in the previous paragraph we have that
$q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
is surjective. Moreover, by the argument in the previous paragraph we have that
![]() $q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
is smooth, and thus open. On the other hand, as
$q_s\colon \mathcal{D}_s\to \mathcal{C}_s$
is smooth, and thus open. On the other hand, as
![]() $\mathcal{K}\to S$
has geometrically connected fibers, the same holds true for f as these fibers are translations of geometric fibers of
$\mathcal{K}\to S$
has geometrically connected fibers, the same holds true for f as these fibers are translations of geometric fibers of
![]() $\mathcal{K}\to S$
. Thus, the map
$\mathcal{K}\to S$
. Thus, the map
![]() $q_s$
has geometrically connected fibers (see [SP17, Tag 055E]). Therefore we deduce that
$q_s$
has geometrically connected fibers (see [SP17, Tag 055E]). Therefore we deduce that
![]() $\mathcal{D}_s$
is connected as desired from the simple fact that if
$\mathcal{D}_s$
is connected as desired from the simple fact that if
![]() $f\colon Y\to X$
be an open surjective map of topological spaces with connected fibers and X is connected, then Y is connected.
$f\colon Y\to X$
be an open surjective map of topological spaces with connected fibers and X is connected, then Y is connected.
Some fiber products of parahoric group schemes
Suppose now that, as in §2.1, K is a discretely valued field with perfect residue field. Suppose further that we have a Cartesian diagram of group
![]() $\mathcal{O}_K$
-schemes
$\mathcal{O}_K$
-schemes

where
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\mathcal{B}$
, and
$\mathcal{B}$
, and
![]() $\mathcal{C}$
are parahoric group
$\mathcal{C}$
are parahoric group
![]() $\mathcal{O}_K$
-schemes. For simplicity we denote the generic fiber of
$\mathcal{O}_K$
-schemes. For simplicity we denote the generic fiber of
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\mathcal{B}$
,
$\mathcal{B}$
,
![]() $\mathcal{C}$
, and
$\mathcal{C}$
, and
![]() $\mathcal{D}$
, by
$\mathcal{D}$
, by
![]() $A,B,C,$
and D, respectively.
$A,B,C,$
and D, respectively.
Proposition 2.15. Suppose that f is faithfully flat and quasi-compact, both B and C are tori, and
![]() $\ker (f)$
is a smooth group
$\ker (f)$
is a smooth group
![]() $\mathcal{O}_K$
-scheme with connected fibers. Then,
$\mathcal{O}_K$
-scheme with connected fibers. Then,
![]() $\mathcal{D}$
is a parahoric group
$\mathcal{D}$
is a parahoric group
![]() $\mathcal{O}_K$
-scheme. Moreover, if
$\mathcal{O}_K$
-scheme. Moreover, if
![]() $\mathcal{A}=\mathcal{G}_x^\circ $
, then
$\mathcal{A}=\mathcal{G}_x^\circ $
, then
![]() $\mathcal{D}=\mathcal{G}^\circ _{(x,\ast )}$
under the isomorphism
$\mathcal{D}=\mathcal{G}^\circ _{(x,\ast )}$
under the isomorphism
from Proposition 2.5.
Proof. By Proposition 2.14, we know that
![]() $\mathcal{D}$
is a smooth group
$\mathcal{D}$
is a smooth group
![]() $\mathcal{O}_K$
-scheme with connected fibers. Moreover, observe that we have a natural short exact sequence of group
$\mathcal{O}_K$
-scheme with connected fibers. Moreover, observe that we have a natural short exact sequence of group
![]() $\mathcal{O}_K$
-schemes
$\mathcal{O}_K$
-schemes
where the map
![]() $\mathcal{A}\times _{\mathrm{Spec}\,(\mathcal{O}_K)}\mathcal{C}\to \mathcal{B}$
is given by sending
$\mathcal{A}\times _{\mathrm{Spec}\,(\mathcal{O}_K)}\mathcal{C}\to \mathcal{B}$
is given by sending
![]() $(a,c)$
to
$(a,c)$
to
![]() $f(a)g(c)^{-1}$
. This implies that D is a normal subgroup of the reductive group
$f(a)g(c)^{-1}$
. This implies that D is a normal subgroup of the reductive group
![]() $A\times _{\mathrm{Spec}\,(K)}C$
and so reductive (see [Reference MilneMil17, Corollary 21.53]).
$A\times _{\mathrm{Spec}\,(K)}C$
and so reductive (see [Reference MilneMil17, Corollary 21.53]).
On the other hand, this exact sequence also implies that
![]() ${D}\to {A}\times _{\mathrm{Spec}\,(K)}{C}$
induces an isomorphism on adjoint subgroups as
${D}\to {A}\times _{\mathrm{Spec}\,(K)}{C}$
induces an isomorphism on adjoint subgroups as
![]() ${B}$
is abelian. Moreover, observe that evidently
${B}$
is abelian. Moreover, observe that evidently
The claim then follows directly from Proposition 2.13.
Torsors for fiber products of groups
We next are interested in understanding the relationship between torsors for a fiber product of groups, and torsors for their constituent groups. The correct generality for this discussion is that of topoi. We follow the notation and conventions concerning torsors and topoi as found in [Reference Imai, Kato and YoucisIKY24a, Reference Imai, Kato and YoucisIKY24b, §A.1].
Let us fix a topos
![]() $\mathscr {T}$
with final object
$\mathscr {T}$
with final object
![]() $\ast $
, and a Cartesian diagram of group objects
$\ast $
, and a Cartesian diagram of group objects

Consider the
![]() $2$
-fiber product of groupoids
$2$
-fiber product of groupoids
(e.g., see [SP17, Tag 02X9]). Observe that there is a natural equivalence of functors
and thus the triple
![]() $(p_\ast ,q_\ast ,\theta _{\textrm {nat}})$
determines an object of the
$(p_\ast ,q_\ast ,\theta _{\textrm {nat}})$
determines an object of the
![]() $2$
-fiber product. Thus,
$2$
-fiber product. Thus,
given by
![]() $\Psi (\mathcal{P})=(p_\ast \mathcal{P},q_\ast \mathcal{P},\theta _{\textrm {nat}})$
is a morphism of groupoids.
$\Psi (\mathcal{P})=(p_\ast \mathcal{P},q_\ast \mathcal{P},\theta _{\textrm {nat}})$
is a morphism of groupoids.
Conversely, suppose that
![]() $(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
is an object of
$(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
is an object of
![]() $\mathbf {Tors}_{\mathcal{A}}(\mathscr {T})\times _{f_\ast ,\mathbf {Tors}_{\mathcal{B}}(\mathscr {T}),g_\ast }\mathbf {Tors}_{\mathcal{C}}(\mathscr {T})$
. Let us observe that we have a natural map
$\mathbf {Tors}_{\mathcal{A}}(\mathscr {T})\times _{f_\ast ,\mathbf {Tors}_{\mathcal{B}}(\mathscr {T}),g_\ast }\mathbf {Tors}_{\mathcal{C}}(\mathscr {T})$
. Let us observe that we have a natural map
induced by the map
![]() $(e,\textrm {id})\colon \mathcal{Q}_{\mathcal{A}}\to \mathcal{B}\times \mathcal{Q}_{\mathcal{A}}$
, where e denotes the identity section of
$(e,\textrm {id})\colon \mathcal{Q}_{\mathcal{A}}\to \mathcal{B}\times \mathcal{Q}_{\mathcal{A}}$
, where e denotes the identity section of
![]() $\mathcal{B}$
. We similarly have a map
$\mathcal{B}$
. We similarly have a map
![]() $\mathcal{Q}_{\mathcal{C}}\to g_\ast \mathcal{Q}_{\mathcal{C}}$
. Let us define
$\mathcal{Q}_{\mathcal{C}}\to g_\ast \mathcal{Q}_{\mathcal{C}}$
. Let us define

where this limit is taken in
![]() $\mathscr {T}$
. It is simple to check that there is a unique
$\mathscr {T}$
. It is simple to check that there is a unique
![]() $\mathcal{D}$
-action on
$\mathcal{D}$
-action on
![]() $\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
for which the natural map
$\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
for which the natural map
![]() $\mathcal{Q}_{\mathcal{A}}\times _{\theta }\mathcal{Q}_{\mathcal{C}}\to \mathcal{Q}_{\mathcal{A}}\times \mathcal{Q}_{\mathcal{C}}$
is equivariant for the map
$\mathcal{Q}_{\mathcal{A}}\times _{\theta }\mathcal{Q}_{\mathcal{C}}\to \mathcal{Q}_{\mathcal{A}}\times \mathcal{Q}_{\mathcal{C}}$
is equivariant for the map
![]() $\mathcal{D}\to \mathcal{A}\times \mathcal{C}$
. This
$\mathcal{D}\to \mathcal{A}\times \mathcal{C}$
. This
![]() $\mathcal{D}$
-object of
$\mathcal{D}$
-object of
![]() $\mathscr {T}$
is evidently functorial in the triple
$\mathscr {T}$
is evidently functorial in the triple
![]() $(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
.
$(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
.
Note that it is not a priori clear that
![]() $\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
is a
$\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
is a
![]() $\mathcal{D}$
-torsor. That said, we do have the following affirmative result in this direction under the assumption that f is an epimorphism.
$\mathcal{D}$
-torsor. That said, we do have the following affirmative result in this direction under the assumption that f is an epimorphism.
Proposition 2.16. Suppose that f is an epimorphism. Then, the functor
given by
![]() $\Phi (\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )=\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
, is a well-defined quasi-inverse to
$\Phi (\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )=\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
, is a well-defined quasi-inverse to
![]() $\Psi $
. Moreover, the equivalences
$\Psi $
. Moreover, the equivalences
![]() $\Psi $
and
$\Psi $
and
![]() $\Phi $
are compatible with pullbacks along a morphism of topoi
$\Phi $
are compatible with pullbacks along a morphism of topoi
![]() $\mathscr {T}'\to \mathscr {T}\kern-1pt$
.
$\mathscr {T}'\to \mathscr {T}\kern-1pt$
.
Proof. To show that
![]() $\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
is a
$\mathcal{Q}_{\mathcal{A}}\times _\theta \mathcal{Q}_{\mathcal{C}}$
is a
![]() $\mathcal{D}$
-torsor we are free to localize
$\mathcal{D}$
-torsor we are free to localize
![]() $\mathscr {T}$
. In particular, we may assume that
$\mathscr {T}$
. In particular, we may assume that
![]() $\mathcal{Q}_{\mathcal{C}}$
is trivializable. Choose a trivialization corresponding to an element x of
$\mathcal{Q}_{\mathcal{C}}$
is trivializable. Choose a trivialization corresponding to an element x of
![]() $\mathcal{Q}_{\mathcal{C}}(\ast )$
. Consider then the induced element of
$\mathcal{Q}_{\mathcal{C}}(\ast )$
. Consider then the induced element of
![]() $g_\ast \mathcal{Q}_{\mathcal{C}}(\ast )$
, which we also denote by x, and the resulting element
$g_\ast \mathcal{Q}_{\mathcal{C}}(\ast )$
, which we also denote by x, and the resulting element
![]() $\theta ^{-1}(x)$
of
$\theta ^{-1}(x)$
of
![]() $f_\ast \mathcal{Q}_{\mathcal{A}}(\ast )$
. As f is an epimorphism we may, after possibly localizing
$f_\ast \mathcal{Q}_{\mathcal{A}}(\ast )$
. As f is an epimorphism we may, after possibly localizing
![]() $\mathscr {T}$
further, assume that there exists some element y of
$\mathscr {T}$
further, assume that there exists some element y of
![]() $\mathcal{Q}_{\mathcal{A}}(\ast )$
mapping to
$\mathcal{Q}_{\mathcal{A}}(\ast )$
mapping to
![]() $\theta ^{-1}(x)$
. These compatible elements define an isomorphism of diagrams
$\theta ^{-1}(x)$
. These compatible elements define an isomorphism of diagrams

As
![]() $\mathcal{A}\times _{\textrm {id}}\mathcal{C}$
is evidently the trivial
$\mathcal{A}\times _{\textrm {id}}\mathcal{C}$
is evidently the trivial
![]() $\mathcal{D}$
-torsor, the claim follows.
$\mathcal{D}$
-torsor, the claim follows.
To prove that
![]() $\Phi \circ \Psi $
is naturally isomorphic to the identity, it suffices to prove the following claim: for a
$\Phi \circ \Psi $
is naturally isomorphic to the identity, it suffices to prove the following claim: for a
![]() $\mathcal{D}$
-torsor
$\mathcal{D}$
-torsor
![]() $\mathcal{P}$
the natural map
$\mathcal{P}$
the natural map
is equivariant for the map
![]() $\mathcal{D}\to \mathcal{A}\times \mathcal{C}$
, and factorizes uniquely through a
$\mathcal{D}\to \mathcal{A}\times \mathcal{C}$
, and factorizes uniquely through a
![]() $\mathcal{D}$
-equivariant map
$\mathcal{D}$
-equivariant map
![]() $\mathcal{P}\to f_\ast \mathcal{P}\times _\theta g_\ast \mathcal{P}$
. But this claim can be checked after localizing on
$\mathcal{P}\to f_\ast \mathcal{P}\times _\theta g_\ast \mathcal{P}$
. But this claim can be checked after localizing on
![]() $\mathscr {T}$
, which reduces us to the trivial case as in the previous paragraph.
$\mathscr {T}$
, which reduces us to the trivial case as in the previous paragraph.
To prove that
![]() $\Psi \circ \Phi $
is naturally isomorphic to the identity, let us fix an object
$\Psi \circ \Phi $
is naturally isomorphic to the identity, let us fix an object
![]() $(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
of the
$(\mathcal{Q}_{\mathcal{A}},\mathcal{Q}_{\mathcal{C}},\theta )$
of the
![]() $2$
-fiber product. Let us observe that we have a natural projection map
$2$
-fiber product. Let us observe that we have a natural projection map
which is equivariant for the map
![]() $\mathcal{D}\to \mathcal{A}$
. By the adjunction in [Reference GiraudGir71, Chapitre III, Proposition 1.3.6 (iii)] we obtain a unique
$\mathcal{D}\to \mathcal{A}$
. By the adjunction in [Reference GiraudGir71, Chapitre III, Proposition 1.3.6 (iii)] we obtain a unique
![]() $\mathcal{A}$
-equivariant map
$\mathcal{A}$
-equivariant map
which is necessarily an isomorphism of
![]() $\mathcal{A}$
-torsors. Similarly, we obtain an isomorphism
$\mathcal{A}$
-torsors. Similarly, we obtain an isomorphism
It is then easy to check that
![]() $(\alpha ,\beta )$
defines a natural morphism
$(\alpha ,\beta )$
defines a natural morphism
where the matching of
![]() $\theta _{\textrm {nat}}$
in the source and
$\theta _{\textrm {nat}}$
in the source and
![]() $\theta $
in the target may be checked locally on
$\theta $
in the target may be checked locally on
![]() $\mathscr {T}$
, from where we may reduce to the trivial case where it is clear. As the
$\mathscr {T}$
, from where we may reduce to the trivial case where it is clear. As the
![]() $2$
-fiber product is a groupoid, we deduce that
$2$
-fiber product is a groupoid, we deduce that
![]() $(\alpha ,\beta )$
is a natural isomorphism.
$(\alpha ,\beta )$
is a natural isomorphism.
The final compatibility claim is clear by construction.
Shtukas for fiber products of groups
We finally record the natural implication of Proposition 2.16 for shtukas over a pre-adic space in the sense of [Reference Pappas and RapoportPR24, §2.3].
To this end, let us fix a fiber product of group
![]() $\mathbb {Z}_p$
-schemes
$\mathbb {Z}_p$
-schemes

where
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\mathcal{B}$
, and
$\mathcal{B}$
, and
![]() $\mathcal{C}$
are smooth group
$\mathcal{C}$
are smooth group
![]() $\mathbb {Z}_p$
-schemes with connected fibers, f is faithfully flat and quasi-compact, and
$\mathbb {Z}_p$
-schemes with connected fibers, f is faithfully flat and quasi-compact, and
![]() $\ker (f)$
is a smooth group
$\ker (f)$
is a smooth group
![]() $\mathbb {Z}_p$
-scheme with connected fibers. We then see by Proposition 2.14 that
$\mathbb {Z}_p$
-scheme with connected fibers. We then see by Proposition 2.14 that
![]() $\mathcal{D}$
is a smooth group
$\mathcal{D}$
is a smooth group
![]() $\mathbb {Z}_p$
-scheme with connected fibers. Further fix a discretely valued algebraic extension E of
$\mathbb {Z}_p$
-scheme with connected fibers. Further fix a discretely valued algebraic extension E of
![]() $\mathbb {Q}_p$
with residue field
$\mathbb {Q}_p$
with residue field
![]() $k_E$
, and fix a pre-adic space
$k_E$
, and fix a pre-adic space
![]() $\mathscr {X}$
over
$\mathscr {X}$
over
![]() $\mathcal{O}_{E}$
. We then have the following result.
$\mathcal{O}_{E}$
. We then have the following result.
Corollary 2.17. There is an equivalence of categories
Proof. Fix an morphism
![]() $\alpha \colon S\to \mathscr {X}^{\lozenge /}$
, where S is an object of
$\alpha \colon S\to \mathscr {X}^{\lozenge /}$
, where S is an object of
![]() $\mathbf {Perf}_{k_E}$
, with corresponding untilt
$\mathbf {Perf}_{k_E}$
, with corresponding untilt
![]() $S^\sharp $
over
$S^\sharp $
over
![]() $\mathcal{O}_{E}$
. Then, it immediately by applying Proposition 2.16 to the étale topoi of
$\mathcal{O}_{E}$
. Then, it immediately by applying Proposition 2.16 to the étale topoi of
![]() $S\dot {\times }\mathbb {Z}_p$
and
$S\dot {\times }\mathbb {Z}_p$
and
![]() $S\dot {\times }\mathbb {Z}_p\setminus S^\sharp $
, that there are equivalences
$S\dot {\times }\mathbb {Z}_p\setminus S^\sharp $
, that there are equivalences
As this equivalence is
![]() $2$
-functorial in the topos, the claim then follows by letting S vary.
$2$
-functorial in the topos, the claim then follows by letting S vary.
3 Integral models of Shimura varieties at parahoric level
In this section we study the Kisin–Pappas–Zhou models of Shimura varieties of abelian type at parahoric level as constructed in [Reference Kisin and PappasKP18] and [Reference Kisin, Pappas and ZhouKPZ24].
3.1 Existence of models and their properties
In this subsection we precisely state the existence of integral models at parahoric level and list some of their properties which are most relevant for our purposes.
Shimura varieties
We begin by recalling some definitions and notation from the theory of Shimura varieties. Let
![]() $(\mathbf {G},\mathbf {X})$
be a Shimura datum, meaning that
$(\mathbf {G},\mathbf {X})$
be a Shimura datum, meaning that
![]() ${\mathbf {G}}$
is a reductive group over
${\mathbf {G}}$
is a reductive group over
![]() $\mathbb {Q}$
, and
$\mathbb {Q}$
, and
![]() $\mathbf {X}$
is a
$\mathbf {X}$
is a
![]() ${\mathbf {G}}(\mathbb {R})$
-conjugacy class of homomorphisms
${\mathbf {G}}(\mathbb {R})$
-conjugacy class of homomorphisms
(where
![]() $\mathbb {S} = {\textrm {Res}}_{\mathbb {C}/\mathbb {R}}\,\mathbb {G}_{m/\mathbb {C}}$
is the Deligne torus), satisfying the axioms (SV1)-(SV3) in [Reference MilneMil05, Definition 5.5]. Associated to
$\mathbb {S} = {\textrm {Res}}_{\mathbb {C}/\mathbb {R}}\,\mathbb {G}_{m/\mathbb {C}}$
is the Deligne torus), satisfying the axioms (SV1)-(SV3) in [Reference MilneMil05, Definition 5.5]. Associated to
![]() $\mathbf {X}$
is a unique conjugacy class
$\mathbf {X}$
is a unique conjugacy class ![]() of coharacters
of coharacters
![]() $\mathbb {G}_{m,\mathbb {C}}\to \mathbf {G}_{\mathbb {C}}$
(see [Reference MilneMil05, p. 344]). We denote the field of definition of
$\mathbb {G}_{m,\mathbb {C}}\to \mathbf {G}_{\mathbb {C}}$
(see [Reference MilneMil05, p. 344]). We denote the field of definition of ![]() by
by
![]() ${\mathbf {E}}$
, and call it the reflex field of
${\mathbf {E}}$
, and call it the reflex field of
![]() $(\mathbf {G},\mathbf {X})$
(see [Reference MilneMil05, Definition 12.2]).
$(\mathbf {G},\mathbf {X})$
(see [Reference MilneMil05, Definition 12.2]).
We often fix a place v of
![]() $\mathbf {E}$
dividing p, and write E for the completion
$\mathbf {E}$
dividing p, and write E for the completion
![]() $\mathbf {E}_v$
. Using [Reference KottwitzKot84, Lemma 1.1.3],
$\mathbf {E}_v$
. Using [Reference KottwitzKot84, Lemma 1.1.3], ![]() gives rise to a unique conjugacy class of cocharacters
gives rise to a unique conjugacy class of cocharacters
![]() $\mathbb {G}_{m,\overline {E}}\to G_{\overline {E}}$
, which we also denote by
$\mathbb {G}_{m,\overline {E}}\to G_{\overline {E}}$
, which we also denote by ![]() . One may check that this conjugacy class has field of definition E, and so we call this the local reflex field.
. One may check that this conjugacy class has field of definition E, and so we call this the local reflex field.
For any neat compact open subgroup
![]() $\mathsf {K} \subseteq {\mathbf {G}}(\mathbb {A}_f)$
(see [Reference MilneMil05, p. 288]), we attach to
$\mathsf {K} \subseteq {\mathbf {G}}(\mathbb {A}_f)$
(see [Reference MilneMil05, p. 288]), we attach to
![]() $(\mathbf {G},\mathbf {X})$
and
$(\mathbf {G},\mathbf {X})$
and
![]() $\mathsf {K}$
the Shimura variety
$\mathsf {K}$
the Shimura variety
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, which is a quasi-projective variety over
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, which is a quasi-projective variety over
![]() $\mathbb {C}$
, whose
$\mathbb {C}$
, whose
![]() $\mathbb {C}$
-points are given by the equality
$\mathbb {C}$
-points are given by the equality
We write an element of this double quotient as
![]() $[x,g]_{\mathsf {K}}$
. As in [Reference DeligneDel79] (cf. [Reference MoonenMoo98]),
$[x,g]_{\mathsf {K}}$
. As in [Reference DeligneDel79] (cf. [Reference MoonenMoo98]),
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
admits a canonical model over the reflex field
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
admits a canonical model over the reflex field
![]() ${\mathbf {E}}$
. Hereafter we will use
${\mathbf {E}}$
. Hereafter we will use
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
to denote the canonical model over
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
to denote the canonical model over
![]() ${\mathbf {E}}$
.
${\mathbf {E}}$
.
For a containment
![]() $\mathsf {K} \subseteq \mathsf {K}'$
of neat compact open subgroups of
$\mathsf {K} \subseteq \mathsf {K}'$
of neat compact open subgroups of
![]() ${\mathbf {G}}(\mathbb {A}_f)$
and g in
${\mathbf {G}}(\mathbb {A}_f)$
and g in
![]() ${\mathbf {G}}(\mathbb {A}_f)$
such that
${\mathbf {G}}(\mathbb {A}_f)$
such that
![]() $g^{-1}\mathsf {K} g \subseteq \mathsf {K}'$
, there is a unique finite étale morphism of
$g^{-1}\mathsf {K} g \subseteq \mathsf {K}'$
, there is a unique finite étale morphism of
![]() ${\mathbf {E}}$
-schemes
${\mathbf {E}}$
-schemes
which is given on
![]() $\mathbb {C}$
-points by the identity
$\mathbb {C}$
-points by the identity
We write
![]() $\pi _{\mathsf {K},\mathsf {K}'}$
for
$\pi _{\mathsf {K},\mathsf {K}'}$
for
![]() $t_{\mathsf {K},\mathsf {K}'}(\text {id})$
, and
$t_{\mathsf {K},\mathsf {K}'}(\text {id})$
, and
![]() $[g]_{\mathsf { K}}$
for
$[g]_{\mathsf { K}}$
for
![]() $t_{\mathsf {K}, g^{-1}\mathsf {K} g}(g)$
.
$t_{\mathsf {K}, g^{-1}\mathsf {K} g}(g)$
.
The morphisms
![]() $\pi _{\mathsf {K},\mathsf {K}'}$
form a projective system
$\pi _{\mathsf {K},\mathsf {K}'}$
form a projective system
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}}$
with finite étale transition morphisms. We define
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}}$
with finite étale transition morphisms. We define
where the limit is taken over all neat compact open subgroups
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() ${\mathbf {G}}(\mathbb {A}_f)$
. Since each
${\mathbf {G}}(\mathbb {A}_f)$
. Since each
![]() $\pi _{\mathsf {K},\mathsf {K}'}$
is affine, the limit in (3.1) exists as an
$\pi _{\mathsf {K},\mathsf {K}'}$
is affine, the limit in (3.1) exists as an
![]() ${\mathbf {E}}$
-scheme (see [SP17, Tag 01YX]). The morphisms
${\mathbf {E}}$
-scheme (see [SP17, Tag 01YX]). The morphisms
![]() $[g]_{\mathsf {K}}$
endow
$[g]_{\mathsf {K}}$
endow
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})$
with a continuous action of
$\textrm {Sh}(\mathbf {G},\mathbf {X})$
with a continuous action of
![]() ${\mathbf {G}}(\mathbb {A}_f)$
in the sense of [Reference DeligneDel79, 2.7.1].
${\mathbf {G}}(\mathbb {A}_f)$
in the sense of [Reference DeligneDel79, 2.7.1].
We will often fix a prime p and consider neat compact open subgroups
![]() $\mathsf {K} = \mathsf {K}_p \mathsf {K}^p$
with
$\mathsf {K} = \mathsf {K}_p \mathsf {K}^p$
with
![]() $\mathsf {K}_p \subseteq {\mathbf {G}}(\mathbb {Q}_p)$
and
$\mathsf {K}_p \subseteq {\mathbf {G}}(\mathbb {Q}_p)$
and
![]() $\mathsf {K}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
. We define
$\mathsf {K}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
. We define
where
![]() $\mathsf {K}^{p}$
varies over neat compact open subgroups of
$\mathsf {K}^{p}$
varies over neat compact open subgroups of
![]() ${\mathbf {G}}(\mathbb {A}_f^p)$
. As in the case of
${\mathbf {G}}(\mathbb {A}_f^p)$
. As in the case of
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})$
, we see that
$\textrm {Sh}(\mathbf {G},\mathbf {X})$
, we see that
![]() $\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})$
is a scheme over
$\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})$
is a scheme over
![]() ${\mathbf {E}}$
with a continuous action of
${\mathbf {E}}$
with a continuous action of
![]() ${\mathbf {G}}(\mathbb {A}_f^p)$
.
${\mathbf {G}}(\mathbb {A}_f^p)$
.
Remark 3.1. When several Shimura data are simultaneously under consideration, we will differentiate them with numerical subscripts (e.g.,
![]() $(\mathbf {G}_1,\mathbf {X}_1)$
) and use the same numerical subscripts to denote the objects defined above (or below) for this Shimura datum (e.g.,
$(\mathbf {G}_1,\mathbf {X}_1)$
) and use the same numerical subscripts to denote the objects defined above (or below) for this Shimura datum (e.g.,
![]() $\textrm {Sh}_{\mathsf {K}_{p,1}\mathsf {K}^p_1}(\mathbf {G}_1,\mathbf {X}_1)$
).
$\textrm {Sh}_{\mathsf {K}_{p,1}\mathsf {K}^p_1}(\mathbf {G}_1,\mathbf {X}_1)$
).
A morphism of Shimura data
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is a morphism of group
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is a morphism of group
![]() $\mathbb {Q}$
-schemes
$\mathbb {Q}$
-schemes
![]() $\alpha \colon \mathbf {G}_1\to \mathbf {G}$
with the property that
$\alpha \colon \mathbf {G}_1\to \mathbf {G}$
with the property that
![]() $\alpha _{\mathbb {R}}\circ h_1$
belongs to
$\alpha _{\mathbb {R}}\circ h_1$
belongs to
![]() $\mathbf {X}$
for
$\mathbf {X}$
for
![]() $h_1$
in
$h_1$
in
![]() $\mathbf {X}_1$
. We say that
$\mathbf {X}_1$
. We say that
![]() $\alpha $
is an embedding if
$\alpha $
is an embedding if
![]() $\mathbf {G}_1\to \mathbf {G}$
is a closed embedding. From [Reference DeligneDel79, §5], for a morphism of Shimura data
$\mathbf {G}_1\to \mathbf {G}$
is a closed embedding. From [Reference DeligneDel79, §5], for a morphism of Shimura data
![]() $\alpha $
, one has that
$\alpha $
, one has that
![]() $\mathbf {E}\subseteq \mathbf {E}_1$
and there is a unique morphism
$\mathbf {E}\subseteq \mathbf {E}_1$
and there is a unique morphism
![]() $\textrm {Sh}(\mathbf {G}_1,\mathbf {X}_1)\to \textrm {Sh}(\mathbf {G},\mathbf {X})_{\mathbf {E}_1}$
of
$\textrm {Sh}(\mathbf {G}_1,\mathbf {X}_1)\to \textrm {Sh}(\mathbf {G},\mathbf {X})_{\mathbf {E}_1}$
of
![]() $\mathbf {E}_1$
-schemes equivariant for the map
$\mathbf {E}_1$
-schemes equivariant for the map
![]() $\alpha \colon \mathbf {G}_1(\mathbb {A}_f)\to \mathbf {G}(\mathbb {A}_f)$
and such that if
$\alpha \colon \mathbf {G}_1(\mathbb {A}_f)\to \mathbf {G}(\mathbb {A}_f)$
and such that if
![]() $\alpha (\mathsf {K}_1)\subseteq \mathsf {K}$
then the induced map on the quotients
$\alpha (\mathsf {K}_1)\subseteq \mathsf {K}$
then the induced map on the quotients
![]() $\alpha _{\mathsf {K}_1,\mathsf {K}}\colon \textrm {Sh}_{\mathsf {K}_1}(\mathbf {G},\mathbf {X})\to \textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_{E_1}$
is given on
$\alpha _{\mathsf {K}_1,\mathsf {K}}\colon \textrm {Sh}_{\mathsf {K}_1}(\mathbf {G},\mathbf {X})\to \textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_{E_1}$
is given on
![]() $\mathbb {C}$
-points by
$\mathbb {C}$
-points by
We say that
![]() $\alpha $
is an ad-isomorphism if
$\alpha $
is an ad-isomorphism if
![]() $\alpha \colon \mathbf {G}_1\to \mathbf {G}$
is an ad-isomorphism and moreover, that
$\alpha \colon \mathbf {G}_1\to \mathbf {G}$
is an ad-isomorphism and moreover, that
![]() $\alpha \colon (\mathbf {G}_1^{\textrm {ad}},\mathbf {X}_1^{\textrm {ad}})\to (\mathbf {G}^{\textrm {ad}},\mathbf {X}^{\textrm {ad}})$
is an isomorphism.
$\alpha \colon (\mathbf {G}_1^{\textrm {ad}},\mathbf {X}_1^{\textrm {ad}})\to (\mathbf {G}^{\textrm {ad}},\mathbf {X}^{\textrm {ad}})$
is an isomorphism.
Parahoric Shimura data
We say that a triple
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum if
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum if
![]() $(\mathbf {G},\mathbf {X})$
is a Shimura datum, and
$(\mathbf {G},\mathbf {X})$
is a Shimura datum, and
![]() $\mathcal{G}$
is a parahoric model of
$\mathcal{G}$
is a parahoric model of ![]() . By a morphism
. By a morphism
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
of parahoric Shimura data we mean a morphism
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
of parahoric Shimura data we mean a morphism
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
of Shimura data together with a specified model
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
of Shimura data together with a specified model
![]() $\mathcal{G}_1\to \mathcal{G}$
of
$\mathcal{G}_1\to \mathcal{G}$
of
![]() $G_1\to G$
, which we also denote
$G_1\to G$
, which we also denote
![]() $\alpha $
. By [Reference Kaletha and PrasadKP23, Corollary 2.10.10], such an
$\alpha $
. By [Reference Kaletha and PrasadKP23, Corollary 2.10.10], such an
![]() $\alpha $
is unique, and it exists if and only if
$\alpha $
is unique, and it exists if and only if
![]() $\alpha \colon G(\breve {\mathbb {Q}}_p)\to G_1(\breve {\mathbb {Q}}_p)$
maps
$\alpha \colon G(\breve {\mathbb {Q}}_p)\to G_1(\breve {\mathbb {Q}}_p)$
maps
![]() $\mathcal{G}_1(\breve {\mathbb {Z}}_p)$
into
$\mathcal{G}_1(\breve {\mathbb {Z}}_p)$
into
![]() $\mathcal{G}(\breve {\mathbb {Z}}_p)$
. We say that
$\mathcal{G}(\breve {\mathbb {Z}}_p)$
. We say that
![]() $\alpha $
is an embedding or an ad-isomorphism if
$\alpha $
is an embedding or an ad-isomorphism if
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is.
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is.
Given a parahoric Shimura datum
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
we often use the following shorthand
$(\mathbf {G},\mathbf {X},\mathcal{G})$
we often use the following shorthand
Choosing a point x of
![]() $\mathscr {B}(G,\mathbb {Q}_p)$
such that
$\mathscr {B}(G,\mathbb {Q}_p)$
such that
![]() $\mathcal{G}=\mathcal{G}_x^\circ $
, we write
$\mathcal{G}=\mathcal{G}_x^\circ $
, we write
which is a a supergroup of
![]() $\mathsf {K}_p$
of finite index.
$\mathsf {K}_p$
of finite index.
The following lemma will be important for later constructions. Let us denote by
![]() $\mathbf {E}^p$
the maximal extension of
$\mathbf {E}^p$
the maximal extension of
![]() $\mathbf {E}$
unramified at places dividing p.
$\mathbf {E}$
unramified at places dividing p.
Lemma 3.2 ([Reference Kisin and PappasKP18, Corollary 4.3.9]).
The natural map
is a bijection.
In other words, this result says that the action of
![]() $\text {Gal}(\overline {\mathbf {E}}/\mathbf {E})$
on
$\text {Gal}(\overline {\mathbf {E}}/\mathbf {E})$
on
![]() $\pi _0(\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{\overline {\mathbf {E}}})$
factorizes through
$\pi _0(\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{\overline {\mathbf {E}}})$
factorizes through
![]() $\text {Gal}(\mathbf {E}^p/\mathbf {E})$
(cf. [SP17, Tag 038D]).
$\text {Gal}(\mathbf {E}^p/\mathbf {E})$
(cf. [SP17, Tag 038D]).
Some conditions on a Shimura datum
The construction of Kisin–Pappas–Zhou models involves several conditions on a Shimura datum that we presently recall.
We start with the following standard definitions, in increasing level of generality.
Definition 3.3. We say that
![]() $(\mathbf {G},\mathbf {X})$
is
$(\mathbf {G},\mathbf {X})$
is
-
⋄ of Siegel type if it is of the form
 $(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^{\pm })$
where
$(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^{\pm })$
where
 $\mathbf {V}$
is a symplectic
$\mathbf {V}$
is a symplectic
 $\mathbb {Q}$
-space, and
$\mathbb {Q}$
-space, and
 $\mathfrak {h}^{\pm }$
is the union of the upper and lower Siegel half-spaces (e.g., see [Reference MilneMil05, §6]),
$\mathfrak {h}^{\pm }$
is the union of the upper and lower Siegel half-spaces (e.g., see [Reference MilneMil05, §6]), -
⋄ of Hodge type if there exists an embedding of Shimura data
 $\iota \colon (\mathbf {G},\mathbf {X})\to (\textrm {GSp}(\mathbf {V}),\mathfrak {h}^{\pm })$
(called a Hodge embedding),
$\iota \colon (\mathbf {G},\mathbf {X})\to (\textrm {GSp}(\mathbf {V}),\mathfrak {h}^{\pm })$
(called a Hodge embedding), -
⋄ of abelian type if there exists a Shimura datum
 $(\mathbf {G}_1,\mathbf {X}_1)$
of Hodge type and an isogeny
$(\mathbf {G}_1,\mathbf {X}_1)$
of Hodge type and an isogeny
 $\alpha \colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
inducing an isomorphism
$\alpha \colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
inducing an isomorphism
 $(\mathbf {G}_1^{\text {ad}},\mathbf {X}^{\text {ad}})\to (\mathbf {G}^{\text {ad}},\mathbf {X}^{\text {ad}})$
, in which case we say that
$(\mathbf {G}_1^{\text {ad}},\mathbf {X}^{\text {ad}})\to (\mathbf {G}^{\text {ad}},\mathbf {X}^{\text {ad}})$
, in which case we say that
 $(\mathbf {G}_1,\mathbf {X}_1)$
is adapted to
$(\mathbf {G}_1,\mathbf {X}_1)$
is adapted to
 $(\mathbf {G},\mathbf {X})$
, leaving the
$(\mathbf {G},\mathbf {X})$
, leaving the
 $\alpha $
implicit.
$\alpha $
implicit.
We have the following examples of Shimura data of abelian type.Footnote 5
Example 3.4. Shimura data of PEL type (see [Reference MilneMil05, §8]) are of Hodge type.
Example 3.5. Let
![]() $\mathbf {V}$
be a quadratic space over
$\mathbf {V}$
be a quadratic space over
![]() $\mathbb {Q}$
of signature
$\mathbb {Q}$
of signature
![]() $(n,2)$
. The group
$(n,2)$
. The group
![]() $\textrm {GSpin}(\mathbf {V})$
acts transitively on the space
$\textrm {GSpin}(\mathbf {V})$
acts transitively on the space
![]() $\mathbf {X}$
of oriented negative definite
$\mathbf {X}$
of oriented negative definite
![]() $2$
-planes in
$2$
-planes in
![]() $\mathbf {V}_{\mathbb {R}}$
, and
$\mathbf {V}_{\mathbb {R}}$
, and
![]() $\mathbf {X}$
can be identified with a
$\mathbf {X}$
can be identified with a
![]() $\textrm {GSpin}(\mathbf {V})(\mathbb {R})$
-conjugacy class of morphisms
$\textrm {GSpin}(\mathbf {V})(\mathbb {R})$
-conjugacy class of morphisms
![]() $\mathbb {S}\to \textrm {GSpin}(\mathbf {V})_{\mathbb {R}}$
(see [Reference PeraMP16, §1]). The pair
$\mathbb {S}\to \textrm {GSpin}(\mathbf {V})_{\mathbb {R}}$
(see [Reference PeraMP16, §1]). The pair
![]() $(\textrm {GSpin}(\mathbf {V}),\mathbf {X})$
is a Shimura datum of Hodge type which is not of PEL type (see [Reference PeraMP16, §3]).
$(\textrm {GSpin}(\mathbf {V}),\mathbf {X})$
is a Shimura datum of Hodge type which is not of PEL type (see [Reference PeraMP16, §3]).
Example 3.6. Let
![]() $F\supsetneq \mathbb {Q}$
be a totally real field, B a quaternion algebra over F, and
$F\supsetneq \mathbb {Q}$
be a totally real field, B a quaternion algebra over F, and
![]() $\mathbf {G}_B$
the algebraic
$\mathbf {G}_B$
the algebraic
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $B^\times $
. There is a Shimura datum
$B^\times $
. There is a Shimura datum
![]() $(\mathbf {G}_B,\mathbf {X}_B)$
associated to B (see [Reference MilneMil05, Example 5.24]). Then
$(\mathbf {G}_B,\mathbf {X}_B)$
associated to B (see [Reference MilneMil05, Example 5.24]). Then
![]() $(\mathbf {G}_B,\mathbf {X}_B)$
is of abelian type, but not of Hodge type. The Shimura varieties associated to such
$(\mathbf {G}_B,\mathbf {X}_B)$
is of abelian type, but not of Hodge type. The Shimura varieties associated to such
![]() $(\mathbf {G}_B,\mathbf {X}_B)$
include Shimura curves.
$(\mathbf {G}_B,\mathbf {X}_B)$
include Shimura curves.
Example 3.7. For a
![]() $\mathbb {Q}$
-torus
$\mathbb {Q}$
-torus
![]() $\mathbf {T}$
any homomorphism
$\mathbf {T}$
any homomorphism
![]() $h\colon \mathbb {S}\to \mathbf {T}_{\mathbb {R}}$
defines a Shimura datum
$h\colon \mathbb {S}\to \mathbf {T}_{\mathbb {R}}$
defines a Shimura datum
![]() $(\mathbf {T},\{h\})$
of abelian type, which is rarely of Hodge type, and which we refer to as being of toral type.
$(\mathbf {T},\{h\})$
of abelian type, which is rarely of Hodge type, and which we refer to as being of toral type.
We say that a parahoric Shimura datum
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type or abelian type if the underlying Shimura datum
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type or abelian type if the underlying Shimura datum
![]() $(\mathbf {G},\mathbf {X})$
is.
$(\mathbf {G},\mathbf {X})$
is.
Definition 3.8. A parahoric Shimura datum
![]() $(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
of Hodge type is well-adapted to
$(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
of Hodge type is well-adapted to
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
when given an isogeny
$(\mathbf {G},\mathbf {X},\mathcal{G})$
when given an isogeny
![]() $\alpha \colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
(often left implicit) such that
$\alpha \colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
(often left implicit) such that
-
1.
 $\alpha $
adapts
$\alpha $
adapts
 $(\mathbf {G}_1,\mathbf {X}_1)$
to
$(\mathbf {G}_1,\mathbf {X}_1)$
to
 $(\mathbf {G},\mathbf {X})$
,
$(\mathbf {G},\mathbf {X})$
, -
2. if the isomorphism
induced from the isogeny
 $\alpha \colon G_1^{\mathrm {der}}\to G^{\mathrm {der}}$
and Lemma 2.5 has the property that if
$\alpha \colon G_1^{\mathrm {der}}\to G^{\mathrm {der}}$
and Lemma 2.5 has the property that if
 $\mathcal{G}\simeq \mathcal{G}_x^\circ $
for x, and
$\mathcal{G}\simeq \mathcal{G}_x^\circ $
for x, and
 $x_1$
denotes the corresponding point in
$x_1$
denotes the corresponding point in
 $\mathscr {B}(G_1,\mathbb {Q}_p)$
, then
$\mathscr {B}(G_1,\mathbb {Q}_p)$
, then
 $\mathcal{G}_1\simeq \mathcal{G}_{x_1}^\circ $
,
$\mathcal{G}_1\simeq \mathcal{G}_{x_1}^\circ $
,
-
3. if
 , then
, then
 $\mathbf {E}'$
splits completely at every prime of
$\mathbf {E}'$
splits completely at every prime of
 $\mathbf {E}$
lying over p.
$\mathbf {E}$
lying over p.
Finally, we set some terminology used later on in the article. Let
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura datum of Hodge type. We call a map of Shimura data
$(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura datum of Hodge type. We call a map of Shimura data
where
![]() $\mathbf {V}$
a symplectic
$\mathbf {V}$
a symplectic
![]() $\mathbb {Q}$
-space and
$\mathbb {Q}$
-space and
![]() $\Lambda \subseteq \mathbf {V}_{\mathbb {Q}_p}$
is a self-dual
$\Lambda \subseteq \mathbf {V}_{\mathbb {Q}_p}$
is a self-dual
![]() $\mathbb {Z}_p$
-lattice, a Hodge embedding of parahoric Shimura data if the underling map
$\mathbb {Z}_p$
-lattice, a Hodge embedding of parahoric Shimura data if the underling map
![]() $\iota \colon \mathbf {G}\to \textrm {GSp}(\mathbf {V})$
is a closed embedding. We say that
$\iota \colon \mathbf {G}\to \textrm {GSp}(\mathbf {V})$
is a closed embedding. We say that
![]() $\iota $
respects stabilizers if
$\iota $
respects stabilizers if
![]() $\widetilde {\mathsf {K}}_p=\textrm {GSp}(\Lambda )\cap \mathbf {G}(\mathbb {Q}_p)$
.
$\widetilde {\mathsf {K}}_p=\textrm {GSp}(\Lambda )\cap \mathbf {G}(\mathbb {Q}_p)$
.
Existence and properties of models
We are now prepared to state the existence of Kisin–Pappas–Zhou models, as well as the major properties we need of these models.
Theorem 3.9 ([Reference Kisin, Pappas and ZhouKPZ24, Theorem 7.2.20]).
Suppose that
![]() $p>2$
and
$p>2$
and
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Then, there exists a system
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Then, there exists a system
![]() $\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}$
of normal flat quasi-projective
$\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})\}$
of normal flat quasi-projective
![]() $\mathcal{O}_E$
-models of
$\mathcal{O}_E$
-models of
![]() $\{\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})_E\}$
such that the following properties hold.
$\{\textrm {Sh}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})_E\}$
such that the following properties hold.
-
(1) Fix neat compact open subgroups
 $\mathsf {K}^p$
and
$\mathsf {K}^p$
and
 ${\mathsf {K}^{p}}'$
in
${\mathsf {K}^{p}}'$
in
 $\mathbf {G}(\mathbb {A}_f^p)$
and an element g of
$\mathbf {G}(\mathbb {A}_f^p)$
and an element g of
 $\mathbf {G}(\mathbb {A}_f^p)$
with
$\mathbf {G}(\mathbb {A}_f^p)$
with
 $g^{-1}\mathsf {K}^p g\subseteq {\mathsf {K}^{p}}'$
. Write
$g^{-1}\mathsf {K}^p g\subseteq {\mathsf {K}^{p}}'$
. Write
 $\mathsf {K}=\mathsf {K}_p\mathsf {K}^p$
and
$\mathsf {K}=\mathsf {K}_p\mathsf {K}^p$
and
 $\mathsf {K}'=\mathsf {K}_p{\mathsf {K}^p}'$
. Then, the morphism admits a (necessarily unique) finite étale extension
$\mathsf {K}'=\mathsf {K}_p{\mathsf {K}^p}'$
. Then, the morphism admits a (necessarily unique) finite étale extension $$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g): \mathrm{Sh}_{\mathsf{K}}(\mathbf{G},\mathbf{X})_E\to \mathrm{Sh}_{\mathsf{K}'}(\mathbf{G},\mathbf{X})_E, \end{align*} $$
$$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g): \mathrm{Sh}_{\mathsf{K}}(\mathbf{G},\mathbf{X})_E\to \mathrm{Sh}_{\mathsf{K}'}(\mathbf{G},\mathbf{X})_E, \end{align*} $$
 $$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g): \mathscr{S}_{\mathsf{K}}^{\mathfrak{d}}(\mathbf{G},\mathbf{X})\to \mathscr{S}_{\mathsf{K}'}^{\mathfrak{d}}(\mathbf{G},\mathbf{X}). \end{align*} $$
$$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g): \mathscr{S}_{\mathsf{K}}^{\mathfrak{d}}(\mathbf{G},\mathbf{X})\to \mathscr{S}_{\mathsf{K}'}^{\mathfrak{d}}(\mathbf{G},\mathbf{X}). \end{align*} $$
-
(2) Writing
one has the following extension property relative to a characteristic
 $(0,p)$
discrete valuation ring R over
$(0,p)$
discrete valuation ring R over
 $\mathcal{O}_E$
: the natural map is a bijection.
$\mathcal{O}_E$
: the natural map is a bijection.
We will recall below, fairly precisely, the construction of the models
![]() $\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
. The superscript
$\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
. The superscript
![]() $\mathfrak {d}$
, which is either a parahoric Shimura datum of Hodge type well-adapted to
$\mathfrak {d}$
, which is either a parahoric Shimura datum of Hodge type well-adapted to
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
, or possibly
$(\mathbf {G},\mathbf {X},\mathcal{G})$
, or possibly
![]() $\varnothing $
when
$\varnothing $
when
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type. Its role is to emphasize various choices made in the construction of these models.
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type. Its role is to emphasize various choices made in the construction of these models.
3.2 The
 $\mathscr {A}$
-group and the
$\mathscr {A}$
-group and the
 $\mathscr {E}$
-group
$\mathscr {E}$
-group
Let
![]() ${\mathbf {G}}$
be a reductive
${\mathbf {G}}$
be a reductive
![]() $\mathbb {Q}$
-group. In this section we associate to
$\mathbb {Q}$
-group. In this section we associate to
![]() ${\mathbf {G}}$
groups
${\mathbf {G}}$
groups
![]() $\mathscr {A}({\mathbf {G}})$
and
$\mathscr {A}({\mathbf {G}})$
and
![]() $\mathscr {A}({\mathbf {G}})^\circ $
, and the so-called
$\mathscr {A}({\mathbf {G}})^\circ $
, and the so-called
![]() $\mathscr {E}$
-group to a parahoric Shimura datum, following [Reference DeligneDel79]. We also define analogs of these groups for
$\mathscr {E}$
-group to a parahoric Shimura datum, following [Reference DeligneDel79]. We also define analogs of these groups for
![]() $\mathbb {Z}_{(p)}$
-valued points following [Reference Kisin and PappasKP18] and [Reference Kisin and ZhouKZ21], and discuss some functorial properties of these groups. These groups play an important role in the construction of the models
$\mathbb {Z}_{(p)}$
-valued points following [Reference Kisin and PappasKP18] and [Reference Kisin and ZhouKZ21], and discuss some functorial properties of these groups. These groups play an important role in the construction of the models
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
from Theorem 3.9.
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
from Theorem 3.9.
The
 $\ast $
-product
$\ast $
-product
Let us begin by recalling the
![]() $\ast $
-product of Deligne (see [Reference DeligneDel79]).
$\ast $
-product of Deligne (see [Reference DeligneDel79]).
Suppose H and
![]() $\Gamma $
are abstract groups equipped with actions of a group
$\Gamma $
are abstract groups equipped with actions of a group
![]() $\Delta $
by group homomorphisms. Let
$\Delta $
by group homomorphisms. Let
be
![]() $\Delta $
-equivariant group homomorphisms, where
$\Delta $
-equivariant group homomorphisms, where
![]() $\Delta $
acts on itself by inner automorphisms, and assume that
$\Delta $
acts on itself by inner automorphisms, and assume that
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
are compatible in the sense that, for all
$\varphi $
are compatible in the sense that, for all
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma $
, we have the identity
$\Gamma $
, we have the identity
where
![]() $\cdot $
denotes the action of
$\cdot $
denotes the action of
![]() $\Delta $
on H. Then the semi-direct product
$\Delta $
on H. Then the semi-direct product
![]() $H \rtimes \Delta $
admits a quotient
$H \rtimes \Delta $
admits a quotient
where one easily checks that the subgroup
![]() $\{(\psi (\gamma ), \varphi (\gamma )^{-1})\}$
of all the elements of the form
$\{(\psi (\gamma ), \varphi (\gamma )^{-1})\}$
of all the elements of the form
![]() $(\psi (\gamma ), \varphi (\gamma )^{-1})$
for
$(\psi (\gamma ), \varphi (\gamma )^{-1})$
for
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma $
is a normal subgroup.
$\Gamma $
is a normal subgroup.
For the purposes of this section, we will refer to a datum
![]() $(H, \Gamma , \Delta , \psi , \varphi )$
as above as a tuple. A morphism of tuples
$(H, \Gamma , \Delta , \psi , \varphi )$
as above as a tuple. A morphism of tuples
![]() $(H, \Gamma , \Delta , \psi , \varphi ) \to (H', \Gamma ', \Delta ', \psi ', \varphi ')$
is a triple
$(H, \Gamma , \Delta , \psi , \varphi ) \to (H', \Gamma ', \Delta ', \psi ', \varphi ')$
is a triple
![]() $(f,g,h)$
, consisting of group homomorphisms
$(f,g,h)$
, consisting of group homomorphisms
![]() $f: H\to H'$
and
$f: H\to H'$
and
![]() $g: \Gamma \to \Gamma '$
equivariant relative to a group homomorphism
$g: \Gamma \to \Gamma '$
equivariant relative to a group homomorphism
![]() $h: \Delta \to \Delta '$
and such that
$h: \Delta \to \Delta '$
and such that
![]() $\psi ' \circ g = f \circ \psi $
and
$\psi ' \circ g = f \circ \psi $
and
![]() $h\circ \varphi = \varphi ' \circ f$
.
$h\circ \varphi = \varphi ' \circ f$
.
The
![]() $\ast $
-product satisfies the following elementary functoriality.
$\ast $
-product satisfies the following elementary functoriality.
Lemma 3.10. Any morphism of tuples
induces a homomorphism of groups
For future use, we also remark that if X is a set equipped with a right action of
![]() $H \rtimes \Delta $
, then the action descends to an action of
$H \rtimes \Delta $
, then the action descends to an action of
![]() $H \ast _\Gamma \Delta $
on the quotient
$H \ast _\Gamma \Delta $
on the quotient
![]() $X / \Gamma $
, where here
$X / \Gamma $
, where here
![]() $\Gamma $
acts on X via
$\Gamma $
acts on X via
The groups
 $\mathscr {A}({\mathbf {G}})$
and
$\mathscr {A}({\mathbf {G}})$
and
 $\mathscr {A}({\mathbf {G}})^\circ $
$\mathscr {A}({\mathbf {G}})^\circ $
Let us now recall some notation from [Reference DeligneDel79].
If
![]() ${\mathbf {G}}$
is a reductive group over
${\mathbf {G}}$
is a reductive group over
![]() $\mathbb {Q}$
, then we denote by
$\mathbb {Q}$
, then we denote by
![]() ${\mathbf {G}}(\mathbb {R})^+$
the connected component of the identity in
${\mathbf {G}}(\mathbb {R})^+$
the connected component of the identity in
![]() ${\mathbf {G}}(\mathbb {R})$
with respect to the real topology. For a subgroup
${\mathbf {G}}(\mathbb {R})$
with respect to the real topology. For a subgroup
![]() $\mathsf {H}$
of
$\mathsf {H}$
of
![]() ${\mathbf {G}}(\mathbb {R})$
, we denote by
${\mathbf {G}}(\mathbb {R})$
, we denote by
![]() $\mathsf {H}_+$
the inverse image of
$\mathsf {H}_+$
the inverse image of
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
in
${\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
in
![]() $\mathsf {H}$
. We write also
$\mathsf {H}$
. We write also
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+ = {\mathbf {G}}^{\text {ad}}(\mathbb {Q}) \cap {\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
.
${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+ = {\mathbf {G}}^{\text {ad}}(\mathbb {Q}) \cap {\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
.
Now suppose
![]() $(\mathbf {G},\mathbf {X})$
is a Shimura datum. Let
$(\mathbf {G},\mathbf {X})$
is a Shimura datum. Let
![]() $\mathbf {Z}$
denote the center of
$\mathbf {Z}$
denote the center of
![]() ${\mathbf {G}}$
, and let
${\mathbf {G}}$
, and let
![]() $\mathbf {Z}(\mathbb {Q})^-$
denote the closure of
$\mathbf {Z}(\mathbb {Q})^-$
denote the closure of
![]() $\mathbf {Z}(\mathbb {Q})$
in
$\mathbf {Z}(\mathbb {Q})$
in
![]() ${\mathbf {G}}(\mathbb {A}_f)$
. We define
${\mathbf {G}}(\mathbb {A}_f)$
. We define
where
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
acts by conjugation on
${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
acts by conjugation on
![]() ${\mathbf {G}}(\mathbb {A}_f) / \mathbf {Z}(\mathbb {Q})^-$
and
${\mathbf {G}}(\mathbb {A}_f) / \mathbf {Z}(\mathbb {Q})^-$
and
![]() ${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}(\mathbb {A}_f) / \mathbf {Z}(\mathbb {Q})^-$
and
${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}(\mathbb {A}_f) / \mathbf {Z}(\mathbb {Q})^-$
and
![]() ${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
are the obvious maps.
${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
are the obvious maps.
By [Reference MilneMil05, Proposition 5.1], the map
![]() ${\mathbf {G}}(\mathbb {R})^+ \to {\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
is surjective with kernel
${\mathbf {G}}(\mathbb {R})^+ \to {\mathbf {G}}^{\text {ad}}(\mathbb {R})^+$
is surjective with kernel
![]() $\mathbf {Z}(\mathbb {R}) \cap {\mathbf {G}}(\mathbb {R})^+$
, which is contained in the center of
$\mathbf {Z}(\mathbb {R}) \cap {\mathbf {G}}(\mathbb {R})^+$
, which is contained in the center of
![]() ${\mathbf {G}}(\mathbb {R})^+$
, so the conjugation action of
${\mathbf {G}}(\mathbb {R})^+$
, so the conjugation action of
![]() ${\mathbf {G}}$
on itself induces an action of
${\mathbf {G}}$
on itself induces an action of
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
on
${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
on
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})$
. Combining this with the action of
$\textrm {Sh}(\mathbf {G},\mathbf {X})$
. Combining this with the action of
![]() ${\mathbf {G}}(\mathbb {A}_f)$
on
${\mathbf {G}}(\mathbb {A}_f)$
on
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})$
determines a right action of
$\textrm {Sh}(\mathbf {G},\mathbf {X})$
determines a right action of
![]() $\mathscr {A}({\mathbf {G}})$
on
$\mathscr {A}({\mathbf {G}})$
on
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})$
.
$\textrm {Sh}(\mathbf {G},\mathbf {X})$
.
Denote by
![]() ${\mathbf {G}}(\mathbb {Q})_+^-$
the closure of
${\mathbf {G}}(\mathbb {Q})_+^-$
the closure of
![]() ${\mathbf {G}}(\mathbb {Q})_+$
in
${\mathbf {G}}(\mathbb {Q})_+$
in
![]() ${\mathbf {G}}(\mathbb {A}_f)$
. Define
${\mathbf {G}}(\mathbb {A}_f)$
. Define
where
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
acts by conjugation on
${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
acts by conjugation on
![]() ${\mathbf {G}}(\mathbb {Q})_+^- / \mathbf {Z}(\mathbb {Q})^-$
and
${\mathbf {G}}(\mathbb {Q})_+^- / \mathbf {Z}(\mathbb {Q})^-$
and
![]() ${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}(\mathbb {Q})_+^- / \mathbf {Z}(\mathbb {Q})^- $
and
${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}(\mathbb {Q})_+^- / \mathbf {Z}(\mathbb {Q})^- $
and
![]() ${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
are the obvious maps. Evidently
${\mathbf {G}}(\mathbb {Q})_+ / \mathbf {Z}(\mathbb {Q})\to {\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
are the obvious maps. Evidently
![]() $ \mathscr {A}({\mathbf {G}})^\circ $
is a subgroup of
$ \mathscr {A}({\mathbf {G}})^\circ $
is a subgroup of
![]() $\mathscr {A}({\mathbf {G}})$
. But, the group
$\mathscr {A}({\mathbf {G}})$
. But, the group
![]() $\mathscr {A}({\mathbf {G}})^\circ $
depends only on
$\mathscr {A}({\mathbf {G}})^\circ $
depends only on
![]() ${\mathbf {G}}^{\mathrm {der}}$
and not on
${\mathbf {G}}^{\mathrm {der}}$
and not on
![]() ${\mathbf {G}}$
, since by [Reference DeligneDel79, 2.1.15] it is given by the completion of
${\mathbf {G}}$
, since by [Reference DeligneDel79, 2.1.15] it is given by the completion of
![]() ${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
with respect to the topology whose open sets are images of congruence subgroups in
${\mathbf {G}}^{\text {ad}}(\mathbb {Q})^+$
with respect to the topology whose open sets are images of congruence subgroups in
![]() ${\mathbf {G}}^{\mathrm {der}}(\mathbb {Q})$
.
${\mathbf {G}}^{\mathrm {der}}(\mathbb {Q})$
.
It is clear that both the associations
![]() $\mathbf {G}\mapsto \mathscr {A}(\mathbf {G})$
and
$\mathbf {G}\mapsto \mathscr {A}(\mathbf {G})$
and
![]() $\mathbf {G}\mapsto \mathscr {A}(\mathbf {G})^\circ $
are functorial in maps of reductive groups
$\mathbf {G}\mapsto \mathscr {A}(\mathbf {G})^\circ $
are functorial in maps of reductive groups
![]() $f\colon \mathbf {G}\to \mathbf {H}$
such that
$f\colon \mathbf {G}\to \mathbf {H}$
such that
![]() $f(Z(\mathbf {G}))\subseteq Z(\mathbf {H})$
.
$f(Z(\mathbf {G}))\subseteq Z(\mathbf {H})$
.
The groups
 $\mathscr {A}(\boldsymbol{\mathcal{G}})$
and
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
and
 $\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
$\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
We define also analogs of
![]() $\mathscr {A}({\mathbf {G}})$
and
$\mathscr {A}({\mathbf {G}})$
and
![]() $\mathscr {A}({\mathbf {G}})^\circ $
for
$\mathscr {A}({\mathbf {G}})^\circ $
for
![]() $\mathbb {Z}_{(p)}$
-valued points, following [Reference Kisin and PappasKP18, §4.5.6] (see also [Reference Kisin and ZhouKZ21, §4.2.8]).
$\mathbb {Z}_{(p)}$
-valued points, following [Reference Kisin and PappasKP18, §4.5.6] (see also [Reference Kisin and ZhouKZ21, §4.2.8]).
To begin, we record the following well-known Beauville–Lazslo-type lemma (which is a basic case of [SP17, Tag 0F9Q]). For a ring A, let us denote by ![]() the category of finite type affine group A-schemes, and by
the category of finite type affine group A-schemes, and by
![]() $\mathbf {AlgGrp}^{\textrm {fl}}_A$
and
$\mathbf {AlgGrp}^{\textrm {fl}}_A$
and
![]() $\mathbf {AlgGrp}^{\textrm {sm}}_A$
the full subcategory of A-flat and A-smooth objects, respectively.
$\mathbf {AlgGrp}^{\textrm {sm}}_A$
the full subcategory of A-flat and A-smooth objects, respectively.
Proposition 3.11. Let R be a Noetherian ring and f a non-zerodivisor of R. Denote the f-adic completion of R by
![]() $\widehat {R}$
. Then the functor
$\widehat {R}$
. Then the functor
is an equivalence, where the target is the
![]() $2$
-fiber product (with the projection maps the obvious base change),
$2$
-fiber product (with the projection maps the obvious base change),
![]() $\theta _{\textrm {nat}}$
is the natural isomorphism, and
$\theta _{\textrm {nat}}$
is the natural isomorphism, and ![]() .
.
Suppose now that that
![]() $\mathbf {G}$
is a reductive group over
$\mathbf {G}$
is a reductive group over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $\mathcal{G}$
is a parahoric model of
$\mathcal{G}$
is a parahoric model of
![]() $\mathbf {G}_{\mathbb {Q}_p}$
. Let
$\mathbf {G}_{\mathbb {Q}_p}$
. Let
![]() $\mathcal{G}^{\text {ad}}$
denote the parahoric
$\mathcal{G}^{\text {ad}}$
denote the parahoric
![]() $\mathbb {Z}_p$
-model of
$\mathbb {Z}_p$
-model of
![]() $G^{\text {ad}}$
as discussed in §2.1. By Proposition 3.11 there exists a unique morphism of smooth group
$G^{\text {ad}}$
as discussed in §2.1. By Proposition 3.11 there exists a unique morphism of smooth group
![]() $\mathbb {Z}_{(p)}$
-schemes
$\mathbb {Z}_{(p)}$
-schemes
![]() $\boldsymbol{\mathcal{G}}\to \boldsymbol{\mathcal{G}}^{\textrm {ad}}$
modeling
$\boldsymbol{\mathcal{G}}\to \boldsymbol{\mathcal{G}}^{\textrm {ad}}$
modeling
![]() $\mathbf {G}\to \mathbf {G}^{\textrm {ad}}$
and
$\mathbf {G}\to \mathbf {G}^{\textrm {ad}}$
and
![]() $\mathcal{G}\to \mathcal{G}^{\textrm {ad}}$
. Let
$\mathcal{G}\to \mathcal{G}^{\textrm {ad}}$
. Let
![]() $\mathbf {Z}_{\mathbf {G}}$
denote the center of
$\mathbf {Z}_{\mathbf {G}}$
denote the center of
![]() ${\mathbf {G}}$
, and denote by
${\mathbf {G}}$
, and denote by
![]() $\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}$
the closure of
$\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}$
the closure of
![]() $\mathbf {Z}_{\mathbf {G}}$
in
$\mathbf {Z}_{\mathbf {G}}$
in
![]() $\boldsymbol{\mathcal{G}}$
.
$\boldsymbol{\mathcal{G}}$
.
Let
![]() $\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}(\mathbb {Z}_{(p)})^-$
and
$\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}(\mathbb {Z}_{(p)})^-$
and
![]() $\boldsymbol{\mathcal{G}}(\mathbb {Z}_{(p)})_+^-$
denote the closures of
$\boldsymbol{\mathcal{G}}(\mathbb {Z}_{(p)})_+^-$
denote the closures of
![]() $\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}(\mathbb {Z}_{(p)})$
and
$\boldsymbol{\mathcal{Z}}_{{\mathbf {G}}}(\mathbb {Z}_{(p)})$
and
![]() $\boldsymbol{\mathcal{G}}(\mathbb {Z}_{(p)})_+$
in
$\boldsymbol{\mathcal{G}}(\mathbb {Z}_{(p)})_+$
in
![]() ${\mathbf {G}}(\mathbb {A}_f^p)$
, respectively. Following [Reference Kisin and PappasKP18, §4.5.6] and [Reference Kisin and ZhouKZ21, §4.2.8], we set
${\mathbf {G}}(\mathbb {A}_f^p)$
, respectively. Following [Reference Kisin and PappasKP18, §4.5.6] and [Reference Kisin and ZhouKZ21, §4.2.8], we set
and
where in the first definition we have that
![]() $\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+$
acts on
$\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+$
acts on
![]() ${\mathbf {G}}(\mathbb {A}_f^p)/\boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^-$
by conjugation and
${\mathbf {G}}(\mathbb {A}_f^p)/\boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^-$
by conjugation and
are the obvious maps, and similarly for the second definition.
By [Reference Kisin and PappasKP18, Lemma 4.6.4 (2)],
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
is a subgroup of
$\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
is a subgroup of
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
but depends only on
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
but depends only on
![]() $\boldsymbol{\mathcal{G}}^{\mathrm {der}}$
, where
$\boldsymbol{\mathcal{G}}^{\mathrm {der}}$
, where
![]() $\mathcal{G}^{\mathrm {der}}$
denotes the parahoric model of
$\mathcal{G}^{\mathrm {der}}$
denotes the parahoric model of
![]() $\mathbf {G}_{\mathbb {Q}_p}^{\mathrm {der}}$
obtained as in §2.1 and
$\mathbf {G}_{\mathbb {Q}_p}^{\mathrm {der}}$
obtained as in §2.1 and
![]() $\boldsymbol{\mathcal{G}}^{\mathrm {der}}$
is obtained from Proposition 3.11.
$\boldsymbol{\mathcal{G}}^{\mathrm {der}}$
is obtained from Proposition 3.11.
Lemma 3.12. Let
![]() ${\mathbf {G}}$
and
${\mathbf {G}}$
and
![]() $\mathbf {H}$
be reductive groups over
$\mathbf {H}$
be reductive groups over
![]() $\mathbb {Q}$
and set
$\mathbb {Q}$
and set
![]() $G=\mathbf {G}_{\mathbb {Q}_p}$
and
$G=\mathbf {G}_{\mathbb {Q}_p}$
and
![]() $H=\mathbf {H}_{\mathbb {Q}_p}$
. Fix parahoric models
$H=\mathbf {H}_{\mathbb {Q}_p}$
. Fix parahoric models
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $\mathcal{H}$
of G and H corresponding to points x and y in the buildings
$\mathcal{H}$
of G and H corresponding to points x and y in the buildings
![]() $\mathscr {B}(G,\mathbb {Q}_p)$
and
$\mathscr {B}(G,\mathbb {Q}_p)$
and
![]() $\mathscr {B}(H,\mathbb {Q}_p)$
, respectively. Suppose
$\mathscr {B}(H,\mathbb {Q}_p)$
, respectively. Suppose
![]() $f: {\mathbf {G}} \to \mathbf {H}$
is a homomorphism of reductive
$f: {\mathbf {G}} \to \mathbf {H}$
is a homomorphism of reductive
![]() $\mathbb {Q}$
-groups carrying
$\mathbb {Q}$
-groups carrying
![]() $\mathbf {Z}_{\mathbf {G}}$
into
$\mathbf {Z}_{\mathbf {G}}$
into
![]() $\mathbf {Z}_{\mathbf {H}}$
, and suppose that
$\mathbf {Z}_{\mathbf {H}}$
, and suppose that
is a map of buildings which is equivariant for the map
![]() $f: G(\mathbb {Q}_p^{\textrm {ur}}) \to H(\mathbb {Q}_p^{\textrm {ur}})$
and which sends x to y. Then f induces group homomorphisms
$f: G(\mathbb {Q}_p^{\textrm {ur}}) \to H(\mathbb {Q}_p^{\textrm {ur}})$
and which sends x to y. Then f induces group homomorphisms
Proof. Since f carries
![]() $\mathbf {Z}_{\mathbf {G}}$
into
$\mathbf {Z}_{\mathbf {G}}$
into
![]() $\mathbf {Z}_{\mathbf {H}}$
, it follows that f induces a homomorphism of groups
$\mathbf {Z}_{\mathbf {H}}$
, it follows that f induces a homomorphism of groups
The equivariance of
![]() $f_\ast $
implies that
$f_\ast $
implies that
![]() $f(\operatorname {Stab}_{G(\mathbb {Q}_p^{\textrm {ur}})}(x)) \subseteq \operatorname {Stab}_{H(\mathbb {Q}_p^{\textrm {ur}})}(y)$
, and hence that
$f(\operatorname {Stab}_{G(\mathbb {Q}_p^{\textrm {ur}})}(x)) \subseteq \operatorname {Stab}_{H(\mathbb {Q}_p^{\textrm {ur}})}(y)$
, and hence that
![]() ${f(\mathcal{G}(\mathbb {Z}_p^{\textrm {ur}}))\subseteq \mathcal{H}(\mathbb {Z}_p^{\textrm {ur}})}$
. Thus f extends to a morphism
${f(\mathcal{G}(\mathbb {Z}_p^{\textrm {ur}}))\subseteq \mathcal{H}(\mathbb {Z}_p^{\textrm {ur}})}$
. Thus f extends to a morphism
![]() $f: \mathcal{G} \to \mathcal{H}$
by [Reference Kaletha and PrasadKP23, Corollary 2.10.10]. We similarly obtain an extension
$f: \mathcal{G} \to \mathcal{H}$
by [Reference Kaletha and PrasadKP23, Corollary 2.10.10]. We similarly obtain an extension
![]() $f^{\text {ad}}: \mathcal{G}^{\text {ad}} \to \mathcal{H}^{\text {ad}}$
of
$f^{\text {ad}}: \mathcal{G}^{\text {ad}} \to \mathcal{H}^{\text {ad}}$
of
![]() $f^{\text {ad}}:G^{\text {ad}} \to H^{\text {ad}}$
, which induces
$f^{\text {ad}}:G^{\text {ad}} \to H^{\text {ad}}$
, which induces
Moreover, as f extends to a morphism
![]() $\mathcal{G} \to \mathcal{H}$
, it follows that f restricts to homomorphisms
$\mathcal{G} \to \mathcal{H}$
, it follows that f restricts to homomorphisms
and
By Lemma 3.10, it remains only to check that
![]() $(f, f', f^{\text {ad}})$
and
$(f, f', f^{\text {ad}})$
and
![]() $(f^\circ , f', f^{\text {ad}})$
induce morphisms of tuples. By uniqueness of the extension of
$(f^\circ , f', f^{\text {ad}})$
induce morphisms of tuples. By uniqueness of the extension of
![]() $G \to H \to H^{\text {ad}}$
to parahoric models and equivariance of the bijections
$G \to H \to H^{\text {ad}}$
to parahoric models and equivariance of the bijections ![]() and
and ![]() from Lemma 2.5, we see that the diagram
from Lemma 2.5, we see that the diagram

commutes. Thus it remains only to show that f is equivariant for the action of
![]() $\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+$
. But this is clear since the action of
$\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+$
. But this is clear since the action of
![]() $\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+ \subseteq \mathbf {G}(\mathbb {Q})$
on
$\boldsymbol{\mathcal{G}}^{\text {ad}}(\mathbb {Z}_{(p)})^+ \subseteq \mathbf {G}(\mathbb {Q})$
on
![]() $\mathbf {G}(\mathbb {A}_f^p)/\boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^-$
is via conjugation, and
$\mathbf {G}(\mathbb {A}_f^p)/\boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^-$
is via conjugation, and
![]() $f\colon {\mathbf {G}}(\mathbb {A}_f^p)/ \boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^- \to \mathbf {H}(\mathbb {A}_f^p)/ \boldsymbol{\mathcal{Z}}_{\mathbf {H}}(\mathbb {Z}_{(p)})^-$
is a group homomorphism.
$f\colon {\mathbf {G}}(\mathbb {A}_f^p)/ \boldsymbol{\mathcal{Z}}_{\mathbf {G}}(\mathbb {Z}_{(p)})^- \to \mathbf {H}(\mathbb {A}_f^p)/ \boldsymbol{\mathcal{Z}}_{\mathbf {H}}(\mathbb {Z}_{(p)})^-$
is a group homomorphism.
The group
 $\mathscr {E}(\boldsymbol{\mathcal{G}})$
$\mathscr {E}(\boldsymbol{\mathcal{G}})$
Suppose now that
![]() $(\mathbf {G},\mathbf {X}, \mathcal{G})$
is a parahoric Shimura datum with reflex field
$(\mathbf {G},\mathbf {X}, \mathcal{G})$
is a parahoric Shimura datum with reflex field
![]() $\mathbf {E}$
. Let
$\mathbf {E}$
. Let
![]() $\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
. Fix a connected component
$\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
. Fix a connected component
![]() $\mathbf {X}^+$
of
$\mathbf {X}^+$
of
![]() $\mathbf {X}$
, which determines connected Shimura varieties
$\mathbf {X}$
, which determines connected Shimura varieties
![]() $\textrm {Sh}(\mathbf {G},\mathbf {X})^+ \subseteq \textrm {Sh}(\mathbf {G},\mathbf {X})$
and
$\textrm {Sh}(\mathbf {G},\mathbf {X})^+ \subseteq \textrm {Sh}(\mathbf {G},\mathbf {X})$
and
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+ \subseteq \textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})$
.
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+ \subseteq \textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})$
.
By Lemma 3.2, the action of
![]() $\text {Gal}(\overline {{\mathbf {E}}}/ {\mathbf {E}})$
on
$\text {Gal}(\overline {{\mathbf {E}}}/ {\mathbf {E}})$
on
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+$
factors through
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+$
factors through
![]() $\text {Gal}({\mathbf {E}}^p/ {\mathbf {E}})$
. By abuse of notation, we will use
$\text {Gal}({\mathbf {E}}^p/ {\mathbf {E}})$
. By abuse of notation, we will use
![]() $\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})^+$
to refer to the
$\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})^+$
to refer to the
![]() ${\mathbf {E}}^p$
-scheme obtained by descent.
${\mathbf {E}}^p$
-scheme obtained by descent.
Let
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}}) \subseteq \mathscr {A}(\boldsymbol{\mathcal{G}}) \times \text {Gal}({\mathbf {E}}^p / {\mathbf {E}})$
denote the stabilizer of
$\mathscr {E}(\boldsymbol{\mathcal{G}}) \subseteq \mathscr {A}(\boldsymbol{\mathcal{G}}) \times \text {Gal}({\mathbf {E}}^p / {\mathbf {E}})$
denote the stabilizer of
![]() $\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})^+$
in
$\textrm {Sh}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})^+$
in
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})$
. By [Reference Kisin and PappasKP18, Lemma 4.6.6],
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})$
. By [Reference Kisin and PappasKP18, Lemma 4.6.6],
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}})$
is an extension of
$\mathscr {E}(\boldsymbol{\mathcal{G}})$
is an extension of
![]() $\text {Gal}({\mathbf {E}}^p/{\mathbf {E}})$
by
$\text {Gal}({\mathbf {E}}^p/{\mathbf {E}})$
by
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
, and there is a canonical isomorphism
$\mathscr {A}(\boldsymbol{\mathcal{G}})^\circ $
, and there is a canonical isomorphism
where an element of
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}})$
acts on
$\mathscr {E}(\boldsymbol{\mathcal{G}})$
acts on
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
via conjugation by its image in
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
via conjugation by its image in
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
.Footnote
6
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
.Footnote
6
The
![]() $\mathscr {E}$
-group satisfies a functoriality akin to that of the
$\mathscr {E}$
-group satisfies a functoriality akin to that of the
![]() $\mathscr {A}$
-groups.
$\mathscr {A}$
-groups.
Lemma 3.13. Let
![]() $f: (\mathbf {G}_1, \mathbf {X}_1,\mathcal{G}_1) \to (\mathbf {G}, \mathbf {X}, \mathcal{G})$
be a morphism of parahoric Shimura data. Suppose
$f: (\mathbf {G}_1, \mathbf {X}_1,\mathcal{G}_1) \to (\mathbf {G}, \mathbf {X}, \mathcal{G})$
be a morphism of parahoric Shimura data. Suppose
![]() $\mathcal{G}_1$
and
$\mathcal{G}_1$
and
![]() $\mathcal{G}$
correspond to points
$\mathcal{G}$
correspond to points
![]() $x_1$
and x in the buildings
$x_1$
and x in the buildings
![]() $\mathscr {B}(G_1, \mathbb {Q}_p)$
and
$\mathscr {B}(G_1, \mathbb {Q}_p)$
and
![]() $\mathscr {B}(G,\mathbb {Q}_p)$
, respectively. Suppose the induced
$\mathscr {B}(G,\mathbb {Q}_p)$
, respectively. Suppose the induced
![]() $f: \mathbf {G}_1 \to \mathbf {G}$
carries
$f: \mathbf {G}_1 \to \mathbf {G}$
carries
![]() $\mathbf {Z}_{\mathbf {G}}$
into
$\mathbf {Z}_{\mathbf {G}}$
into
![]() $\mathbf {Z}_{\mathbf {H}}$
, and suppose that
$\mathbf {Z}_{\mathbf {H}}$
, and suppose that
is a map of buildings which is equivariant for the map
![]() $f\colon G_1(\mathbb {Q}_p^{\textrm {ur}}) \to G(\mathbb {Q}_p^{\textrm {ur}})$
and which sends
$f\colon G_1(\mathbb {Q}_p^{\textrm {ur}}) \to G(\mathbb {Q}_p^{\textrm {ur}})$
and which sends
![]() $x_1$
to x. Then f induces a group homomorphism
$x_1$
to x. Then f induces a group homomorphism
Proof. This follows from the definition of
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}})$
by Lemma 3.12, along with the fact that f is a morphism of Shimura data.
$\mathscr {E}(\boldsymbol{\mathcal{G}})$
by Lemma 3.12, along with the fact that f is a morphism of Shimura data.
Suppose now we have two parahoric Shimura data
![]() $(\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
and
$(\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
and
![]() $(\mathbf {G}, \mathbf {X}, \mathcal{G})$
, and that there is a central isogeny
$(\mathbf {G}, \mathbf {X}, \mathcal{G})$
, and that there is a central isogeny
![]() $\alpha \colon \mathbf {G}_1^{\mathrm {der}} \to \mathbf {G}^{\mathrm {der}}$
which induces an isomorphism of Shimura data
$\alpha \colon \mathbf {G}_1^{\mathrm {der}} \to \mathbf {G}^{\mathrm {der}}$
which induces an isomorphism of Shimura data
Let
![]() $x_1$
in
$x_1$
in
![]() $\mathscr {B}(G_1, \mathbb {Q}_p)$
and x in
$\mathscr {B}(G_1, \mathbb {Q}_p)$
and x in
![]() $\mathscr {B}(G,\mathbb {Q}_p)$
denote points in the buildings of
$\mathscr {B}(G,\mathbb {Q}_p)$
denote points in the buildings of
![]() $G_1$
and G, respectively, which correspond to
$G_1$
and G, respectively, which correspond to
![]() $\mathcal{G}_1$
and
$\mathcal{G}_1$
and
![]() $\mathcal{G}$
. Let us further assume that
$\mathcal{G}$
. Let us further assume that
![]() $x_1$
and x correspond to the same point
$x_1$
and x correspond to the same point
![]() $x_1^{\text {ad}} = x^{\text {ad}}$
in the building
$x_1^{\text {ad}} = x^{\text {ad}}$
in the building
![]() $\mathscr {B}(G_1^{\text {ad}}, \mathbb {Q}_p) \simeq \mathscr {B}(G^{\text {ad}}, \mathbb {Q}_p)$
.
$\mathscr {B}(G_1^{\text {ad}}, \mathbb {Q}_p) \simeq \mathscr {B}(G^{\text {ad}}, \mathbb {Q}_p)$
.
Fix a connected component
![]() $\mathbf {X}_1^+$
as above, which determines a group
$\mathbf {X}_1^+$
as above, which determines a group
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}}_1)$
. By the real approximation theorem, we may assume that the image of
$\mathscr {E}(\boldsymbol{\mathcal{G}}_1)$
. By the real approximation theorem, we may assume that the image of
![]() $\mathbf {X} \subseteq \mathbf {X}^{\text {ad}}$
contains
$\mathbf {X} \subseteq \mathbf {X}^{\text {ad}}$
contains
![]() $\mathbf {X}_1^+$
by replacing
$\mathbf {X}_1^+$
by replacing
![]() $\mathbf {X}$
by its conjugate by some element of
$\mathbf {X}$
by its conjugate by some element of
![]() $\mathbf {G}^{\text {ad}}(\mathbb {Q})$
. We set
$\mathbf {G}^{\text {ad}}(\mathbb {Q})$
. We set
![]() $\mathbf {E}' = \mathbf {E}_1\mathbf {E}$
, and define
$\mathbf {E}' = \mathbf {E}_1\mathbf {E}$
, and define
![]() $\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
to be the fiber product
$\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
to be the fiber product
Then
![]() $\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
is an extension of
$\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
is an extension of
![]() $\text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E}')$
by
$\text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E}')$
by
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ $
, and by [Reference Kisin and PappasKP18, Lemma 4.6.9], there is a natural map of extensions
$\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ $
, and by [Reference Kisin and PappasKP18, Lemma 4.6.9], there is a natural map of extensions
In particular, it follows that there is an isomorphism
3.3 Construction of Kisin–Pappas–Zhou models
We now briefly recall the construction of the Kisin–Pappas–Zhou models
![]() $\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
from Theorem 3.9, focusing on the aspects most relevant for our purposes. We encourage the reader to consult the relevant parts of [Reference Kisin and PappasKP18], [Reference Kisin and ZhouKZ21], and [Reference Kisin, Pappas and ZhouKPZ24] for details.
$\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
from Theorem 3.9, focusing on the aspects most relevant for our purposes. We encourage the reader to consult the relevant parts of [Reference Kisin and PappasKP18], [Reference Kisin and ZhouKZ21], and [Reference Kisin, Pappas and ZhouKPZ24] for details.
Throughout this section we fix the following data/notation:

We refer to §2.1 and §3.2 for the meaning of these terms, as well as other notation related to Bruhat–Tits theory and Shimura varieties.
The construction of Kisin–Pappas–Zhou models is carried out in a four step process.
Step 1: Global construction for Siegel type
Suppose that
![]() $(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
is a Siegel datum. Choose a
$(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
is a Siegel datum. Choose a
![]() $\mathbb {Z}_p$
-lattice
$\mathbb {Z}_p$
-lattice
![]() $\Lambda \subseteq \mathbf {V}_{\mathbb {Q}_p}$
and set
$\Lambda \subseteq \mathbf {V}_{\mathbb {Q}_p}$
and set
For
![]() $\mathsf {K}^p$
a neat compact open subgroups of
$\mathsf {K}^p$
a neat compact open subgroups of
![]() $\textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}}\mathbb {A}^f_p)$
, we set
$\textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}}\mathbb {A}^f_p)$
, we set
![]() ${\pmb {\mathscr {S}}}_{\mathsf {K}_p\mathsf { K}^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
to be the
${\pmb {\mathscr {S}}}_{\mathsf {K}_p\mathsf { K}^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
to be the
![]() $\mathbb {Z}_{(p)}$
-scheme given by Mumford’s moduli of principally polarized abelian varieties with
$\mathbb {Z}_{(p)}$
-scheme given by Mumford’s moduli of principally polarized abelian varieties with
![]() $\mathsf {K}^p$
-level structure (see [Reference DeligneDel79, §4]). These form a
$\mathsf {K}^p$
-level structure (see [Reference DeligneDel79, §4]). These form a
![]() $\textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}} \mathbb {A}_f^p)$
-system of
$\textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}} \mathbb {A}_f^p)$
-system of
![]() $\mathbb {Z}_{(p)}$
-schemes.
$\mathbb {Z}_{(p)}$
-schemes.
Step 2: Construction for Hodge type data
Let us now assume that
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Hodge type datum and let us fix a parahoric Hodge embedding
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Hodge type datum and let us fix a parahoric Hodge embedding
which respects stabilizers. As in [Reference KisinKis10, Lemma 2.10] we may choose a neat compact open subgroup
![]() $\mathsf {K}_1^p\subseteq \mathbf {GSp}(\mathbf {V}\otimes _{\mathbb {Q}}\mathbb {A}_f^p)$
such that
$\mathsf {K}_1^p\subseteq \mathbf {GSp}(\mathbf {V}\otimes _{\mathbb {Q}}\mathbb {A}_f^p)$
such that
![]() $\iota (\widetilde {\mathsf {K}}_p\mathsf {K}^p)\subseteq \textrm {GSp}(\Lambda )\mathsf {K}^p_1$
, and such that the map
$\iota (\widetilde {\mathsf {K}}_p\mathsf {K}^p)\subseteq \textrm {GSp}(\Lambda )\mathsf {K}^p_1$
, and such that the map
is a closed embedding.
We then set
-
⋄
 to be the normalization of the Zariski closure of
to be the normalization of the Zariski closure of
 $\textrm {Sh}_{\widetilde {\mathsf {K}}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
in the scheme
$\textrm {Sh}_{\widetilde {\mathsf {K}}_p\mathsf {K}^p}(\mathbf {G},\mathbf {X})$
in the scheme
 ${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf {K}_1^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )_{\mathcal{O}_{(v)}}$
, via the embedding in (3.6),
${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf {K}_1^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )_{\mathcal{O}_{(v)}}$
, via the embedding in (3.6), -
⋄
 to be the normalization (in the sense of [SP17, Tag 0BAK]) of
to be the normalization (in the sense of [SP17, Tag 0BAK]) of  relative to finite map
relative to finite map  $$ \begin{align*} \textrm{Sh}_{\mathsf{K}_p\mathsf{K}^p}(\mathbf{G},\mathbf{X})\to \textrm{Sh}_{\widetilde{\mathsf{K}}_p\mathsf{K}^p}(\mathbf{G},\mathbf{X}). \end{align*} $$
$$ \begin{align*} \textrm{Sh}_{\mathsf{K}_p\mathsf{K}^p}(\mathbf{G},\mathbf{X})\to \textrm{Sh}_{\widetilde{\mathsf{K}}_p\mathsf{K}^p}(\mathbf{G},\mathbf{X}). \end{align*} $$
Remark 3.14. As each
![]() ${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf {K}_1^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )_{\mathcal{O}_{(v)}}$
is quasi-projective over
${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf {K}_1^p}(\textrm {GSp}(\mathbf {V}),\mathfrak {h}^\pm )_{\mathcal{O}_{(v)}}$
is quasi-projective over
![]() $\mathbb {Z}_{(p)}$
(see [Reference Mumford, Fogarty and KirwanMFK94, Theorem 7.9]), Zariski closed embeddings are quasi-projective, normalization maps are finite in our setting (see [SP17, Tag 035R] and [SP17, Tag 07QW]) and thus quasi-projective, we deduce that each
$\mathbb {Z}_{(p)}$
(see [Reference Mumford, Fogarty and KirwanMFK94, Theorem 7.9]), Zariski closed embeddings are quasi-projective, normalization maps are finite in our setting (see [SP17, Tag 035R] and [SP17, Tag 07QW]) and thus quasi-projective, we deduce that each ![]() is a quasi-projective
is a quasi-projective
![]() $\mathcal{O}_{(v)}$
-scheme.
$\mathcal{O}_{(v)}$
-scheme.
As Zariski closure and normalization are functorial constructions, we see that ![]() form a projective system. We then further set
form a projective system. We then further set
The continuous
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-action of
$\mathbf {G}(\mathbb {A}_f^p)$
-action of
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_E$
extends to a continuous action on
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_E$
extends to a continuous action on ![]() with the property that
with the property that
compatibly in
![]() $\mathsf {K}^p$
. We finally set
$\mathsf {K}^p$
. We finally set
which is a scheme over
![]() $\mathcal{O}_v$
with
$\mathcal{O}_v$
with
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-action and a scheme over
$\mathbf {G}(\mathbb {A}_f^p)$
-action and a scheme over
![]() $\mathcal{O}_v$
, respectively.
$\mathcal{O}_v$
, respectively.
A priori, these schemes depend on the choice of parahoric Hodge embedding which respects stabilizers. That said, the following shows that this not the case, thus justifying the omission of the parahoric Hodge embedding from the notation.
Proposition 3.15 ([Reference Pappas and RapoportPR24, Theorem 4.5.2] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b]).
The objects ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are canonically independent of parahoric Hodge embedding.
are canonically independent of parahoric Hodge embedding.
While the action of
![]() $\mathbf {G}(\mathbb {A}_f^p)$
extends to actions on
$\mathbf {G}(\mathbb {A}_f^p)$
extends to actions on ![]() and
and ![]() , it is not a priori clear that these can be extended further to actions of
, it is not a priori clear that these can be extended further to actions of
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
. That said, this does hold true when
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
. That said, this does hold true when
![]() $Z(G_1)$
is R-smooth, as explained in [Reference Kisin, Pappas and ZhouKPZ24, Proof of Proposition 7.1.14].Footnote
7
$Z(G_1)$
is R-smooth, as explained in [Reference Kisin, Pappas and ZhouKPZ24, Proof of Proposition 7.1.14].Footnote
7
Step 3: Global construction relative to a well-adapted Hodge type datum
Continue to assume
![]() $p>2$
, and suppose that
$p>2$
, and suppose that
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. The key proposition which allows us to bootstrap from the previous cases is the following.
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. The key proposition which allows us to bootstrap from the previous cases is the following.
Proposition 3.16 ([Reference Kisin, Pappas and ZhouKPZ24, Proposition 7.2.18]).
There exists a parahoric Shimura datum
![]() $(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
of Hodge type well-adapted to
$(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
of Hodge type well-adapted to
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
with the property that
$(\mathbf {G},\mathbf {X},\mathcal{G})$
with the property that
![]() $Z(G_1)$
is an R-smooth torus.
$Z(G_1)$
is an R-smooth torus.
Throughout the remainder of this section, we fix
![]() $(\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
as in the proposition above. Choose connected components
$(\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
as in the proposition above. Choose connected components
![]() $\mathbf {X}^+ \subseteq \mathbf {X}$
and
$\mathbf {X}^+ \subseteq \mathbf {X}$
and
![]() $\mathbf {X}_1^+\subseteq \mathbf {X}_1$
which correspond in
$\mathbf {X}_1^+\subseteq \mathbf {X}_1$
which correspond in
![]() $\mathbf {X}^{\textrm {ad}}\simeq \mathbf {X}_1^{\textrm {ad}}$
. Using Lemma 3.2, we obtain connected components
$\mathbf {X}^{\textrm {ad}}\simeq \mathbf {X}_1^{\textrm {ad}}$
. Using Lemma 3.2, we obtain connected components
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+$
and
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})^+$
and
![]() $\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)^+$
defined over
$\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)^+$
defined over
![]() $\mathbf {E}^p$
and
$\mathbf {E}^p$
and
![]() $\mathbf {E}_1^p$
, respectively. We also obtain subgroups
$\mathbf {E}_1^p$
, respectively. We also obtain subgroups
and the group
as defined in §3.2.
We have a bijection
as follows from combining the following general results.
Lemma 3.17. Let
![]() $\{S_i\}$
be a projective system of spectral spaces with quasi-compact surjective transition maps. Write
$\{S_i\}$
be a projective system of spectral spaces with quasi-compact surjective transition maps. Write
![]() $S=\varprojlim S_i$
. Then,
$S=\varprojlim S_i$
. Then,
-
(1) S is a spectral space,
-
(2) the (dense) quasi-compact open subsets of S are precisely those of the form
 $U=\varprojlim U_i$
with each
$U=\varprojlim U_i$
with each
 $U_i\subseteq S_i$
a (dense) quasi-compact open subset such that
$U_i\subseteq S_i$
a (dense) quasi-compact open subset such that
 $U_i$
is the preimage of
$U_i$
is the preimage of
 $U_j$
under
$U_j$
under
 $S_i\to S_j$
,
$S_i\to S_j$
, -
(3) the natural map
 $\pi _0(S)\to \pi _0(S_i)$
is surjective for all i,
$\pi _0(S)\to \pi _0(S_i)$
is surjective for all i, -
(4) the natural map
 $\pi _0(S)\to \lim \pi _0(S_i)$
is a homeomorphism.
$\pi _0(S)\to \lim \pi _0(S_i)$
is a homeomorphism.
Moreover, if each
![]() $S_i$
is a disjoint union of finitely many irreducible spaces, then for every dense quasi-compact open
$S_i$
is a disjoint union of finitely many irreducible spaces, then for every dense quasi-compact open
![]() $U\subseteq S$
the natural map
$U\subseteq S$
the natural map
![]() $\pi _0(U)\to \pi _0(S)$
is a homeomorphism.
$\pi _0(U)\to \pi _0(S)$
is a homeomorphism.
Proof. Claim (1) follows from [Reference Fujiwara and KatoFK18, Chapter 0, Theorem 2.2.10]. Claim (2) follows from [Reference Fujiwara and KatoFK18, Chapter 0, Proposition 2.2.9 and Lemma 2.2.19]. Claim (4) follows from [Reference Achinger, Lara and YoucisALY21, Lemma 4.1.6]), and claim (3) then follows from claim (4), as each projection
![]() $\pi _0(S_i)\to \pi _0(S_j)$
is a surjection of compact Hausdorff spaces (see [SP17, Tag 0906]), and so
$\pi _0(S_i)\to \pi _0(S_j)$
is a surjection of compact Hausdorff spaces (see [SP17, Tag 0906]), and so
![]() $\varprojlim \pi _0(S_i)\to \pi _0(S_i)$
is surjective by Tychonoff’s theorem. For the final claim write
$\varprojlim \pi _0(S_i)\to \pi _0(S_i)$
is surjective by Tychonoff’s theorem. For the final claim write
![]() $U=\varprojlim U_i$
with
$U=\varprojlim U_i$
with
![]() $U_i\subseteq S_i$
a dense quasi-compact open. Then, each
$U_i\subseteq S_i$
a dense quasi-compact open. Then, each
![]() $\pi _0(U_i)\to \pi _0(S_i)$
is clearly a bijection, and so the claim follows by passing to the limit using (4).
$\pi _0(U_i)\to \pi _0(S_i)$
is clearly a bijection, and so the claim follows by passing to the limit using (4).
Lemma 3.18. Let
![]() $X\to Y$
be a flat and finite type morphism of Noetherian schemes where X is normal. Then, X is a finite disjoint union of irreducible spaces, and for any dense open
$X\to Y$
be a flat and finite type morphism of Noetherian schemes where X is normal. Then, X is a finite disjoint union of irreducible spaces, and for any dense open
![]() $U\subseteq Y$
, the open
$U\subseteq Y$
, the open
![]() $X_U\subseteq X$
is dense.
$X_U\subseteq X$
is dense.
Proof. The first claim follows from [SP17, Tag 033N], and the latter is clear as f is open by [SP17, Tag 01UA].
The bijection (3.7) shows that
![]() $\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)^+$
corresponds uniquely to a connected component
$\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)^+$
corresponds uniquely to a connected component ![]() of
of ![]() . Set
. Set
![]() $\mathcal{O}^{\prime p}_{(v)}=\mathcal{O}_{\mathbf {E}^{\prime p} } \otimes _{\mathcal{O}_{\mathbf {E}}}\mathcal{O}_{(v)}$
. Consider then
$\mathcal{O}^{\prime p}_{(v)}=\mathcal{O}_{\mathbf {E}^{\prime p} } \otimes _{\mathcal{O}_{\mathbf {E}}}\mathcal{O}_{(v)}$
. Consider then
As observed in Step 2, we have that the right
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}}_1)$
-action extends to
$\mathscr {A}(\boldsymbol{\mathcal{G}}_1)$
-action extends to ![]() and by the bijection (3.7) we deduce that
and by the bijection (3.7) we deduce that
![]() $\mathscr {E}(\boldsymbol{\mathcal{G}}_1)$
stabilizes
$\mathscr {E}(\boldsymbol{\mathcal{G}}_1)$
stabilizes ![]() . We then get an induced action of
. We then get an induced action of
![]() $\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
on
$\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
on ![]() . We then finally let
. We then finally let
![]() $\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
act on the right of (3.8) by setting
$\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
act on the right of (3.8) by setting
where
![]() $\overline {e}$
denotes the image of e under the homomorphisms
$\overline {e}$
denotes the image of e under the homomorphisms
where the first map is as in (3.4), and the second map is projection.
We then consider
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})\rtimes \mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
, where
$\mathscr {A}(\boldsymbol{\mathcal{G}})\rtimes \mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
, where
![]() $\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
acts again via the homomorphism from (3.10). Let the semi-direct product
$\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
acts again via the homomorphism from (3.10). Let the semi-direct product
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})\rtimes \mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
act on (3.8) by having
$\mathscr {A}(\boldsymbol{\mathcal{G}})\rtimes \mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
act on (3.8) by having
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
act by right multiplication on the
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
act by right multiplication on the
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
-factor of (3.8), i.e.,
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
-factor of (3.8), i.e.,
As in (3.2) we obtain an action of
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})\ast _{\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ }\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
on
$\mathscr {A}(\boldsymbol{\mathcal{G}})\ast _{\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ }\mathscr {E}_{\mathbf {E}'}(\boldsymbol{\mathcal{G}}_1)$
on

with notation as in loc. cit. Since
(see (3.5)), we obtain an action of
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
, and hence of
$\mathscr {A}(\boldsymbol{\mathcal{G}})\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
, and hence of
![]() $\mathbf {G}(\mathbb {A}_f^p)\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
, on (3.12).
$\mathbf {G}(\mathbb {A}_f^p)\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
, on (3.12).
Now, let
![]() $J\subset G(\mathbb {Q}_p)$
denote a set of coset representatives for the image of the natural map
$J\subset G(\mathbb {Q}_p)$
denote a set of coset representatives for the image of the natural map
where the map
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ \to \mathscr {A}(\boldsymbol{\mathcal{G}})$
is as in Lemma 3.12. Then J is finite. Let
$\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ \to \mathscr {A}(\boldsymbol{\mathcal{G}})$
is as in Lemma 3.12. Then J is finite. Let
![]() $\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
, and consider
$\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
, and consider

which we endow with the factor-wise (relative to the J-indexed factors) action of the group
![]() $\mathbf {G}(\mathbb {A}_f^p)\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
. This action is continuous, and so by Galois descent gives rise to a unique scheme
$\mathbf {G}(\mathbb {A}_f^p)\times \text {Gal}(\mathbf {E}^{\prime p}/\mathbf {E})$
. This action is continuous, and so by Galois descent gives rise to a unique scheme
![]() ${\pmb {\mathscr {S}}}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{(v)}'}$
with continuous action of
${\pmb {\mathscr {S}}}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{(v)}'}$
with continuous action of
![]() $\mathbf {G}(\mathbb {A}_f^p)$
, with
$\mathbf {G}(\mathbb {A}_f^p)$
, with
![]() $\mathcal{O}_{(v)}'=\mathcal{O}_{\mathbf {E}'}\otimes _{\mathcal{O}_{\mathbf {E}}}\mathcal{O}_{(v)}$
.Footnote
8
$\mathcal{O}_{(v)}'=\mathcal{O}_{\mathbf {E}'}\otimes _{\mathcal{O}_{\mathbf {E}}}\mathcal{O}_{(v)}$
.Footnote
8
Step 4: The construction in the local setting
Consider
That
![]() $\mathbf {E}'$
is completely split over
$\mathbf {E}'$
is completely split over
![]() $\mathbf {E}$
at every prime over p implies, in particular, that this decomposes as several copies of the same
$\mathbf {E}$
at every prime over p implies, in particular, that this decomposes as several copies of the same
![]() $\mathcal{O}_v$
-scheme with a continuous action of
$\mathcal{O}_v$
-scheme with a continuous action of
![]() $\mathbf {G}(\mathbb {A}_f^p)$
, indexed by by the place of
$\mathbf {G}(\mathbb {A}_f^p)$
, indexed by by the place of
![]() $\mathbf {E}'$
lying over v. Choose any of these copies, and call it
$\mathbf {E}'$
lying over v. Choose any of these copies, and call it
![]() $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
. Observe that we have a decomposition
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
. Observe that we have a decomposition
where ![]() is any copy of
is any copy of ![]() pulled back to
pulled back to
![]() $\mathcal{O}_E^{\textrm {ur}}$
. We then set
$\mathcal{O}_E^{\textrm {ur}}$
. We then set
for any neat compact open subgroup
![]() $\mathsf {K}^p$
of
$\mathsf {K}^p$
of
![]() $\mathbf {G}(\mathbb {A}_f^p)$
. That these quotients exist and are quasi-projective can be deduced from Remark 3.14 in conjunction with [SP17, Tag 01ZY] and [SP17, Tag 07S6].
$\mathbf {G}(\mathbb {A}_f^p)$
. That these quotients exist and are quasi-projective can be deduced from Remark 3.14 in conjunction with [SP17, Tag 01ZY] and [SP17, Tag 07S6].
Remark 3.19. Let us briefly explain how to view (3.13) as an integral model for
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
. By [Reference Kisin and PappasKP18, Proposition 4.6.13], there is a canonical decomposition
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
. By [Reference Kisin and PappasKP18, Proposition 4.6.13], there is a canonical decomposition
 $$ \begin{align} \textrm{Sh}_{\mathsf{K}_p}(\mathbf{G},\mathbf{X})_{E^{\textrm{ur}}}= \bigsqcup_{j \in J}\left([\textrm{Sh}_{\mathsf{K}_{p,1}}(\mathbf{G}_1,\mathbf{X}_1)_{E^{\textrm{ur}}}^+\times \mathscr{A}(\boldsymbol{\mathcal{G}})j]/\mathscr{A}(\boldsymbol{\mathcal{G}}_1)^\circ\right), \end{align} $$
$$ \begin{align} \textrm{Sh}_{\mathsf{K}_p}(\mathbf{G},\mathbf{X})_{E^{\textrm{ur}}}= \bigsqcup_{j \in J}\left([\textrm{Sh}_{\mathsf{K}_{p,1}}(\mathbf{G}_1,\mathbf{X}_1)_{E^{\textrm{ur}}}^+\times \mathscr{A}(\boldsymbol{\mathcal{G}})j]/\mathscr{A}(\boldsymbol{\mathcal{G}}_1)^\circ\right), \end{align} $$
where (among other definitions) this
![]() $\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)_{E^{\textrm {ur}}}^+$
is the generic fiber of
$\textrm {Sh}_{\mathsf {K}_{p,1}}(\mathbf {G}_1,\mathbf {X}_1)_{E^{\textrm {ur}}}^+$
is the generic fiber of ![]() . For clarity, denote the jth component of the right-hand side of (3.14) by
. For clarity, denote the jth component of the right-hand side of (3.14) by
![]() $\mathscr {X}_j$
. The isomorphism between the generic fiber of the right-hand side of (3.13) and the right-hand side of (3.14) is determined by
$\mathscr {X}_j$
. The isomorphism between the generic fiber of the right-hand side of (3.13) and the right-hand side of (3.14) is determined by
where the first map is the tautological one, and the second is given by multiplication by j viewed as an element of
![]() $\mathscr {A}(\mathbf {G})$
.
$\mathscr {A}(\mathbf {G})$
.
3.4 Some properties and functoriality results
In this subsection we establish some compatibilities satisfied by the Kisin–Pappas–Zhou integral models, and we prove the minimal amount of functoriality needed to prove our main result (see Theorem 4.10). This main result will then establish functoriality in general (see Theorem 4.14).
Kisin–Pappas–Zhou integral models of toral type
To utilize the results of [Reference DanielsDan25], it is useful to explicitly describe Kisin–Pappas–Zhou integral models of tori.
Recall from Example 3.7 that a Shimura datum
![]() $(\mathbf {T},\{h\})$
is of toral type if
$(\mathbf {T},\{h\})$
is of toral type if
![]() $\mathbf {T}$
is a torus. In this case, for every compact open subgroup
$\mathbf {T}$
is a torus. In this case, for every compact open subgroup
![]() $\mathsf {K} = \mathsf {K}_p\mathsf { K}^p \subseteq \mathbf {T}(\mathbb {A}_f^p)$
, the Shimura variety
$\mathsf {K} = \mathsf {K}_p\mathsf { K}^p \subseteq \mathbf {T}(\mathbb {A}_f^p)$
, the Shimura variety
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {T},\{h\})$
is zero-dimensional, i.e.,
$\textrm {Sh}_{\mathsf {K}}(\mathbf {T},\{h\})$
is zero-dimensional, i.e.,
for some finite index set I. In fact, each field
![]() $E_i$
is the same field, and is an unramified extension of
$E_i$
is the same field, and is an unramified extension of
![]() $\mathbb {Q}_p$
(see [Reference DanielsDan25, Lemma 4.2] and the proof of [Reference DanielsDan25, Lemma 4.8]).
$\mathbb {Q}_p$
(see [Reference DanielsDan25, Lemma 4.2] and the proof of [Reference DanielsDan25, Lemma 4.8]).
Set
![]() $T=\mathbf {T}_{\mathbb {Q}_p}$
. As discussed in §2.1, there is a unique parahoric model
$T=\mathbf {T}_{\mathbb {Q}_p}$
. As discussed in §2.1, there is a unique parahoric model
![]() $\mathcal{T}$
of T, given by the connected component
$\mathcal{T}$
of T, given by the connected component
![]() $(\mathcal{T}^{\textrm {lft}})^\circ $
of the Néron model
$(\mathcal{T}^{\textrm {lft}})^\circ $
of the Néron model
![]() $\mathcal{T}^{\textrm {lft}}$
of T.
$\mathcal{T}^{\textrm {lft}}$
of T.
Proposition 3.20. Suppose
![]() $(\mathbf {T},\{h\}, \mathcal{T})$
is parahoric Shimura datum of toral type, and let
$(\mathbf {T},\{h\}, \mathcal{T})$
is parahoric Shimura datum of toral type, and let
![]() $\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
be a parahoric Shimura datum of Hodge type which is well-adapted to
$\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
be a parahoric Shimura datum of Hodge type which is well-adapted to
![]() $(\mathbf {T}, \{h\}, \mathcal{T})$
and for which
$(\mathbf {T}, \{h\}, \mathcal{T})$
and for which
![]() $Z(G_1)$
is R-smooth. Then,
$Z(G_1)$
is R-smooth. Then,
for any neat compact open subgroup
![]() $\mathsf {K}^p\subseteq \mathbf {T}(\mathbb {A}_f^p)$
and with
$\mathsf {K}^p\subseteq \mathbf {T}(\mathbb {A}_f^p)$
and with
![]() $\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
. The same holds true for
$\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
. The same holds true for ![]() if
if
![]() $(\mathbf {T}, \{h\})$
is of Hodge type.
$(\mathbf {T}, \{h\})$
is of Hodge type.
Proof. First, observe that as
![]() $(\mathbf {G}_1, \mathbf {X}_1)$
is adapted to the datum
$(\mathbf {G}_1, \mathbf {X}_1)$
is adapted to the datum
![]() $(\mathbf {T}, \{h\})$
, we have an isogeny
$(\mathbf {T}, \{h\})$
, we have an isogeny
![]() $\mathbf {G}_1^{\mathrm {der}} \to \mathbf {T}^{\mathrm {der}} = \{e\}$
, and hence
$\mathbf {G}_1^{\mathrm {der}} \to \mathbf {T}^{\mathrm {der}} = \{e\}$
, and hence
![]() $\mathbf {G}_1^{\mathrm {der}}$
is trivial, since it is connected. Thus,
$\mathbf {G}_1^{\mathrm {der}}$
is trivial, since it is connected. Thus,
![]() $\mathbf {G}_1$
is a torus.Footnote
9
Consider an arbitrary neat compact open subgroup
$\mathbf {G}_1$
is a torus.Footnote
9
Consider an arbitrary neat compact open subgroup
![]() $\mathsf {K}^p_1\subseteq \mathbf {G}_1(\mathbb {A}_f^p)$
.
$\mathsf {K}^p_1\subseteq \mathbf {G}_1(\mathbb {A}_f^p)$
.
Choose a parahoric Hodge embedding
![]() $\iota \colon (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1) \to (\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm ,\textrm {GSp}(\Lambda ))$
which respects stabilizers, and a neat compact open subgroup
$\iota \colon (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1) \to (\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm ,\textrm {GSp}(\Lambda ))$
which respects stabilizers, and a neat compact open subgroup
![]() $\mathsf {L}_1^p \subseteq \textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}} \mathbb {A}_f^p)$
such that
$\mathsf {L}_1^p \subseteq \textrm {GSp}(\mathbf {V}\otimes _{\mathbb {Q}} \mathbb {A}_f^p)$
such that
![]() $\iota (\mathsf { K}_{1,p}\mathsf {K}^p_1) \subseteq \textrm {GSp}(\Lambda )\mathsf {L}_1^p$
, inducing a closed embedding
$\iota (\mathsf { K}_{1,p}\mathsf {K}^p_1) \subseteq \textrm {GSp}(\Lambda )\mathsf {L}_1^p$
, inducing a closed embedding
Note that
![]() ${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf { L}_1^p}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
is flat, separated, and finite over
${\pmb {\mathscr {S}}}_{\textrm {GSp}(\Lambda )\mathsf { L}_1^p}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
is flat, separated, and finite over
![]() $\mathbb {Z}_{(p)}$
. Thus, considering (3.15), and using notation from Step 2 of §3.3, it follows from Lemma 3.21 below that
$\mathbb {Z}_{(p)}$
. Thus, considering (3.15), and using notation from Step 2 of §3.3, it follows from Lemma 3.21 below that ![]() and thus
and thus ![]() are disjoint unions of semi-local localizations of
are disjoint unions of semi-local localizations of
![]() $\mathcal{O}_{\mathbf {F}}$
for some finite extension
$\mathcal{O}_{\mathbf {F}}$
for some finite extension
![]() $\mathbf {F}$
of
$\mathbf {F}$
of
![]() $\mathbf {E}$
.
$\mathbf {E}$
.
This implies that, using notation now from Step 3 of §3.3, that ![]() is either the spectrum of a field or of a semi-local Dedekind domain. Thus, from the construction in Step 4 of §3.3 we deduce that for each neat compact open
is either the spectrum of a field or of a semi-local Dedekind domain. Thus, from the construction in Step 4 of §3.3 we deduce that for each neat compact open
![]() $\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
one has that
$\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
one has that
![]() $\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
is either the disjoint union of spectra of extensions of E, or the disjoint union of spectra of the rings of integers of finite extensions of E. That said, the former is impossible as it is then clear that such a model cannot satisfy the extension property from (2) of Theorem 3.9, and so the latter must hold. The fist claim follows. Moreover, the second claim follows from similar arguments.
$\mathscr {S}_{\mathsf {K}_p\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
is either the disjoint union of spectra of extensions of E, or the disjoint union of spectra of the rings of integers of finite extensions of E. That said, the former is impossible as it is then clear that such a model cannot satisfy the extension property from (2) of Theorem 3.9, and so the latter must hold. The fist claim follows. Moreover, the second claim follows from similar arguments.
Following [SP17, Tag 035E], if X is a scheme with the property that every quasi-compact open has finitely many connected components, then we denote the normalization of X by
![]() $X^\nu $
.
$X^\nu $
.
Lemma 3.21. Let
![]() $\mathcal{O}$
be an excellent Dedekind domain and
$\mathcal{O}$
be an excellent Dedekind domain and
![]() $\mathscr {X}$
be a separated, finite type, flat
$\mathscr {X}$
be a separated, finite type, flat
![]() $\mathcal{O}$
-scheme. Let x is a closed point of
$\mathcal{O}$
-scheme. Let x is a closed point of
![]() $\mathscr {X}_\eta $
and let
$\mathscr {X}_\eta $
and let
![]() $\overline {x}$
be the Zariski closure of x in
$\overline {x}$
be the Zariski closure of x in
![]() $\mathscr {X}$
. Then,
$\mathscr {X}$
. Then,
![]() $\overline {x}^\nu $
is an open subscheme of
$\overline {x}^\nu $
is an open subscheme of
![]() $\mathrm{Spec}\,(\mathcal{O}')$
for a Dedekind domain
$\mathrm{Spec}\,(\mathcal{O}')$
for a Dedekind domain
![]() $\mathcal{O}'$
finite flat over
$\mathcal{O}'$
finite flat over
![]() $\mathcal{O}$
.
$\mathcal{O}$
.
Proof. Let
![]() $\overline {X}$
be a compactification of
$\overline {X}$
be a compactification of
![]() $\mathscr {X}\to \mathrm{Spec}\,(\mathcal{O})$
(see [SP17, Tag 0ATT] and [SP17, Tag 0F41]). Replacing
$\mathscr {X}\to \mathrm{Spec}\,(\mathcal{O})$
(see [SP17, Tag 0ATT] and [SP17, Tag 0F41]). Replacing
![]() $\overline {\mathscr {X}}$
with the closed subscheme cut out by the
$\overline {\mathscr {X}}$
with the closed subscheme cut out by the
![]() $\mathcal{O}$
-torsion in
$\mathcal{O}$
-torsion in
![]() $\mathcal{O}_{\mathscr {X}}$
, we may assume that
$\mathcal{O}_{\mathscr {X}}$
, we may assume that
![]() $\overline {\mathscr {X}}$
is flat over
$\overline {\mathscr {X}}$
is flat over
![]() $\mathcal{O}$
(see [Reference Görtz and WedhornGW20, Proposition 14.14]).
$\mathcal{O}$
(see [Reference Görtz and WedhornGW20, Proposition 14.14]).
Let Z denote the Zariski closure of x in
![]() $\overline {\mathscr {X}}$
. We claim that
$\overline {\mathscr {X}}$
. We claim that
![]() $Z^\nu =\mathrm{Spec}\,(\mathcal{O}')$
for a Dedekind ring
$Z^\nu =\mathrm{Spec}\,(\mathcal{O}')$
for a Dedekind ring
![]() $\mathcal{O}'$
finite flat over
$\mathcal{O}'$
finite flat over
![]() $\mathcal{O}$
. As
$\mathcal{O}$
. As
![]() $\overline {x}=\mathscr {X}\cap Z$
, the lemma will then follow from [SP17, Tag 035K]. To prove the claim, we observe that Z is evidently irreducible and reduced, and thus integral. But, as
$\overline {x}=\mathscr {X}\cap Z$
, the lemma will then follow from [SP17, Tag 035K]. To prove the claim, we observe that Z is evidently irreducible and reduced, and thus integral. But, as
![]() $Z\to \textrm {Spec}(\mathcal{O})$
is dominant, we deduce that it is flat by [Reference Görtz and WedhornGW20, Proposition 14.14]. But, since
$Z\to \textrm {Spec}(\mathcal{O})$
is dominant, we deduce that it is flat by [Reference Görtz and WedhornGW20, Proposition 14.14]. But, since
![]() $\overline {\mathscr {X}}$
is a proper
$\overline {\mathscr {X}}$
is a proper
![]() $\mathcal{O}$
-scheme, so is Z. Thus, by [SP17, Tag 0D4J] we deduce that
$\mathcal{O}$
-scheme, so is Z. Thus, by [SP17, Tag 0D4J] we deduce that
![]() $Z_s$
is zero dimensional. Thus,
$Z_s$
is zero dimensional. Thus,
![]() $Z\to \mathrm{Spec}\,(\mathcal{O})$
is proper and quasi-finite, and so finite (see [SP17, Tag 02OG]). It follows that
$Z\to \mathrm{Spec}\,(\mathcal{O})$
is proper and quasi-finite, and so finite (see [SP17, Tag 02OG]). It follows that
![]() $Z^\nu $
is also an integral scheme and
$Z^\nu $
is also an integral scheme and
![]() $ Z^\nu \to \mathrm{Spec}\,(\mathcal{O})$
is dominant and finite (using [SP17, Tag 035R]) over
$ Z^\nu \to \mathrm{Spec}\,(\mathcal{O})$
is dominant and finite (using [SP17, Tag 035R]) over
![]() $\mathcal{O}$
and so flat again by [Reference Görtz and WedhornGW20, Proposition 14.14]. Write
$\mathcal{O}$
and so flat again by [Reference Görtz and WedhornGW20, Proposition 14.14]. Write
![]() $Z^\nu =\mathrm{Spec}\,(\mathcal{O}')$
, then
$Z^\nu =\mathrm{Spec}\,(\mathcal{O}')$
, then
![]() $\mathcal{O}'$
is
$\mathcal{O}'$
is
![]() $1$
-dimensional Noetherian normal domain, and so a Dedekind domain as desired.
$1$
-dimensional Noetherian normal domain, and so a Dedekind domain as desired.
Given Proposition 3.20, we see that the definition of
![]() $\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}} (\mathbf {T},\{h\})$
is independent of the choice of
$\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}} (\mathbf {T},\{h\})$
is independent of the choice of
![]() $\mathfrak {d}$
. We denote by
$\mathfrak {d}$
. We denote by
![]() $\mathscr {S}_{\mathsf {K}}(\mathbf {T},\{h\})$
the common object.
$\mathscr {S}_{\mathsf {K}}(\mathbf {T},\{h\})$
the common object.
Functoriality for ad-isomorphisms
Suppose that
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
is an ad-isomorphism of parahoric abelian-type Shimura data. Take a parahoric Shimura datum
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
is an ad-isomorphism of parahoric abelian-type Shimura data. Take a parahoric Shimura datum
![]() $\mathfrak {d}=(\mathbf {G}_2,\mathbf {X}_2,\mathcal{G}_2)$
of Hodge type well-adapted to
$\mathfrak {d}=(\mathbf {G}_2,\mathbf {X}_2,\mathcal{G}_2)$
of Hodge type well-adapted to
![]() $(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
for which
$(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
for which
![]() $Z(G_2)$
is R-smooth. Since
$Z(G_2)$
is R-smooth. Since
![]() $\alpha $
is an ad-isomorphism, one sees that
$\alpha $
is an ad-isomorphism, one sees that
![]() $\mathfrak {d}$
is also well-adapted to
$\mathfrak {d}$
is also well-adapted to
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
in the obvious way.
$(\mathbf {G},\mathbf {X},\mathcal{G})$
in the obvious way.
Proposition 3.22. There exists a unique quotient-finite étale morphism
which is equivariant for the map
![]() $\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
and models
$\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
and models
Here by quotient-finite étale we mean that if
![]() $\mathsf {K}_1^p\subseteq \mathbf {G}_1(\mathbb {A}_f^p)$
and
$\mathsf {K}_1^p\subseteq \mathbf {G}_1(\mathbb {A}_f^p)$
and
![]() $\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
are neat compact open subgroups such that
$\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
are neat compact open subgroups such that
![]() $\alpha (\mathsf {K}_1^p)\subseteq \mathsf {K}^p$
, then the induced map
$\alpha (\mathsf {K}_1^p)\subseteq \mathsf {K}^p$
, then the induced map
is a finite étale morphism.
Proof of Proposition 3.22.
The fact that such a map is unique is clear by the separatedness of
![]() $\alpha $
and the flatness of
$\alpha $
and the flatness of
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}^p_1}(\mathbf {G}_1,\mathbf {X}_1)$
, which guarantees that its generic fiber is Zariski dense (e.g., see [Reference Görtz and WedhornGW20, Proposition 14.14]).
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}^p_1}(\mathbf {G}_1,\mathbf {X}_1)$
, which guarantees that its generic fiber is Zariski dense (e.g., see [Reference Görtz and WedhornGW20, Proposition 14.14]).
To see the existence, we note that by definition we have
and
Now, by Lemma 3.12 and Lemma 3.13 we get morphisms
Because
![]() $\alpha (\mathsf {K}_{p,1})\subseteq \mathsf {K}_p$
, we have a map of sets
$\alpha (\mathsf {K}_{p,1})\subseteq \mathsf {K}_p$
, we have a map of sets
![]() $\alpha \colon J_1\to J$
. Since the isomorphism from (3.5) is natural in these operations, we deduce the existence of a map
$\alpha \colon J_1\to J$
. Since the isomorphism from (3.5) is natural in these operations, we deduce the existence of a map
equivariant for
![]() $\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
. That the generic fiber of this map agrees with
$\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
. That the generic fiber of this map agrees with
follows as in [Reference Kisin and PappasKP18, Lemma 4.6.13].
Finally, we show that
![]() $\alpha $
is quotient-finite étale. Let
$\alpha $
is quotient-finite étale. Let
![]() $\mathscr {S}_1^+$
denote a connected component of
$\mathscr {S}_1^+$
denote a connected component of
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_{p,1}}(\mathbf {G}_1, \mathbf {X}_1)$
mapping to a connected component
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_{p,1}}(\mathbf {G}_1, \mathbf {X}_1)$
mapping to a connected component
![]() $\mathscr {S}^+$
of
$\mathscr {S}^+$
of
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p}(\mathbf {G}, \mathbf {X})_{\mathcal{O}_{E_1}}$
. By construction, we have
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}_p}(\mathbf {G}, \mathbf {X})_{\mathcal{O}_{E_1}}$
. By construction, we have
where
(see also the arguments of [Reference Kisin and PappasKP18, Corollary 4.6.15]). Thus
![]() $\mathscr {S}^+$
is the quotient of
$\mathscr {S}^+$
is the quotient of
![]() $\mathscr {S}_1^+$
by the finite group
$\mathscr {S}_1^+$
by the finite group
![]() $\Delta / \Delta _1$
, and the result follows.
$\Delta / \Delta _1$
, and the result follows.
In particular, the proposition implies functoriality for morphisms
![]() $(\mathbf {T}_1, \{h_1\}, \mathcal{T}_1) \to (\mathbf {T}, \{h\}, \mathcal{T})$
of parahoric Shimura data of toral type.
$(\mathbf {T}_1, \{h_1\}, \mathcal{T}_1) \to (\mathbf {T}, \{h\}, \mathcal{T})$
of parahoric Shimura data of toral type.
Functoriality for abelianizations
Suppose now that
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Consider the parahoric Shimura datum
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Consider the parahoric Shimura datum
![]() $(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}}, \mathcal{G}^{\text {ab}})$
, where
$(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}}, \mathcal{G}^{\text {ab}})$
, where
![]() $\mathbf {X}^{\text {ab}}$
is the result of post-composing any element h of
$\mathbf {X}^{\text {ab}}$
is the result of post-composing any element h of
![]() $\mathbf {X}$
with the canonical map
$\mathbf {X}$
with the canonical map
![]() $\delta : \mathbf {G} \to \mathbf {G}^{\text {ab}}$
. We have the obvious associated morphism of parahoric Shimura data
$\delta : \mathbf {G} \to \mathbf {G}^{\text {ab}}$
. We have the obvious associated morphism of parahoric Shimura data
Write
![]() $\mathsf {K}_p^{\text {ab}} = \mathcal{G}^{\text {ab}}(\mathbb {Z}_p)$
.
$\mathsf {K}_p^{\text {ab}} = \mathcal{G}^{\text {ab}}(\mathbb {Z}_p)$
.
Proposition 3.23. There exists a unique
which is equivariant for the map
![]() $\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
and models
$\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
and models
Proof. Given the descriptions of
![]() $\textrm {Sh}_{\mathsf {K}_p^{\text {ab}}}(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})$
and
$\textrm {Sh}_{\mathsf {K}_p^{\text {ab}}}(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})$
and
![]() $\mathscr {S}_{\mathsf {K}_p^{\text {ab}}}(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})_{\mathcal{O}_E}$
from (3.15) and Proposition 3.20, respectively, the result follows from Lemma 3.24. More precisely, it suffices to construct maps at every finite level. But, by Proposition 3.20, the Kisin–Pappas–Zhou model
$\mathscr {S}_{\mathsf {K}_p^{\text {ab}}}(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})_{\mathcal{O}_E}$
from (3.15) and Proposition 3.20, respectively, the result follows from Lemma 3.24. More precisely, it suffices to construct maps at every finite level. But, by Proposition 3.20, the Kisin–Pappas–Zhou model
![]() $S'$
for
$S'$
for
![]() $(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})$
base-changed to
$(\mathbf {G}^{\text {ab}}, \mathbf {X}^{\text {ab}})$
base-changed to
![]() $\mathcal{O}_E$
is finite flat over
$\mathcal{O}_E$
is finite flat over
![]() $S = \mathrm{Spec}\,(\mathcal{O}_E)$
. On the other hand, the finite levels X of the Kisin–Pappas–Zhou models X for
$S = \mathrm{Spec}\,(\mathcal{O}_E)$
. On the other hand, the finite levels X of the Kisin–Pappas–Zhou models X for
![]() $(\mathbf {G}, \mathbf {X})$
are normal and quasi-projective and flat over S. Thus may apply Lemma 3.24 to the map at finite levels on the generic fiber.
$(\mathbf {G}, \mathbf {X})$
are normal and quasi-projective and flat over S. Thus may apply Lemma 3.24 to the map at finite levels on the generic fiber.
Lemma 3.24. Suppose that S is a scheme and U is an open subscheme of S which is schematically dense and for which the inclusion
![]() $U \hookrightarrow S$
is quasi-compact. Given a diagram
$U \hookrightarrow S$
is quasi-compact. Given a diagram

with X a normal scheme,
![]() $S'$
a scheme, f quasi-compact, separated, and flat, and g quasi-compact, flat, and integral, there exists a unique arrow dashed arrow as in the diagram above which makes the top square Cartesian.
$S'$
a scheme, f quasi-compact, separated, and flat, and g quasi-compact, flat, and integral, there exists a unique arrow dashed arrow as in the diagram above which makes the top square Cartesian.
Proof. By [SP17, Tag 081H],
![]() $X_U \subseteq X$
is schematically dense, so the uniqueness follows from [SP17, Tag 01RH]. In turn, by uniqueness, we may localize on S and X to prove existence. Using that g is affine, we may then assume without loss of generality that
$X_U \subseteq X$
is schematically dense, so the uniqueness follows from [SP17, Tag 01RH]. In turn, by uniqueness, we may localize on S and X to prove existence. Using that g is affine, we may then assume without loss of generality that
![]() $S = \mathrm{Spec}\,(A)$
,
$S = \mathrm{Spec}\,(A)$
,
![]() $S' = \mathrm{Spec}\,(A')$
and
$S' = \mathrm{Spec}\,(A')$
and
![]() $A \to A'$
is integral. Moreover, localizing on X we may further assume
$A \to A'$
is integral. Moreover, localizing on X we may further assume
![]() $X = \mathrm{Spec}\,(B)$
with B a normal domain. We then have the following diagram of rings
$X = \mathrm{Spec}\,(B)$
with B a normal domain. We then have the following diagram of rings

The center and right-hand vertical arrows are injections by flatness of f and g along with [SP17, Tag 081H] and [SP17, Tag 01RE].
We claim that
![]() $\alpha (A') \subseteq B$
. Indeed, let
$\alpha (A') \subseteq B$
. Indeed, let
![]() $a' \in A'$
. Then by integrality of
$a' \in A'$
. Then by integrality of
![]() $A \to A'$
, there exists a monic polynomial
$A \to A'$
, there exists a monic polynomial
![]() $p(T)$
in
$p(T)$
in
![]() $A[T]$
such that
$A[T]$
such that
![]() $p(a') = 0$
. But then
$p(a') = 0$
. But then
![]() $\alpha (a')$
in
$\alpha (a')$
in
![]() $\mathcal{O}(X_U)$
satisfies the monic polynomial
$\mathcal{O}(X_U)$
satisfies the monic polynomial
![]() $f(p)(T)$
in
$f(p)(T)$
in
![]() $B[T]$
. Thus
$B[T]$
. Thus
![]() $\alpha (a')$
must lie in B by normality of B.
$\alpha (a')$
must lie in B by normality of B.
It follows that we have a map
![]() $\mathrm{Spec}\,(\alpha ): \mathrm{Spec}\,(B) \to \mathrm{Spec}\, (A')$
. We claim that the diagram
$\mathrm{Spec}\,(\alpha ): \mathrm{Spec}\,(B) \to \mathrm{Spec}\, (A')$
. We claim that the diagram

is Cartesian. For this it is enough to show that
![]() $\mathrm{Spec}\,(\alpha ) \big |_{X_U} = \alpha $
. Since
$\mathrm{Spec}\,(\alpha ) \big |_{X_U} = \alpha $
. Since
![]() $U \hookrightarrow X$
is quasi-compact, U is quasi-compact, and therefore the same is true of
$U \hookrightarrow X$
is quasi-compact, U is quasi-compact, and therefore the same is true of
![]() $S_U'$
and
$S_U'$
and
![]() $X_U$
by quasi-compactness of f and g. Since
$X_U$
by quasi-compactness of f and g. Since
![]() $\mathrm{Spec}\,(\alpha )$
and
$\mathrm{Spec}\,(\alpha )$
and
![]() $\alpha $
induce the same map
$\alpha $
induce the same map
![]() $\mathcal{O}(S^{\prime }_U) \to \mathcal{O}(X_U)$
, the result now follows from [SP17, Tag 01P9].
$\mathcal{O}(S^{\prime }_U) \to \mathcal{O}(X_U)$
, the result now follows from [SP17, Tag 01P9].
Two constructions for Hodge-type data
We record here the following basic compatibility between the constructions made in §3.3. Let
![]() $\mathfrak {d}=(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura datum of Hodge type and assume
$\mathfrak {d}=(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura datum of Hodge type and assume
![]() $Z(G)$
is an R-smooth torus.
$Z(G)$
is an R-smooth torus.
Proposition 3.25. There is a canonical
![]() $\mathbf {G}(\mathbb {A}^p_f)$
-equivariant identification
$\mathbf {G}(\mathbb {A}^p_f)$
-equivariant identification
extending the identity in the generic fiber.
Proof. Choose a
![]() $\mathsf {K}^p \subset G(\mathbb {A}_f^p)$
and let
$\mathsf {K}^p \subset G(\mathbb {A}_f^p)$
and let
![]() $\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
. Implementing Zarhin’s trick, we may choose a parahoric Hodge embedding
$\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
. Implementing Zarhin’s trick, we may choose a parahoric Hodge embedding
![]() $\iota \colon (\mathbf {G}, \mathbf {X}, \mathcal{G}) \to (\textrm {GSp}(\mathbf {V}), \mathfrak {h}^\pm , \textrm {GSp}(\Lambda ))$
such that
$\iota \colon (\mathbf {G}, \mathbf {X}, \mathcal{G}) \to (\textrm {GSp}(\mathbf {V}), \mathfrak {h}^\pm , \textrm {GSp}(\Lambda ))$
such that
![]() $\textrm {GSp}(\Lambda )$
is reductive. Moreover, as in §3.3, we may choose a level
$\textrm {GSp}(\Lambda )$
is reductive. Moreover, as in §3.3, we may choose a level
![]() $\mathsf {L}_p\mathsf {L}^p \subset $
such that
$\mathsf {L}_p\mathsf {L}^p \subset $
such that
![]() $\iota $
maps
$\iota $
maps
![]() $\mathsf {K}$
into
$\mathsf {K}$
into
![]() $\mathsf {L}$
, such that there is a morphism
$\mathsf {L}$
, such that there is a morphism
which is the normalization of a closed embedding.
Next observe that the statement of the proposition holds for
![]() $(\textrm {GSp}(\mathbf {V}), \mathfrak {h}^\pm , \textrm {GSp}(\Lambda ))$
by [Reference KisinKis10, Theorem 3.4.10] (which establishes that the source and target are both integral canonical models in the sense of op. cit.). Moreover, for any connected component
$(\textrm {GSp}(\mathbf {V}), \mathfrak {h}^\pm , \textrm {GSp}(\Lambda ))$
by [Reference KisinKis10, Theorem 3.4.10] (which establishes that the source and target are both integral canonical models in the sense of op. cit.). Moreover, for any connected component ![]() , there is a tautological map from
, there is a tautological map from ![]() to some connected component
to some connected component
![]() $\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )^+$
of
$\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )^+$
of
![]() $\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
. Applying the functorialities of the
$\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
. Applying the functorialities of the
![]() $\mathscr {A}$
-groups as established in §3.2, and the Siegel case of the proposition, we obtain a map
$\mathscr {A}$
-groups as established in §3.2, and the Siegel case of the proposition, we obtain a map
As
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
is dense in the integral model
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
is dense in the integral model
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, the map (3.18) carries
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, the map (3.18) carries
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
into the closure of
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
into the closure of
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
inside of
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
inside of
![]() $\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
. Moreover, since
$\mathscr {S}_{\mathsf {L}}(\mathbf {GSp}(\mathbf {V}),\mathfrak {h}^\pm )$
. Moreover, since
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
is normal, the map (3.18) factors through (3.17). Since
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
is normal, the map (3.18) factors through (3.17). Since
![]() $\mathcal{G} \to \textrm {GSp}(\Lambda )$
is a closed embedding, one deduces that (3.17) is quasi-finite, and thus so is the map
$\mathcal{G} \to \textrm {GSp}(\Lambda )$
is a closed embedding, one deduces that (3.17) is quasi-finite, and thus so is the map ![]() . As both source and target are normal, and this map induces an isomorphism on the dense open
. As both source and target are normal, and this map induces an isomorphism on the dense open
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, we deduce it is an isomorphism by Zariski’s Main Theorem.
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})$
, we deduce it is an isomorphism by Zariski’s Main Theorem.
This procedure is clearly compatible with varying
![]() $\mathsf {K}^p$
, so we obtain the desired result by passing to the limit.
$\mathsf {K}^p$
, so we obtain the desired result by passing to the limit.
Kisin–Pappas–Zhou integral models for some products
Let
![]() $\mathfrak {d} = (\mathbf {G}, \mathbf {X}, \mathcal{G})$
be a parahoric Shimura datum of Hodge type such that
$\mathfrak {d} = (\mathbf {G}, \mathbf {X}, \mathcal{G})$
be a parahoric Shimura datum of Hodge type such that
![]() $Z(G)$
is an R-smooth torus, and that
$Z(G)$
is an R-smooth torus, and that
![]() $(\mathbf {T}, \{h\}, \mathcal{T})$
is a parahoric Shimura datum of toral type. Write
$(\mathbf {T}, \{h\}, \mathcal{T})$
is a parahoric Shimura datum of toral type. Write
![]() $\mathbf {E}'$
for the compositum of the reflex fields of the two Shimura data, which is the reflex field of
$\mathbf {E}'$
for the compositum of the reflex fields of the two Shimura data, which is the reflex field of
![]() $(\mathbf {G}\times \mathbf {T}, \mathbf {X}\times \{h\})$
, and set
$(\mathbf {G}\times \mathbf {T}, \mathbf {X}\times \{h\})$
, and set
![]() $\mathsf {M}_p = \mathcal{T}(\mathbb {Z}_p)$
.
$\mathsf {M}_p = \mathcal{T}(\mathbb {Z}_p)$
.
Proposition 3.26. There is a canonical
![]() $\mathbf {G}(\mathbb {A}^p_f)\times \mathbf {T}(\mathbb {A}_f^p)$
-equivariant identification
$\mathbf {G}(\mathbb {A}^p_f)\times \mathbf {T}(\mathbb {A}_f^p)$
-equivariant identification
Proof. The projection map
![]() $\mathbf {G}\times \mathbf {T} \to \mathbf {G}$
is an ad-isomorphism, so by Proposition 3.22, we have a quotient-finite map
$\mathbf {G}\times \mathbf {T} \to \mathbf {G}$
is an ad-isomorphism, so by Proposition 3.22, we have a quotient-finite map
extending the morphism on the generic fibers which is equivariant for the projection
![]() $(\mathbf {G}\times \mathbf {T})(\mathbb {A}_f^p) \to \mathbf {G}(\mathbb {A}_f^p)$
. On the other hand, the map of reductive groups
$(\mathbf {G}\times \mathbf {T})(\mathbb {A}_f^p) \to \mathbf {G}(\mathbb {A}_f^p)$
. On the other hand, the map of reductive groups
![]() $\mathbf {G} \times \mathbf {T} \to \mathbf {T}$
factors through
$\mathbf {G} \times \mathbf {T} \to \mathbf {T}$
factors through
![]() $(\mathbf {G} \times \mathbf {T})^{\text {ab}}$
, which is a torus. Hence Proposition 3.22 and Proposition 3.23 combine to furnish us with a map
$(\mathbf {G} \times \mathbf {T})^{\text {ab}}$
, which is a torus. Hence Proposition 3.22 and Proposition 3.23 combine to furnish us with a map
extending the morphism on generic fibers, which is equivariant for
![]() $(\mathbf {G} \times \mathbf {T})(\mathbb {A}_f^p) \to \mathbf {T}(\mathbb {A}_f^p)$
. From these, we obtain the map
$(\mathbf {G} \times \mathbf {T})(\mathbb {A}_f^p) \to \mathbf {T}(\mathbb {A}_f^p)$
. From these, we obtain the map
which is equivariant for ![]() . The map (3.20) is an isomorphism on generic fibers, and is quasi-finite at each finite level because (3.19) is quotient-finite. It follows that (3.20) is an isomorphism by the argument at the end of the proof of Proposition 3.25.
. The map (3.20) is an isomorphism on generic fibers, and is quasi-finite at each finite level because (3.19) is quotient-finite. It follows that (3.20) is an isomorphism by the argument at the end of the proof of Proposition 3.25.
4 The Pappas–Rapoport conjecture
In this section we state the Pappas–Rapoport conjecture and recall the cases in which it has been previously proven. We also state our main theorem and applications.
As in §3.3, throughout this section we often use the following notation and data:

4.1 The Pappas–Rapoport conjecture
We now recall the formulation of the Pappas–Rapoport conjecture as given in [Reference Pappas and RapoportPR24] and extended in [Reference DanielsDan25].
The group
 $\mathcal{G}^c$
$\mathcal{G}^c$
In contrast to the case of Shimura varieties of Hodge type discussed in [Reference Pappas and RapoportPR24], to obtain shtukas on arbitrary Shimura varieties of abelian type, one must consider a modification
![]() $\mathcal{G}^c$
of the parahoric group
$\mathcal{G}^c$
of the parahoric group
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
Let
![]() $\mathbf {T}$
be a multiplicative group over
$\mathbf {T}$
be a multiplicative group over
![]() $\mathbb {Q}$
. We denote by
$\mathbb {Q}$
. We denote by
![]() $\mathbf {T}_{\textrm {ac}}$
the anti-cuspidal part of
$\mathbf {T}_{\textrm {ac}}$
the anti-cuspidal part of
![]() $\mathbf {T}$
as in [Reference Kisin, Shin and ZhuKSZ21, Definition 1.5.4]. More precisely, if
$\mathbf {T}$
as in [Reference Kisin, Shin and ZhuKSZ21, Definition 1.5.4]. More precisely, if
![]() $\mathbf {T}_a$
denotes the largest anisotropic subtorus of
$\mathbf {T}_a$
denotes the largest anisotropic subtorus of
![]() $\mathbf {T}$
, then
$\mathbf {T}$
, then
![]() $\mathbf {T}_{\textrm {ac}}$
is the smallest subtorus of
$\mathbf {T}_{\textrm {ac}}$
is the smallest subtorus of
![]() $\mathbf {T}_a$
whose base change to
$\mathbf {T}_a$
whose base change to
![]() $\mathbb {R}$
contains the maximal split subtorus of
$\mathbb {R}$
contains the maximal split subtorus of
![]() $(\mathbf {T}_a)_{\mathbb {R}}$
.
$(\mathbf {T}_a)_{\mathbb {R}}$
.
We write
![]() ${\mathbf {G}}^c$
for the quotient
${\mathbf {G}}^c$
for the quotient
![]() ${\mathbf {G}}^c / \mathbf {Z}_{\textrm {ac}}$
, and if
${\mathbf {G}}^c / \mathbf {Z}_{\textrm {ac}}$
, and if
![]() $\mathsf {H}$
is a subgroup of
$\mathsf {H}$
is a subgroup of
![]() ${\mathbf {G}}(\mathbb {A}_f)$
, we write
${\mathbf {G}}(\mathbb {A}_f)$
, we write
![]() $\mathsf {H}^c$
for the image of
$\mathsf {H}^c$
for the image of
![]() $\mathsf {H}$
under
$\mathsf {H}$
under
![]() ${\mathbf {G}}(\mathbb {A}_f) \to {\mathbf {G}}^c(\mathbb {A}_f)$
. We also denote by
${\mathbf {G}}(\mathbb {A}_f) \to {\mathbf {G}}^c(\mathbb {A}_f)$
. We also denote by
![]() $G^c$
the base change of
$G^c$
the base change of
![]() ${\mathbf {G}}^c$
to
${\mathbf {G}}^c$
to
![]() $\mathbb {Q}_p$
. The following lemma will be used below.
$\mathbb {Q}_p$
. The following lemma will be used below.
Lemma 4.1. If
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is a morphism of Shimura data then
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1)\to (\mathbf {G},\mathbf {X})$
is a morphism of Shimura data then
![]() $\alpha (\mathbf {Z}_{1,\textrm {ac}})\subseteq \mathbf {Z}_{\textrm {ac}}$
and so
$\alpha (\mathbf {Z}_{1,\textrm {ac}})\subseteq \mathbf {Z}_{\textrm {ac}}$
and so
![]() $\alpha $
induces a map
$\alpha $
induces a map
![]() $\alpha \colon \mathbf {G}_1^c\to \mathbf {G}^c$
. Consequently, if
$\alpha \colon \mathbf {G}_1^c\to \mathbf {G}^c$
. Consequently, if
![]() $(\mathbf {G},\mathbf {X})$
is of Hodge type, then the natural maps
$(\mathbf {G},\mathbf {X})$
is of Hodge type, then the natural maps
![]() $\mathbf {G}\to \mathbf {G}^c$
and
$\mathbf {G}\to \mathbf {G}^c$
and
![]() $\mathbf {G}^{\mathrm {ab}}\to (\mathbf {G}^{\mathrm {ab}})^c$
are isomorphisms.
$\mathbf {G}^{\mathrm {ab}}\to (\mathbf {G}^{\mathrm {ab}})^c$
are isomorphisms.
Proof. The first claim is [Reference Imai, Kato and YoucisIKY24b, Lemma 4.7]. The second claim then follows from the first by embedding an arbitrary Hodge type datum
![]() $(\mathbf {G}, \mathbf {X})$
into one of Siegel type
$(\mathbf {G}, \mathbf {X})$
into one of Siegel type
![]() $(\mathbf {G}_1, \mathbf {X}_1)$
, where it can be explicitly checked that
$(\mathbf {G}_1, \mathbf {X}_1)$
, where it can be explicitly checked that
![]() $\mathbf {Z}_{1,\textrm {ac}}$
is trivial. For the claim concerning
$\mathbf {Z}_{1,\textrm {ac}}$
is trivial. For the claim concerning
![]() $\mathbf {G}^{\text {ab}}$
, we observe that the map
$\mathbf {G}^{\text {ab}}$
, we observe that the map
![]() $\delta \colon \mathbf {G}\to \mathbf {G}^{\text {ab}}$
restricts to a surjection
$\delta \colon \mathbf {G}\to \mathbf {G}^{\text {ab}}$
restricts to a surjection
![]() $\delta \colon \mathbf {Z}\to \mathbf {G}^{\text {ab}}$
(e.g., see [Reference MilneMil17, Example 19.25]). From here, it’s easy to check that
$\delta \colon \mathbf {Z}\to \mathbf {G}^{\text {ab}}$
(e.g., see [Reference MilneMil17, Example 19.25]). From here, it’s easy to check that
![]() $\delta $
surjects
$\delta $
surjects
![]() $\mathbf {Z}_{\textrm {ac}}$
onto
$\mathbf {Z}_{\textrm {ac}}$
onto
![]() $\mathbf {G}^{\textrm {ab}}_{\textrm {ac}}$
, and the claim follows.
$\mathbf {G}^{\textrm {ab}}_{\textrm {ac}}$
, and the claim follows.
We set
![]() $\mathcal{G}^c$
to be the parahoric model of
$\mathcal{G}^c$
to be the parahoric model of
![]() $\mathbf {G}$
induced by
$\mathbf {G}$
induced by
![]() $\mathcal{G}$
in the sense of §2.1. By construction, we see that
$\mathcal{G}$
in the sense of §2.1. By construction, we see that
![]() $G \to G^c$
extends to a morphism of group
$G \to G^c$
extends to a morphism of group
![]() $\mathbb {Z}_p$
-schemes
$\mathbb {Z}_p$
-schemes
![]() $\mathcal{G} \to \mathcal{G}^c$
. For a conjugacy class of cocharacters
$\mathcal{G} \to \mathcal{G}^c$
. For a conjugacy class of cocharacters ![]() of
of
![]() $G_{\overline {\mathbb {Q}}_p}$
, we denote by
$G_{\overline {\mathbb {Q}}_p}$
, we denote by ![]() the image of this conjugacy class under
the image of this conjugacy class under
![]() $G_{\overline {\mathbb {Q}}_p}\to G^c_{\overline {\mathbb {Q}}_p}$
.
$G_{\overline {\mathbb {Q}}_p}\to G^c_{\overline {\mathbb {Q}}_p}$
.
The shtuka over
 $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
.
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
.
We now recall the existence of a “universal shtuka” which lives over the Shimura variety
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
, as in [Reference Pappas and RapoportPR24, §4.1] and [Reference DanielsDan25, §4.2].
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
, as in [Reference Pappas and RapoportPR24, §4.1] and [Reference DanielsDan25, §4.2].
For a normal compact open subgroup
![]() $\mathsf {K}_p^{\prime } \subseteq \mathsf {K}_p$
, we temporarily write
$\mathsf {K}_p^{\prime } \subseteq \mathsf {K}_p$
, we temporarily write
![]() $\mathsf { K}'$
for the product
$\mathsf { K}'$
for the product
![]() $\mathsf {K}_p^{\prime }\mathsf {K}^p$
. Then the transition morphism
$\mathsf {K}_p^{\prime }\mathsf {K}^p$
. Then the transition morphism
is a finite étale Galois cover with Galois group
![]() $\mathsf {K}_p/(\mathsf {K}_p^{\prime }\mathbf {Z}(\mathbb {\mathbb {Q}})^{-}_{\mathsf {K}})$
, where
$\mathsf {K}_p/(\mathsf {K}_p^{\prime }\mathbf {Z}(\mathbb {\mathbb {Q}})^{-}_{\mathsf {K}})$
, where
![]() $\mathbf {Z}(\mathbb {\mathbb {Q}})^{-}_{\mathsf {K}}$
is the closure of
$\mathbf {Z}(\mathbb {\mathbb {Q}})^{-}_{\mathsf {K}}$
is the closure of
![]() $\mathbf {Z}(\mathbb {Q})\cap \mathsf {K}$
in
$\mathbf {Z}(\mathbb {Q})\cap \mathsf {K}$
in
![]() $\mathsf {K}$
(see [Reference Kisin, Shin and ZhuKSZ21, §1.5.8]). We consider the infinite-level Shimura variety
$\mathsf {K}$
(see [Reference Kisin, Shin and ZhuKSZ21, §1.5.8]). We consider the infinite-level Shimura variety
which exists as an E-scheme as each
![]() $\pi _{\mathsf {K}',\mathsf {K}}$
is affine (see [SP17, Tag 01YX]), and forms a
$\pi _{\mathsf {K}',\mathsf {K}}$
is affine (see [SP17, Tag 01YX]), and forms a
![]() $\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
-torsor for the pro-etale site (in the sense of [Reference Bhatt and ScholzeBS15]) on
$\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
-torsor for the pro-etale site (in the sense of [Reference Bhatt and ScholzeBS15]) on
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
.
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E$
.
The map
![]() $\mathsf {K}_p\to \mathcal{G}^c(\mathbb {Z}_p)$
factorizes through
$\mathsf {K}_p\to \mathcal{G}^c(\mathbb {Z}_p)$
factorizes through
![]() $\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
(see [Reference Kisin, Shin and ZhuKSZ21, §1.5.8]). Thus, as in [Reference DanielsDan25, §4.2] or [Reference Imai, Kato and YoucisIKY24b, §2.1.5 and §4.3], from the
$\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
(see [Reference Kisin, Shin and ZhuKSZ21, §1.5.8]). Thus, as in [Reference DanielsDan25, §4.2] or [Reference Imai, Kato and YoucisIKY24b, §2.1.5 and §4.3], from the
![]() $\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
-torsor
$\mathsf {K}_p/\mathbf {Z}(\mathbb {Q})_{\mathsf {K}}^{-}$
-torsor
one constructs a
![]() $\mathcal{G}^c(\mathbb {Z}_p)$
torsor
$\mathcal{G}^c(\mathbb {Z}_p)$
torsor
![]() $\mathbb {P}_{\mathsf {K}}$
on the pro-étale site (see [Reference ScholzeSch13]) of
$\mathbb {P}_{\mathsf {K}}$
on the pro-étale site (see [Reference ScholzeSch13]) of
![]() $\textrm {Sh}_{\mathsf {K}}({\mathbf {G}},X)^{\text {an}}_E$
.
$\textrm {Sh}_{\mathsf {K}}({\mathbf {G}},X)^{\text {an}}_E$
.
Proposition 4.2 ([Reference Pappas and RapoportPR24, Proposition 4.1.4] and [Reference DanielsDan25, Proposition 4.4]).
There exists a
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {K},E}$
over
$\mathscr {P}_{\mathsf {K},E}$
over
![]() $\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E^\lozenge \to \mathrm {Spd}(E)$
with one leg bounded by
$\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})_E^\lozenge \to \mathrm {Spd}(E)$
with one leg bounded by ![]() which is associated to
which is associated to
![]() $\mathbb {P}_{\mathsf {K}}$
in the sense of [Reference Pappas and RapoportPR24, §2.5]. Moreover, if
$\mathbb {P}_{\mathsf {K}}$
in the sense of [Reference Pappas and RapoportPR24, §2.5]. Moreover, if
![]() $\mathsf {K}'=\mathsf {K}_p{\mathsf {K}^p}'$
and g is in
$\mathsf {K}'=\mathsf {K}_p{\mathsf {K}^p}'$
and g is in
![]() $\mathbf {G}(\mathbb {A}_f^p)$
is such that
$\mathbf {G}(\mathbb {A}_f^p)$
is such that
![]() $g^{-1}\mathsf {K}^p g\subseteq {\mathsf {K}^p}'$
, there exist compatible isomorphisms
$g^{-1}\mathsf {K}^p g\subseteq {\mathsf {K}^p}'$
, there exist compatible isomorphisms
Integral local Shimura varieties
Let us define (see [Reference Scholze and WeinsteinSW20, Definition 24.1.1]), a parahoric local Shimura datum to be a triple
![]() $(\mathcal{G},b,\mu )$
where
$(\mathcal{G},b,\mu )$
where
-
⋄
 $\mathcal{G}$
is a parahoric group
$\mathcal{G}$
is a parahoric group
 $\mathbb {Z}_p$
-scheme with generic fiber G,
$\mathbb {Z}_p$
-scheme with generic fiber G, -
⋄
 is a conjugacy class of minuscule cocharacters of
is a conjugacy class of minuscule cocharacters of
 $G_{\overline {\mathbb {Q}}_p}$
,
$G_{\overline {\mathbb {Q}}_p}$
, -
⋄ and b is an element of
 $G(\breve {\mathbb {Q}}_p)$
inducing an element of
$G(\breve {\mathbb {Q}}_p)$
inducing an element of  (see [Reference Rapoport and ViehmannRV14, Definition 2.3]).
(see [Reference Rapoport and ViehmannRV14, Definition 2.3]).
The reflex field of
![]() $(\mathcal{G},b,\mu )$
, usually denoted E, is the field of definition of
$(\mathcal{G},b,\mu )$
, usually denoted E, is the field of definition of ![]() . A morphism
. A morphism ![]() of parahoric local Shimura datum is is a morphism of
of parahoric local Shimura datum is is a morphism of
![]() $\mathbb {Z}_p$
-group schemes
$\mathbb {Z}_p$
-group schemes
![]() $f\colon \mathcal{G}_1\to \mathcal{G}$
carrying
$f\colon \mathcal{G}_1\to \mathcal{G}$
carrying ![]() to
to ![]() and
and
![]() $b_1$
to b. If such a morphism exists, then
$b_1$
to b. If such a morphism exists, then
![]() $E_1\supseteq E$
. We say that f is an ad-isomorphism if
$E_1\supseteq E$
. We say that f is an ad-isomorphism if
![]() $f\colon G_1\to G$
is an ad-isomorphism.
$f\colon G_1\to G$
is an ad-isomorphism.
Given a parahoric local Shimura datum ![]() with reflex field E, we obtain a presheaf
with reflex field E, we obtain a presheaf
assigning to any perfectoid space S in characteristic p the set of isomorphism classes of tuples
![]() $(S^\sharp , \mathscr {P}, \phi _{\mathscr {P}}, i_r)$
, where:
$(S^\sharp , \mathscr {P}, \phi _{\mathscr {P}}, i_r)$
, where:
-
⋄
 $S^\sharp $
is the untilt of S over
$S^\sharp $
is the untilt of S over
 $\mathcal{O}_{\breve {E}}$
associated with
$\mathcal{O}_{\breve {E}}$
associated with
 $S \to \text {Spd}(\mathcal{O}_{\breve {E}})$
,
$S \to \text {Spd}(\mathcal{O}_{\breve {E}})$
, -
⋄
 $(\mathscr {P},\phi _{\mathscr {P}})$
is a
$(\mathscr {P},\phi _{\mathscr {P}})$
is a
 $\mathcal{G}$
-shtuka on S with one leg along
$\mathcal{G}$
-shtuka on S with one leg along
 $S^\sharp $
which is bounded by
$S^\sharp $
which is bounded by  (see [Reference Pappas and RapoportPR24, Definition 2.4.3]),
(see [Reference Pappas and RapoportPR24, Definition 2.4.3]), -
⋄ and
 $i_r$
is an isomorphism of
$i_r$
is an isomorphism of
 $\mathcal{G}$
-torsors
$\mathcal{G}$
-torsors  for large enough r, under which
for large enough r, under which
 $\phi _{\mathscr {P}}$
is identified with
$\phi _{\mathscr {P}}$
is identified with
 $b \times \textrm {Frob}_S$
(see [Reference Scholze and WeinsteinSW20, §25.1]).
$b \times \textrm {Frob}_S$
(see [Reference Scholze and WeinsteinSW20, §25.1]).
By [Reference Scholze and WeinsteinSW20, §25.1] and [Reference GleasonGle22, Proposition 2.23], the presheaf ![]() is a small v-sheaf (in the sense of [Reference ScholzeSch17, Definition 12.1]), which is called the integral local Shimura variety associated to the local Shimura datum
is a small v-sheaf (in the sense of [Reference ScholzeSch17, Definition 12.1]), which is called the integral local Shimura variety associated to the local Shimura datum ![]() .
.
If
![]() $k_E$
denotes the residue field of E, then by [Reference GleasonGle22, Proposition 2.30], we have a natural identification
$k_E$
denotes the residue field of E, then by [Reference GleasonGle22, Proposition 2.30], we have a natural identification
where ![]() denotes the affine Deligne-Lusztig variety associated to the triple
denotes the affine Deligne-Lusztig variety associated to the triple ![]() (see [Reference Pappas and RapoportPR24, Definition 3.3.1]). For any point x of
(see [Reference Pappas and RapoportPR24, Definition 3.3.1]). For any point x of ![]() we write
we write ![]() for the formal completion of
for the formal completion of ![]() at x in the sense of [Reference GleasonGle22].
at x in the sense of [Reference GleasonGle22].
The conjecture of Pappas and Rapoport
We now state the Pappas–Rapoport conjecture. For details, see [Reference Pappas and RapoportPR24, §4.2] and [Reference DanielsDan25, §4.3].
Suppose we have a normal flat
![]() $\mathcal{O}_E$
-model
$\mathcal{O}_E$
-model
![]() $\mathscr {S}_{\mathsf {K}}$
of
$\mathscr {S}_{\mathsf {K}}$
of
![]() $\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})_E$
, equipped with an extension
$\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})_E$
, equipped with an extension
![]() $\mathscr {P}_{\mathsf {K}}$
of the
$\mathscr {P}_{\mathsf {K}}$
of the
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {K},E}$
to a
$\mathscr {P}_{\mathsf {K},E}$
to a
![]() $\mathcal{G}^c$
-shtuka defined over
$\mathcal{G}^c$
-shtuka defined over
![]() $\mathscr {S}_{\mathsf {K}}^{\lozenge /}$
. Note that
$\mathscr {S}_{\mathsf {K}}^{\lozenge /}$
. Note that
![]() $\mathscr {P}_{\mathsf {K}}$
is necessarily bounded by
$\mathscr {P}_{\mathsf {K}}$
is necessarily bounded by ![]() by [Reference DanielsDan25, Lemma 2.1].
by [Reference DanielsDan25, Lemma 2.1].
For any point x of
![]() $\mathscr {S}_{\mathsf {K}}(\bar {k}_E)$
, the pullback
$\mathscr {S}_{\mathsf {K}}(\bar {k}_E)$
, the pullback
![]() $x^\ast \mathscr {P}_{\mathsf {K}}$
defines a
$x^\ast \mathscr {P}_{\mathsf {K}}$
defines a
![]() $\mathcal{G}^c$
-shtuka over
$\mathcal{G}^c$
-shtuka over
![]() $\text {Spd}(\bar {k}_E)$
. In turn, by [Reference Pappas and RapoportPR24, Example 2.4.9],
$\text {Spd}(\bar {k}_E)$
. In turn, by [Reference Pappas and RapoportPR24, Example 2.4.9],
![]() $x^\ast \mathscr {P}_{\mathsf {K}}$
determines a pair
$x^\ast \mathscr {P}_{\mathsf {K}}$
determines a pair
![]() $(\mathcal{P}_x, \phi _x)$
consisting of a
$(\mathcal{P}_x, \phi _x)$
consisting of a
![]() $\mathcal{G}^c$
-torsor
$\mathcal{G}^c$
-torsor
![]() $\mathcal{P}_x$
over
$\mathcal{P}_x$
over
![]() $\mathrm{Spec}\,(W(\bar {k}_E))$
along with an isomorphism
$\mathrm{Spec}\,(W(\bar {k}_E))$
along with an isomorphism
Here
![]() $\phi $
denotes the Frobenius homomorphism for
$\phi $
denotes the Frobenius homomorphism for
![]() $W(\bar {k}_E)$
. After choosing a trivialization of
$W(\bar {k}_E)$
. After choosing a trivialization of
![]() $\mathcal{P}_x$
, we obtain an element
$\mathcal{P}_x$
, we obtain an element
![]() $b_x$
in
$b_x$
in
![]() $G^c(\breve {\mathbb {Q}}_p)$
, and changing the trivialization will change
$G^c(\breve {\mathbb {Q}}_p)$
, and changing the trivialization will change
![]() $b_x$
to some
$b_x$
to some
![]() $\sigma $
-conjugate of
$\sigma $
-conjugate of
![]() $b_x$
. Therefore we obtain a well-defined conjugacy class
$b_x$
. Therefore we obtain a well-defined conjugacy class
![]() $[b_x]$
in
$[b_x]$
in
![]() $B(G^c)$
.
$B(G^c)$
.
Since the shtuka
![]() $\mathscr {P}_{\mathsf {K}}$
is bounded by
$\mathscr {P}_{\mathsf {K}}$
is bounded by ![]() , the same holds for
, the same holds for
![]() $(\mathcal{P}_x, \phi _x)$
, so the pair
$(\mathcal{P}_x, \phi _x)$
, so the pair
![]() $(\mathcal{P}_x,\text {id})$
determines a point
$(\mathcal{P}_x,\text {id})$
determines a point
![]() $x_0$
of
$x_0$
of ![]() . Hence
. Hence ![]() is nonempty, so by [Reference HeHe16, Theorem A], it follows that
is nonempty, so by [Reference HeHe16, Theorem A], it follows that
![]() $[b_x]$
belongs to
$[b_x]$
belongs to ![]() . Then the triple
. Then the triple ![]() defines a parahoric local Shimura datum, and we can consider the integral local Shimura variety
defines a parahoric local Shimura datum, and we can consider the integral local Shimura variety ![]() along with the base point
along with the base point
![]() $x_0$
(which makes sense by (4.3)).
$x_0$
(which makes sense by (4.3)).
Definition 4.3 ([Reference Pappas and RapoportPR24, Conjecture 4.2.2] and [Reference DanielsDan25, Conjecture 4.5]).
Consider a system
![]() $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
of normal flat
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
of normal flat
![]() $\mathcal{O}_E$
-models
$\mathcal{O}_E$
-models
![]() $\mathscr {S}_{\mathsf {K}}$
of
$\mathscr {S}_{\mathsf {K}}$
of
![]() $\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})$
for
$\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})$
for
![]() $\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
with
$\mathsf {K} = \mathsf {K}_p\mathsf {K}^p$
with
![]() $\mathsf {K}^p$
varying over all sufficiently small compact open subgroups of
$\mathsf {K}^p$
varying over all sufficiently small compact open subgroups of
![]() $\mathbf {G}(\mathbb {A}_f^p)$
.
$\mathbf {G}(\mathbb {A}_f^p)$
.
We say the system
![]() $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is an canonical integral model for
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is an canonical integral model for
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf { K}^p}$
if the following properties are satisfied.
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf { K}^p}$
if the following properties are satisfied.
-
(i) For every discrete valuation ring R of characteristic
 $(0,p)$
over
$(0,p)$
over
 $\mathcal{O}_E$
, (4.4)
$\mathcal{O}_E$
, (4.4) $$ \begin{align} \textrm{Sh}_{\mathsf{K}_p}(\mathbf{G},\mathbf{X})(R[1/p]) = \left(\varprojlim_{\mathsf{ K}^p} \mathscr{S}_{\mathsf{K}}(\mathbf{G},\mathbf{X})\right)(R). \end{align} $$
$$ \begin{align} \textrm{Sh}_{\mathsf{K}_p}(\mathbf{G},\mathbf{X})(R[1/p]) = \left(\varprojlim_{\mathsf{ K}^p} \mathscr{S}_{\mathsf{K}}(\mathbf{G},\mathbf{X})\right)(R). \end{align} $$
-
(ii) For every sufficiently small
 $\mathsf {K}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
and
$\mathsf {K}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
and
 ${\mathsf {K}'}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
, and element g of
${\mathsf {K}'}^p \subseteq {\mathbf {G}}(\mathbb {A}_f^p)$
, and element g of
 ${\mathbf {G}}(\mathbb {A}_f^p)$
with
${\mathbf {G}}(\mathbb {A}_f^p)$
with
 $g^{-1}{\mathsf {K}}^pg \subseteq \mathsf {K}^p$
, there are finite étale morphisms extending the corresponding maps on the generic fiber.
$g^{-1}{\mathsf {K}}^pg \subseteq \mathsf {K}^p$
, there are finite étale morphisms extending the corresponding maps on the generic fiber. $$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g)\colon \mathscr{S}_{\mathsf{K}}(\mathbf{G},\mathbf{X}) \to \mathscr{S}_{\mathsf{K}'}(\mathbf{G},\mathbf{X}) \end{align*} $$
$$ \begin{align*} t_{\mathsf{K},\mathsf{K}'}(g)\colon \mathscr{S}_{\mathsf{K}}(\mathbf{G},\mathbf{X}) \to \mathscr{S}_{\mathsf{K}'}(\mathbf{G},\mathbf{X}) \end{align*} $$
-
(iii) The
 $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
 $\mathscr {P}_{\mathsf {K},E}$
extends to a
$\mathscr {P}_{\mathsf {K},E}$
extends to a
 $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
 $\mathscr {P}_{\mathsf {K}}$
on
$\mathscr {P}_{\mathsf {K}}$
on
 $\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})^{\lozenge /}$
for every sufficiently small
$\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})^{\lozenge /}$
for every sufficiently small
 $\mathsf {K}^p \subseteq \mathbf {G}(\mathbb {A}_f^p)$
.
$\mathsf {K}^p \subseteq \mathbf {G}(\mathbb {A}_f^p)$
. -
(iv) Consider x in
 $\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})(\bar {k}_E)$
with corresponding element
$\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})(\bar {k}_E)$
with corresponding element
 $b_x$
of
$b_x$
of
 $G(\breve {\mathbb {Q}}_p)$
, and let
$G(\breve {\mathbb {Q}}_p)$
, and let
 $x_0$
be the natural base point in
$x_0$
be the natural base point in  . Then there is an isomorphism of v-sheaves (4.5)such that
. Then there is an isomorphism of v-sheaves (4.5)such that
 $\Theta _x^\ast (\mathscr {P}_{\mathsf {K}})$
agrees with the universal
$\Theta _x^\ast (\mathscr {P}_{\mathsf {K}})$
agrees with the universal
 $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
 $\mathscr {P}^{\textrm {univ}}$
on
$\mathscr {P}^{\textrm {univ}}$
on  .
.
We observe the following uniqueness properties concerning a system of models satisfying the Pappas–Rapoport conjecture.
Proposition 4.4 (cf. [Reference Pappas and RapoportPR24, Corollary 2.7.10 and Theorem 4.2.4]).
A canonical integral model of
![]() $\{\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
and the
$\{\textrm {Sh}_{\mathsf { K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
and the
![]() $\mathcal{G}^c$
-shtukas
$\mathcal{G}^c$
-shtukas
![]() $\mathscr {P}_{\mathsf {K}}$
on these canonical integral models, are unique up to unique isomorphism (if they exist).
$\mathscr {P}_{\mathsf {K}}$
on these canonical integral models, are unique up to unique isomorphism (if they exist).
The following is then what we refer to as the Pappas–Rapoport conjecture.
Conjecture 4.5 (Pappas-Rapoport).
For any parahoric Shimura datum
![]() $(\mathcal{G},\mathbf {G},\mathbf {X})$
, there exists a canonical integral model for
$(\mathcal{G},\mathbf {G},\mathbf {X})$
, there exists a canonical integral model for
![]() $\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
.
$\{\textrm {Sh}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
.
Conjecture 4.5 is known in the following cases, where we have elected to use our notation from §3.3 for maximal clarity.
Theorem 4.6 ([Reference Pappas and RapoportPR24, Theorem 4.5.2] and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b, Corollary 4.1.5]).
For any parahoric Shimura datum
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
of Hodge type, the system
$(\mathbf {G},\mathbf {X},\mathcal{G})$
of Hodge type, the system ![]() satisfies the conditions of the Pappas–Rapoport conjecture.
satisfies the conditions of the Pappas–Rapoport conjecture.
Remark 4.7. In [Reference Pappas and RapoportPR24], Pappas and Rapoport prove the conjecture under the stubborn technical assumption that
![]() $\mathsf {K}_p$
is a stabilizer parahoric, i.e., where
$\mathsf {K}_p$
is a stabilizer parahoric, i.e., where
![]() $\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
for a parahoric group scheme
$\mathsf {K}_p = \mathcal{G}(\mathbb {Z}_p)$
for a parahoric group scheme
![]() $\mathcal{G}$
which is also the Bruhat–Tits stabilizer group scheme of a point in the extended Bruhat–Tits building of G. This assumption frequently holds; for example every parahoric
$\mathcal{G}$
which is also the Bruhat–Tits stabilizer group scheme of a point in the extended Bruhat–Tits building of G. This assumption frequently holds; for example every parahoric
![]() $\mathbb {Z}_p$
-model of G is of this form if
$\mathbb {Z}_p$
-model of G is of this form if
![]() $\pi _1(G)_I$
is torsion free. That said, it eliminates many examples of Shimura varieties of abelian type (e.g., many cases of type
$\pi _1(G)_I$
is torsion free. That said, it eliminates many examples of Shimura varieties of abelian type (e.g., many cases of type
![]() $D^{\mathbb {H}}$
). The theorem was subsequently extended to arbitrary Shimura data of Hodge type in [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b].
$D^{\mathbb {H}}$
). The theorem was subsequently extended to arbitrary Shimura data of Hodge type in [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b].
Theorem 4.8 ([Reference DanielsDan25, Theorem A]).
If
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of toral type, then
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of toral type, then
![]() $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
satisfies the conditions of the Pappas–Rapoport conjecture.
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
satisfies the conditions of the Pappas–Rapoport conjecture.
Proof. This follows from [Reference DanielsDan25, Theorem A] along with Proposition 3.20.
Theorem 4.9 ([Reference Imai, Kato and YoucisIKY24b, Proposition 5.35]).
If
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type where
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type where
![]() $\mathcal{G}$
is reductive, then the canonical integral models
$\mathcal{G}$
is reductive, then the canonical integral models ![]() from [Reference KisinKis10] satisfy the conditions of the Pappas–Rapoport conjecture.
from [Reference KisinKis10] satisfy the conditions of the Pappas–Rapoport conjecture.
4.2 Statement of the main result and applications
We now state our main result and give some applications to the study of Kisin–Pappas–Zhou models.
Theorem 4.10. Let
![]() $p>2$
,
$p>2$
,
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura data of abelian type, and suppose there exists a well-adapted parahoric Shimura datum of Hodge type
$(\mathbf {G},\mathbf {X},\mathcal{G})$
be a parahoric Shimura data of abelian type, and suppose there exists a well-adapted parahoric Shimura datum of Hodge type
![]() $\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
such that the following conditions are satisfied:
$\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
such that the following conditions are satisfied:
-
(i) The center
 $Z(G_1)$
of
$Z(G_1)$
of
 $G_1$
is an R-smooth torus, and
$G_1$
is an R-smooth torus, and -
(ii)
 $\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective.
$\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective.
Then, the system
![]() $\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
satisfies the conditions of the Pappas–Rapoport conjecture.
$\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
satisfies the conditions of the Pappas–Rapoport conjecture.
As an immediate implication, we record the following corollary.
Corollary 4.11. Suppose that
![]() $p>2$
. Then, the Pappas–Rapoport conjecture holds for all parahoric Shimura data of abelian type.
$p>2$
. Then, the Pappas–Rapoport conjecture holds for all parahoric Shimura data of abelian type.
Proof. This follows from Theorem 4.10, once we have shown that
![]() $\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
can always be chosen such that conditions (i) and (ii) of the theorem hold.
$\mathfrak {d} = (\mathbf {G}_1, \mathbf {X}_1, \mathcal{G}_1)$
can always be chosen such that conditions (i) and (ii) of the theorem hold.
By [Reference Kisin, Pappas and ZhouKPZ24, Proposition 7.2.18], we may choose
![]() $\mathfrak {d}$
such that
$\mathfrak {d}$
such that
![]() $Z_{G_1}$
is an R-smooth torus and such that
$Z_{G_1}$
is an R-smooth torus and such that
![]() $\pi _1(G_1^{\mathrm {der}})$
is a 2-group which is trivial if
$\pi _1(G_1^{\mathrm {der}})$
is a 2-group which is trivial if
![]() $(\mathbf {G}^{\text {ad}}, \mathbf {X}^{\text {ad}})$
has no factors of type
$(\mathbf {G}^{\text {ad}}, \mathbf {X}^{\text {ad}})$
has no factors of type
![]() $D^{\mathbb {H}}$
. Thus it remains only to check that
$D^{\mathbb {H}}$
. Thus it remains only to check that
![]() $\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective when when
$\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective when when
![]() $(\mathbf {G}^{\text {ad}}, \mathbf {X}^{\text {ad}})$
has factors of type
$(\mathbf {G}^{\text {ad}}, \mathbf {X}^{\text {ad}})$
has factors of type
![]() $D^{\mathbb {H}}$
. Writing
$D^{\mathbb {H}}$
. Writing
![]() $G^{\text {ad}}$
as a product of simple groups, we may reduce to the case where
$G^{\text {ad}}$
as a product of simple groups, we may reduce to the case where
![]() $G^{\text {ad}}$
is simple and of type
$G^{\text {ad}}$
is simple and of type
![]() $D_n^{\mathbb {H}}$
for some n. By the explicit descriptions of
$D_n^{\mathbb {H}}$
for some n. By the explicit descriptions of
![]() $\pi _1(G_1^{\mathrm {der}})$
and
$\pi _1(G_1^{\mathrm {der}})$
and
![]() $G^{\text {ad}}$
given in [Reference Kisin, Pappas and ZhouKPZ24, Proof of Proposition 7.2.18] and [Reference Kisin, Pappas and ZhouKPZ24, §6.2.2], respectively, both
$G^{\text {ad}}$
given in [Reference Kisin, Pappas and ZhouKPZ24, Proof of Proposition 7.2.18] and [Reference Kisin, Pappas and ZhouKPZ24, §6.2.2], respectively, both
![]() $\pi _1(G_1^{\mathrm {der}})$
and
$\pi _1(G_1^{\mathrm {der}})$
and
![]() $\pi _1(G_1^{\text {ad}})$
are induced I-modules. As the map
$\pi _1(G_1^{\text {ad}})$
are induced I-modules. As the map
![]() $\pi _1(G_1^{\mathrm {der}}) \to \pi _1(G_1^{\textrm {ad}})$
is injective, it follows that
$\pi _1(G_1^{\mathrm {der}}) \to \pi _1(G_1^{\textrm {ad}})$
is injective, it follows that
![]() $\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective.Footnote
10
$\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective.Footnote
10
In addition, utilizing Proposition 4.4, and the previously known cases of the Pappas–Rapoport conjecture stated above, we can deduce the following omnibus independence result where, again, we are using notation from §3.3.
Corollary 4.12. Suppose that
![]() $p>2$
and
$p>2$
and
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Then, the following statements are true.
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type. Then, the following statements are true.
-
(1) The system
 $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is canonically independent of the choice of
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
is canonically independent of the choice of
 $\mathfrak {d}$
.
$\mathfrak {d}$
. -
(2) If
 $(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type, then the system
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is of Hodge type, then the system  is canonically isomorphic to the system
is canonically isomorphic to the system
 $\{\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
for any
$\{\mathscr {S}_{\mathsf {K}}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
for any
 $\mathfrak {d}$
.
$\mathfrak {d}$
. -
(3) If
 $\mathcal{G}$
is reductive then the system
$\mathcal{G}$
is reductive then the system  is canonically isomorphic to the system
is canonically isomorphic to the system
 $\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
for any
$\{\mathscr {S}^{\mathfrak {d}}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
for any
 $\mathfrak {d}$
.
$\mathfrak {d}$
.
Given this independence result, the notation
![]() $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf { K}^p}$
and
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf { K}^p}$
and
![]() $\mathscr {S}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})$
for any of the systems of models discussed in §3.3 is unambiguous.
$\mathscr {S}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})$
for any of the systems of models discussed in §3.3 is unambiguous.
Remark 4.13. One implication of Corollary 4.12 is the fact that the more naively constructed models ![]() possess a local model diagram (e.g., see (3) of [Reference Kisin, Pappas and ZhouKPZ24, Theorem 7.2.20]) even if [Reference Kisin, Pappas and ZhouKPZ24, Condition (D) of §7.1.10] does not hold. Indeed, this follows by combining [Reference Kisin, Pappas and ZhouKPZ24, Theorem 7.2.18] and (2) of Corollary 4.12.
possess a local model diagram (e.g., see (3) of [Reference Kisin, Pappas and ZhouKPZ24, Theorem 7.2.20]) even if [Reference Kisin, Pappas and ZhouKPZ24, Condition (D) of §7.1.10] does not hold. Indeed, this follows by combining [Reference Kisin, Pappas and ZhouKPZ24, Theorem 7.2.18] and (2) of Corollary 4.12.
Lastly, we observe that Theorem 4.10 implies functoriality for the systems
![]() $\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
.
$\{\mathscr {S}_{\mathsf {K}}(\mathbf {G},\mathbf {X})\}_{\mathsf {K}^p}$
.
Theorem 4.14. Suppose that
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
is a morphism of acceptable parahoric Shimura data of abelian type. Then, there exists a unique morphism
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
is a morphism of acceptable parahoric Shimura data of abelian type. Then, there exists a unique morphism
which is equivariant for the map
![]() $\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
, and whose generic fiber recovers the map
$\alpha \colon \mathbf {G}_1(\mathbb {A}_f^p)\to \mathbf {G}(\mathbb {A}_f^p)$
, and whose generic fiber recovers the map
Proof. This follows from the arguments of [Reference Pappas and RapoportPR24, Corollary 4.3.2], and [Reference Daniels, van Hoften, Kim and ZhangDvHKZ24b, Corollary 4.0.9]. We replicate the proof here for completeness.
We first observe, as in [Reference Pappas and RapoportPR24, Proof of Corollary 4.3.2], that the product
determines an integral model of
![]() $\textrm {Sh}_{\mathsf {K}_{p,1}\times \mathsf {K}_p}(\mathbf {G}_1 \times \mathbf {G}, \mathbf {X}_1\times \mathbf {X})$
which satisfies Conjecture 4.5. Then by [Reference Pappas and RapoportPR24, Theorem 4.3.1], the graph of
$\textrm {Sh}_{\mathsf {K}_{p,1}\times \mathsf {K}_p}(\mathbf {G}_1 \times \mathbf {G}, \mathbf {X}_1\times \mathbf {X})$
which satisfies Conjecture 4.5. Then by [Reference Pappas and RapoportPR24, Theorem 4.3.1], the graph of
![]() $\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1,)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
determines a unique morphism of integral models
$\alpha \colon (\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1,)\to (\mathbf {G},\mathbf {X},\mathcal{G})$
determines a unique morphism of integral models
![]() $\mathscr {S}_{\mathsf {K}_{p,1}}(\mathbf {G}_1, \mathbf {X}_1) \to \mathscr {S}"$
which extends the graph of
$\mathscr {S}_{\mathsf {K}_{p,1}}(\mathbf {G}_1, \mathbf {X}_1) \to \mathscr {S}"$
which extends the graph of
![]() $\alpha $
on the generic fiber. We obtain the desired morphism by composition with the projection
$\alpha $
on the generic fiber. We obtain the desired morphism by composition with the projection
![]() $\mathscr {S}" \to \mathscr {S}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})_{E_1}$
.
$\mathscr {S}" \to \mathscr {S}_{\mathsf { K}_p}(\mathbf {G},\mathbf {X})_{E_1}$
.
5 The proof of the main result
This final section is devoted to the proof of our main theorem (Theorem 4.10). This will require the development of multiple ancillary concepts and results that we hope will be useful in other contexts. We fix notation as at the beginning of §4.
5.1 An auxiliary Kisin–Pappas–Zhou model
A useful heuristic for Shimura data of abelian type is that they are ‘spanned’ by two (largely orthogonal) extremes: Shimura data of Hodge type and Shimura data of toral type. Finding a precise formalism to realize this heuristic, especially when their integral models are part of the picture, is somewhat subtle. That said, this was achieved at hyperspecial level by Lovering in [Reference LoveringLov17a]. The goal of this subsection is to extend this formalism to the Kisin–Pappas–Zhou models of §3.
The Lovering construction
We begin by recalling the underlying Shimura datum as defined in [Reference LoveringLov17a, §4.6]. Let us fix an extension
![]() $\mathbf {E}'$
of
$\mathbf {E}'$
of
![]() $\mathbf {E}$
. Define then the group
$\mathbf {E}$
. Define then the group
where ![]() ,
,
![]() $\delta $
is the canonical map
$\delta $
is the canonical map
![]() $\mathbf {G}\to \mathbf {G}^{\text {ab}}$
, and r is obtained as the composition
$\mathbf {G}\to \mathbf {G}^{\text {ab}}$
, and r is obtained as the composition
Here
![]() $\mu _h\colon \mathbb {G}_{m,\mathbf {E}'}\to \mathbf {G}^{\text {ab}}_{\mathbf {E}'}$
denotes the composition
$\mu _h\colon \mathbb {G}_{m,\mathbf {E}'}\to \mathbf {G}^{\text {ab}}_{\mathbf {E}'}$
denotes the composition
![]() $\delta \circ \mu $
for any element
$\delta \circ \mu $
for any element
![]() $\mu $
of
$\mu $
of ![]() , which is defined over
, which is defined over
![]() $\mathbf {E}'$
by the definition of reflex field and independent of choice since
$\mathbf {E}'$
by the definition of reflex field and independent of choice since
![]() $\mathbf {G}^{\text {ab}}_{\mathbb {C}}$
is abelian, and N denotes the natural norm map. Observe that
$\mathbf {G}^{\text {ab}}_{\mathbb {C}}$
is abelian, and N denotes the natural norm map. Observe that
![]() $\mathbf {B}_{\mathbf {E}'}^{\mathrm {der}}=\mathbf {G}^{\mathrm {der}}$
, so we have a short exact sequence
$\mathbf {B}_{\mathbf {E}'}^{\mathrm {der}}=\mathbf {G}^{\mathrm {der}}$
, so we have a short exact sequence
Furthermore, we have an exact sequence
and thus
![]() $\mathbf {B}_{\mathbf {E}'}$
is reductive (see [Reference MilneMil17, Corollary 21.53]).
$\mathbf {B}_{\mathbf {E}'}$
is reductive (see [Reference MilneMil17, Corollary 21.53]).
Let
![]() $\{\tau \}$
be the set of Archimedean places of
$\{\tau \}$
be the set of Archimedean places of
![]() $\mathbf {E}'$
, and let
$\mathbf {E}'$
, and let
![]() $\{[\tau ]\}$
denote the set of equivalence classes under the relation
$\{[\tau ]\}$
denote the set of equivalence classes under the relation
![]() $\tau \sim \overline {\tau }$
. Let
$\tau \sim \overline {\tau }$
. Let
![]() $\tau _0\colon \mathbf {E}'\to \mathbb {C}$
be the natural inclusion which defines an element
$\tau _0\colon \mathbf {E}'\to \mathbb {C}$
be the natural inclusion which defines an element
![]() $[\tau _0]$
of
$[\tau _0]$
of
![]() $\{[\tau ]\}$
. Then, we have that
$\{[\tau ]\}$
. Then, we have that
![]() $\mathbf {E}'\otimes _{\mathbb {Q}}\mathbb {R}$
is isomorphic to
$\mathbf {E}'\otimes _{\mathbb {Q}}\mathbb {R}$
is isomorphic to
![]() $\prod _{[\tau ]}\mathbf {E}^{\prime }_{[\tau ]}$
, where
$\prod _{[\tau ]}\mathbf {E}^{\prime }_{[\tau ]}$
, where
![]() $\mathbf {E}^{\prime }_{[\tau ]}$
is
$\mathbf {E}^{\prime }_{[\tau ]}$
is
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
if
$\mathbb {C}$
if
![]() $\tau $
is real or complex, respectively. We define
$\tau $
is real or complex, respectively. We define
to be the unique morphism having trivial projection
![]() $h_{\mathbf {T}_{\mathbf {E}'},[\tau ]}$
to every
$h_{\mathbf {T}_{\mathbf {E}'},[\tau ]}$
to every
![]() $[\tau ]$
not equal to
$[\tau ]$
not equal to
![]() $[\tau _0]$
, and satisfying
$[\tau _0]$
, and satisfying
 $$ \begin{align*} h_{\mathbf{T}_{\mathbf{E}'},[\tau_0]}(z)=\begin{cases}z\overline{z} & \mbox{if}\quad \tau_0\text{ is real},\\ z & \mbox{if} \quad \tau_0\text{ is complex},\end{cases} \end{align*} $$
$$ \begin{align*} h_{\mathbf{T}_{\mathbf{E}'},[\tau_0]}(z)=\begin{cases}z\overline{z} & \mbox{if}\quad \tau_0\text{ is real},\\ z & \mbox{if} \quad \tau_0\text{ is complex},\end{cases} \end{align*} $$
for z in
![]() $\mathbb {S}(\mathbb {R})=\mathbb {C}^\times $
.
$\mathbb {S}(\mathbb {R})=\mathbb {C}^\times $
.
One may show (see [Reference LoveringLov17a, Proposition 4.6.5]) that for any element h of
![]() $\mathbf {X}$
, the pair
$\mathbf {X}$
, the pair
factorizes through
![]() $(\mathbf {B}_{\mathbf {E}'})_{\mathbb {R}}$
, that the resulting
$(\mathbf {B}_{\mathbf {E}'})_{\mathbb {R}}$
, that the resulting
![]() $\mathbf {B}_{\mathbf {E}'}(\mathbb {R})$
-conjugacy class
$\mathbf {B}_{\mathbf {E}'}(\mathbb {R})$
-conjugacy class
![]() $\mathbf {Y}_{\mathbf {E}'}$
is independent of the choice of h, and that the pair
$\mathbf {Y}_{\mathbf {E}'}$
is independent of the choice of h, and that the pair
![]() $(\mathbf {B}_{\mathbf {E}'},\mathbf {Y}_{\mathbf {E}'})$
is a Shimura datum with reflex field
$(\mathbf {B}_{\mathbf {E}'},\mathbf {Y}_{\mathbf {E}'})$
is a Shimura datum with reflex field
![]() $\mathbf {E}'$
. Moreover, there is a commutative diagram of Shimura data:
$\mathbf {E}'$
. Moreover, there is a commutative diagram of Shimura data:

where
![]() $\mathbf {B}_{\mathbf {E}'}\to \mathbf {G}$
,
$\mathbf {B}_{\mathbf {E}'}\to \mathbf {G}$
,
![]() $\mathbf {B}_{\mathbf {E}'}\to \mathbf {T}_{\mathbf {E}'}$
, and
$\mathbf {B}_{\mathbf {E}'}\to \mathbf {T}_{\mathbf {E}'}$
, and
![]() $\mathbf {G}\to \mathbf {G}^{\text {ab}}$
are the natural maps, and the map
$\mathbf {G}\to \mathbf {G}^{\text {ab}}$
are the natural maps, and the map
![]() $\mathbf {T}_{\mathbf {E}'}\to \mathbf {G}^{\text {ab}}$
is the norm map. We call
$\mathbf {T}_{\mathbf {E}'}\to \mathbf {G}^{\text {ab}}$
is the norm map. We call
![]() $(\mathbf {B}_{\mathbf {E}'},\mathbf {Y}_{\mathbf {E}'})$
the Lovering construction applied to
$(\mathbf {B}_{\mathbf {E}'},\mathbf {Y}_{\mathbf {E}'})$
the Lovering construction applied to
![]() $(\mathbf {G},\mathbf {X})$
. When
$(\mathbf {G},\mathbf {X})$
. When
![]() $\mathbf {E}'=\mathbf {E}$
, we simplify
$\mathbf {E}'=\mathbf {E}$
, we simplify
![]() $\mathbf {T}_{\mathbf {E}}$
,
$\mathbf {T}_{\mathbf {E}}$
,
![]() $\mathbf {B}_{\mathbf {E}}$
, and
$\mathbf {B}_{\mathbf {E}}$
, and
![]() $\mathbf {Y}_{\mathbf {E}}$
to
$\mathbf {Y}_{\mathbf {E}}$
to
![]() $\mathbf {T}$
,
$\mathbf {T}$
,
![]() $\mathbf {B}$
, and
$\mathbf {B}$
, and
![]() $\mathbf {Y}$
, respectively.
$\mathbf {Y}$
, respectively.
We now record the following pleasant functoriality property of the Lovering construction.
Proposition 5.1 ([Reference LoveringLov17a, Lemma 4.6.6]).
Let
![]() $(\mathbf {G}_1,\mathbf {X}_1)$
be another Shimura datum and let
$(\mathbf {G}_1,\mathbf {X}_1)$
be another Shimura datum and let
![]() $\mathbf {E}'$
be a field containing the compositum
$\mathbf {E}'$
be a field containing the compositum
![]() $\mathbf {E}_1\mathbf {E}$
. Suppose that
$\mathbf {E}_1\mathbf {E}$
. Suppose that
![]() $f\colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
is an isogeny which induces an isomorphism
$f\colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
is an isogeny which induces an isomorphism ![]() . Then there exists a unique map
. Then there exists a unique map
![]() $g\colon \mathbf {B}_{1,\mathbf {E}'}\to \mathbf {B}$
filling in the following diagram
$g\colon \mathbf {B}_{1,\mathbf {E}'}\to \mathbf {B}$
filling in the following diagram

where N is the natural norm map. Moreover, g induces a morphism of Shimura data
![]() $(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})\to (\mathbf {B},\mathbf {Y})$
.
$(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})\to (\mathbf {B},\mathbf {Y})$
.
Relationship to Kisin–Pappas–Zhou models
We now explain how the Lovering construction fits into the theory of Kisin–Pappas–Zhou models.
To begin, let us fix a parahoric Shimura of Hodge type
![]() $\mathfrak {d}=(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
well-adapted to
$\mathfrak {d}=(\mathbf {G}_1,\mathbf {X}_1,\mathcal{G}_1)$
well-adapted to
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
such that
$(\mathbf {G},\mathbf {X},\mathcal{G})$
such that
![]() $Z(G_1)$
is an R-smooth torus, and let us explicitly denote by f the implicitly defined isogeny
$Z(G_1)$
is an R-smooth torus, and let us explicitly denote by f the implicitly defined isogeny
![]() $\mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
. We further set
$\mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
. We further set
![]() $\mathbf {E}'=\mathbf {E}\mathbf {E}_1$
.
$\mathbf {E}'=\mathbf {E}\mathbf {E}_1$
.
Consider the Lovering constructions
![]() $(\mathbf {B},\mathbf {Y})$
and
$(\mathbf {B},\mathbf {Y})$
and
![]() $(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})$
. For notational simplicity we shorten
$(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})$
. For notational simplicity we shorten
![]() $(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})$
to
$(\mathbf {B}_{1,\mathbf {E}'},\mathbf {Y}_{1,\mathbf {E}'})$
to
![]() $(\mathbf {B}_1',\mathbf {Y}_1')$
, and similarly for other attendant notation. Observe that both of these Shimura data are of abelian type and, in fact,
$(\mathbf {B}_1',\mathbf {Y}_1')$
, and similarly for other attendant notation. Observe that both of these Shimura data are of abelian type and, in fact,
![]() $(\mathbf {G}_1,\mathbf {X}_1)$
is an associated parahoric Shimura datum of Hodge type adapted to both. Indeed, this follows since
$(\mathbf {G}_1,\mathbf {X}_1)$
is an associated parahoric Shimura datum of Hodge type adapted to both. Indeed, this follows since
and so we may consider the isogenies
which produce the desired isomorphisms on adjoint Shimura data (cf. Proposition 2.4).
We would like to upgrade this setup to the level of parahoric Shimura data. To this end, observe that by (5.3) and Lemma 2.5 one deduces that there are natural identifications
Thus, we may associate parahoric models
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $\mathcal{B}_1'$
to our choice of parahoric models
$\mathcal{B}_1'$
to our choice of parahoric models
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $\mathcal{G}_1$
, parahoric models, respectively. In fact, it follows from Proposition 2.15
$\mathcal{G}_1$
, parahoric models, respectively. In fact, it follows from Proposition 2.15
where
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $\mathcal{T}_1'$
are the unique parahoric models of T and
$\mathcal{T}_1'$
are the unique parahoric models of T and
![]() $T_1'$
, respectively.
$T_1'$
, respectively.
Now, applying (5.2) and Proposition 5.1 one produces a diagram of Shimura data

In particular, we obtain a diagram of
![]() $\mathbf {E}'$
-schemes
$\mathbf {E}'$
-schemes

each map equivariant for the natural map of groups. Here, we write
![]() $\mathsf {L}_p=\mathcal{B}(\mathbb {Z}_p)$
and
$\mathsf {L}_p=\mathcal{B}(\mathbb {Z}_p)$
and
![]() $\mathsf {L}^{\prime }_{p,1}=\mathcal{B}_1'(\mathbb {Z}_p)$
,
$\mathsf {L}^{\prime }_{p,1}=\mathcal{B}_1'(\mathbb {Z}_p)$
,
![]() $\mathsf {M}^{\prime }_{p,1}=\mathcal{T}_1'(\mathbb {Z}_p)$
, and
$\mathsf {M}^{\prime }_{p,1}=\mathcal{T}_1'(\mathbb {Z}_p)$
, and
![]() $\mathsf {N}_{p,1}=\mathcal{G}_1^{\text {ab}}(\mathbb {Z}_p)$
. We then have the following relationship between the Lovering construction and Kisin–Pappas–Zhou models.
$\mathsf {N}_{p,1}=\mathcal{G}_1^{\text {ab}}(\mathbb {Z}_p)$
. We then have the following relationship between the Lovering construction and Kisin–Pappas–Zhou models.
Proposition 5.2. There exists a unique diagram

whose maps are equivariant for the appropriate maps of groups, and which models (5.4) pulled back to the completion of
![]() $\mathbf {E}'$
at a prime above v.
$\mathbf {E}'$
at a prime above v.
Proof. The existence of an equivariant map
modeling the map on the generic fiber follows from Proposition 3.20, while the existence of the equivariant map
modeling the map on the generic fiber follows from Proposition 3.23. To construct the equivariant maps
modeling the maps on the generic fiber, it suffices by Proposition 3.26 and Proposition 3.25 to construct a map
Because the map
![]() $\mathbf {B}^{\prime }_1\to \mathbf {G}_1\times \mathbf {T}^{\prime }_1$
is an isomorphism on derived subgroups, we see from Proposition 2.4 that it is an ad-isomorphism, and so the claim follows from Proposition 3.22. The fact that this constructed square commutes may be checked on the generic fiber, where it is true by construction.
$\mathbf {B}^{\prime }_1\to \mathbf {G}_1\times \mathbf {T}^{\prime }_1$
is an isomorphism on derived subgroups, we see from Proposition 2.4 that it is an ad-isomorphism, and so the claim follows from Proposition 3.22. The fact that this constructed square commutes may be checked on the generic fiber, where it is true by construction.
The existence of an equivariant map
follows from Proposition 3.22 as the induced map
![]() ${\mathbf {B}^{\prime }_1}^{\mathrm {der}}\to \mathbf {B}^{\mathrm {der}}$
is identified with the isogeny
${\mathbf {B}^{\prime }_1}^{\mathrm {der}}\to \mathbf {B}^{\mathrm {der}}$
is identified with the isogeny
![]() ${f\colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}}$
and so Proposition 2.4 applies. We similarly deduce the existence of a map
${f\colon \mathbf {G}_1^{\mathrm {der}}\to \mathbf {G}}$
and so Proposition 2.4 applies. We similarly deduce the existence of a map
using the fact that
![]() $\mathbf {B}^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
is an isomorphism, along with Proposition 3.22 and Proposition 2.4.
$\mathbf {B}^{\mathrm {der}}\to \mathbf {G}^{\mathrm {der}}$
is an isomorphism, along with Proposition 3.22 and Proposition 2.4.
5.2 Construction of the
 $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
In this section we establish the following theorem.
Theorem 5.3. There exists a unique
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {K}_p}$
on
$\mathscr {P}_{\mathsf {K}_p}$
on
![]() $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
bounded by
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})$
bounded by ![]() , which is compatible with the
, which is compatible with the
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-action and which models
$\mathbf {G}(\mathbb {A}_f^p)$
-action and which models
![]() $\mathscr {P}_{\mathsf {K}_p,E}$
.
$\mathscr {P}_{\mathsf {K}_p,E}$
.
By [Reference Pappas and RapoportPR24, Corollary 2.7.10], there can be at most one shtuka
![]() $\mathscr {P}_{\mathsf {K}_p}$
modeling
$\mathscr {P}_{\mathsf {K}_p}$
modeling
![]() $\mathscr {P}_{\mathsf {K}_p, E}$
. Moreover, such a shtuka is automatically bounded by
$\mathscr {P}_{\mathsf {K}_p, E}$
. Moreover, such a shtuka is automatically bounded by ![]() by [Reference DanielsDan25, Lemma 2.1]. Thus, it suffices to construct a
by [Reference DanielsDan25, Lemma 2.1]. Thus, it suffices to construct a
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {K}_p}$
which is compatible with the
$\mathscr {P}_{\mathsf {K}_p}$
which is compatible with the
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-action and which models
$\mathbf {G}(\mathbb {A}_f^p)$
-action and which models
![]() $\mathscr {P}_{\mathsf {K}_p,E}$
. In fact, it suffices to construct a model with
$\mathscr {P}_{\mathsf {K}_p,E}$
. In fact, it suffices to construct a model with
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-action of
$\mathbf {G}(\mathbb {A}_f^p)$
-action of
![]() $\mathscr {P}_{\mathsf {K}_p,E'}$
for any discrete algebraic extension
$\mathscr {P}_{\mathsf {K}_p,E'}$
for any discrete algebraic extension
![]() $E'$
of E. Indeed, by [Reference Pappas and RapoportPR24, Corollary 2.7.10] one may lift the descent datum of
$E'$
of E. Indeed, by [Reference Pappas and RapoportPR24, Corollary 2.7.10] one may lift the descent datum of
![]() $\mathscr {P}_{\mathsf {K}_p,E'}$
relative to
$\mathscr {P}_{\mathsf {K}_p,E'}$
relative to
![]() $\mathscr {P}_{\mathsf {K}_p,E}$
to an integral descent datum, which is effective by [Reference Scholze and WeinsteinSW20, Proposition 19.5.3].
$\mathscr {P}_{\mathsf {K}_p,E}$
to an integral descent datum, which is effective by [Reference Scholze and WeinsteinSW20, Proposition 19.5.3].
The proof of the existence of such a model will occupy the rest of this subsection, and will be carried out in several steps.
Step 1: Group Theory
We begin by establishing the following group-theoretic result which will be useful in our construction.
Proposition 5.4. There is a canonical identification
Proof. Let us begin by verifying that there is a canonical isomorphism
Note here that we are using Lemma 4.1 to identify
![]() $\mathbf {G}_1$
and
$\mathbf {G}_1$
and
![]() $\mathbf {G}_1^{\textrm {ab}}$
with
$\mathbf {G}_1^{\textrm {ab}}$
with
![]() $\mathbf {G}_1^c$
and
$\mathbf {G}_1^c$
and
![]() $(\mathbf {G}_1^{\textrm {ab}})^c$
, respectively.
$(\mathbf {G}_1^{\textrm {ab}})^c$
, respectively.
Observe that since
![]() $\mathbf {B}_1'\to \mathbf {G}_1\times \mathbf {T}^{\prime }_1$
is an ad-isomorphism, we may use Proposition 2.4 to deduce that
$\mathbf {B}_1'\to \mathbf {G}_1\times \mathbf {T}^{\prime }_1$
is an ad-isomorphism, we may use Proposition 2.4 to deduce that
We then employ the following simple lemma.
Lemma 5.5. Let

be a Cartesian diagram, where
![]() $\mathbf {T}_i$
, for
$\mathbf {T}_i$
, for
![]() $i=1,2,3$
, are multiplicative groups over
$i=1,2,3$
, are multiplicative groups over
![]() $\mathbb {Q}$
, and such that
$\mathbb {Q}$
, and such that
![]() $\mathbf {T}_1^\circ \to \mathbf {T}_3^\circ $
is surjective. Then,
$\mathbf {T}_1^\circ \to \mathbf {T}_3^\circ $
is surjective. Then,
Proof. This follows easily from Proposition 2.14, and the observation that for a containment
![]() $A\subseteq B$
of multiplicative groups over some field F, one has that
$A\subseteq B$
of multiplicative groups over some field F, one has that
![]() $A_a=(B_a\cap A)^\circ $
and
$A_a=(B_a\cap A)^\circ $
and
![]() $A_s=(B_s\cap A)^\circ $
, where the subscripts a and s denote the maximal anisotropic and split subtori, respectively. Namely, one applies this with
$A_s=(B_s\cap A)^\circ $
, where the subscripts a and s denote the maximal anisotropic and split subtori, respectively. Namely, one applies this with
![]() $A=\mathbf {T}$
, and
$A=\mathbf {T}$
, and
![]() $B=\mathbf {T}_1\times \mathbf {T}_2$
.
$B=\mathbf {T}_1\times \mathbf {T}_2$
.
Using this, and the fact that fiber products of groups commute with quotients, we easily deduce the existence of an isomorphism as in (5.5). Note that
![]() $\mathcal{B}_1^c$
is a parahoric group by definition. The same is true of
$\mathcal{B}_1^c$
is a parahoric group by definition. The same is true of
![]() $\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
. Indeed, by Lemma 5.6 below,
$\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
. Indeed, by Lemma 5.6 below,
![]() $G_1^{\mathrm {der}}$
is R-smooth, so since
$G_1^{\mathrm {der}}$
is R-smooth, so since
![]() $\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective, it follows from Proposition 2.11 that
$\pi _1(G_1^{\mathrm {der}})_I \to \pi _1(G_1)_I$
is injective, it follows from Proposition 2.11 that
![]() $\ker (\mathcal{G}_1 \to \mathcal{G}_1^{\text {ab}})$
is
$\ker (\mathcal{G}_1 \to \mathcal{G}_1^{\text {ab}})$
is
![]() $\mathcal{G}^{\mathrm {der}}$
. Since
$\mathcal{G}^{\mathrm {der}}$
. Since
![]() $\mathcal{G}_1^{\mathrm {der}}$
is smooth with connected fibers, it then follows from Proposition 2.15 that
$\mathcal{G}_1^{\mathrm {der}}$
is smooth with connected fibers, it then follows from Proposition 2.15 that
![]() $\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
is parahoric. To conclude, it now suffices to show that
$\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
is parahoric. To conclude, it now suffices to show that
![]() $\mathcal{B}_1^c$
and
$\mathcal{B}_1^c$
and
![]() $\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
correspond to matching points under the bijection
$\mathcal{G}_1\times _{\mathcal{G}_1^{\text {ab}}}{\mathcal{T}^{\prime }_1}^{c}$
correspond to matching points under the bijection
coming from (5.5).
We have the following commutative diagram of equivariant bijections (utilizing a combination of Lemma 2.5 and Proposition 2.15 several times)

Tracing through the definitions, we see that the claim follows as the points we consider ultimately can be induced from the same point
![]() $(x,\ast )$
in the top-right corner, where
$(x,\ast )$
in the top-right corner, where
![]() $\mathcal{G}_1=\mathcal{G}_x^\circ $
. Here we are implicitly using that the formation of the (reduced) Bruhat–Tits building commutes with products.
$\mathcal{G}_1=\mathcal{G}_x^\circ $
. Here we are implicitly using that the formation of the (reduced) Bruhat–Tits building commutes with products.
Lemma 5.6. Suppose
![]() $p>2$
, and
$p>2$
, and
![]() $(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type such that
$(\mathbf {G},\mathbf {X},\mathcal{G})$
is a parahoric Shimura datum of abelian type such that
![]() $Z(G)$
is an R-smooth torus. Then
$Z(G)$
is an R-smooth torus. Then
![]() $G^{\mathrm {der}}$
is R-smooth.
$G^{\mathrm {der}}$
is R-smooth.
Proof. Under these assumptions, it follows from [Reference Kisin, Pappas and ZhouKPZ24, Remark 3.1.5 (b)] that
![]() $G^{\textrm {ad}}$
is quasi-tame in the sense of [Reference Kisin, Pappas and ZhouKPZ24, Definition 3.1.4 (1)]. Thus the same holds for the isogenous group
$G^{\textrm {ad}}$
is quasi-tame in the sense of [Reference Kisin, Pappas and ZhouKPZ24, Definition 3.1.4 (1)]. Thus the same holds for the isogenous group
![]() $G^{\textrm {der}}$
, so
$G^{\textrm {der}}$
, so
![]() $G^{\textrm {der}}$
is R-smooth by [Reference Kisin and ZhouKZ21, Proposition 2.4.6].
$G^{\textrm {der}}$
is R-smooth by [Reference Kisin and ZhouKZ21, Proposition 2.4.6].
Step 2: Pullback and Descent to the Fiber Product
Let us now recall the commutative diagram

from Proposition 5.2, with the arrows labeled for convenience, and where the arrow e is defined to make the lower triangle commute.
Utilizing Theorem 4.6 and Theorem 4.8 there exist a
![]() $\mathbf {G}_1(\mathbb {A}_f^p)$
-equivariant
$\mathbf {G}_1(\mathbb {A}_f^p)$
-equivariant
![]() $\mathcal{G}_1$
-shtuka
$\mathcal{G}_1$
-shtuka
![]() $\mathscr {P}_{\mathsf {K}_{p,1}}$
and a
$\mathscr {P}_{\mathsf {K}_{p,1}}$
and a
![]() $\mathbf {T}^{\prime }_1(\mathbb {A}_f^p)$
-equivariant
$\mathbf {T}^{\prime }_1(\mathbb {A}_f^p)$
-equivariant
![]() ${\mathcal{T}^{\prime }_1}^c$
-shtuka
${\mathcal{T}^{\prime }_1}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
on
$\mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
on ![]() and
and
![]() ${\mathscr {S}_{\mathsf {M}^{\prime }_{p,1}}(\mathbf {T}^{\prime }_1,\{h_{\mathbf {T}^{\prime }_1}\})_{\mathcal{O}_E}}$
, respectively. We then obtain a
${\mathscr {S}_{\mathsf {M}^{\prime }_{p,1}}(\mathbf {T}^{\prime }_1,\{h_{\mathbf {T}^{\prime }_1}\})_{\mathcal{O}_E}}$
, respectively. We then obtain a
![]() $\mathcal{G}_1$
-shtuka and a
$\mathcal{G}_1$
-shtuka and a
![]() ${\mathcal{T}^{\prime }_1}^{c}$
-shtuka on
${\mathcal{T}^{\prime }_1}^{c}$
-shtuka on
![]() ${\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}_{p,1}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}}$
, given by
${\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}_{p,1}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}}$
, given by
![]() $a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
$a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
![]() $d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
, respectively.
$d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
, respectively.
We claim that
![]() $a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
$a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
![]() $d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
are both equivariant relative to
$d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
are both equivariant relative to
![]() $\mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
. Indeed, this follows from the equivariance of these maps, as for an element g of
$\mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
. Indeed, this follows from the equivariance of these maps, as for an element g of
![]() $\mathbf {B}_1'(\mathbb {A}_f^p)$
we have natural isomorphisms
$\mathbf {B}_1'(\mathbb {A}_f^p)$
we have natural isomorphisms
using the
![]() $\mathbf {G}_1(\mathbb {A}_f^p)$
-equivariance of
$\mathbf {G}_1(\mathbb {A}_f^p)$
-equivariance of
![]() $\mathscr {P}_{\mathsf {K}_{p,1}}$
, and similarly in the case of
$\mathscr {P}_{\mathsf {K}_{p,1}}$
, and similarly in the case of
![]() $d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
.
$d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
.
Our plan is now to use Corollary 2.17 to glue the shtukas
![]() $a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
$a^\ast \mathscr {P}_{\mathsf {K}_{p,1}}$
and
![]() $d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
in order to obtain a
$d^\ast \mathscr {P}_{\mathsf {M}^{\prime }_{p,1}}$
in order to obtain a
![]() $\mathcal{B}_1^{\prime c}$
-shtuka on
$\mathcal{B}_1^{\prime c}$
-shtuka on
![]() $\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}_1', \mathbf {Y}_1')_{\mathcal{O}_E}$
modeling the
$\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}_1', \mathbf {Y}_1')_{\mathcal{O}_E}$
modeling the
![]() $\mathcal{B}_1^{\prime c}$
-shtuka
$\mathcal{B}_1^{\prime c}$
-shtuka
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
living over the generic fiber
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
living over the generic fiber
![]() $\textrm {Sh}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}_1', \mathbf {Y}_1')_{E'}$
, see Proposition 4.2.
$\textrm {Sh}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}_1', \mathbf {Y}_1')_{E'}$
, see Proposition 4.2.
Lemma 5.7. Let
![]() $\delta $
be the natural map
$\delta $
be the natural map
![]() $\mathcal{G}_1\to \mathcal{G}_1^{{\mathrm {ab}}}$
, and let
$\mathcal{G}_1\to \mathcal{G}_1^{{\mathrm {ab}}}$
, and let
![]() $N\colon {\mathcal{T}^{\prime }_1}^{c}\to \mathcal{G}_1^{\mathrm {ab}}$
be the (map induced by the) norm. Then there is a
$N\colon {\mathcal{T}^{\prime }_1}^{c}\to \mathcal{G}_1^{\mathrm {ab}}$
be the (map induced by the) norm. Then there is a
![]() $\mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
-equivariant isomorphism of
$\mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
-equivariant isomorphism of
![]() $\mathcal{G}_1^{{\mathrm {ab}}}$
-torsors
$\mathcal{G}_1^{{\mathrm {ab}}}$
-torsors
Proof. To construct such an isomorphism, it suffices construct compatible isomorphisms over
![]() $\mathscr {S}_{{\mathsf {L}_{p,1}'{\mathsf {L}^{\prime }_1}^{p}}}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}$
, for each neat compact open subgroup
$\mathscr {S}_{{\mathsf {L}_{p,1}'{\mathsf {L}^{\prime }_1}^{p}}}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}$
, for each neat compact open subgroup
![]() ${\mathsf {L}^{\prime }_1}^{p}\subseteq \mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
. Furthermore, by [Reference Pappas and RapoportPR24, Corollary 2.7.10], it suffices to construct such compatible isomorphisms on
${\mathsf {L}^{\prime }_1}^{p}\subseteq \mathbf {B}^{\prime }_1(\mathbb {A}_f^p)$
. Furthermore, by [Reference Pappas and RapoportPR24, Corollary 2.7.10], it suffices to construct such compatible isomorphisms on
![]() $\textrm {Sh}_{\mathsf {L}_{p,1}'{\mathsf {L}^{\prime }_1}^{p}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_E$
.
$\textrm {Sh}_{\mathsf {L}_{p,1}'{\mathsf {L}^{\prime }_1}^{p}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_E$
.
The shtukas
![]() $\mathscr {P}_{\mathsf {K}_{p,1},E}$
and
$\mathscr {P}_{\mathsf {K}_{p,1},E}$
and
![]() $\mathscr {P}_{\mathsf {M}_{p,1}}$
are functorially constructed from the corresponding étale realization functors
$\mathscr {P}_{\mathsf {M}_{p,1}}$
are functorially constructed from the corresponding étale realization functors
![]() $\mathbb {P}_{\mathsf {K}_{p,1},E}$
and
$\mathbb {P}_{\mathsf {K}_{p,1},E}$
and
![]() $\mathbb {P}_{\mathsf {M}_{p,1}}$
, respectively, in a way compatible with pullbacks along morphisms of Shimura varieties and pushforwards along morphisms of groups. Standard compatibilities of étale realizations (c.f., [Reference Imai, Kato and YoucisIKY24b, Equation (4.3.2)]) imply that there are natural isomorphisms
$\mathbb {P}_{\mathsf {M}_{p,1}}$
, respectively, in a way compatible with pullbacks along morphisms of Shimura varieties and pushforwards along morphisms of groups. Standard compatibilities of étale realizations (c.f., [Reference Imai, Kato and YoucisIKY24b, Equation (4.3.2)]) imply that there are natural isomorphisms
from where the claim follows. From this we deduce the existence of canonical isomorphisms
where
![]() $\mathscr {P}_{\mathsf {N}_{p,1}}$
is the unique model of
$\mathscr {P}_{\mathsf {N}_{p,1}}$
is the unique model of
![]() $\mathscr {P}_{\mathsf {N}_{p,1},E}$
from Theorem 4.8. The resulting composition
$\mathscr {P}_{\mathsf {N}_{p,1},E}$
from Theorem 4.8. The resulting composition ![]() is the desired isomorphism.
is the desired isomorphism.
Proposition 5.8. There exists a
![]() $\mathcal{B}_1^{\prime c}$
-shtuka
$\mathcal{B}_1^{\prime c}$
-shtuka
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
on
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
on
![]() $\mathscr {S}_{\mathsf {L}^{\prime }_{p,1}}^{\mathfrak {d}}(\mathbf {B}_1', \mathbf {Y}_1')_{\mathcal{O}_E}$
which models
$\mathscr {S}_{\mathsf {L}^{\prime }_{p,1}}^{\mathfrak {d}}(\mathbf {B}_1', \mathbf {Y}_1')_{\mathcal{O}_E}$
which models
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
.
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
.
Proof. Using Lemma 5.7, we may apply Corollary 2.17 and Proposition 5.4 to deduce the construction of a
![]() $\mathcal{B}_1^{\prime c}$
-shtuka
$\mathcal{B}_1^{\prime c}$
-shtuka
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
on
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
on
![]() ${\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}^{\prime }_1,\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}}$
. By construction this shtuka has an equivariant action of
${\mathscr {S}^{\mathfrak {d}}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}^{\prime }_1,\mathbf {Y}^{\prime }_1)_{\mathcal{O}_E}}$
. By construction this shtuka has an equivariant action of
![]() $\mathbf {B}_1'(\mathbb {A}_f^p)$
. As in the last paragraph, to show
$\mathbf {B}_1'(\mathbb {A}_f^p)$
. As in the last paragraph, to show
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
models the
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1}}$
models the
![]() ${\mathcal{B}_1'}^c$
-shtuka
${\mathcal{B}_1'}^c$
-shtuka
![]() $\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
, it suffices to show that there is an isomorphism
$\mathscr {P}_{\mathsf {L}^{\prime }_{p,1},E}$
, it suffices to show that there is an isomorphism
Here we are applying Proposition 2.16, which makes sense when one views these local systems as torsors as in [Reference Imai, Kato and YoucisIKY24b, §2.1.1]. But, in view of Proposition 5.4 this is an elementary calculation (cf. [Reference LoveringLov17b, §3.4.4]).
Step 3: Descending to
 $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
We now show that there is a
![]() $\mathbf {G}(\mathbb {A}_f^p)$
-equivariant
$\mathbf {G}(\mathbb {A}_f^p)$
-equivariant
![]() $\mathcal{G}^c$
-shtuka on
$\mathcal{G}^c$
-shtuka on
![]() $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
which models
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
which models
![]() $\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
. As previously noted, this is sufficient to prove Theorem 5.3. Let us begin by considering the
$\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
. As previously noted, this is sufficient to prove Theorem 5.3. Let us begin by considering the
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
on
![]() $\mathscr {S}_{{\mathsf {L}^{\prime }_1}^{p}}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_{E^{\textrm {ur}}}}$
.
$\mathscr {S}_{{\mathsf {L}^{\prime }_1}^{p}}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_{E^{\textrm {ur}}}}$
.
Choose a connected component
![]() ${\mathscr {S}'}^{+}$
of
${\mathscr {S}'}^{+}$
of
![]() $\mathscr {S}_{{\mathsf {L}^{\prime }_1}^p}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_{E^{\textrm {ur}}}}$
, and let
$\mathscr {S}_{{\mathsf {L}^{\prime }_1}^p}^{\mathfrak {d}}(\mathbf {B}_1',\mathbf {Y}^{\prime }_1)_{\mathcal{O}_{E^{\textrm {ur}}}}$
, and let
![]() $\mathscr {S}^+$
be the connected component of
$\mathscr {S}^+$
be the connected component of
![]() $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
containing its image under the map
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
containing its image under the map
Set
![]() ${\mathscr {P}'}^{+}$
to be the pullback of
${\mathscr {P}'}^{+}$
to be the pullback of
![]() $\mathscr {P}'$
to
$\mathscr {P}'$
to
![]() ${\mathscr {S}'}^{+}$
.
${\mathscr {S}'}^{+}$
.
Lemma 5.9. The
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() ${\mathscr {P}'}^{+}$
descends uniquely to a
${\mathscr {P}'}^{+}$
descends uniquely to a
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}^+$
on
$\mathscr {P}^+$
on
![]() $\mathscr {S}^+$
, which models the restriction of
$\mathscr {S}^+$
, which models the restriction of
![]() $\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
to
![]() $\mathscr {S}^+_{E^{\textrm {ur}}}$
$\mathscr {S}^+_{E^{\textrm {ur}}}$
Proof. As noted in the proof of Proposition 3.22, the map
![]() ${\mathscr {S}'}^{+}\to \mathscr {S}^{+}$
is a quotient by the group
${\mathscr {S}'}^{+}\to \mathscr {S}^{+}$
is a quotient by the group
which acts through a finite quotient as in [Reference KisinKis10, §E.6]. Thus, by [Reference Scholze and WeinsteinSW20, Proposition 19.5.3], it suffices to show that there is a
![]() $\Delta $
-action on
$\Delta $
-action on
![]() ${\mathscr {P}'}^{+}$
which gives a descent datum. Arguing as in Step 2, it suffices to verify that there is a
${\mathscr {P}'}^{+}$
which gives a descent datum. Arguing as in Step 2, it suffices to verify that there is a
![]() $\Delta $
-descent datum on the
$\Delta $
-descent datum on the
![]() $\mathcal{G}^c(\mathbb {Z}_p)$
-local system
$\mathcal{G}^c(\mathbb {Z}_p)$
-local system
![]() ${\mathbb {P}'}^{+}$
on
${\mathbb {P}'}^{+}$
on
![]() ${\mathscr {S}'}^{+}_{E^{\textrm {ur}}}$
, whose definition is, mutatis mutandis, the same as that of
${\mathscr {S}'}^{+}_{E^{\textrm {ur}}}$
, whose definition is, mutatis mutandis, the same as that of
![]() ${\mathscr {P}'}^{+}$
. But, this is clear as the
${\mathscr {P}'}^{+}$
. But, this is clear as the
![]() $\mathcal{G}^c(\mathbb {Z}_p)$
-local system
$\mathcal{G}^c(\mathbb {Z}_p)$
-local system
![]() $\mathbb {P}'$
on
$\mathbb {P}'$
on
![]() $\textrm {Sh}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}^{\prime }_1,\mathbf {Y}^{\prime }_1)_{E^{\textrm {ur}}}$
is the pullback of a
$\textrm {Sh}_{\mathsf {L}^{\prime }_{p,1}}(\mathbf {B}^{\prime }_1,\mathbf {Y}^{\prime }_1)_{E^{\textrm {ur}}}$
is the pullback of a
![]() $\mathcal{G}^c(\mathbb {Z}_p)$
-local system on
$\mathcal{G}^c(\mathbb {Z}_p)$
-local system on
![]() $\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
by [Reference Imai, Kato and YoucisIKY24b, Equation (4.3.2)].
$\textrm {Sh}_{\mathsf {K}_p}(\mathbf {G},\mathbf {X})_{E^{\textrm {ur}}}$
by [Reference Imai, Kato and YoucisIKY24b, Equation (4.3.2)].
Thus we obtain a
![]() $\mathcal{G}^c$
-shtuka
$\mathcal{G}^c$
-shtuka
![]() $\mathscr {P}^+$
on
$\mathscr {P}^+$
on
![]() $\mathscr {S}^+$
. That this shtuka models the restriction of
$\mathscr {S}^+$
. That this shtuka models the restriction of
![]() $\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
to
![]() $\mathscr {S}^+_{E^{\textrm {ur}}}$
is clear by design. Indeed,
$\mathscr {S}^+_{E^{\textrm {ur}}}$
is clear by design. Indeed,
![]() $\mathscr {P}^+$
is isomorphic to the
$\mathscr {P}^+$
is isomorphic to the
![]() $\mathcal{G}^c$
-shtuka obtained as the descent of
$\mathcal{G}^c$
-shtuka obtained as the descent of
![]() ${\mathscr {P}'}^{+}$
with respect to the
${\mathscr {P}'}^{+}$
with respect to the
![]() $\Delta $
-action which, as noted before, agrees with that of the restriction to
$\Delta $
-action which, as noted before, agrees with that of the restriction to
![]() $\mathscr {S}^+_{E^{\textrm {ur}}}$
of the pullback of
$\mathscr {S}^+_{E^{\textrm {ur}}}$
of the pullback of
![]() $\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
along the map in (5.6).
$\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
along the map in (5.6).
The group
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
acts transitively on
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
acts transitively on
![]() $\pi _0([\mathscr {S}^+\times \mathscr {A}(\boldsymbol{\mathcal{G}})]/\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ )$
. Thus, for any component
$\pi _0([\mathscr {S}^+\times \mathscr {A}(\boldsymbol{\mathcal{G}})]/\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ )$
. Thus, for any component
![]() $\mathscr {T}^+$
of
$\mathscr {T}^+$
of
![]() $[\mathscr {S}^+\times \mathscr {A}(\boldsymbol{\mathcal{G}})]/\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ $
we may choose some g in
$[\mathscr {S}^+\times \mathscr {A}(\boldsymbol{\mathcal{G}})]/\mathscr {A}(\boldsymbol{\mathcal{G}}_1)^\circ $
we may choose some g in
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
such that
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
such that
We define
To see that this is canonically independent of the choice of g we again note by [Reference Pappas and RapoportPR24, Corollary 2.7.10] that it suffices to verify this on the generic fiber. There, the statement follows from the fact that
![]() $\mathscr {P}^+$
models the restriction of
$\mathscr {P}^+$
models the restriction of
![]() $\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}_p,E^{\textrm {ur}}}$
to
![]() $\mathscr {S}^+_{E^{\textrm {ur}}}$
, and the
$\mathscr {S}^+_{E^{\textrm {ur}}}$
, and the
![]() $\mathscr {A}(\boldsymbol{\mathcal{G}})$
-equivariance of
$\mathscr {A}(\boldsymbol{\mathcal{G}})$
-equivariance of
![]() $\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
. Moreover, by the same logic we see that
$\mathscr {P}_{\mathsf {K}_{p},E^{\textrm {ur}}}$
. Moreover, by the same logic we see that
![]() $\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
models the restriction of
$\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
models the restriction of
![]() $\mathscr {P}_{\mathsf {K}_{p,1},E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}_{p,1},E^{\textrm {ur}}}$
to
![]() $\mathscr {T}^+_{E^{\textrm {ur}}}$
.
$\mathscr {T}^+_{E^{\textrm {ur}}}$
.
We then define
![]() $\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {C}}$
for any connected component
$\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {C}}$
for any connected component
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
by placing
![]() $\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
on each of the
$\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
on each of the
![]() $|J|$
copies of
$|J|$
copies of
![]() $\mathscr {T}^+$
. The fact that this models the shtuka
$\mathscr {T}^+$
. The fact that this models the shtuka
![]() $\mathscr {P}_{\mathsf {K}_p,E}$
follows from the definition of the model (see Remark 3.19) and the
$\mathscr {P}_{\mathsf {K}_p,E}$
follows from the definition of the model (see Remark 3.19) and the
![]() $\mathscr {A}(\mathbf {G})$
-equivariance of
$\mathscr {A}(\mathbf {G})$
-equivariance of
![]() $\mathscr {P}_{\mathsf {K}_p,E}$
.
$\mathscr {P}_{\mathsf {K}_p,E}$
.
For each neat compact open subgroup
![]() $\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
and each connected component
$\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
and each connected component
![]() $\mathscr {T}_{\mathsf {K}^p}^+$
of
$\mathscr {T}_{\mathsf {K}^p}^+$
of
![]() $\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
we may choose any connected component
$\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
we may choose any connected component
![]() $\mathscr {T}^+$
of
$\mathscr {T}^+$
of
![]() $\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
mapping to it. The fact here that the map
$\mathscr {S}_{\mathsf {K}_p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
mapping to it. The fact here that the map
is surjective follows from Lemma 3.17.
Lemma 5.10. The shtuka
![]() $\mathscr {P}_{\mathsf {K}_p, \mathcal{O}_{E^{\textrm {ur}}}, \mathscr {T}^+}$
descends along the map
$\mathscr {P}_{\mathsf {K}_p, \mathcal{O}_{E^{\textrm {ur}}}, \mathscr {T}^+}$
descends along the map
![]() $\mathscr {T}^+ \to \mathscr {T}_{\mathsf {K}^p}^+$
to a shtuka
$\mathscr {T}^+ \to \mathscr {T}_{\mathsf {K}^p}^+$
to a shtuka
![]() $\mathscr {P}_{\mathsf { K}^p, \mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
which models the restriction of
$\mathscr {P}_{\mathsf { K}^p, \mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
which models the restriction of
![]() $\mathscr {P}_{\mathsf {K}^p, E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}^p, E^{\textrm {ur}}}$
to
![]() $\mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
.
$\mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
.
Proof. The map
![]() $\mathscr {T}^+\to \mathscr {T}^+_{\mathsf {K}^p}$
is a profinite étale cover, and thus by [Reference Scholze and WeinsteinSW20, Proposition 19.5.3] to show that
$\mathscr {T}^+\to \mathscr {T}^+_{\mathsf {K}^p}$
is a profinite étale cover, and thus by [Reference Scholze and WeinsteinSW20, Proposition 19.5.3] to show that
![]() $\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
descends along this map, it suffices to produce descent data. Again by [Reference Pappas and RapoportPR24, Corollary 2.7.10], this data can be obtained using the descent data for the restriction of
$\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
descends along this map, it suffices to produce descent data. Again by [Reference Pappas and RapoportPR24, Corollary 2.7.10], this data can be obtained using the descent data for the restriction of
![]() $\mathscr {P}_{\mathsf {K}_{p,1},E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}_{p,1},E^{\textrm {ur}}}$
to
![]() $\mathscr {T}^+_{E^{\textrm {ur}}}$
relative to the map
$\mathscr {T}^+_{E^{\textrm {ur}}}$
relative to the map
![]() $\mathscr {T}^+_{E^{\textrm {ur}}}\to \mathscr {T}^+_{\mathsf {K}^p, E^{\textrm {ur}}}$
.
$\mathscr {T}^+_{E^{\textrm {ur}}}\to \mathscr {T}^+_{\mathsf {K}^p, E^{\textrm {ur}}}$
.
It is clear by the definition of
![]() $\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
, [Reference KisinKis10, Lemma 2.2.5], and the equivariance of the map
$\mathscr {P}_{\mathsf {K}_p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+}$
, [Reference KisinKis10, Lemma 2.2.5], and the equivariance of the map
![]() $\mathscr {T}^+\to \mathscr {T}^+_{\mathsf {K}^p}$
that this descent is independent of all choices, and hence we obtain
$\mathscr {T}^+\to \mathscr {T}^+_{\mathsf {K}^p}$
that this descent is independent of all choices, and hence we obtain
![]() $\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
. We conclude by observing that
$\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
. We conclude by observing that
![]() $\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
models the restriction of
$\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}},\mathscr {T}^+_{\mathsf {K}^p}}$
models the restriction of
![]() $\mathscr {P}_{\mathsf {K}^p,E^{\textrm {ur}}}$
to
$\mathscr {P}_{\mathsf {K}^p,E^{\textrm {ur}}}$
to
![]() $\mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
since, by definition, they have the same descent data relative to the map
$\mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
since, by definition, they have the same descent data relative to the map
![]() $\mathscr {T}^+_{E^{\textrm {ur}}}\to \mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
.
$\mathscr {T}^+_{E^{\textrm {ur}}}\to \mathscr {T}^+_{\mathsf {K}^p,E^{\textrm {ur}}}$
.
Finally, we can construct the desired
![]() $\mathcal{G}^c$
-shtuka on
$\mathcal{G}^c$
-shtuka on
![]() $\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G}, \mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
.
$\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G}, \mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
.
Construction 5.11. We set
 $$ \begin{align*} \mathscr{P}_{\mathsf{K}^p,\mathcal{O}_{E^{\textrm{ur}}}}=\bigsqcup_{\mathscr{T}_{\mathsf{K}^p}^+\in\pi_0(\mathscr{S}_{\mathsf{ K}_p\mathsf{ K}^p}^{\mathfrak{d}}(\mathbf{G},\mathbf{X})_{\mathcal{O}_{E^{\textrm{ur}}}})}\mathscr{P}_{\mathsf{K}^p,\mathcal{O}_{E^{\textrm{ur}}},\mathscr{T}_{\mathsf{K}^p}^+}. \end{align*} $$
$$ \begin{align*} \mathscr{P}_{\mathsf{K}^p,\mathcal{O}_{E^{\textrm{ur}}}}=\bigsqcup_{\mathscr{T}_{\mathsf{K}^p}^+\in\pi_0(\mathscr{S}_{\mathsf{ K}_p\mathsf{ K}^p}^{\mathfrak{d}}(\mathbf{G},\mathbf{X})_{\mathcal{O}_{E^{\textrm{ur}}}})}\mathscr{P}_{\mathsf{K}^p,\mathcal{O}_{E^{\textrm{ur}}},\mathscr{T}_{\mathsf{K}^p}^+}. \end{align*} $$
More precisely, let
![]() $k_E$
denote the residue field of E. Then, as
$k_E$
denote the residue field of E. Then, as
![]() $\pi _0(\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}})$
is finite, the set of objects S of
$\pi _0(\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}})$
is finite, the set of objects S of
![]() $\mathbf {Perf}_{k_E}$
such that
$\mathbf {Perf}_{k_E}$
such that
![]() $S\to (\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}})^{\lozenge /}$
factorizes through some
$S\to (\mathscr {S}_{\mathsf {K}_p\mathsf { K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}})^{\lozenge /}$
factorizes through some
![]() $(\mathscr {T}_{\mathsf {K}^p}^+)^{\lozenge /}$
is a basis of
$(\mathscr {T}_{\mathsf {K}^p}^+)^{\lozenge /}$
is a basis of
![]() $\mathbf {Perf}_{k_E}$
, and on such an object we define the
$\mathbf {Perf}_{k_E}$
, and on such an object we define the
![]() $\mathcal{G}^c$
-shtuka over S to be that determined by the (unique) map
$\mathcal{G}^c$
-shtuka over S to be that determined by the (unique) map
![]() $S\to (\mathscr {T}_{\mathsf {K}^p}^+)^{\lozenge /}$
.
$S\to (\mathscr {T}_{\mathsf {K}^p}^+)^{\lozenge /}$
.
Proof of Theorem 5.3.
It is clear from our definition of
![]() $\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}}}$
that the collection
$\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^{\textrm {ur}}}}$
that the collection
![]() $\{\mathscr {P}_{\mathsf {K}^p, \mathcal{O}_{E^{\textrm {ur}}}}\}_{\mathsf {K}^p}$
forms a compatible family of
$\{\mathscr {P}_{\mathsf {K}^p, \mathcal{O}_{E^{\textrm {ur}}}}\}_{\mathsf {K}^p}$
forms a compatible family of
![]() $\mathcal{G}^c$
-shtukas over
$\mathcal{G}^c$
-shtukas over
![]() $\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
. Also, by design,
$\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})_{\mathcal{O}_{E^{\textrm {ur}}}}$
. Also, by design,
![]() $\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^ur}}$
models
$\mathscr {P}_{\mathsf {K}^p,\mathcal{O}_{E^ur}}$
models
![]() $\mathscr {P}_{\mathsf {K}^p,E^{\textrm {ur}}}$
since it does so on each connected component. Theorem 5.3 follows.
$\mathscr {P}_{\mathsf {K}^p,E^{\textrm {ur}}}$
since it does so on each connected component. Theorem 5.3 follows.
5.3 The completion of the proof
We are now prepared to prove Theorem 4.10. Given Theorem 3.9 and Theorem 5.3 it remains to verify the following proposition.
Proposition 5.12. For any neat compact open subgroup
![]() $\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
, and x in
$\mathsf {K}^p\subseteq \mathbf {G}(\mathbb {A}_f^p)$
, and x in
![]() $\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})(\overline {k}_E)$
, there exists an isomorphism of v-sheaves
$\mathscr {S}_{\mathsf {K}^p}^{\mathfrak {d}}(\mathbf {G},\mathbf {X})(\overline {k}_E)$
, there exists an isomorphism of v-sheaves
such that
![]() $\Theta _x^\ast (\mathscr {P}_{\mathsf {K}^p})$
is isomorphic to
$\Theta _x^\ast (\mathscr {P}_{\mathsf {K}^p})$
is isomorphic to
![]() $\mathscr {P}^{\textrm {univ}}$
, with notation as in Definition 4.3.
$\mathscr {P}^{\textrm {univ}}$
, with notation as in Definition 4.3.
The key to constructing such an isomorphism is the following result of Pappas–Rapoport.
Proposition 5.13 ([Reference Pappas and RapoportPR24, Proposition 5.3.1]).
Suppose that ![]() is an ad-isomorphism of local Shimura data, and that
is an ad-isomorphism of local Shimura data, and that
![]() $x_1$
is an element of
$x_1$
is an element of ![]() with image x in
with image x in ![]() (note that
(note that
![]() $\overline {k}_{E_1}=\overline {k}_E$
). Then the induced map
$\overline {k}_{E_1}=\overline {k}_E$
). Then the induced map
is an isomorphism, and there is an identification
Proof of Proposition 5.12.
Consider the commutative diagram

from Proposition 5.2, where each map is equivariant for the relevant group homomorphism. Choose compact open subgroups
such that
![]() $(a,e)({\mathsf {L}'}^{p}_1)\subseteq \mathsf {K}_1^{p}\times {\mathsf {M}^{\prime }_1}^{p}$
and
$(a,e)({\mathsf {L}'}^{p}_1)\subseteq \mathsf {K}_1^{p}\times {\mathsf {M}^{\prime }_1}^{p}$
and
![]() $e({\mathsf {L}'}^{p}_1)\subseteq \mathsf {K}^p$
. We then obtain the diagram
$e({\mathsf {L}'}^{p}_1)\subseteq \mathsf {K}^p$
. We then obtain the diagram

from (5.2) (excluding some terms) and Proposition 3.26.
Let us now fix a point w of
![]() $\mathscr {S}^{\mathfrak {d}}_{{\mathsf {L}^{\prime }_1}^p}(\mathbf {B}_1',\mathbf {Y}_1')(\overline {k}_E)$
. We set
$\mathscr {S}^{\mathfrak {d}}_{{\mathsf {L}^{\prime }_1}^p}(\mathbf {B}_1',\mathbf {Y}_1')(\overline {k}_E)$
. We set
and
Since the maps
are isogenies, the maps
are ad-isomorphisms by Proposition 2.4. Thus, the maps e and
![]() $(a,c)$
are finite étale by Proposition 3.22, and we obtain induced isomorphisms
$(a,c)$
are finite étale by Proposition 3.22, and we obtain induced isomorphisms
Here we use the obvious notation for the complete local rings of these Kisin–Pappas–Zhou models at these
![]() $\overline {k}_E$
-points. We also use the fact that
$\overline {k}_E$
-points. We also use the fact that
![]() $\widehat {\mathcal{O}}_z$
is isomorphic to
$\widehat {\mathcal{O}}_z$
is isomorphic to
![]() $\mathcal{O}_{\breve {E}}$
(see [Reference DanielsDan25, Lemma 4.2]) to relate the local ring of
$\mathcal{O}_{\breve {E}}$
(see [Reference DanielsDan25, Lemma 4.2]) to relate the local ring of
![]() $(y,z)$
to the tensor product of local rings.
$(y,z)$
to the tensor product of local rings.
Now, by Theorem 4.6 and Theorem 4.8 we may choose isomorphisms
such that
![]() $\Theta _y^\ast (\mathscr {P}_{\mathsf {K}^{p}_1})\simeq \mathscr {P}_y^{\textrm {univ}}$
and
$\Theta _y^\ast (\mathscr {P}_{\mathsf {K}^{p}_1})\simeq \mathscr {P}_y^{\textrm {univ}}$
and
![]() $\Theta _z^\ast (\mathscr {P}_{\mathsf {M}^{'p}_1})\simeq \mathscr {P}_z^{\textrm {univ}}$
, where have used the obvious shortenings for the local cocharacters and universal shtukas. From these, we obtain an isomorphism
$\Theta _z^\ast (\mathscr {P}_{\mathsf {M}^{'p}_1})\simeq \mathscr {P}_z^{\textrm {univ}}$
, where have used the obvious shortenings for the local cocharacters and universal shtukas. From these, we obtain an isomorphism
On the other hand, since
![]() ${B}_1^{\prime c}\to {G}_1\times {{T}^{\prime }_1}^c$
is an ad-isomorphism, we see from Proposition 5.13 that we have an induced isomorphism
${B}_1^{\prime c}\to {G}_1\times {{T}^{\prime }_1}^c$
is an ad-isomorphism, we see from Proposition 5.13 that we have an induced isomorphism
Using the fact that the formation of integral local Shimura varieties commutes with products in the obvious way, we obtain an induced isomorphism
where we are again using the fact that ![]() is a point to pass to the completions.
is a point to pass to the completions.
We may then form the map
Let us observe that by design
But, since
(as follows from Proposition 5.4), [Reference Pappas and RapoportPR22, Proposition 5.1.3] implies that the map of integral local Shimura varieties
is a closed immersion. Because the map (5.9) is given at the level of objects by the push forward of shtukas along
![]() $\mathcal{B}_1^{\prime c} \to \mathcal{G}_1 \times {\mathcal{T}^{\prime }_1}^c$
, it follows from (5.8) that
$\mathcal{B}_1^{\prime c} \to \mathcal{G}_1 \times {\mathcal{T}^{\prime }_1}^c$
, it follows from (5.8) that
![]() $\Theta _w^\ast (\mathscr {P}_{{\mathsf {L}^{\prime }_1}^p})$
is isomorphic to
$\Theta _w^\ast (\mathscr {P}_{{\mathsf {L}^{\prime }_1}^p})$
is isomorphic to
![]() $\mathscr {P}_w^{\textrm {univ}}$
.
$\mathscr {P}_w^{\textrm {univ}}$
.
On the other hand, since
![]() ${B}_1^{\prime c}\to {G}^c$
is an ad-isomorphism, we deduce from Proposition 5.13 an isomorphism
${B}_1^{\prime c}\to {G}^c$
is an ad-isomorphism, we deduce from Proposition 5.13 an isomorphism
We may then define
That
![]() $\Theta ^\ast _x(\mathscr {P}_{\mathsf {K}^p})$
is isomorphic to
$\Theta ^\ast _x(\mathscr {P}_{\mathsf {K}^p})$
is isomorphic to
![]() $\mathscr {P}^{\textrm {univ}}_x$
is easy as
$\mathscr {P}^{\textrm {univ}}_x$
is easy as
 $$ \begin{align*} \begin{aligned} \Theta^\ast_x(\mathscr{P}_{\mathsf{K}^p}) &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(e^\ast \mathscr{P}_{\mathsf{K}^p})))\\ &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(\mathscr{P}_{{\mathsf{L}^{\prime}_1}^p}\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c))\\ &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(\mathscr{P}_{{\mathsf{L}^{\prime}_1}^p})\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c)\\ &\simeq (\varepsilon^{-1})^\ast(\mathscr{P}_w^{\textrm{univ}}\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c)\\ & \simeq \mathscr{P}^{\textrm{univ}}_x. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Theta^\ast_x(\mathscr{P}_{\mathsf{K}^p}) &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(e^\ast \mathscr{P}_{\mathsf{K}^p})))\\ &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(\mathscr{P}_{{\mathsf{L}^{\prime}_1}^p}\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c))\\ &\simeq (\varepsilon^{-1})^\ast(\Theta_w^\ast(\mathscr{P}_{{\mathsf{L}^{\prime}_1}^p})\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c)\\ &\simeq (\varepsilon^{-1})^\ast(\mathscr{P}_w^{\textrm{univ}}\times^{\mathcal{B}_1^{\prime c}}\mathcal{G}^c)\\ & \simeq \mathscr{P}^{\textrm{univ}}_x. \end{aligned} \end{align*} $$
Here the first isomorphism holds by definition, the second holds by our construction of
![]() $\mathscr {P}_{\mathsf {K}^p}$
as in Step 3 of §5.2, the third holds from abstract nonsense, the fourth holds by our construction of
$\mathscr {P}_{\mathsf {K}^p}$
as in Step 3 of §5.2, the third holds from abstract nonsense, the fourth holds by our construction of
![]() $\Theta _w$
, and the final isomorphism holds from the properties of
$\Theta _w$
, and the final isomorphism holds from the properties of
![]() $\varepsilon $
stated in Proposition 5.13.
$\varepsilon $
stated in Proposition 5.13.
The proof of Theorem 4.10 now follows by combining Theorem 3.9 with Theorem 5.3 and Proposition 5.12.
Acknowledgements
The authors would like to thank David Schwein, Gopal Prasad, Pol van Hoften, George Pappas, Bogdan Zavalyov, and Rong Zhou for several useful conversations. In addition, we would like to thank Pol van Hoften for pointing several subtle points in an earlier draft of this article. Part of this work was conducted during a visit to the Hausdorff Research Institute for Mathematics, and the authors thank the Institute for their hospitality.
Competing interest
The authors have no competing interests to declare.
Financial support
Part of this work was conducted during a visit to the Hausdorff Research Institute for Mathematics, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2047/1 – 390685813. During a portion of this work, the second author was supported as a JSPS fellow by a KAKENHI Grant-in-aid (grant number 22F22323)