We prove for the first time that knot Floer homology and Khovanov homology can detect non-fibered knots and that HOMFLY homology detects infinitely many knots; these theories were previously known to detect a mere six knots, all fibered. These results rely on our main technical theorem, which gives a complete classification of genus-1 knots in the 3-sphere whose knot Floer homology in the top Alexander grading is 2-dimensional. We discuss applications of this classification to problems in Dehn surgery which are carried out in two sequels. These include a proof that $0$-surgery characterizes infinitely many knots, generalizing results of Gabai from his 1987 resolution of the Property R Conjecture.

A proof of a proposition in the published paper was erroneous. We clarify the effects in this erratum.

We consider uniformly random lozenge tilings of simply connected polygons subject to a technical assumption on their limit shape. We show that the edge statistics around any point on the arctic boundary, that is not a cusp or tangency location, converge to the Airy line ensemble. Our proof proceeds by locally comparing these edge statistics with those for a random tiling of a hexagon, which are well understood. To realize this comparison, we require a nearly optimal concentration estimate for the tiling height function, which we establish by exhibiting a certain Markov chain on the set of all tilings that preserves such concentration estimates under its dynamics.

We consider the harmonic map heat flow for maps $\mathbb {R}^{2} \to \mathbb {S}^2$. It is known that solutions to the initial value problem exhibit bubbling along a well-chosen sequence of times. We prove that every sequence of times admits a subsequence along which bubbling occurs. This is deduced as a corollary of our main theorem, which shows that the solution approaches the family of multi-bubble configurations in continuous time.

We address a core partition regularity problem in Ramsey theory by proving that every finite coloring of the positive integers contains monochromatic Pythagorean pairs (i.e., $x,y\in {\mathbb N}$ such that $x^2\pm y^2=z^2$ for some $z\in {\mathbb N}$). We also show that partitions generated by level sets of multiplicative functions taking finitely many values always contain Pythagorean triples. Our proofs combine known Gowers uniformity properties of aperiodic multiplicative functions with a novel and rather flexible approach based on concentration estimates of multiplicative functions.

Building upon the pioneering work of Merle, Raphaël, Rodnianski and Szeftel [67, 68, 69], we construct exact, smooth self-similar imploding solutions to the 3D isentropic compressible Euler equations for ideal gases for all adiabatic exponents 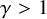$\gamma>1$. For the particular case 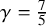$\gamma =\frac 75$ (corresponding to a diatomic gas – for example, oxygen, hydrogen, nitrogen), akin to the result [68], we show the existence of a sequence of smooth, self-similar imploding solutions. In addition, we provide simplified proofs of linear stability [67] and nonlinear stability [69], which allow us to construct asymptotically self-similar imploding solutions to the compressible Navier-Stokes equations with density independent viscosity for the case 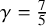$\gamma =\frac 75$. Moreover, unlike [69], the solutions constructed have density bounded away from zero and converge to a constant at infinity, representing the first example of singularity formation in such a setting.

In 2002, Fukaya [19] proposed a remarkable explanation of mirror symmetry detailing the Strominger–Yau–Zaslow (SYZ) conjecture [47] by introducing two correspondences: one between the theory of pseudo-holomorphic curves on a Calabi–Yau manifold $\check {X}$ and the multivalued Morse theory on the base $\check {B}$ of an SYZ fibration $\check {p}\colon \check {X}\to \check {B}$, and the other between deformation theory of the mirror X and the same multivalued Morse theory on $\check {B}$. In this paper, we prove a reformulation of the main conjecture in Fukaya’s second correspondence, where multivalued Morse theory on the base $\check {B}$ is replaced by tropical geometry on the Legendre dual B. In the proof, we apply techniques of asymptotic analysis developed in [7, 9] to tropicalize the pre-dgBV algebra which governs smoothing of a maximally degenerate Calabi–Yau log variety introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part $X_{\mathrm {sf}} \subset X$ allows us to extract consistent scattering diagrams from appropriate Maurer–Cartan solutions.

This article describes local normal forms of functions in noncommuting variables, up to equivalence generated by isomorphism of noncommutative Jacobi algebras, extending singularity theory in the style of Arnold’s commutative local normal forms into the noncommutative realm. This generalisation unveils many new phenomena, including an ADE classification when the Jacobi ring has dimension zero and, by taking suitable limits, a further ADE classification in dimension one. These are natural generalisations of the simple singularities and those with infinite multiplicity in Arnold’s classification. We obtain normal forms away from some exceptional Type E cases. Remarkably, these normal forms have no continuous parameters, and the key new feature is that the noncommutative world affords larger families.

This theory has a range of immediate consequences to the birational geometry of 3-folds. The normal forms of dimension zero are the analytic classification of smooth 3-fold flops, and one outcome of NC singularity theory is the first list of all Type D flopping germs, generalising Reid’s famous pagoda classification of Type A, with variants covering Type E. The normal forms of dimension one have further applications to divisorial contractions to a curve. In addition, the general techniques also give strong evidence towards new contractibility criteria for rational curves.

Inspired by work of Szymik and Wahl on the homology of Higman–Thompson groups, we establish a general connection between ample groupoids, topological full groups, algebraic K-theory spectra and infinite loop spaces, based on the construction of small permutative categories of compact open bisections. This allows us to analyse homological invariants of topological full groups in terms of homology for ample groupoids.

Applications include complete rational computations, general vanishing and acyclicity results for group homology of topological full groups as well as a proof of Matui’s AH-conjecture for all minimal, ample groupoids with comparison.

We prove the Ramanujan and Sato–Tate conjectures for Bianchi modular forms of weight at least $2$. More generally, we prove these conjectures for all regular algebraic cuspidal automorphic representations of $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$ of parallel weight, where F is any CM field. We deduce these theorems from a new potential automorphy theorem for the symmetric powers of $2$-dimensional compatible systems of Galois representations of parallel weight.

We give an affirmative answer to a long-standing conjecture of Thomassen, stating that every sufficiently highly connected graph has a k-vertex-connected orientation. We prove that a connectivity of order $O(k^2)$ suffices. As a key tool, we show that for every pair of positive integers d and t, every $(t \cdot h(d))$-connected graph contains t edge-disjoint d-rigid (in particular, d-connected) spanning subgraphs, where $h(d) = 10d(d+1)$. This also implies a positive answer to the conjecture of Kriesell that every sufficiently highly connected graph G contains a spanning tree T such that $G-E(T)$ is k-connected.

We develop a theory of quasimaps to a moduli space of sheaves M on a surface S. Under some assumptions, we prove that moduli spaces of quasimaps are proper and carry a perfect obstruction theory. Moreover, they are naturally isomorphic to moduli spaces of sheaves on threefolds $S\times C$, where C is a nodal curve. Using Zhou’s theory of entangled tails, we establish a wall-crossing formula which therefore relates the Gromov–Witten theory of M and the Donaldson–Thomas theory of $S\times C$ with relative insertions. We evaluate the wall-crossing formula for Hilbert schemes of points $S^{[n]}$, if S is a del Pezzo surface.

In a paper from 1980, Shelah constructed an uncountable group all of whose proper subgroups are countable. Assuming the continuum hypothesis, he constructed an uncountable group G that moreover admits an integer n satisfying that for every uncountable $X\subseteq G$, every element of G may be written as a group word of length n in the elements of X. The former is called a Jónsson group, and the latter is called a Shelah group.

In this paper, we construct a Shelah group on the grounds of $\textsf {{ZFC}}$ alone – that is, without assuming the continuum hypothesis. More generally, we identify a combinatorial condition (coming from the theories of negative square-bracket partition relations and strongly unbounded subadditive maps) sufficient for the construction of a Shelah group of size $\kappa $, and we prove that the condition holds true for all successors of regular cardinals (such as $\kappa =\aleph _1,\aleph _2,\aleph _3,\ldots $). This also yields the first consistent example of a Shelah group of size a limit cardinal.

A Schur multiplier is a linear map on matrices which acts on its entries by multiplication with some function, called the symbol. We consider idempotent Schur multipliers, whose symbols are indicator functions of smooth Euclidean domains. Given $1<p\neq 2<\infty $, we provide a local characterization (under some mild transversality condition) for the boundedness on Schatten p-classes of Schur idempotents in terms of a lax notion of boundary flatness. We prove in particular that all Schur idempotents are modeled on a single fundamental example: the triangular projection. As an application, we fully characterize the local $L_p$-boundedness of smooth Fourier idempotents on connected Lie groups. They are all modeled on one of three fundamental examples: the classical Hilbert transform and two new examples of Hilbert transforms that we call affine and projective. Our results in this paper are vast noncommutative generalizations of Fefferman’s celebrated ball multiplier theorem. They confirm the intuition that Schur multipliers share profound similarities with Euclidean Fourier multipliers – even in the lack of a Fourier transform connection – and complete, for Lie groups, a longstanding search of Fourier $L_p$-idempotents.

In this paper, we consider the defocusing nonlinear wave equation $-\partial _t^2u+\Delta u=|u|^{p-1}u$ in $\mathbb {R}\times \mathbb {R}^d$. Building on our companion work (Self-similar imploding solutions of the relativistic Euler equations, arXiv:2403.11471), we prove that for $d=4, p\geq 29$ and $d\geq 5, p\geq 17$, there exists a smooth complex-valued solution that blows up in finite time.