Hostname: page-component-55f67697df-jr75m Total loading time: 0 Render date: 2025-05-11T23:56:12.768Z Has data issue: false hasContentIssue false
  • English
  • Français

Research on the path planning algorithm and obstacle-crossing motion planning strategy for a cable trench inspection robot

Published online by Cambridge University Press:  10 December 2024

Linjie Dong Open the ORCID record for Linjie Dong [Opens in a new window] ,
Renfei Zhang ,
Junfei Wang ,
Jie Li ,
Shanshan Wang  and
Xingsong Wang
Linjie Dong
Affiliation:
School of Mechanical Engineering, Southeast University, Nanjing, China
Renfei Zhang
Affiliation:
School of Mechanical Engineering, Southeast University, Nanjing, China
Junfei Wang
Affiliation:
School of Mechanical Engineering, Southeast University, Nanjing, China
Jie Li
Affiliation:
College of Automation & College of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing, China
Shanshan Wang
Affiliation:
Nanjing Forestry University, Nanjing, China
Xingsong Wang*
Affiliation:
School of Mechanical Engineering, Southeast University, Nanjing, China
*
Corresponding author: Xingsong Wang; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The path planning and obstacle-crossing motion planning of cable trench inspection robots are essential for achieving automated inspection. To improve path planning efficiency and obstacle navigation in complex environments, an enhanced global path planning algorithm based on the A* algorithm has been developed, combined with an improved Dynamic Window Approach (DWA) for local path planning. For unavoidable obstacles, a specific obstacle-crossing motion planning strategy has been formulated. The enhanced A* algorithm improves efficiency and safety through adaptive neighborhood expansion and the elimination of redundant path points. The improved DWA algorithm enables real-time dynamic obstacle avoidance in local path planning. The simulation results on a 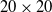$20 \times 20$ grid map indicate that the improved A* algorithm reduces the number of nodes by 58.4% and shortens the path length by 6.1% compared to the traditional A* algorithm, demonstrating significant advantages over other conventional path planning algorithms. In the simulation experiments integrating global and local path planning, the enhanced A* algorithm combined with the improved DWA algorithm reduces the path length by 3.2% on the 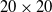$20 \times 20$ grid map compared to the integration with the traditional DWA algorithm. On the 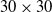$30 \times 30$ grid maps with different obstacle configurations, the path lengths are reduced by 3.5% and 3.6%, respectively. In the obstacle-crossing experiments, the robot successfully overcame obstacles of 10 cm and 20 cm in height. The proposed path planning algorithm and obstacle-crossing motion planning strategy hold substantial application potential in complex environments, offering reliable technical support for cable trench inspection robots.

Keywords

inspection robotpath planningobstacle-crossing motion planningimproved A* algorithm
Type
Research Article
Information
Robotica , First View , pp. 1 - 16
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Xie, J., Sun, T., Zhang, J., Ye, L., Fan, M. and Zhu, M., “Research on cable defect recognition technology based on image contour detection,” In: 2021, 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), IEEE (2021) pp. 387–391.Google Scholar
Khan, A. A., Malik, N., Al-Arainy, A. and Alghuwainem, S., “A review of condition monitoring of underground power cables,” In: 2012 IEEE International Conference on Condition Monitoring and Diagnosis, IEEE (2012) pp. 909–912.Google Scholar
Dong, L., Chen, N., Liang, J., Li, T., Yan, Z. and Zhang, B., “A review of indoor-orbital electrical inspection robots in substations,” Ind. Robot: Int. J. Robot. Res. Appl. 50(2), 337–352 (2022).CrossRefGoogle Scholar
Jia, Z., Tian, Y., Liu, Z. and Fan, S., “Condition assessment of the cable trench based on an intelligent inspection robot,” Front. Energy Res. 10, 860461 (2022). https://doi.org/10.3389/fenrg.2022.860461 CrossRefGoogle Scholar
Dong, L., Zhang, R., Liu, X., Li, J., Wang, X. and Mengqian, T., “High climbing and obstacle-crossing performance intelligent tracked inspection robot for cable trenches,” Ind. Robot: Int. J. Robot. Res. Appl. (2024). https://doi.org/10.1108/IR-04-2024-0184 CrossRefGoogle Scholar
Al-Araji, A. S., “Development of kinematic path-tracking controller design for real mobile robot via back-stepping slice genetic robust algorithm technique,” Arab. J. Sci. Eng. 39(12), 8825–8835 (2014).CrossRefGoogle Scholar
Ding, J., Zhou, Y., Huang, X., Song, K., Lu, S. and Wang, L., “An improved rrt* algorithm for robot path planning based on path expansion heuristic sampling,” J. Comput. Sci. 67, 101937 (2023). https://doi.org/10.1016/j.jocs.2022.101937 CrossRefGoogle Scholar
Li, J., Yang, S. X. and Xu, Z., “A survey on robot path planning using bio-inspired algorithms,” In: 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), IEEE (2019) pp. 2111–2116.Google Scholar
Ismail, A., Sheta, A. and Al-Weshah, M., “A mobile robot path planning using genetic algorithm in static environment,” J. Comput. Sci. 4(4), 341–344 (2008).Google Scholar
Tan, Y., Ouyang, J., Zhang, Z., Lao, Y. and Wen, P., “Path planning for spot welding robots based on improved ant colony algorithm,” Robotica 41(3), 926–938 (2023).CrossRefGoogle Scholar
Miao, C., Chen, G., Yan, C. and Wu, Y., “Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm,” Comput. Ind. Eng. 156, 107230 (2021). https://doi.org/10.1016/j.cie.2021.107230 CrossRefGoogle Scholar
Elhoseny, M., Tharwat, A. and Hassanien, A. E., “Bezier curve based path planning in a dynamic field using modified genetic algorithm,” J. Comput. Sci. 25, 339–350 (2018). https://doi.org/10.1016/j.jocs.2017.08.004 CrossRefGoogle Scholar
Qi, J., Yang, H. and Sun, H., “Mod-rrt*: A sampling-based algorithm for robot path planning in dynamic environment,” IEEE T. Ind. Electron. 68(8), 7244–7251 (2020).CrossRefGoogle Scholar
Elbanhawi, M. and Simic, M., “Sampling-based robot motion planning: A review,” IEEE Access 2, 56–77 (2014). https://doi.org/10.1109/access.2014.2302442 CrossRefGoogle Scholar
Duchoň, F., Babinec, A., Kajan, M., Beňo, P., Florek, M., Fico, T. and Jurišica, L., “Path planning with modified a star algorithm for a mobile robot,” Procedia Engineer. 96, 59–69 (2014). https://doi.org/10.1016/j.proeng.2014.12.098 CrossRefGoogle Scholar
Li, B., Dong, C., Chen, Q., Mu, Y., Fan, Z., Wang, Q. and Chen, X., “Path planning of mobile robots based on an improved A* algorithm,” In: Proceedings of the 2020 4th High Performance Computing and Cluster Technologies Conference & 2020 3rd International Conference on Big Data and Artificial Intelligence, (2020) pp. 49–53.Google Scholar
Razzaq Abdul Wahhab, O. A. and Al-Araji, A. S., “Path planning and control strategy design for mobile robot based on hybrid swarm optimization algorithm,” Int. J. Intell. Engineer. Sys. 14(3), 565–579 (2021).Google Scholar
Liu, S., Liu, S. and Xiao, H., “Improved gray wolf optimization algorithm integrating A* algorithm for path planning of mobile charging robots,” Robotica 42(2), 536–559 (2024).CrossRefGoogle Scholar
Wang, H., Lou, S., Jing, J., Wang, Y., Liu, W. and Liu, T., “The EBS-A* algorithm: An improved A* algorithm for path planning,” PloS one 17(2), e0263841 (2022).CrossRefGoogle Scholar
Li, C., Huang, X., Ding, J., Song, K. and Lu, S., “Global path planning based on a bidirectional alternating search A* algorithm for mobile robots,” Comput. Ind. Eng. 168, 108123 (2022). https://doi.org/10.1016/j.cie.2022.108123 CrossRefGoogle Scholar
Tang, X., Zhou, H. and Xu, T., “Obstacle avoidance path planning of 6-DOF robotic arm based on improved A* algorithm and artificial potential field method,” Robotica 42(2), 457–481 (2024).CrossRefGoogle Scholar
Y., Chen., W., Jiang., L., Yang. and Z., Luo., “Path planning based on motion constraints for mobile robot,” Comput. Integr. Manuf. Sys. 29(4), 1186 (2023).Google Scholar
Khatib, O., “Real-time obstacle avoidance for manipulators and mobile robots,” Int. J. Robot. Res. 5(1), 90–98 (1986).CrossRefGoogle Scholar
Ding, M., Zheng, X., Liu, L., Guo, J. and Guo, Y., “Collision-free path planning for cable-driven continuum robot based on improved artificial potential field,” Robotica 42(5), 1350–1367 (2024).CrossRefGoogle Scholar
Kobayashi, M. and Motoi, N., “Local path planning: Dynamic window approach with virtual manipulators considering dynamic obstacles,” IEEE Access 10, 17018–17029 (2022). https://doi.org/10.1109/ACCESS.2022.3150036 CrossRefGoogle Scholar
Sun, Y., Wang, W., Xu, M., Huang, L., Shi, K., Zou, C. and Chen, B., “Local path planning for mobile robots based on fuzzy dynamic window algorithm,” Sensors 23(19), 8260 (2023).CrossRefGoogle ScholarPubMed
Dobrevski, M. and Skočaj, D., “Dynamic adaptive dynamic window approach,” IEEE T. Robot. 40, 3068–3081 (2024). https://doi.org/10.1109/TRO.2024.3400932 CrossRefGoogle Scholar
Liu, L., Wang, X., Yang, X., Liu, H., Li, J. and Wang, P., “Path planning techniques for mobile robots: Review and prospect,” Expert Syst. Appl. 227, 120254 (2023). https://doi.org/10.1016/j.eswa.2023.120254 CrossRefGoogle Scholar
Min, C., Pan, Y., Dai, W., Kawsar, I., Li, Z. and Wang, G., “Trajectory optimization of an electric vehicle with minimum energy consumption using inverse dynamics model and servo constraints,” Mech. Mach. Theory 181, 105185 (2023). https://doi.org/10.1016/j.mechmachtheory.2022.105185 CrossRefGoogle Scholar
Yang, L., Fu, L., Li, P., Mao, J. and Guo, N., “An effective dynamic path planning approach for mobile robots based on ant colony fusion dynamic windows,” Machines 10(1), 50 (2022).CrossRefGoogle Scholar