Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-30T08:45:21.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique decipherability in the additive monoid of sets of numbers

Published online by Cambridge University Press:  13 May 2011

Aleksi Saarela
Aleksi Saarela*
Affiliation:
Department of Mathematics and Turku Centre for Computer Science TUCS, University of Turku, 20014 Turku, Finland; [email protected]
Get access

Abstract

Sets of integers form a monoid, where the product of two sets A and B is defined as the set containing a+b for all $a\in A$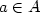 and $b\in B$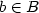. We give a characterization of when a family of finite sets is a code in this monoid, that is when the sets do not satisfy any nontrivial relation. We also extend this result for some infinite sets, including all infinite rational sets.

Keywords

Unique decipherabilityrational setsumset
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 45 , Issue 2 , April 2011 , pp. 225 - 234
Copyright
© EDP Sciences, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

J. Berstel and D. Perrin, Theory of Codes. Academic Press (1985).
Brauer, A., On a problem of partitions. Amer. J. Math. 64 (1942) 299–312. CrossRef
Ch. Choffrut and J. Karhumäki, Unique decipherability in the monoid of languages: an application of rational relations, in Proceedings of the Fourth International Computer Science Symposium in Russia (2009) 71–79.
R. Gilmer, Commutative Semigroup Rings. University of Chicago Press (1984).
J.-Y. Kao, J. Shallit and Z. Xu, The frobenius problem in a free monoid, in Proceedings of the 25th International Symposium on Theoretical Aspects of Computer Science (2008) 421–432.
Karhumäki, J. and Lisovik, L.P., The equivalence problem of finite substitutions on $ab\sp*c$, with applications. Int. J. Found. Comput. Sci. 14 (2003) 699–710. CrossRef
Kunc, M., The power of commuting with finite sets of words. Theor. Comput. Syst. 40 (2007) 521–551. CrossRef
D. Perrin, Codes conjugués. Inform. Control. 20 (1972) 222–231.
J.L. Ramírez Alfonsín, The Diophantine Frobenius Problem. Oxford University Press (2005).